Регулирование частот в ЭЭС на основе аппроксимации возмущений

«Московский физико-технический институт (национальный исследовательский университет)», 2019

вибрации лопастей генераторов с последующим их разрушением. Вследствие этого автоматика электростанции отключает энергоблоки с данными турбинами от сети, что приводит к нехватке мощности и каскадным отключениям. Восстановление работы ЭЭС в случае отключения является крайне ресурсозатратным процессом.

Регулирование частоты направлено на постоянное поддержание баланса мощности, а также частоты в номинальном значении. На данный момент оно осуществляется при помощи изменения генерации электростанций и состоит из двух частей: первичного и вторичного регулирования.

Первичное регулирование осуществляется с целью ограничения максимальных отклонений частоты от номинального значения. Изначально первичное регулирование осуществлялось при помощи центробежного (пропорционального) регулятора, на сегодняшний день регулирование осуществляется автоматикой. Тем не менее первичное регулирование по-прежнему осуществляется при помощи пропорционального регулятора [1].

Вторичное регулирование направленно на приведение частоты ЭЭС к номинальному значению. Оно представлено интегральным регулятором, направленным на сведение к нулю ошибки регулирования, равной отклонению значения частоты от номинальной.

Изменение частоты при возникновении дисбаланса мощности не происходит мгновенно. Частота в крупных ЭЭС пропорциональна частоте вращения турбин и синхронных генераторов электростанции, которые обладают большой инерцией, в силу чего изменение их скорости, а следовательно, и частоты, занимает 5-10 секунд [3]. Электростанции использующие возобновляемые источники электроэнергии (ветрогенераторы и солнечные батареи), обладают низкой или нулевой инерцией. Вследствие этого поведение частоты в ЭЭС с высоким процентом возобновляемых источников становится крайне непостоянным, и существующая схема регулирования не способна стабилизировать частоту в таких ЭЭС, что приводит к искусственному ограничению мощности, производимой возобновляемыми источниками электроэнергии (например, в 2016 году в Ирландии усредненное количество доступной, но не произведенной ветрогенераторами электроэнергии составило 227 GW, что составляет 2.7% от установленной мощности [4]).

Первичное и вторичное регулирования для работы используют только замеры частоты, тем не менее на шинах ЭЭС также производится замер электрической мощности, поступающей в шину и покидающей ее. В данной работе замеры электрической мощности вместе с частотой используются для получения приближенного значения дисбаланса мощности в сети, на основе которого производится регулирование частоты.

Регулирование частоты осуществляется изменением положения регуляционных клапанов турбины, тем самым изменяя количество энергоносителя, поступающего в турбину, и количество механической мощности, поступающей на генератор. В результате изменения механической мощности происходит изменение частоты в ЭЭС. В силу динамических процессов, происходящих в турбине, изменение механической мощности турбины происходит с некоторым запаздыванием после изменения положения регуляционных клапанов. Поэтому скорость работы существующего реагирования, полагающегося только на показания частоты, ограниченны из-за опасности возникновения положительной обратной связи.

Управление, представленное в данной работе, состоит из двух частей. Сначала производится аппроксимация возмущения, приведшего к изменению частоты в системе, далее производится корректировка значения управления с целью устранения изменения частоты. В силу того, что возмущение в сети не зависит от значения частоты, скорость работы регулирования ограничена только качеством аппроксимации возмущения в ЭЭС. Данный подход, как показывают численные эксперименты, позволяет уменьшить как максимальные отклонения частоты в сети, так и увеличить скорость их затухания. Схожий подход был использован в работе [6], в которой предполагалось, что все параметры системы известны. В данной работе рассматривается ситуация, когда параметры турбины известны с некоторой, возможно, значительной, погрешностью.

Различные подходы к регулированию частоты представлены в работах [7-9]. Но модель ЭЭС, используемая в данных работах, содержит либо модель турбины первого порядка, либо не содержит модели турбины, что может привести к неустойчивости системы, что было показано в [10]

• 2.    Математическая модель

ЭЭС задана связным орграфом Г = (N,E), г де N — множество шин (узлов), |N | = п Считается, что шина определяется ее индексом. Множество E — множество линий (ребер), |E| = q. Считается, что сеть состоит только из генераторных шин. Данное условие достигается при помощи редукции Крона [5]. Динамика ЭЭС описывается следующей системой алгебро-дифференциальных уравнений [1]:

Ө- =ш-, г Е N,(1а)

m-ш.- = - d-ш- - pt + p™ + т-, г Е N,(lb)

p-j -b-j (Ө- tj), г3 Е E,(^)

pi = 52 pij - 52 pji,г Е N, jvijeE       j:jieE t?p? = -рД + v-, г Е N,(le)

ti V i = - v- + u-(t), г Е N.(If)

Здесь переменные (неизвестные) системы:

• •    Ө - — угол сдвига, фазы на шипе г, г Е N.

• •    ш- — отклонение частоты от нос шпального 'значения на шипе г, г Е N.

• •    p - электрическая мощность, поступающая в сети из шипы г, г Е N.

• •    P ij — переток активной мопщостіi на лшше. соедпиятощей узлы г н j. Если p -j >  0. переток направлен из узла г в j, если p -j <  0, переток направлен из узла j в г, ij Е E.

• •    p™ — механическая мощность, подаваемая турбиной на генератор г, г Е N.

• •    V - — положение регуляциииных клапанов турбины г, г Е N.

Параметры (константы) системы:

• •    m - >  0 — инерционная копстаігта. генератора, на. нише г, г Е N.

• •    d - >  0 — константа. демпфирования синхронной машины на. шипе г, г Е N.

• •    т-, г Е N — суммы нагрузок и неизвестных дисбалансов мощности,

• •    b -j >  0 — парамотр липни ij. обратный се реактивной проводимости ij Е E.

• •    Р Д >  0 — временная константа, характеризующая динамику энергоносителя в турбинах на. шипе г, г Е N.

• •    t^ >  0 — временная константа, характеризующая время отклика регуляционных клапанов турбин на сигналы управления на шине г, г Е N.

Сигналы управления n-(t), г Е N являются непрерывными функциями. Уравнения имеют следующие значения:

• •    (1а.) — уравнения зависимости углов сдвига, от частоты,

• •    (1Ь) — уравнения классической модели генератора,

• •    (1с) — уравнения линеаризованных перетоков активной мощности,

• •    (1е) — уравнения, описывающие динамику турбин,

• •    (If) уравнения, описывающие динамику впускных клапанов.

Согласно [2] система (1) всегда имеет решение. Для удобства далее она сведена к системе дифференциальных уравнений, представленных в матричном виде.

Дифференцирование обеих частей уравнения (1с) дает

P ij - b ij (Ө і — Ө j ),                                            (2)

переменные ө , выражаются из (la):

^p ij    ^b ij ^{( w} *   ^w j ),

и переменные Ө і исключаются из системы. Электрические мощности р? в (lb) выражаются из (Id), что дает следующую систему дифференциалвнвіх уравнений:

Mw - — Dw — Cp + рт + г, w(0) — 0,(4а)

р -BCтw, р(0) - р0 - BCтӨ0,(4Ь)

Ттрт - — рт + в, рт(0) - рт0,(4с)

Т"в - — в + и, в(0) - в0.(4d)

Здесь используется векторное представление переменных: Ө - (Өі,...Ө_п )^т, w - (w1,..., ш_п)^т, р - (р1,...,р_д )^т, здесь и везде далее переменные р^ перенумерованы в лексикографическом порядке, поэтому имеют один индекс р*. Для удобства обозначений перенумерованные переменные обозначаются той же буквой, что и исходные, р^т - (рт,... ,р т ) в - (ві,... , в_п), и - (иі,... , и_п) и матричное представление параметров: М - diag(m1, ..., т_п), D - diag(d_i, ..., d_n) г - (г1 ,..., г_п ), B - diag(b1, ... ,b_q ), здесь параметры b ij также перенумерованы в лексикографическом порядке, Т^т - diag(tm,..., ^^т)> Т ^ - diag(t^,... ,t ^ ). Матрица C — матрица инцидентности графа Г. Необходимо отметить, что при введенных обозначениях р^е - Ср. Для данной системы верны следующие утверждения.

Лемма 1. Пусть u(t) = и*, и* G R”, тогда система (4) имеет миомеество стационарних точек (w* ,р*, (р^т)*,в* следующего вида:

*   Е j E N ^(u j ^{— r} j ) .   _

w* -            ----, г G N, jEN dj

р* G {р : Ср - —Dw* + и* + г}, р^т* - и*, в* - и*.

Доказательство. Стационарная точка системы (4) при u(t) = и* задается следующей системой уравнений:

0 - — Dw* — Ср* + (р^т)* + г,                          (ба)

0-BC Т w*,(6b)

0- — (рт)* + в*,(6с)

0 - — в* + и*.(6d)

Из уравнений (6с), (6d) следует (р^т)* - в* - и*. Матрица C является матрицей инцидентности, следовательно, 1 ^тCp - 0, где 1 — вектор, состоящий из единиц. Из (6а)

£ d,w- -£((рт)- + г*)ЖТ(и- + г,).(7)

jEN         i E N               i E N

Из уравнения (6Ь) имеем С^Тш* = 0, что в силу связности графа равносильно утверждению ш* = ш*, г, у Е N. Как следствие: ш* = ^ygybb^-)), г е N.

Лемма 2. Пусть вектор-функция u(t) является непрерывной и сходится к и* Е Rⁿ при t ^ то. Тогда система (4) является асимптоптически устойчивой по 'переменным ш. р^т. v и устойчива по р.

Доказательство. Пусть ш*,р*, (р^т)*, v* — некоторая стационарная точка системы (4) при и = и*. Тогда из леммы 1т = Вш* + Ср* — и*. Введем следутощую замену: Аш = ш — ш*. Ар = р — р*, Ар^т = р^т — (р^т)*, Av = v — v*. Тогда система (4) эквивалентна системе

М Аш = — ВАш — С Ар + Арт,(8а)

Ар =ВСТ Аш,(8b)

ТтАрт = — Арт + Av,(8с)

Ту Ай = — Av + (u(t) — и*).(8d)

Рассмотрим следующую функцию Ляпунова для однородной системы, соответствующей (8):

V(Аш, Ар, Ар^т, Av) = 1 (Аш^ТМАш + Ар^ТВ^-1Ар + (Ар^т)^ТТ^ Ар^т + Av^ТТ^ Av) . (9)

Ее производная имеет вид

!/(Аш, Ар, Ар^т, Av) = Аш^ТМАш + Ар^ТВ^-1Ар + (Ар^т)^ТТ^ Ар^т + Av^ТТ^AV =

= —Аш^ТВАш — Аш^ТС Ар + Ар^ТС ^Т Аш — (Ар^т)^Т Ар^т + (Ар^т)^Т Av — Av^T Av =   ₍₁₀₎

= —АшТВАш — |(Арт)Т Арт — |AvТ Av — |(Арт — Av)Т (Арт — Av).

Функция V(Аш, Ар, Ар^т, Av) является положительно определенной по совокупности переменных, а функция V(Аш, Ар, Ар^т, Av) — отрицательно определенной, следовательно, [11] система является устойчивой. Более того, V(Аш, Ар, Ар^т, Av) является отрицательно определенной по переменным Аш, Ар^т , Av, неоднородность u(t) — и* стремится к нулю при t ^ то, следовательно, [12] система (8) является асимптотически устойчивой по переменным Аш, Ар^т, Av. а система (4) асіімптотіічсскп устойчива по ш,р^т,v.

Лемма 3. Пусти u(t) — непрерывная еектор-функция при t > 0 такая, что u(t) ^ и* при t ^ то, где и* Е R” — некоторое решение уравнения

1^Т (и + т)=0, Т Е Rⁿ.                              (11)

Тогда система (1) сходится к следующей стационарной точке:

ш* = 0,

р* Е{р:Ср = и* + т},                               (12)

р^т* = и*, v* = и*.

Доказательство. Устойчивость системы была доказана в лемме 2. Уравнения (12) получаются после подстановки решения уравнения (11) в (6).

• 3.    Постановка задачи

Пусть

/ (и) = |иТ^и,                                 (13)

стоимость генерации, где и Е R” и W >- 0 - диагональная матрица. Определим множества Uo и U # следующим образом.

Определение 1. Множество   U q состоит из непрерывных вектор-функций

^(t) = (ді(t),..., дп(і))т таких, что

• 1)    lim_tMro д(і) = с для некоторого с Е Rⁿ;

• 2)    lim_tM^ w(t) = 0, г де w(t) — решение системы (4) при u(t) = /z(t).

Определение 2. Множество U # имеет вид

U # = {u# : u# = lim u(t) для некоторого u Е Uq}.                (14)

t M^

Необходимо найти оптимальное управление, которое определяется следующим образом:

Определение 3. Оптимальным называется управление u(t) такое, что

• 1)    ^{u Е} Uq :

• 2)    u# = arg min {/(u#) : u# Е U#}. г,те u# = lim_tM^ u(t).

Состояние, к которому приходит система при оптимальном управлении, будем называть оптимальным состоянием. Задача заключается в восстановлении частоты, а следовательно, и баланса мощности в системе с минимальными затратами. Сложность заключается в невозможности замера значений вектора возмущений г временных констант турбины и регуляционных клапанов, а также замеров механической мощности. Замеры частоты w(t) и электрической мощности p^e(t) производятся на каждой шине ЭЭС, стоимости Wi определяются системным оператором и известны. Инерции турбин М определяется ее известной массой, демпфирование D аппроксимируется для каждой турбины [1].

Существующее регулирование имеет следующий вид:

u_i (t) = u{ (t) + u¹/ (t), г Е N,

где первичное регулирование u{(t) и вторичное регулирование u ^ ¹ (t) задаются следующими формулами соответственно:

u{(t) = — K - ^ i (t), г Е N,                                    (16)

u1/ (t) = W -1у, г Е N, у = — / t Е ш к о-ж П     k E N

(17а) (17b)

Здесь K¹ >  0 и K¹¹ >  0 — константы pегулирования, у — вспомогательная функция. Введем в рассмотрение следующую вспомогательную задачу:

■ 1

(18a)

min -u Wu, u 2

1 ^T (u + г) = 0.                                    (18b)

Пусть u# — решение этой задачи. Тогда если в системе (4) u(t) ^ u#, то, согласно лемме 3, система (4) сходится к оптимальному состоянию. Данная задача является сильно выпуклой и ее единственное решение задается стационарной точкой функции Лагранжа. Функция Лагранжа:

L(u, А) = |u^TWu + Al ^T (u + г).                         (19)

Соответствующая стационарная точка определяется системой линейных уравнений:

___       ~

(20а)

(20b)

Wu + 1A = 0, что эквивалентно системе u = W-11 А,

(21а)

1 ^т (W -11^А + г) = 0.

(21b)

Решение этой системы дает

u# =

—W -11

1 ^т г

1 ^т w -11.

Если положить u(t) = u#, то система (4) сходится к оптимальному состоянию. Проблема заключается в том, что для вычисления u# необходимо знать значение вектора г, что невозможно на практике. Более того, как правило, известными считаются только частоты ш, электрические мощности ре, а также параметры М и D. Тем не менее из уравнения (4а) имеем г + рт = Мш + Dш + ре,

где ре = Ср. Значение механической мощности рт, как и матриц временных констант Тт и Т33 неизвестно, поэтому используется вспомогательная переменная рт, задаваемая уравнением

Tp^m(t) = /*

—р^т(т ) + u(t )dT, Т = diag(ti, ...,t _n ) >- 0,

где t i — положительные постоянные коэффициенты, выбор которых описан в следующем параграфе. На основе (24) выводится аппроксимация вектора возмущений:

г = Мш + D6 + р^е — р^т.

Аппроксимацию в представленном виде использовать невозможно в силу того, что значения ш неизвестны. Поэтому применяется следующий подход. В уравнении (21b) производится замена г на 7, а само уравнение заменяется на интегральное уравнение следующего вида:

A(t) = У —1^т (W 11А(т) + г(т ))dT =

= [ —1^т (W '1А(т) — D6(t ) — р^е(т )+ р^т(т )) dT + 1^тМш. 0

Таким образом, управление задается следующей системой алгебро-интегральных уравнений:

u¹¹¹ = W ^{- 1}1А,

(27а)

A(t) = / —1^т (W 11А(т) — Du(t ) — р^е(т )+ р^т (т )) dT + 1^тМш, 0

Tр^m(t) = Г —р^т(т) + u(t )dT.

(27b)

(27с)

Здесь обозначение u¹¹¹ используется для того, чтобы отличать первичное и вторичное регулирования от представленного здесь.

4. Доказательство применимости системы регулирования

Докажем теперь, что система (4), (27) является асимптотически устойчивой и управление u удовлетворяет постановке задаче. Функция Г(t) представима в следующем виде:

г (t) = г + р^т — р^т .

Таким образом, система (27) зависит только от уравнений (4с) и (4d), и для доказательства асимптотической устойчивости u(t) достаточно доказать асимптотическую устойчивость

системы (27), (4с) и (4d). Данная система содержит интегральные и

дифференциальные

уравнения. Для удобства сведем все к дифференциальной системе:

•

А =

—

1 ^T (W ^-11А + т + р^т

—

рт),

(29а)

і)т

—

(Т ^т)-!_р^т ₊ (_Т^т)

¹ г,

(29b)

•

Г =

—

(Т^V ) ^{- 1}г + (Т^V)

1W ^{- 1}1А,

(29с)

рт

~

~

—

Т-1р + Т

1W ^{- 1}1А.

(29d)

В матричном виде система представима следующим образом:

х = Ах + R,

где

(

А

\

х =

рт

г

, А =

—

1 ^TW ^-11

—

1T

1T

—

V

■рт

/

V

(Т^V ) ^{- 1}W ^-11

:t^{- 1} w ^-1і

Для этой

системы имеет

Лемма 4. Пусть

(Т т)

(Т т)

—

(Т^v ) ^{- 1}

—

:г-1

место следующий результат.

t_i >  шт^т, t - }.

Тогда система (30) асимптотически устойчива.

Доказательство. Рассмотрим характеристическое

Согласно формуле дополнения Шура

det(A — Iq) = Р1 (q)P2(q),

где

—

(Т т)

—

Iq

(Т т)

P1(q) = det

—

(Т^v ) ^{- 1}

—

Iq

/

,

R =

уравнения

~

—Т

—

Iq

/ —1 ^T _т

V

/

.

для матрицы А.

= П( iEN х

—

₊ ^{т t} i

—

q) (—I—q) (—

~

t i

—

А.

Таким образом, для того, чтобы P1(q) = 0, необходимо q < 0. Второй определитель задается

формулой

P2(q) = det

—

1 ^TW

1

—

q

—

—

—

(—х

T

1Т)

(Т т)

—

(—х

Т

) ( —((Т^т)

—

—

Iq

—

= det

(Т т)

(Т^v ) ^{- 1}

= det

N ¹

—

Iq

W ^-11

—Т ^{- 1}

—

Iq

W ^{- 1}

(Т V ) ^{- 1}      =

Д :г-1

X

(

W ^-11 (Т^- )

(

—

—

1 ^TW

1

—

q—

(Т т)-1( — (Т т)

) +К

~

—Т

—

Iq) ^{- 1}(—(Т ^V)

—

—

—

((Т^- )

—

pq)

N ¹

)

X

Iq^^W ^-11 =

^—q ⁺ ^W i

\      iEN \

—

—

^tT T ^{tV (} / ^ ⁺ q^{)(  +} q) ⁺ ^^{( 1 +} q)

ъ                ъ                         ^v^

.

Для удобства обозначим у! = ^, у2 = ^, у3 = К Тогда Z                     Z

где	Р2(у) = det [ -у + ^шг д г (п,у!,у2,уг!) ) ,                        (36) \       геіч д г (п,уг! ,у2 ,у З ) = —1 — ді(п,уг! ,у2 )+ д2г(іі,угз )>                         (З") дНфут ,у2 )=/» , !/2i , v д^Оп/Уз )= г! .                 4^) (у ! + п)(у2+ п)              угз + п

Пусть у = а + j Р. Рассмотрим условия, при которых a >  0 является решением Пру) = 0. Получим условия, при которых действительная часть дртыр,у2,Уз ) положительна. Рассмотрим сначала д^Чу! ,у2 ).

7,г иЧА -         у!у2(у!у2 + (у! + у2)а + а2 — Р2) (дг (у,у!,у2))    ((у!)2 + 2у!а + а2 +Р2)((у2)2 + 2у2а + а2 + Р2),             ' где №(•) — вещественная часть комплексного числа. Обозначим

һ(п) = у ! у 2 (у ! у 2 + (у! + у2)а + а2 — Р2),                         (40) д(у) = ((у!)2 + 2у!а + а2+ Р2)((у2)2 + 2у2а + а2+ З2).               (41)

Отметим, что д(у) > 0 для любого у G C, и һ(у) 6 0 тогда и только тогда, когда Р G Ху = {Р | Р > у\у2}. Следовательно, К(д|(у, у|,уг2)) 6 0 тогда и только тогда, когда Р G Ху и минимум №(дг!(у,у!, у2)) достигается на множестве Ху. Но на этом множестве arg min һ(у) = 0,(42)

а>0

И arg min д(у) = 0.(43)

a >0

Так как һ(у) 6 0 11 д(у) > 0. получаем argmin ^(д1 (у,уі,у2)) = 0.(44)

а>0

Рассмотрим теперь функцию д2(у, у3):

Nti )) = ттДІ^-р^Ргм,™)

(у3 )2 + 2у3а + а2 + Р2

применяя аналогичные рассуждения, получаем argmaxa>o ^(д2(п,уз)) = 0. Таким образом, argmax №(дг(у,у! ,у2,угг)) = 0.(46)

а>0

Следовательно, для вычисления максимума функции дг(у,у!, у2, у З ) можно полагать у = jp. Положим у3 = у ^ , k G {1, 2} и рассмотрим производную функции ^(д г (у, у!, у2 , у3 )):

д^(д г (jP,У1 ,у2,у3 )) ₌ у к (у! + у2 )((у ! ) ² (у 2 )² - Р⁴) дР               ((у!)² + Р²)²((у2)² + Р²)² .

Стационарными точками являются точки Р1 = л /у!у2 и Р2 = —л /у!у^. При этом г г

Жд_г №,у Х ,у 2 ,у З )) = ^(д г №,у\,у2 ,у З )) = — у^р^ < 0.          (48)

Учитывая, что lim^-^ S(gг(з3 ))   lim _; ._х S(gг(з3,У^гl , у2 , у3 )) = -1, получаем, что

^(9г(д,у\,уЧ-Фз )) < 0 при а > 0и у3 Е {уІ,у^г₂ }.

Покажем теперь, что для любого у3 такого, что 0 < у3 < max{y1 ,у2 }, неравенство

S(g_г("П^і,у^г₂ ,у З )) < 0 сохраняется. Ранее было показано, что

S(gг (ч,у1, у2,у3)) 6 s(g_г (33,у1, у2,у3)).                           (49)

Если 3 = 0, то №(д_г(0, у\ ,у₂, у3 )) = —1. Если 3 = 0, то рассмотрим следующую производную:

ӘS(gг (зЗ,у\,у2 ,у3 )) = д ^(д²(з3,у^г₃ )) =     2у3 3 ²

ду3                   ду3          ((у3 )² + 3 ² )²

Следовательно, функция S(gг(3,У1, у2, у З )) монотонно возрастает по у3, и S(gг(ч, у 1 , у 2 , у З )) < 0 Для 0 <  у З < тах{у1, у2}. Возвращаясь к полиному Р₂. получаем. что при 3 >  тіп{Д ,3 } іі а > 0 верно

s(уw, 1—1--,. \,, ---- +    ¹ И <0

. 3         «^ < г ™ ⁺ ч)( г - ⁺ ч) Л г ; ⁺ ч)

Таким образом, уравнение Р2(ч) = 0 имеет решение только при а <  0, это означает, что все действительные части собственных чисел матрицы А отрицательны и система (30) асимптотически устойчива.

Следствие 1. Система (27) задает сходягцуюся вектор-функцию n(t) такую, что система (4) сходится к оптимальному состоянию.

В силу асимптотической устойчивости система (4) имеет единственное решение, которое совпадает с решением оптимизационной задачи (18).

• 5.    Численный эксперимент

• 6.    Заключение

Для проведения численных экспериментов использовалась ЭЭС Новой Англии [3], состоящая из десяти генераторов. На первой генераторной шине происходит потеря мощности, равная 100 МВт. Предполагается, что стоимость генерации на всех шинах одинакова, таким образом, каждый генератор должен увеличить свою мощность на 10 МВт для приведения системы к оптимальному состоянию. Рассматривается три вида регулирования: (1) традиционное регулирование, состоящее из первичного и вторичного, (2) регулирование, представленное в этой работе, (3) регулирование, представленное в этой работе, вместе с первичным. На рис. 1 представлены значения управления на первом генераторе для всех трех случаев, на рис. 2 представлены соответствующие значения частоты. Как можно видеть, использование регулирования и¹¹¹ обеспечивает высокую скорость сходимости, но при этом сохраняя максимальное отклонение частоты на том же уровне, что и при традиционном регулировании. Численные эксперименты показывают, что максимальное отклонение частоты можно уменьшить при использовании разработанной схемы регулирования вместе с первичным регулированием. Как видно на рис. 2, максимальное отклонение частоты уменьшается примерно на 0.1 Гц при использовании комбинации и¹ +и^ИІ.

В представленной работе рассматривается новый подход к регулированию частоты, основанный на оценке возмущений в ЭЭС. Основным преимуществом данной схемы регулирования является значительное уменьшение времени, необходимого на восстановление частоты в ЭЭС после возникновения возмущения. При этом разработанное регулирование не требует установки какого-либо дополнительного оборудования для получения необходимой информации о состоянии ЭЭС.

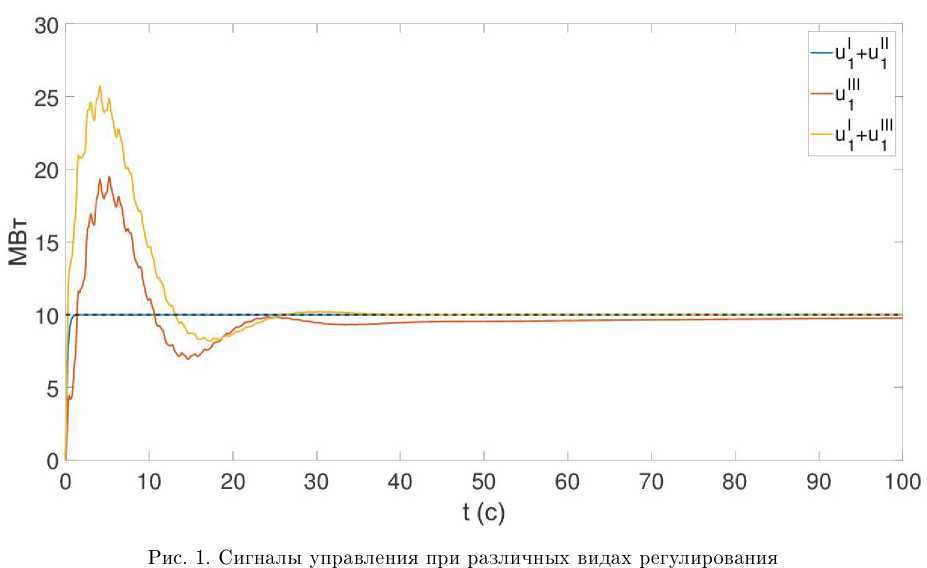
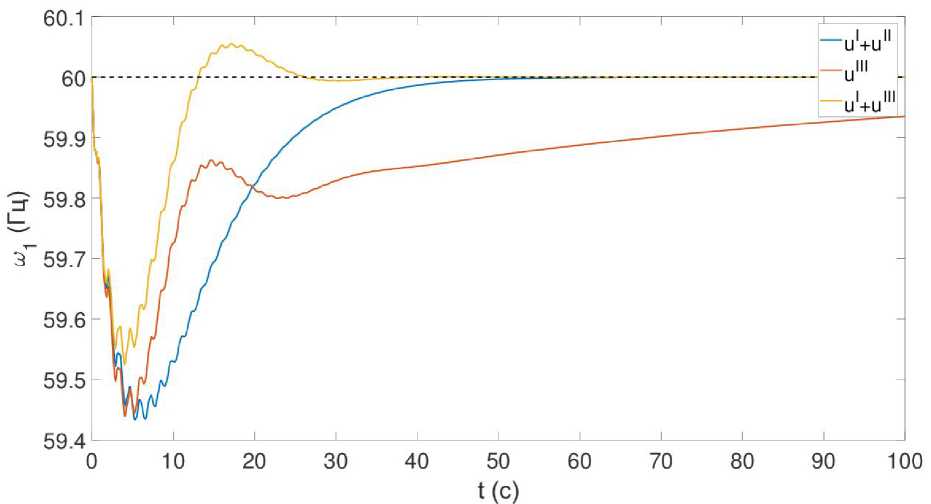
Рис. 2. Частоты в ЭЭС при различных видах регулирования