Регулирование координат электромеханической системы прокатного стана на основе наблюдателя упругого момента

Разработка системы автоматического регулирования координат на основе наблюдателя упругого момента двухмассовой электромеханической системы не является новой задачей. В публикациях [1–3] отмечается, что эта задача изначально решалась для электроприводов прокатных станов. Большие инерции двигателя, валков и длинный вал создают упругую систему. В динамических режимах скорость двигателя отличается от скорости нагрузки, и вал испытывает большой крутящий момент.

Характеристика объекта исследований

В научных публикациях [4–7] подчеркивается, что ограничение динамического момента явля- ется актуальной проблемой для электроприводов клетей толстолистовых и широкополосных станов. Это связано с тем, что их электромеханические системы работают с ударным приложением нагрузки в момент захвата металла валками. Вследствие этого возникают усталостные разрушения, приводящие к поломкам механических соединений. Как показал опыт эксплуатации стана 5000 ПАО «ММК», наименее долговечным механическим узлом является шпиндель. Поломка шпиндельных соединений приводит к длительным простоям стана и значительным затратам на устранение последствий.

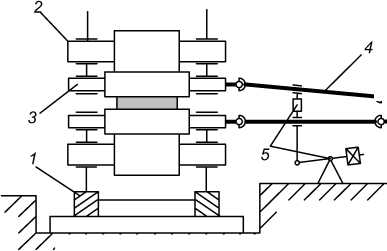
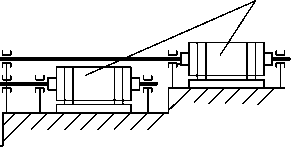
Кинематическая схема горизонтальной клети стана 5000 представлена на рис. 1а. Рабочие валки

ф

////////////

а)

б)

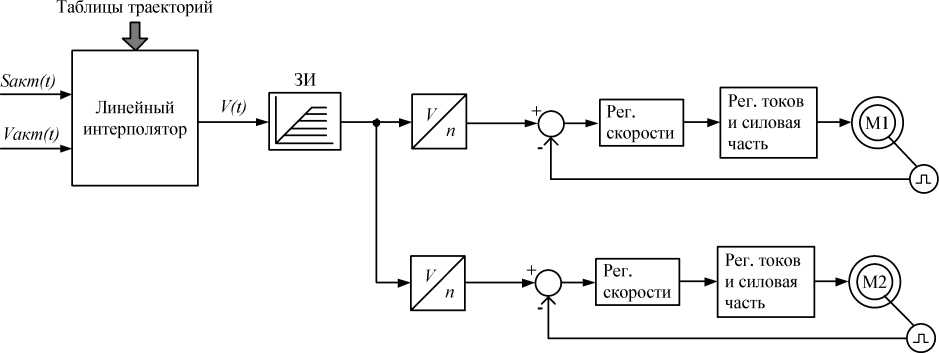
Рис. 1. Кинематическая схема горизонтальной клети (а) и структурная схема системы управления приводами стана 5000 (б): 1 – станина; 2, 3 – опорные и рабочие валки; 4 – выдвижные шпиндели; 5 – уравновешивающее устройство; 6 – электродвигатели

приводятся во вращение через шпиндели выдвижного типа. Линии главных электроприводов (главные линии) представляют собой двухмассовые электромеханические системы с упругими связями и угловыми зазорами в соединениях [8]. Соединение шпинделя с рабочим валком и ротором двигателя осуществляется с помощью головок специальной конструкции [9].

Структурная схема системы управления приводами верхнего и нижнего валков приведена на рис. 1б [10]. Электроприводы выполнены индивидуальными на основе синхронных двигателей с частотным регулированием скорости.

Ударное приложение нагрузки

Данный динамический режим возникает в момент захвата металла валками и сопровождается увеличением момента двигателя и упругого момента на шпинделе. Исследования показали, что при прокатке листов из труднодеформируемых марок стали возникают динамические нагрузки, превышающие установившийся момент прокатки в два и более раза. Как правило, это приводит к выходу электропривода на ограничение по моменту, размыканию контура регулирования скорости и возникновению затухающих колебаний.

На рис. 2 представлены осциллограммы ли- нейной скорости и момента двигателя нижнего валка и упругого момента шпинделя, подтверждающие этот вывод. Они зафиксированы при захвате металла (в момент t1) в режиме ускорения, т. е. при предварительно замкнутых зазорах. В течение длительного интервала времени (t2 – t3) момент двигателя находится на ограничении, электропривод становится неуправляемым по скорости. Упругий момент шпинделя имеет колебательный характер, его амплитудное значение МВmax достигает 6300 кН∙м и практически в 1,5 раза превышает момент ограничения (МДВmax = 4200 кН∙м или 240 % номинального). Колебания демпфируются медленно, так как разомкнут регулятор скорости. Механическая часть при этом представляется двумя интеграторами, по сути, это колебательное звено.

Приведенные осциллограммы подтверждают актуальность разработки способов управления, обеспечивающих снижение моментов двигателя и шпинделя в режиме захвата. Перспективным направлением является разработка замкнутой системы прямого регулирования скорости валка на основе наблюдателя, обеспечивающего восстановление скорости и упругого момента шпинделя по непрерывно измеряемым параметрам электропривода.

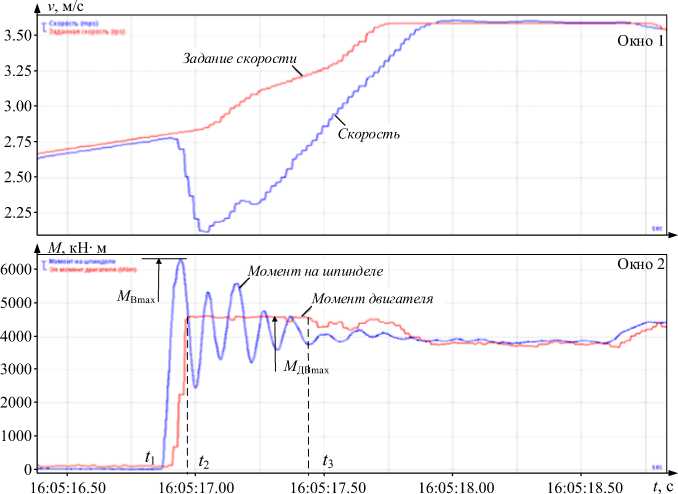
Рис. 2. Осциллограммы скоростей и моментов двигателя и шпинделя в режиме захвата с выходом на ограничение по моменту

• 1.    Постановка задачи

Вопросам ограничения динамических нагрузок при захвате металла валками посвящены научные труды многих исследователей, в том числе ученых Южно-Уральского государственного университета и специалистов ПАО «ММК» [11–13]. В этих публикациях выполнена разработка способов снижения момента шпинделя путем формирования оптимальных скоростных режимов (тахограмм) электроприводов клети. Достижение поставленной цели обеспечивается за счет предварительного замыкания угловых зазоров в шпиндельных соединениях. В работах [14, 15] дополнительно предлагается ограничение упругого момента вала за счет кратковременного интенсивного торможения после захвата. Экспериментально подтверждено, что это обеспечивает улучшение динамических показателей.

Однако поставленную проблему нельзя считать решенной, так как разработанные системы являются разомкнутыми системами задания скорости. Контроль и автоматическое регулирование момента на шпинделе не производятся. Альтернативным решением являются системы прямого регулирования упругого момента вала. Они обеспечивают высокую точность, однако для их реализации необходимо непосредственное измерение упругого момента шпинделя. Это вызывает затруднения, так как требует установки прецизионных датчиков на вращающееся оборудование [16–18].

Вместе с тем возникают проблемы и при разработке упомянутых систем автоматического управления с наблюдателями координат электромеханических устройств. В работе [3] отмечается, что задача управления особенно сложна, когда не все переменные состояния системы поддаются измерению. Это часто происходит в промышленных электроприводах и вполне относится к прокатным станам. В публикации выполнен синтез системы управления с пропорционально-интегральным (ПИ) регулятором и дополнительными обратными связями, рекомендована система с двумя обратными связями.

В работе [19] указывается, что для улучшения характеристик «классической» структуры управления с ПИ-регулятором координат можно использовать дополнительный контур регулирования по одной выбранной переменной состояния. Согласно литературным источникам, в частности [3], распространено применение дополнительной обратной связи по сигналу крутящего момента на валу. Следует заметить, что подключение такой связи предусмотрено в системе, разработка которой представлена ниже в настоящей статье.

В перечисленных и других публикациях зарубежных авторов представлены результаты математического моделирования и экспериментальных исследований, выполненных на лабораторных установках с двигателями малой мощности. Разработанные алгоритмы представляют академический интерес, однако не могут быть «напрямую» применены для управления промышленными электромеханическими системами с ударной нагрузкой.

Обоснование разработки системы

В связи с изложенным обоснована задача разработки системы компенсации динамических нагрузок неуправляемой массы (валка) средствами управляемой массы (двигателя). Для ее решения необходимы:

• 1)    разработка наблюдателя, обеспечивающего восстановление динамических процессов второй массы по непрерывно измеряемым параметрам первой массы в online-режиме;

• 2)    разработка и исследование замкнутой системы прямого регулирования скорости второй массы с подчиненным регулированием упругого момента на основе этого наблюдателя.

Разработке наблюдателей координат двух- и трехмассовых электромеханических систем, которые обеспечивают восстановление момента вала и скорости неприводной массы по параметрам электропривода, посвящены научные труды ряда выдающихся ученых. В числе значимых разработок следует отметить труды профессоров Ивановского государственного энергетического университета А.Р. Колганова и С.К. Лебедева [20–23], ученых Санкт-Петербургского государственного университета информационных технологий, механики и оптики (ИТМО) под руководством проф. В.С. Томасова [24–26], работы профессоров Донецкого государственного технического университета П.Х. Коцегуба и О.В. Толочко [27–29].

По результатам анализа этих и других публикаций обоснованы требования к «промышленному» наблюдателю координат электромеханической системы прокатного стана.

• 1.    Динамические процессы должны представляться на основе непрерывно измеряемых физических параметров при минимуме вычислительных операций.

• 2.    Координатами, доступными для контроля, являются скорость и момент двигателя, а также прикладываемый момент нагрузки. Выходными

• 3.    Разрабатываемые решения не должны требовать применения сложного математического аппарата (вычислителей) для обработки сигналов в online-режиме и должны быть реализуемыми на установленных контроллерах АСУ ТП прокатных станов.

• 2.    Основная часть

координатами являются скорость валка и упругий момент шпинделя.

Такой наблюдатель обеспечит высокое быстродействие, необходимое для регулирования динамических процессов, происходящих в двухмассовой системе при ударной нагрузке, прикладываемой ко второй массе.

Разработка наблюдателя координат двухмассовой системы

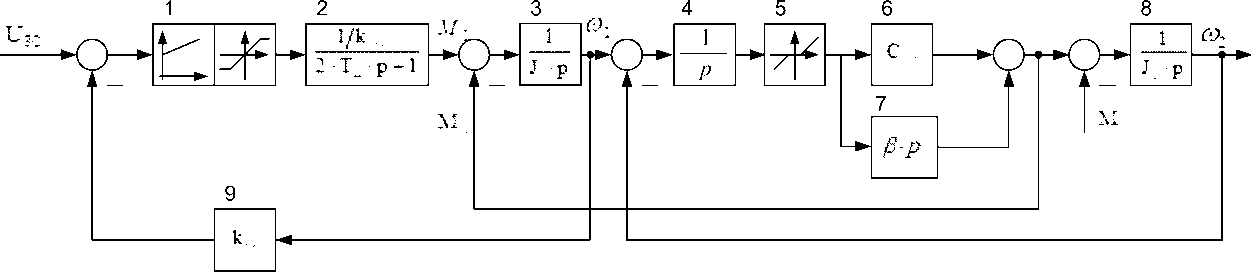
Исследуемая система «электропривод – валок» может быть представлена в виде замкнутой двухконтурной структуры (рис. 3а). Блоки 3, 5–7 являются типовыми блоками модели двухмассовой системы [30]. Они определяют характер переходных процессов в механической части, в том числе естественное затухание колебаний, блок 5 моделирует зазоры в передачах. Обратная связь по скорости моделируется блоком 9 с коэффициентом k _ос. Замкнутый контур регулирования момента представлен звеном 2.

На схеме обозначены: Т _µ – постоянная времени контура момента; J ₁, J ₂ – моменты инерции 1-й и 2-й масс; С ₁₂ – коэффициент упругости механической передачи; β – коэффициент, отвечающий за естественное демпфирование (типа вязкого трения); M ₁ – момент двигателя; M ₁₂ – упругий момент шпинделя; ω₁, ω₂ – угловые скорости первой и второй масс. Численные значения этих и других

а)

б)

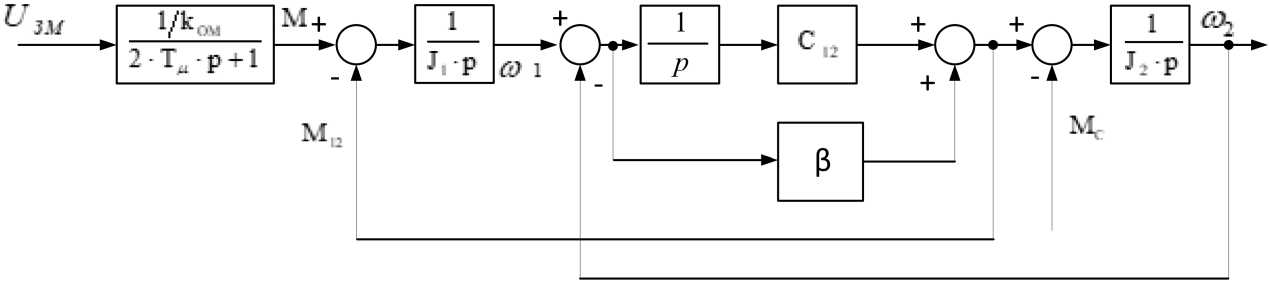
Рис. 3. Структурная схема двухмассовой электромеханической системы (а) и структура модели для разработки наблюдателя (б)

Параметры модели двухмассовой системы электропривода стана 5000

Параметр Обозначение Размерность Значение Момент инерции первой движущейся массы (двигателя) J1 кг∙м2 125 000 Момент инерции второй движущейся массы J2 кг∙м2 114 571 Жесткость упругой связи с12 Н∙м/рад 76 489 587 Собственная частота упругих колебаний ω12 рад/с 9,96 Ускорение электропривода ε0 рад/с2 1–3 Зазор в передаче δ рад 0,017–0,051 (1-3°) Средний упругий момент M12 МН∙м 1,9 Коэффициент демпфирования β Н∙м∙с/рад 100 000 Декремент затухания ξ – 0,172 Коэффициент усиления регулятора скорости kрс – 19,5 Постоянная времени регулятора скорости T рс с 0,0041 параметров, необходимые для настройки регуляторов и моделирования, приведены в таблице.

При разработке наблюдателя из этой схемы исключаются нелинейный блок 5, моделирующий зазоры, и блоки 1, 8, реализующие контур регулирования скорости. Полученная структура представлена на рис. 3б. Для нее справедлива система дифференциальных уравнений в пространстве состояний:

dM ₁ dt

r M 1 + _{т к}   M 1 ref ;

T_m     T_m K _oм

d ω    1

—1 = —M 1

dt    J ₁

-

M 12 ; J ₁

dM ₁₂

= C 12®1 dt

- C 12 ® 2 + "в M 1

J ₁

-

в JJ

J ₁· J ₂

^M 12

+ у M c ;

J ₂

d ω₂ dt

= J; m 12 - J“ M c ,

где M 1 ref – заданный момент двигателя; Т m – электромеханическая постоянная времени.

На основе этих уравнений разработан наблюдатель упругого момента, скорости 2-й массы и

момента нагрузки, его схема приведена на рис. 4. Восстановление ненаблюдаемых переменных и момента нагрузки осуществляется по сигналам скорости и момента двигателя, измеренным в реальном времени.

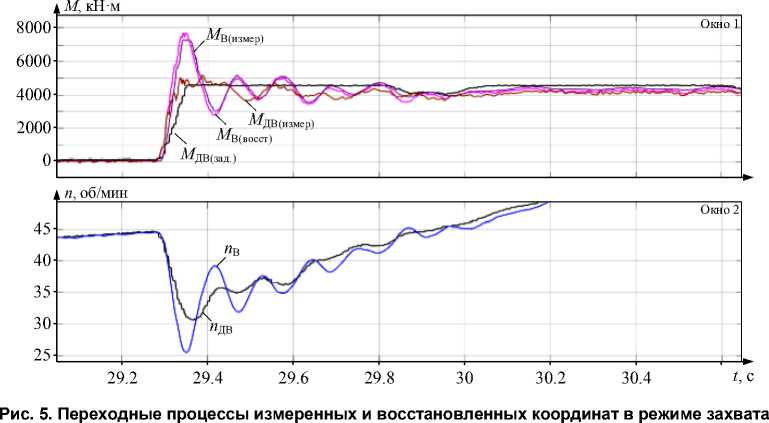
На рис. 5 представлены графики восстановленных переменных и аналогичные осциллограммы, полученные на стане в режиме захвата металла валками. Кривые упругого момента вала, полученные от наблюдателя М _В ( _восст ) и от системы измерения М _В ( _измер ) , соответствуют друг другу как по характеру, так и по амплитудным значениям. Их совпадение обеспечивается с погрешностью не выше 5 %. Кривые скоростей n ДВ и n В сопоставить нельзя, так как они относятся к разным массам.

Представленные осциллограммы являются примером, подтверждающим удовлетворительную точность восстановления упругого момента шпинделя в режиме ударного приложения нагрузки. Аналогичные результаты получены при прокатке заготовок различных профилей в разных проходах. Это позволило рекомендовать разработку замкнутой САР координат двухмассовой системы на основе рассмотренного наблюдателя.

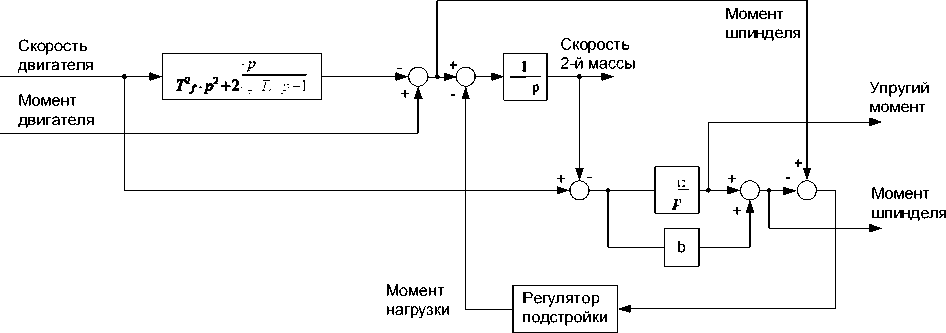
Рис. 4. Структурная схема разработанного наблюдателя

Разработка замкнутой системы регулирования координат неуправляемой массы

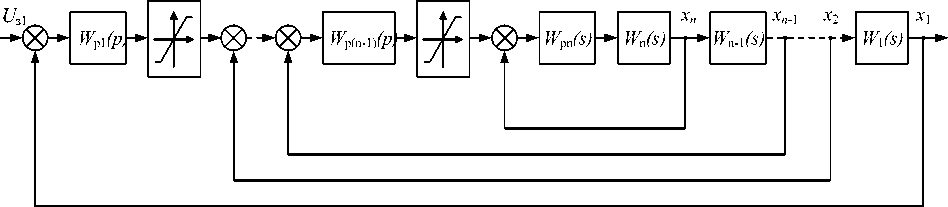
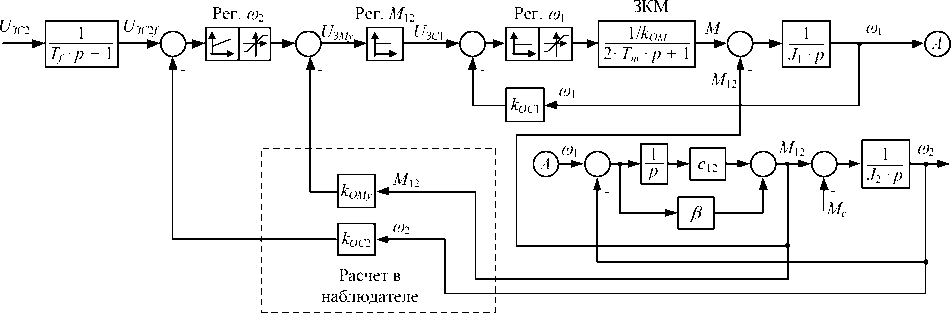
Система автоматического регулирования разработана исходя из структуры объекта управления, представленной на рис. 3а. При ее разработке за основу приняты теоретические положения замкнутых систем с ограничением моментов в механических передачах, обоснованные в книге А.Р. Колганова [20]. Структура системы с ограничением сигналов на входах регуляторов внутренних контуров представлена на рис. 6а. Для выполнения функций ограничения используются нелинейные блоки с насыщением. По этому принципу разработана система, схема которой приведена на рис. 6б. Она представляет собой замкнутую трехконтурную САР скорости второй массы с подчиненными контурами упругого момента, скорости и момента двигателя. При таком построении возможно ограничить не только задание на контур момента двигателя, но и задание на контур регулирования упругого момента.

U p2       U з2                    U p n       U з n

а)

б)

Рис. 6. Структуры системы с ограничением сигналов на выходах регуляторов (а) и разработанной трехконтурной САР скорости второй массы (б)

На рис. 6 показаны: внешний ПИ-регулятор (Рег.ω₂) скорости 2-й массы J ₂; регулятор Рег. M ₁₂ упругого момента; регулятор скорости (Рег.ω 1 ) первой массы J 1 , его выходом является задание на момент двигателя. Передаточные функции регуляторов синтезированы по правилам настройки кон-

Передаточная функция регулятора скорости ω 2 второй массы:

W PC2 ^{( P} ) =

k ом ■ J 2

8 Т _Ц^ к ос

Для задания астатизма последовательно с ним

туров подчиненного регулирования координат [31]. Получены следующие функции:

включается корректирующее звено с передаточной функцией (на рис. 6б не показано):

W pci ( P ) =

11 — 2 Т _Ц P W oci ( P )

k ом ' J 1

^{2 T}< k ос

– для ре-

Wk(P)=

8 Т _Ц P + 1 8 Т _Ц P

гулятора скорости двигателя;

1 k p

^WPM12 (P ) =     ----;--Для Регуля-

4 T P k ом ^с12 +P P

тора упругого момента.

Если учитывать коэффициент затухания β, то

Очевидно, что промышленному внедрению разработанной системы должны предшествовать исследования методом моделирования. Как показано на схеме рис. 6б, в ней обеспечивается ограничение упругого момента. Поэтому наибольший

1 к

W PM12 ( P ) = "7227 ■ Тос" ■ ^{4 Т} ц k ом

(в ~ с12 I ---P + 1 к с12

,

интерес вызывает анализ переходных процессов при размыкании контура регулирования скорости двигателя, обусловленных данным ограничением.

без учета коэффициента β

W PM12 ( P ) = ТТ^ос---- ^{4 Т} ц ^ k ом ■ ^с 12

.

3. Результаты исследований

Результаты имитационного моделирования

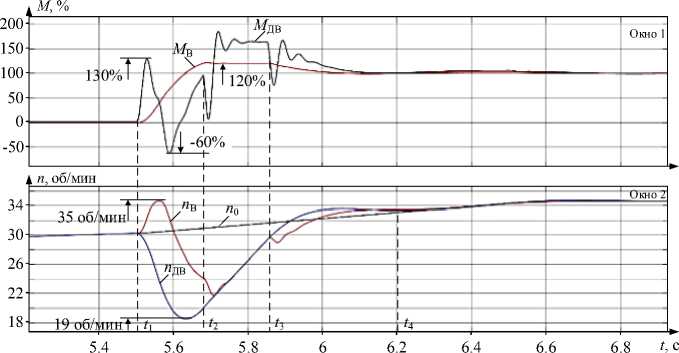
На рис. 7а приведены результаты моделирования процессов при заданных ограничениях: упругого момента на уровне 120 % и момента двига-

а)

б)

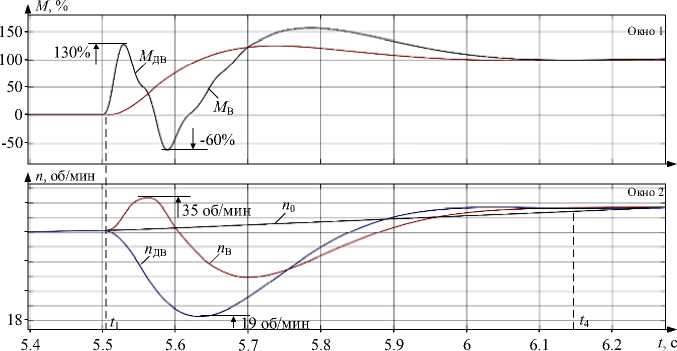
Рис. 7. Переходные процессы моментов и скоростей при ударном приложении нагрузки с ограничением (а) и без ограничения (б) упругого момента

Электромеханические системы теля на уровне 240 %. Последнее значение соответствует существующей настройке регулятора скорости двигателя. На рис. 7б представлены аналогичные процессы без выхода регуляторов на ограничение. Захват металла валками происходит в момент времени t ₁ на участке ускорения двигателя при замкнутых угловых зазорах.

Момент двигателя в обоих случаях не достигает ограничения. На рис. 7а момент на валу шпинделя ( М В ) в момент времени t 2 достигает величины 120 % и удерживается на этом уровне системой регулирования. Таким образом реализуется ограничение упругого момента на шпинделе. В результате в интервале t ₂ – t ₃ привод работает при разомкнутом контуре регулирования скорости 2-й массы. Вследствие этого переходный процесс момента двигателя М Д _В приобретает сложный характер, момент изменяется в диапазоне –60…+130 %. На рис. 7б размыкания контура скорости 2-й массы не происходит. Переходные процессы скоростей первой и второй масс ( n ДВ , n В ) в обоих случаях продолжаются примерно одинаковое время в интервалах t 1 – t 4 . Динамические отклонения скоростей также находятся в одинаковых диапазонах: 19–35 об/мин при скорости захвата 30 об/мин. Таким образом, диапазон отклонений скоростей относительно заданной составляет –37…+17 %).

Из представленных временных зависимостей следует вывод, что разница (ошибка регулирования) скоростей 1-й и 2-й масс в обоих случаях имеет место только во время переходных процессов (в течение 0,5–0,7 с после приложения нагрузки). В это время проявляются упругие свойства двухмассовой системы. В целом обеспечиваются астатическое регулирование обеих скоростей с удовлетворительным быстродействием и ограничение упругого момента.

Далее дана оценка целесообразности увеличения быстродействия контуров регулирования скоростей 1-й и 2-й масс. Для этого коэффициент регулятора скорости второй массы (Рег.ω2) увеличен в 2 раза, и уровни ограничения обоих моментов установлены равными 240 %. Расчетные зависимости представлены на рис. 8. В этом случае момент двигателя МДВ достигает ограничения. Упругий момент МВ на валу изменяется аналогично зависимости на рис. 7б и нарастает без перерегулирования. Характер переходных процессов скоростей на рис. 7б, 8 различается, однако их время одинаково и составляет около 0,5 с.

Сравнение расчетных зависимостей на рис. 7б и рис. 8 позволяет сделать вывод, что быстродействие контура регулирования скорости второй массы не оказывает существенного влияния на показатели регулирования момента на валу двухмассовой системы.

С целью обобщенной оценки динамических свойств на рис. 9а представлены логарифмические амплитудно-частотные характеристики (ЛАЧХ), построенные для традиционной двухконтурной САР скорости с ПИ-регулятором – характеристика 1 и предложенной трехконтурной системы без учета нелинейностей, связанных с ограничением сигналов, – характеристика 2. При их построении входным сигналом является задание скорости, контролируемым – скорость второй массы. Из них следует, что для скорости второй массы предложенная система обеспечивает большую полосу пропускания, следовательно, обладает менее колебательными свойствами.

На рис. 9б приведены ЛАЧХ и ЛФЧХ, построенные при разомкнутом внешнем контуре. Их анализ позволяет сделать следующие выводы.

– Запас по амплитуде составляет 10 дБ, что, согласно критерию Найквиста, является достаточным.

– ФЧХ клювовидная, переходов через –180° левее частоты среза нет; запас по фазе около 50°, чего также вполне достаточно.

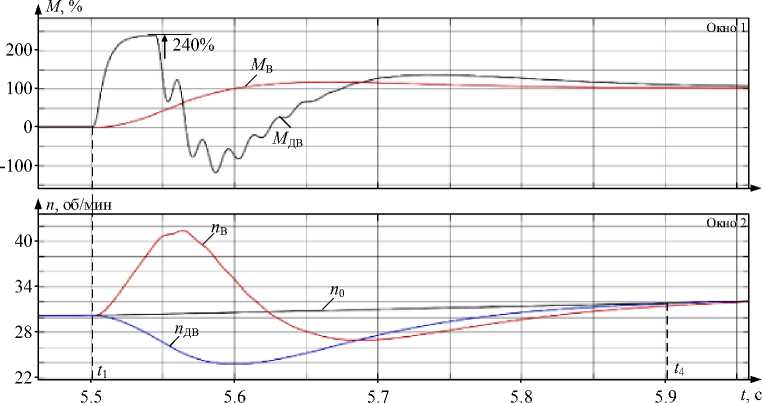
Рис. 8. Переходные процессы, аналогичные рис. 7, при увеличенном коэффициенте регулятора скорости второй массы

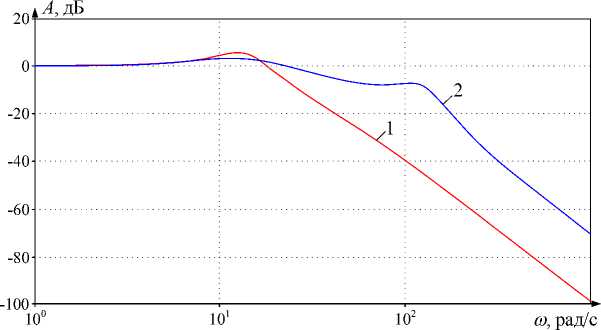
а)

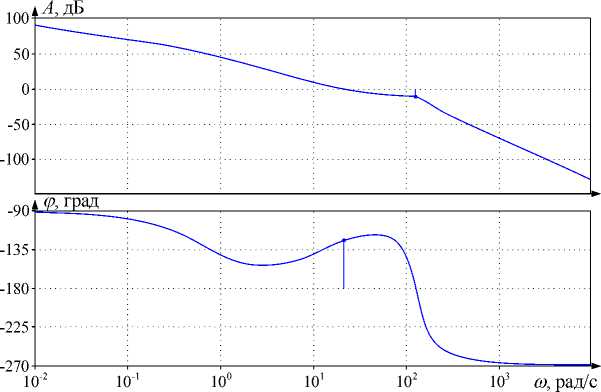
б)

Рис. 9. ЛАЧХ замкнутых контуров регулирования скорости (а), ЛАЧХ и ЛФЧХ при разомкнутом внешнем контуре (б)

Аналогичные частотные характеристики были построены для рассмотренной «более жесткой» настройки регулятора скорости 2-й массы (здесь не приводятся). Сравнение характеристик позволило сделать вывод, что увеличение коэффициента усиления в два раза незначительно влияет на резонансную частоту и амплитуду колебаний 1-й массы.

Таким образом, проблем с устойчивостью разработанной системы независимо от настройки регулятора 2-й массы во всем диапазоне частот нет.

Экспериментальные результаты

Алгоритм разработанного наблюдателя упругого момента и скорости валка технически исполнен в программном обеспечении промышленного контроллера клети стана 5000. Проведены опытнопромышленные испытания, получено большое количество восстановленных зависимостей и экспериментально снятых осциллограмм.

По результатам обработки более 100 зависимостей, аналогичных представленным на рис. 5, сделаны следующие выводы.

– В режиме захвата при предварительно замкнутых угловых зазорах в шпиндельных соедине- ниях средняя разница амплитудных значений измеренного и восстановленного моментов составляет 5–7 %;

– Аналогичная разница в режиме захвата при разомкнутых зазорах достигает 10–15 %.

Это подтверждает известный вывод, что динамическая составляющая момента, обусловленная непосредственно ударом при замыкании углового зазора, относительно невелика. В работе [32] показано, что амплитуда динамического момента при упругом ударе (первая составляющая) не сильно зависит от величины углового зазора. При номинальном моменте двигателя 1,9 МН∙м и угловом зазоре 1,5° она составляет 2,7 %. В то же время амплитуда составляющей, обусловленной упругими свойствами шпинделя, в 10–15 раз превышает амплитуду первой составляющей и за счет этого оказывает более сильное влияние на динамический момент при захвате.

В целом по результатам экспериментов сделаны следующие выводы.

• 1.    Разработанный наблюдатель обеспечивает восстановление координат упругого момента и

• Электромеханические системы скорости валка с точностью, достаточной для практических целей. Это создает предпосылки для промышленных испытаний представленной замкнутой системы автоматического регулирования скорости второй массы с ограничением момента на шпинделе.

• 2.    В настоящее время наблюдатель находится на стадии опытно-промышленной эксплуатации. Проводится длительный пассивный эксперимент, целями которого являются подтверждение справедливости выводов и оценка возможных рисков при внедрении системы управления на его основе.

• 4.    Обсуждение результатов

Анализ временных зависимостей, представленных на рис. 7а, показывает, что переходный процесс момента двигателя в системе с наблюдателем имеет сложный характер и изменяется в диапазоне –60…+130 %. По сравнению с монотонным процессом момента на валу его переходный процесс ухудшается. Однако целями подключения внешнего контура являются исключение колебаний упругого момента и его ограничение на допустимом уровне. В исследуемом случае его изменение близко к настройке на модульный оптимум. Это позволяет утверждать, что цель регулирования достигнута.

Контур момента двигателя является подчиненным, это объясняет, почему форма кривой этого параметра является сложной. Но для синхронного двигателя колебания в диапазоне, указанном на рис. 7, не являются опасными. Поэтому можно сделать вывод, что переходные процессы моментов двигателя и шпинделя являются удовлетворительными.

Преимуществами разработанного наблюдателя являются простота настройки и возможность получения достоверных переходных процессов. В результате сравнения восстановленных и промышленных сигналов подтверждена удовлетворительная точность вычисления упругого момента с погрешностью 5–15 %.

Заключение

Рассмотрен наблюдатель, обеспечивающий непрерывный контроль координат двухмассовой электромеханической системы клети прокатного стана. На его основе разработана трехконтурная система прямого регулирования скорости валка, обеспечивающая ограничение упругого момента в режиме ударного приложения нагрузки. При ее разработке за основу принята многоконтурная система регулирования координат с ограничением входных сигналов подчиненных контуров, рассмотренная в научных трудах проф. А.Р. Колганова.

Обосновано подключение следующих регуляторов:

– пропорционального регулятора скорости первой массы, его выходом является задание на момент двигателя;

– пропорционального регулятора упругого момента. Такая настройка является оптимальной, так как в структуре объекта есть интегратор, а данный регулятор обеспечивает высокое быстродействие;

– пропорционального регулятора скорости второй массы с корректирующим пропорционально-интегральным звеном на входе. Это звено повышает наклон ЛАЧХ в низкочастотной области и обеспечивает астатическое регулирование скорости второй массы.

Анализ переходных процессов, полученных методом математического моделирования, подтвердил снижение амплитуды упругого момента шпинделя и удовлетворительный характер переходных процессов момента и скорости двигателя. Аналогичные выводы сделаны по результатам построения ЛАЧХ и ЛФЧХ разработанной системы.

По результатам обработки более 100 экспериментальных зависимостей дано заключение, подтвердившее данные выводы.

Представленные разработки выполнены на примере электропривода клети стана 5000. Они рекомендуются для применения на других агрегатах, электроприводы которых работают с ударным приложением нагрузки. К таким агрегатам относятся практически все станы горячей прокатки и черновые группы клетей сортовых станов.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках субсидии на финансовое обеспечение выполнения государственного задания (фундаментальное научное исследование), договор № FENU-2020-0020 (2020071ГЗ).