Регулирование механических координат вентильного электропривода методом векторного управления

• 1.    Постановка задачи исследования

• 2.    Обеспечение максимального
  
  электромагнитного момента двигателя

При разработке управляемого электропривода, как правило, ставится задача обеспечения заданного диапазона регулируемых координат. Чаще всего такими координатами являются электромагнитный момент и скорость вращения электродвигателя. В любом электроприводе ставится задача обеспечения максимального электромагнитного к.п.д. двигателя во всех режимах работы или в основном рабочем режиме. В частности, для обеспечения требуемого быстродействия манипуляторов для устройств реабилитации и диагностики в медицинской технике [1] необходимо минимизировать время разгона и торможения исполнительного органа в переходных режимах, которые являются основными рабочими режимами. Для этого необходимо обеспечить максимальный момент двигателя при имеющейся скорости и напряжении первичного источника, а к.п.д. не является важнейшим показателем. Для расширения диапазона отрабатываемых углов манипулятора мы должны увеличить скорость холостого хода двигателя при ограниченном напряжении первичного источника питания, не ставя первостепенной задачей обеспечение максимума к.п.д. Однако при установившемся плавном движении манипулятора или при реализации режима притормаживания с рекуперацией энергии, особенно при работе от автономного переносного источника питания, входящего в состав реабилитационно-диагностического комплекса, такая задача возникает.

Все перечисленные задачи могут быть достаточно эффективно решены при использовании вентильного электропривода на основе синхрон- ного двигателя (СД) с возбуждением от постоянных магнитов с векторным управлением. Причём в отличие от широко распространённых методов векторного управления путём автономного регулирования токов по осям d и q, требующих привлечения значительных вычислительных ресурсов [2–4], управление предлагается осуществлять путём регулирования угла коммутации (θ) [5], которое при наличии датчика углового положения ротора реализуется простейшими средствами. В представленной статье приводятся теоретические предпосылки для такой реализации. При этом рассматриваются только установившиеся режимы работы привода и предполагается, что ШИМ-регулирование амплитуды фазного напряжения осуществляется идеально без дополнительных потерь. Проблемы, связанные с оговорёнными допущениями, требуют дополнительного исследования и не входят в задачи данной статьи.

Предположим, что в режиме векторного управления на фазные обмотки двигателя поступает симметричное трёхфазное напряжение. Представим уравнения напряжений статорной цепи СД во вращающейся системе координат в относительных единицах с учётом общепринятых допущений о симметрии статорной обмотки, равенстве индуктивных сопротивлений двигателя по осям d и q , отсутствии влияния реакции якоря и т. д. [6]:

• ^{Y Si}nO    l ^ ^Тэ 8! д ^{+ Т}э ^ ;

Ycos9 = l q + Т э &1_й + Т э ^^" + ^£ .

Здесь у = ~— относительное значение амплитуды фазного напряжения; U и U_a - соответственно, фактическое и номинальное значение амплитуды фазного напряжения; i_d и i_q - относительное значение токов по соответствующим осям, при базовом значении тока L = -—, где г - активное со- б 2г’

.      „ -              Е    кФт противление фазной обмотки; е = — = —--отно сительное значение скорости двигателя, где Е -амплитуда фазной э.д.с., кФ - коэффициент связи между мгновенной скоростью двигателя и амплитудой фазной э.д.с., ω – абсолютная скорость вра-m0L щения ротора; тэ = — - относительная электромагнитная постоянная времени фазной обмотки, иа ю0 = — - скорость идеального холостого хода (базовая скорость); т = m0t - относительное время.

Из приведённой системы уравнений просто определить токи i_d и i_q , которые в принятой системе относительных единиц для установившегося

е2тэ

9Птах = arctg еТэ - arcsin . + ■

Для оценки адекватности выражения (4) получим в общем виде аналитическое соотношение для расчёта электромагнитного к.п.д. В [9] приве-

дено аналитическое выражение для определения потребляемой синхронным двигателем активной мощности, которое в принятой системе относи-

тельных единиц получит вид

_ yе(ет3sin9—cos9)+y2

^Рап =       1+(ет_э)²

.

Электромагнитный к.п.д. определяется соот-

ношением

ηэ

Р э ^р ап

где Р э = i q е. Подставив р^ и Р э в выражение для

к.п.д., получим yе(ет3sin9+cos9)—е2 п = —--------—г.

^э     yе(ет₃sin9—cos9)+y²

режима получат вид:

_ y(етэcos9—sin9)—е2тэ

=       1+(ST э )^{2      ;}

.   y(ет3sin9+cos9) — е

^{1 q} =       1+(ет э )²      .

(1а)

(1б)

По выражению (5) рассчитана кривая пэ = /(9) при у = 1, е =0,8 и тэ = 1,2 (рис. 1). На этом рисунке отмечена точка 1, соответствующие углу обеспечивающему максимальный к.п.д., рассчитанному по выражению (4), а также точка 2, соот-

Если в качестве базового момента двигателя взять М б = кФ1_б, то согласно общей теории электромеханического преобразования энергии можно

считать относительное значение электромагнитно-

ветствующая максимальному значению к.п.д., рассчитанному по выражению (5).

Очевидно, что точки 1 и 2 зависимости пэ (9), как по значению угла, так и по значению к.п.д. не совпадают. Поскольку выражение (5) получено строго в соответствии с теорией синхронных ма-

го момента двигателя равным относительному значению тока р = i_q .

В [7] показано, что угол коммутации, соответствующий максимальному установившемуся зна-

шин, то вызывает сомнение справедливость выражения (4). В частности, требует проверки утверждение о том, что выполнение условия id = 0 обеспечивает максимум электромагнитного к.п.д.

чению электромагнитного момента двигателя, можно найти, определив производную diq/d9 и приравняв её к нулю. При этом в принятой систе-

двигателя.

ме единиц получим для двигательного режима

9д    = arctg ет.

^р тах             ^э

Дело в том, что выполнение этого условия позволяет обеспечить при заданной электромагнитной мощности минимум полной, активная плюс реактивная составляющие, потребляемой мощно-

Очевидно, что для обеспечения максимального тормозного момента необходимо установить угол

сти, которая определяется в относительных единицах соотношением [9]

θт ртах

= 9„ ртах

+ п.

y² — 2yеcos9+е^{2 р} пп = ^у ^    1+(ет э ) 2

.

Можно отметить, что

полная и активная по-

требляемые мощности связаны известным соот- ношением

Рап = РппСО5ф, где φ – угол между векторами напряжения и тока.

Определим к.п.д. по полной потребляемой мощности

Р э п = — п ^р пп

yе(ет3sin9+cos9)—е2 y7[1+(ет3)2](y2 — 2еycos9+е2) .

По выражению (6) на рис. 1 при тех же параметрах двигателя построена зависимость пп (9). Мы видим, что для этой зависимости максимум к.п.д. по полной потребляемой мощности (точка 3) соответствует углу θη , рассчитанному по формуле (4).

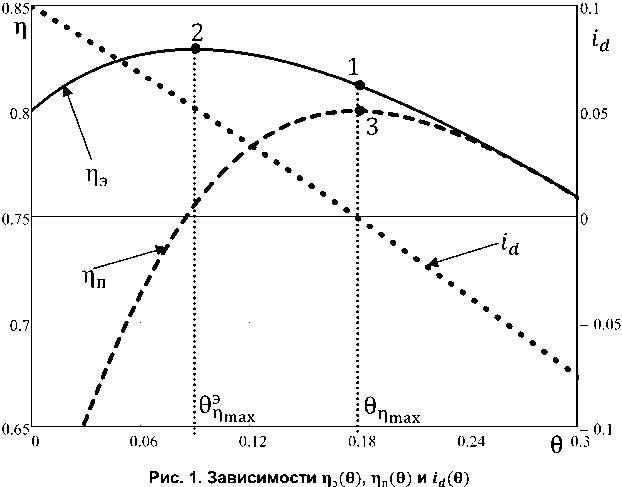
Следовательно, выражение (4) позволяет осуществить настройку угла θ из условия обеспечения минимума полной потребляемой мощности (максимум ηп), но при этом не гарантирован минимум электрических потерь в обмотке якоря, который обеспечивает максимум электромагнитного к.п.д. ηэ, что очень важно с точки зрения облегчения теплового режима двигателя.

Формула для определения угла θ, соответст-

только для экстренного торможения. Из соображений энергетической эффективности более рационально использование рекуперативного торможения путём регулирования амплитуды фазного напряжения двигателя γ. При этом угол коммутации также должен определяться согласно (7) при γ ≤ ɛ.

4. Обеспечение максимальной

вующего максимуму электромагнитного к.п.д. ηэ, получена из выражения (5) путём поиска экстремума функции и имеет следующий вид

θэ nmax

= 2arctg

(у-8)(-1+У1 + (8Т э )²)

8Т э ⁽Y⁺8)         ^.

скорости вращения

Сначала найдём значение угла коммутации, при котором обеспечивается максимальная скорость холостого хода. Для этого, воспользовавшись соотношением (1б), решим уравнение i_q = 0 относительно ɛ. В результате получим значение

В частности, для кривых, изображённых на рис. 1, для случая у = 1, £ = 0,8 и т э = 1,2, значения 0Щ_тах и @_Птах будут следующими: 0П_тах = 0,089 и

скорости холостого хода в виде

^£хх =

ycosO 1-утэ sin0.

θ nmax

= 0,178.

Необходимо отметить интересный факт, ко-

торый следует из рис. 1. Путём регулирования угла θ удаётся получить электромагнитный к.п.д. вентильного двигателя больше по величине отно-

Найдём экстремум полученной функции традиционным способом. В результате решения получим значение угла θ, соответствующее максимальной скорости

0 Х^х = arcsin ут_э. (9) ® max ^э

сительной скорости вращения ротора ɛ, что невоз-

можно для асинхронного или коллекторного двигателя. Более того, чем больше относительное значение индуктивного сопротивления обмотки якоря (ετ_э), тем ближе максимальное значение к.п.д. к единице. Наконец, если найти предельное значение п_э по выражению (5) при £т_э ^ ад , то, оказывается, оно равно 1.

Что касается повышения электромагнитного к.п.д. в тормозном режиме, то осуществление торможения путём изменения угла коммутации с точки зрения экономии энергии неэффективно, так как в этом смысле эквивалентно торможению противовключением, и может быть рекомендовано

Подставим найденное значение угла в выражение (8) и получим максимальное значение ско-

рости холостого хода

„хх _ ---у---

^£тах  VT-Y^ "

Выражение (10) показывает, что зависимость

скорости от угла имеет экстремум в виде точки перегиба только при выполнении условия |утэ | < 1. Однако реальные значения τэ могут быть в разы больше единицы. В этом случае приведённая методика поиска максимальной скорости холостого хода не пригодна.

На рис. 2 представлены зависимости скорости холостого хода от угла коммутации ехх = /(0), рассчитанные по выражению (8) при у = 1 и раз-

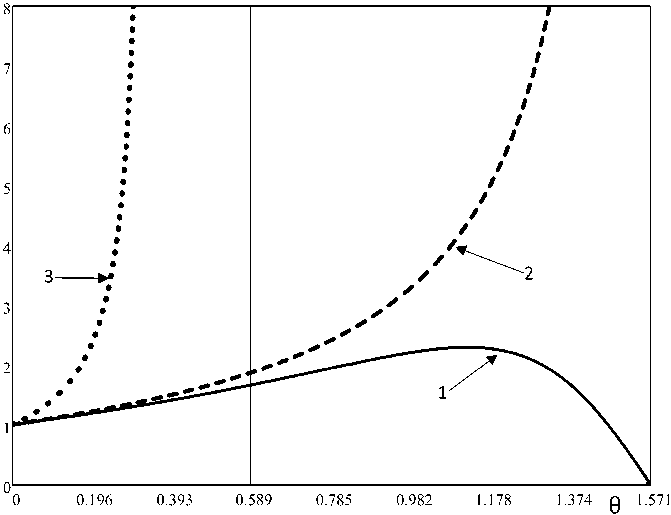
Рис. 2. Скорость холостого хода: кривая 1 - е_хх при т э = 0,9 ; кривая 2 - Е хх при т э = 1 ; кривая 3 - е_хх при т э = 3

личных значениях т э = 0,9; 1; 3, которые подтверждают сказанное выше.

Действительно, при тэ = 0,9 функция скорости имеет явно выраженный экстремум. В двух других случаях он отсутствует и максимум скорости стремится к бесконечности. Тогда максималь- ную скорость лучше определять численно, как это показано ниже.

Предположим, что перед нами стоит задача получения заданной относительной скорости двигателя при имеющемся значении относительного момента. Перепишем уравнение (1б) в виде

Y(cos6 + етэ sin6) = р[1 + (етэ )2] + е      (11)

и разрешим его относительно θ. В результате определим значение угла, при котором для известных γ и μ получим требуемое значение ε

£Т э -7 ^{( ет} э ) ^{2- (}№ ^{+ ( ет} э ) ^{2 ]+}£^}/Y) ^{2 + 1}

• ⁶ = ^2arc^tg        № + (ет₃ ) 2 ] + ₆ }/ _Y +1        .     ⁽¹²⁾

Если в результате расчёта по выражению (12)

мы получим вещественное положительное значение угла 6 < п/2, то поставленная задача может быть решена. В противном случае можно заключить, что при имеющихся значениях управляющего сигнала и параметрах двигателя заданное значение скорости не может быть обеспечено.

Теперь решим задачу определения максимального достижимого значения скорости двигателя при заданных параметрах, нагрузочном мо- менте, номинальном или максимально допустимом напряжении. Для этого разрешим уравнение (11)

относительно скорости:

е =

Yт_э sin6 -1 +J4YЦт_э²cos6-4^² т э ²+Y²т_э²sin² 6-2Yт_эsin6+1

. (13)

С помощью этого соотношения необходимо найти угол θ, соответствующий максимальной скорости. Однако получение этой аналитической зависимости представляет определённые трудности.

Численные расчёты показывают, что при наиболее вероятных практических значениях т э < 3 угол, соответствующий максимальному значению скорости ε при заданных значениях γ и μ, может быть найден по простому приближённому выражению

⁶« тах = ^тэ ⁽Y ^- Н) ⁽¹⁴⁾

Полученное значение угла коммутации подставим в выражение (13) при у = 1 и найдём максимальное значение скорости, которую может развить двигатель при заданном значении параметров и нагрузочного момента.

Для подтверждения возможности использования приближённого соотношения (14) был осуществлён численный поиск угла, соответствующего максимальной скорости по выражению (13), и определение этого угла по выражению (14). Результаты расчёта при р = 0,1 _ 0,9 и т э = 0,6 _ 1,2 сведены в таблицу, где первые два столбца (1-й и 2-й) для каждого значения т э соответствуют численно найденному значению угла, при котором скорость достигает максимума, и собственно максимальному значению скорости, а следующие два столбца (3-й и 4-й) соответствуют приближённо вычисленному значению угла (по формуле (14)) и значению скорости при этом приближённом угле коммутации. Строки таблицы соответствуют различным значениям относительного нагрузочного момента. Сравнение значений максимальной ско-

Значения максимальной скорости вращения

Тэ 0,6 0,8 1 1,2 0m £m ^ 0m ^m 0m £m ^ 0m ^m 0m £m ^m ^m 0m £m ^ 0m ^m µ 0,1 0,558 1,04 0,54 1,039 0,761 1,19 0,72 1,188 0,968 1,452 0,9 1,444 1,143 1,832 1,08 1,821 0,3 0,415 0,735 0,42 0,735 0,546 0,759 0,56 0,759 0,667 0,787 0,7 0,786 0,772 0,811 0,84 0,807 0,5 0,291 0,499 0,3 0,499 0,379 0,497 0,4 0,497 0,458 0,493 0,5 0,492 0,529 0,487 0,6 0,485 0,7 0,174 0,294 0,18 0,294 0,227 0,289 0,24 0,289 0,276 0,283 0,3 0,283 0,32 0,277 0,36 0,276 0,9 0,059 0,099 0,06 0,099 0,078 0,098 0,08 0,098 0,096 0,096 0,1 0,096 0,113 0,095 0,12 0,095 рости, полученных путём численного решения и по приближённой методике показывает, что их отличие для самого наихудшего случая не превышает 0,6 %.

Из таблицы мы видим также, что путём регулирования угла коммутации можно обеспечить скорость вращения существенно выше скорости идеального холостого хода (е = 1).

Очевидно, представляет интерес оценка энергетических затрат, необходимых для обеспечения высокой скорости вращения электродвигателя. Для этого по выражению (5) были проведены расчёты электромагнитного к.п.д. η_э с различным моментом на валу, когда угол θ выбирался из условия обеспечения максимально достижимой для данного момента скорости (кривая η^′_э). Результаты расчёта при y = т э = 1 представлены на рис. 3. Там же приведена зависимость к.п.д. п э (ц), когда угол О выбирается из условия обеспечения максимального к.п.д. для данной скорости в соответствии с выражением (7) (кривая П э ), а также зависимость максимальной скорости £_тах(ц).

Мы видим, что стремление повысить скорость вращения двигателя приводит к резкому уменьшению его электромагнитного к.п.д. Физически это объясняется тем, что для повышения скорости вращения мы должны ослабить магнитное поле машины, и такое ослабление осуществляется за счёт увеличения тока id, который при полученных значениях угла коммутации имеет отрицательное значение, т. е. является размагничивающим. Аналогичное утверждение имеется и у других авторов [10].

Это положение подтверждают зависимость id(0) при различных значениях тэ и постоянной скорости вращения ротора ɛ (пример этой зависимости приведён на рис. 1).

На рис. 1 видно, что при О = ОП_тах, который определяется согласно (7), имеем i_d > 0 и максимум электромагнитного к.п.д. При О = О_Пта > ОП_тах, который определяется согласно (4) имеем ток i_d = 0, что соответствует максимуму к.п.д. по полной потребляемой мощности. По мере дальнейшего увеличения О ток i_d меняет знак и увеличивается по модулю.

Можно отметить, что положительное значение тока i_d необходимо для компенсации индуктивной составляющей тока, обусловленной индуктивностью обмотки статора, и при О = ОП_тах как раз осуществляется полная компенсация этой составляющей. Отрицательный ток i_d создаёт раз-

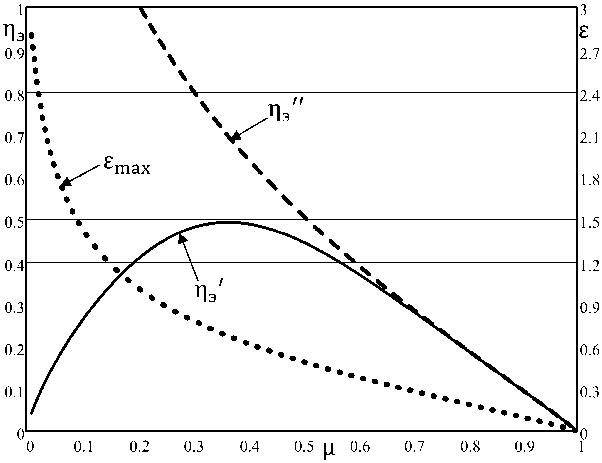
Рис. 3. Зависимости электромагнитного к.п.д. от момента при различной настройке угла коммутации

магничивающее воздействие и способствует расширению диапазона скоростей привода.

Заключение

Таким образом, поставленные в исследовании задачи решены и получены относительно простые аналитические выражения для регулирования угла коммутации в процессе векторного управления электроприводом:

– из условия обеспечения максимального момента – выражение (2);

– из условия обеспечения максимального к.п.д. по полной потребляемой мощности – выражение (4);

– из условия обеспечения максимального электромагнитного к.п.д. – выражение (7);

– из условия обеспечения максимальной скорости вращения при известном нагрузочном моменте – выражение (14).

Кроме этого, получены следующие аналитические зависимости:

– формула для расчёта угла коммутации, при котором для известных напряжения и момента сопротивления обеспечивается требуемое значение скорости – выражение (12);

– формула для расчёта скорости при заданных параметрах двигателя, нагрузочном моменте и напряжении – выражение (13).

Все предлагаемые в исследовании теоретические положения подкреплены конкретными расчётами и компьютерным моделированием.