Регулируемый элемент назначения веса волоконно-оптических ЦАП

Волоконно-оптические цифро-аналоговые преобразователи (ВОЦАП) предназначены для подключения источников бинарных оптических сигналов к общей оптической магистрали и последующего преобразования набора входных оптических сигналов в пропорциональный квантовый аналоговый оптический сигнал. Основными требованиями к ВОЦАП являются возможность подключения 8–14 цифровых источников информации при использовании серийных волоконно-оптических технологий и стандартного оборудования для их изготовления, а также совместимость по массогабаритным показателям с датчиковой аппаратурой и интегрально-оптической схемотехникой [1, 2].

В общем случае параллельный ВОЦАП должен выполнять две операции: назначение веса каждому разряду и суммирование оптических сигналов с весовыми коэффициентами, выбираемыми разрядными цифрами. Значения весовых коэффициентов определяют элементы назначения веса (ЭНВ), входящие в состав ВОЦАП. В основу принципа действия ЭНВ могут быть положены такие эффекты, как изменение геометрии оптического волокна (макроизгибы), изменение внутренних напряжений оптических волокон (ОВ) (микроизгибы), изменение взаимного положения торцов ОВ, введение дополнительных диа

Юдин Артем Анатольевич, консультант отдела информационных систем филиала «Макрорегион Поволжье» ООО ИК «Сибинтек».

фрагмирующих элементов между торцами ОВ [3, 4]. Недостатками указанных конструкций являются большие габариты, сложность конструкции и невысокая точность, а также невозможность точной подстройки регулировки коэффициента передачи [5]. В связи с этим рассмотрим конструкцию регулируемого ЭНВ с эксцентрично вращающимся круглым экраном в зазоре между передающим и приемным световодами [6].

КОНСТРУКЦИЯ ЭЛЕМЕНТА НАЗНАЧЕНИЯ ВЕСА С ЭКСЦЕНТРИЧНО ВРАЩАЮЩИМСЯ ЭКРАНОМ

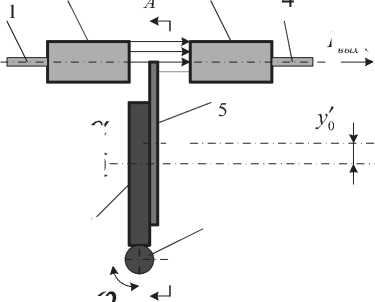
Конструкция такого ЭНВ схематично представлена на рис. 1

ЭНВ содержит передающий моноволокон-ный световод, расположенный в фокусе коллимирующей градиентной цилиндрической линзы (ГЦЛ) 2. Приемная (фокусирующая) ГЦЛ 3 расположена соосно с передающей ГЦЛ 2. В фокусе ГЦЛ 3 расположен торец приемного моно-волоконного световода 4. В зазоре между ГЦЛ 2 и 3 расположен круглый непрозрачный экран 5, соединенный по плоскости с червячным колесом 7, которое приводится во вращение с помощью червяка 6. Геометрический центр экрана 5 смещен относительно центра вращения колеса 7 на величину эксцентриситета ε . При повороте червяка на угол ϕ происходит поворот червячного колеса на угол α = ϕ / k , где k - коэффициент передачи червячной пары. Одновременно с колесом поворачивается экран 5, что приводит к экранированию части светового потока, проходящего из ГЦЛ 1 в ГЦЛ 2. При соответствующем выборе значения эксцентриситета степень перекрытия зависит от углового положения экрана и может изменяться от 0 до 1.

A - A

Р ых ( ^а )

P

ОЛ

α

ϕ _A

Z x 0

I /

α

ϕ

Рис. 1. Конструкция ЭНВ с эксцентрично вращающимся экраном

Описанная конструкция позволяет добиться плавной, а следовательно и более точной, регулировки коэффициента передачи излучения между ГЦЛ. Плавность регулировки тем выше, чем больше коэффициент передачи редуктора и чем больше диаметр экрана по сравнению с диаметром ГЦЛ.

К достоинствам данной конструкции можно отнести её повышенную виброустойчивость за счет эффекта самоторможения в червячной передаче. Для изготовления миниатюрных конструкций ЭНВ данного типа с успехом могут быть использованы технологии серийно выпускаемых многооборотных подстроечных резисторов. Например, при использовании редуктора потенциометра СП5-3 с передаточным отношением k = 46 возможно создание миниатюрной конструкции ЭНВ с габаритами 13х13х3,5 мм.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕМЕНТА НАЗНАЧЕНИЯ ВЕСА С ЭКСЦЕНТРИЧНО ВРАЩАЮЩИМСЯ ЭКРАНОМ

Основной задачей математического моделирования ЭНВ является определение зависимости вносимых энергетических потерь в функции от угла поворота эксцентрично вращающегося экрана в зазоре между двумя ГЦЛ. Расчетная схема для получения математической модели приведена на рис. 2. Центр вращения экрана 1 совмещен с началом системы координат XOY и смещен относительно геометрического центра образующей окружности диска на величину эксцентриситета ε . При вращении вектора эксцентриситета относительно начала координат XOY за счет изменения координат центра диска y ₀ ′= ε sin α , x ′= ε cos α будет вращаться и сам диск 1.

При ε= R2 , α= 0 и R1> R2 экран полностью перекроет торец передающего ГЦЛ, что соответствует нулевому значению коэффициента пропускания ЭНВ. При α= 1800 экран полностью выйдет из области торца ГЦЛ, что соответствует единичному значению коэффициента пропускания ЭНВ. Таким образом, регулировка коэффициента передачи осуществляется в диапазоне изменения угла поворота диска от 0 до 1800.

Как видно из рис. 2, задача сводится к отысканию площади взаимного перекрытия S _{1 2} ( α ) областей градиентной линзы 2 и вращающегося круглого непрозрачного экрана 1:

S _1,2( α ) ∈ S ₁( α ) ∩ S ₂( α ) . (1)

Решение этой задачи аналитическими методами приводит к громоздким выражениям, неудобным для практического использования. Поэтому воспользуемся численным методом решения задачи. В этом случае для нахождения искомой площади достаточно вычислить число пикселей, формируемых координатной сеткой, одновременно принадлежащих области экрана

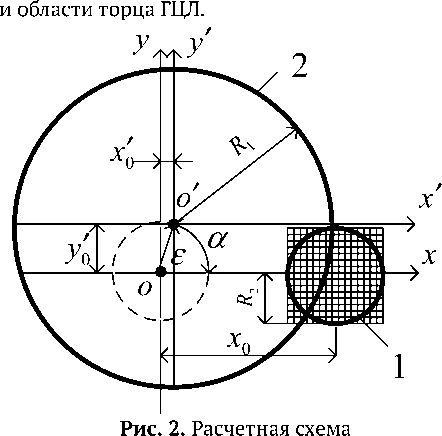
для получения математической модели

Уравнения образующих окружностей экрана (с учетом эксцентриситета) и торца ГЦЛ имеют вид:

(y - г sin a)2 + (x - г cos a)2 = R12, y2 + (x - x 0)2 = R 2.                  ()

Тогда условие принадлежности произвольной точки M ( x , y ) к области взаимного перекрытия областей можно представить в виде:

M ( x , y_} ) e S 1 ( a ) n S 2 ( a ) =

Уменьшение чувствительности обеспечивает более высокую точность установки весовых коэффициентов ЭНВ.

АЛГОРИТМ ПРОГРАММЫ ДЛЯ ПОЛУЧЕНИЯ И АНАЛИЗА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭЛЕМЕНТА НАЗНАЧЕНИЯ ВЕСА

Алгоритм программы, реализующей описанный способ получения и анализа математической модели ЭНВ приведен, на рисунке 3.

Исходными данными вычислитель- ного алгоритма являются константы

( yj - г sin a ) ² + ( xi - г cos a ) ² <  R 1² , y 2 + ⁽ x ^{- x} o ^{) 2} <  R 22 .

R, R2, г, Aa, Ax, Ay, к, 5 ,5,. Угол поворота 1      2                          x y экрана принимает дискретные значения:

Из рис. 2 также видно, что информативные области изменения аргументов не выходят за пределы:

Л Л 180

am = mAa, Aa =---, m = 0, n, m = m +1.

n

В начале задается начальное простран-

ственное положение экрана a ₀ = 0 ( m = 0 ),

A x = A y = 2 R ₂ .            (4)

при котором экран полностью перекрывает торец ГЦЛ и коэффициент передачи:

В этом случае искомую площадь можно выразить в виде суммы пикселей, принадлежащих области перекрытия:

G (0) = 1 -

S (0) n R ₂ ²

n R ₂ ²

n R ₂ ²

= 0 .

nn

S ( a ) = 2Z N «^s 0 ,        (5)

i = 0 j = 0

где N_ij – число пикселей, принадлежащих области перекрытия, S ₀ - площадь одного пикселя размером 5 _xi • 5 y .

Значения 5 _xi и 5 y определяются шагом координатной сетки:

„   Ax  Ay

• = 5 . = — = — xi yj kk,

где k – целое число, выбираемое, исходя из требуемой точности вычислений.

По полученному значению S(a) можно зависимость коэффициента передачи ЭНВ при по- вороте экрана:

G (a) = 1 - S^, а также оценить скорость изменения коэффициента передачи ЭНВ по углу поворота:

т ( a ) = dG a . d a

Учитывая, что угол поворота экрана связан с углом поворота вала червячной передачи соф отношением a = —, где к коэффициент редук-k ции угла червяной пары, то чувствительность коэффициента передачи излучения к изменению угла ф будет меньше чувствительности по углу a за счет уменьшения в к раз масштаба по оси a.

Затем задается первое дискретное положение экрана, равное a 1 = A a при m = 1 . В этом положении задается номер столбца локальной координатной сетки (рис. 2) i = 0 . После этого вычисляются координаты j -тых пикселей, принадлежащих нулевому столбцу координатной сетки:

2 R x^ = (x0 - R2) + i5x, 5x = —2, г = 0, ik yj = -R2 + j5y, 5y = jRj-, j = j +1, j = 0, к. k

Далее проверяется принадлежность пикселей с координатами x ₀, y j к области перекрытия экрана и торца ГЦЛ в соответствии с условием (3). Изменяя индекс j в диапазоне j = 0, к , j = j + 1 определяем число пикселей j -го столбца N ₀ j , принадлежащих искомой области. Площадь перекрытия S ( A a ) будет равна:

S 0,j = N 0,j S 0

^, где S ₀ = 5 _x 5 _y - площадь одного пикселя.

Найденное значение S₀ j записывается в память ПК. Аналогичным образом анализируется принадлежность пикселей области перекрытия пр и и зменении номера столбца в диапазоне i = 1, к , i = i + 1 Общая площадь перекрытия равна сумме:

kk

S ( A a ) = ££ N_y ( A a ) S 0 .

i = 0 j = 0

Полученное значение S ( A a ) записывается память ПК. После этого задается следующее

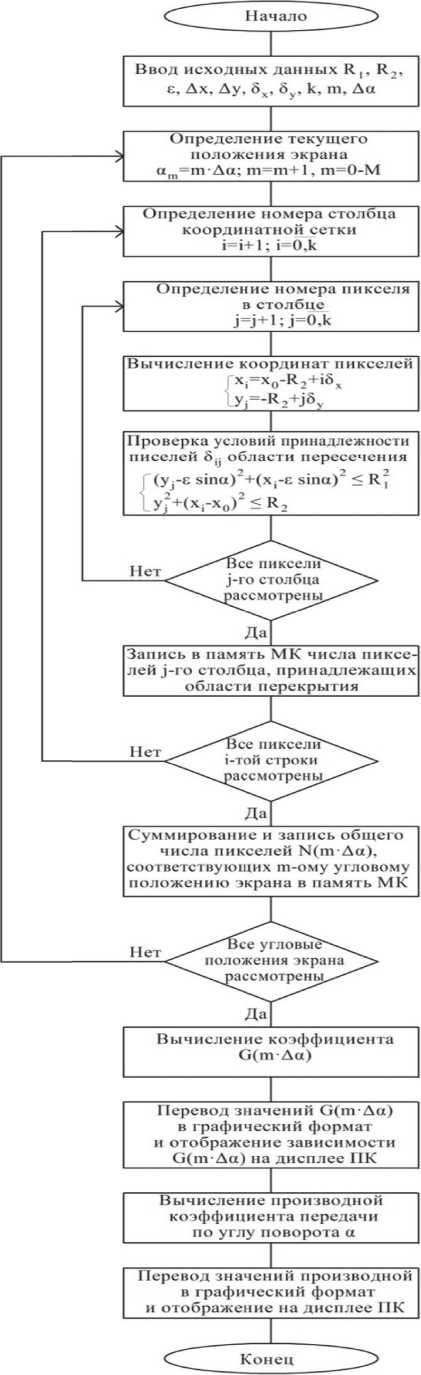
Рис. 3. Алгоритм программы, реализующей способ получения и анализа математической модели ЭНВ

дискретное значение угла поворота экрана а = 2 А а и в соответствии с описанной процедурой вычисляется второе значение площади S (2 А а ) при т = 2 . При изменении угла поворота в диапазоне 0-180° с шагом Аа , в памяти ПК сформируется числовой массив из n значений площадей перекрытия, соответствующий всем дискретным значениям угла поворота. Значение коэффициента передачи ЭНВ для m

-го значения угла поворота экрана вычисляется по формуле:

G ( а _т ) =

S ( а т ) n R 22

.

Полученные данные переводятся в графический формат и отображаются на экране дисплея в виде зависимости G(ат ). С использованием полученного числового массива вычисляются значения чувствительности коэффициента передачи ЭНВ к изменению угла поворота т +1) Аа] - G (тАа)

Аа          ’

которые также отображаются на дисплее в виде графика T( а _т ) (рис. 4).

По расчетным графикам, представленным на рисунке 4, видно, что наиболее неблагоприятный участок – это точка перегиба производной, где крутизна коэффициента передачи максимальна. Как следует из проведенного расчета, на интервале от 87,5 градусов до 92,5 градусов приращение коэффициента передачи равно 0,0227, что в пересчете на 1 градус составляет 0,0045, а с учетом коэффициента редукции 9,9 * 10 ^{- 5} . На всех остальных участках, где характеристика носит более пологий характер, приращение коэффициента передачи на единицу угла поворота вала червяка будет еще меньше, а следовательно, описанная конструкция позволяет добиться точной регулировки коэффициента передачи излучения между ГЦЛ, погрешность его установки составит не более 0,01%.

ЗАКЛЮЧЕНИЕ

Впервые предложена оригинальная конструкция регулируемого ЭНВ ВОЦАП с эксцентрично вращающимся круглым экраном в зазоре между передающим и приемным световодами. Получена математическая модель указанного ЭНВ с помощью численных методов. На основе математической модели разработан алгоритм программы для получения и анализа математической модели элемента назначения веса. Использование данной программы позволило получать зависимости коэффициента передачи ЭНВ от угла поворота экрана и чувствительности ЭНВ к изменению угла поворота.

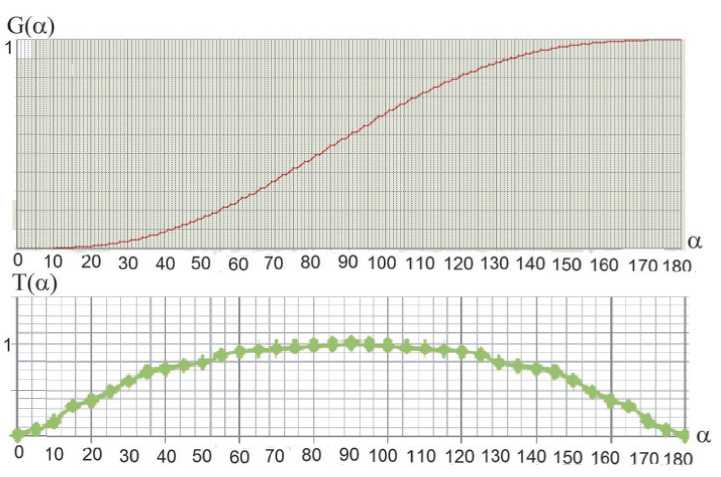
Рис. 4. График зависимости коэффициента передачи ЭНВ от угла поворота экрана и чувствительности коэффициента передачи ЭНВ к изменению угла поворота

Показано, что поворот вала червячной пары на 1 ° приводит к изменению коэффициента передачи на 10 4 , что соответствует требованиям к погрешности установки весового коэффициента в младшем разряде 14-ти разрядного ЦАП.