Регулятор тока с цифровым управлением

Регуляторы тока предназначены для обеспечения нагрузки током, который не зависит от выходного напряжения источника и регулируется только управляющим сигналом. Такие регуляторы применяются в измерительных схемах, например, при измерении сопротивления, для управления моментными электродвигателями, соленоидами и др. Поскольку в настоящее время большинство электронных устройств содержит микроконтроллеры (МК), а многие МК, даже недорогие, включают аналого-цифровые и цифро-аналоговые преобразователи (соответственно, АЦП и ЦАП), то становится целесообразным управление регулятором тока от МК.

При проектировании регулятора тока с цифровыми обратными связями необходимо обеспечить надлежащие качество регулирования и запасы устойчивости, в том числе и в условиях больших возмущений.

Регулятор тока

Блок-схема регулятора тока представлена на рис. 1. Здесь обозначено: МК – микроконтроллер, ЦАП – цифро-аналоговый преобразователь, АЦП – аналого-цифровой преобразователь, УМ – усилитель мощности, в качестве которого в случае однонаправленного выходного тока может быть применен эмиттерный или истоковый повторитель, ДТ – датчик тока, R , L – соответственно, сопротивление и индуктивность нагрузки.

Процессы в нагрузке описываются уравнением

Ldit ) + i ( t ) R = u ( t ).                        (1)

dt

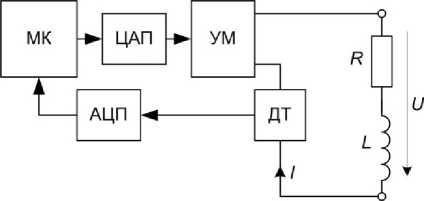
Рис. 1

Структурная схема системы приведена на рис. 2. Здесь обозначено: Т – импульсные элементы с периодом дискретизации Т ; K С – коэффициент передачи датчика тока; т = L / R - постоянная времени цепи нагрузки; блок с передаточной функцией (1 - e ^{- sT} )/ sT – экстраполятор нулевого порядка, отображающий ЦАП, который фиксирует на протяжении вычислительного цикла микроконтроллера Т аналоговый выходной сигнал; W ^* _к ф ( z ) – дискретная передаточная функция корректирующего фильтра, реализуемая программой МК; I _э – эталонный (заданный) ток.

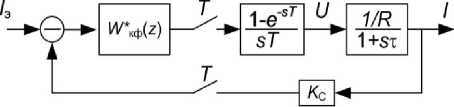
Рис. 2

Синтез корректирующего фильтра

Найдем z-преобразование непрерывной части системы. Согласно [1], дискретная передаточная функция непрерывного объекта с экстраполятором нулевого порядка

W * ( z ) = — z ( Ws) 1 = KC 1 - d ,      (2)

z [ sR z - d

где W ( s ) = K С / R (1 + s т ) - передаточная функция непрерывной части системы, d = e ^- T ^{/ т} .

Для того чтобы обеспечить нулевую статическую ошибку и конечное время переходных процессов, требуется [1], чтобы передаточная функ-

ция системы в замкнутом состоянии

Ф * ( z )

W * ( z ) W ^( z )

1 + W * ( z ) W ^( z )

- 1 = z ,

откуда дискретная передаточная функция корректирующего фильтра с учетом (2)

W * ( z ) = —.                (4)

^кф      K _C (1 - d )( z - 1)

Определим запас устойчивости по коэффициенту усиления корректирующего фильтра. Пусть

W * ( z ) = A — .              (5)

^кф        K _C (1 - d )( z - 1)

Характеристическое уравнение системы с учетом (5)

A

W * (z )W^( z) +1 = —- +1 = 0.(6)

z - 1

Условие устойчивости

|z| < 1,(7)

откуда с учетом (6) следует:

0 < A < 2.(8)

Сравнивая (4) и (5), убеждаемся, что запас устойчивости по усилению равен 6 дБ, что вполне достаточно.

Запас устойчивости по фазе найдем, анализируя частотную характеристику (ЧХ) разомкнутой системы при z = exp(—' ш Т ):

W раз ( j ®) = W* ( j®)W кф ( j ®) = --^-.     (9)

e* -1

Модуль ЧХ при частоте, равной частоте среза, равен единице:

ej ^- ср T - 1

= 1,

откуда

Ш ср = п / Т .                                    (11)

1         2п arg Wраз(j-cp) = arg en/3 - 1 = -у = -120°. (12)

Таким образом, запас устойчивости по фазе составляет 60 ° , что также достаточно.

Влияние нелинейности

Приведенные выше результаты справедливы для режимов малых возмущений, при которых регулятор тока ведет себя как линейная система. В случае же глубоких возмущений, например, при пуске, проявляются нелинейные свойства регулятора тока, обусловленные ограничением выходного напряжения усилителя мощности. Для оценки влияния этих возмущений проведем моделирование системы в пакете VisSim . Схема моделирования приведена на рис. 3. Здесь обозначено: НЭ – нелинейный элемент, ограничивающий выходное напряжение корректирующего фильтра пределами 0 <  u ( t ) <  U M . Модель нагрузки, соответствующая уравнению (1), находится в правой части рис. 3 и представлена блоками масштабирования 1/ L и R , а также интегратором и сумматором.

Рассмотрим пример моделирования системы с параметрами: L = 0,1 Гн, R = 0,2 Ом, K C = 0,05 Ом, U M = 15 В, T = 0,0002 с. На рис. 4 представлены графики изменения тока и напряжения при пуске регулятора тока с I э = 0,2 А. В начале процесса ошибка регулирования ε очень велика, поэтому напряжение на выходе УМ максимально. Система разомкнута. При переходе в линейный режим система замыкается и переходный процесс заканчивается за один такт T , т. е. система является оптимальной по быстродействию в классе цифровых систем с периодом дискретизации Т .

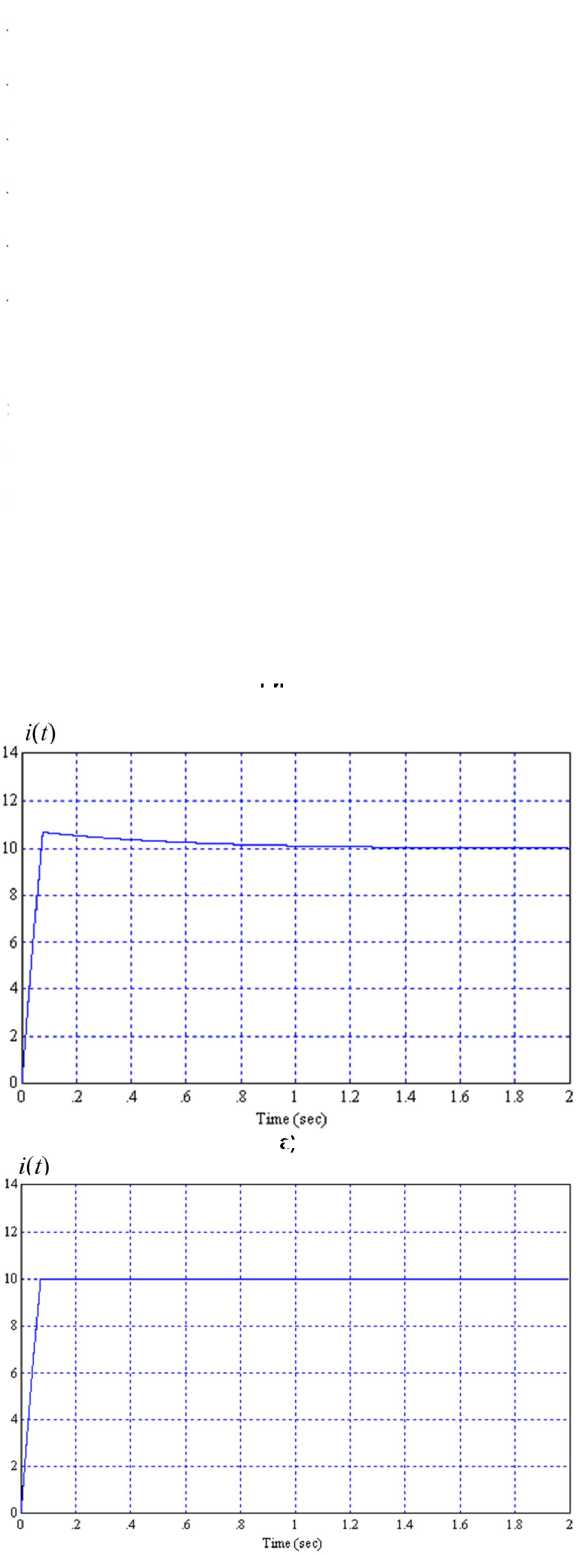
На рис. 5, а приведен график изменения тока при пуске регулятора тока с I э = 10 А. Здесь после нарастания тока до заданного значения возникает длительный переходный процесс, обусловленный тем, что операция интегрирования, которая входит в алгоритм корректирующего фильтра, накапливает в течение длительного времени ошибку ε, достигающую очень большой величины. При восста-

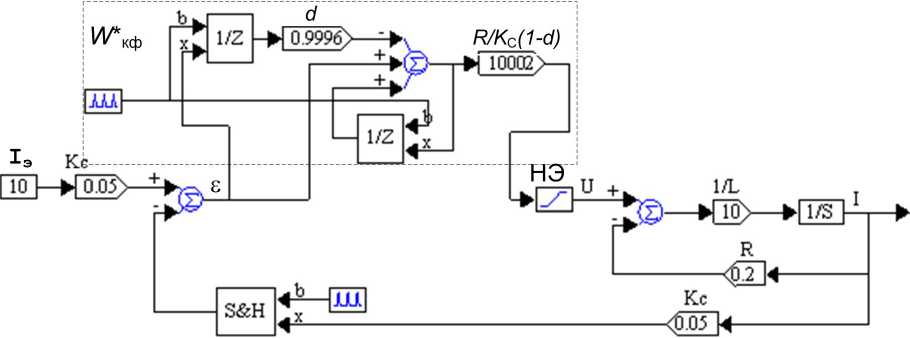
Рис. 3

Волович Г.И., Яковлев В.А.

Регулятор тока с цифровым управлением

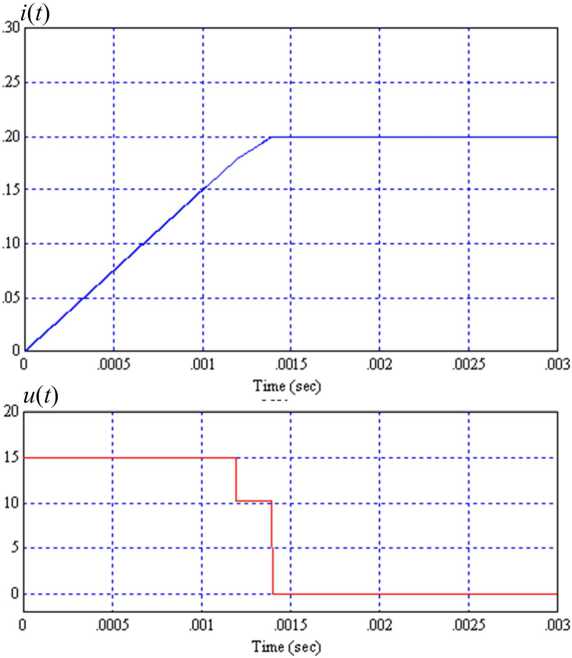
Рис. 4

а)

б)

Рис. 5

новлении линейного режима на переход интегратора в состояние, соответствующее этому режиму, требуется значительное время.

Одним из путей устранения этого дополнительного переходного процесса может быть программное ограничение максимального значения ошибки ε величиной, равной

,         K C ( 1 - d )

^ъ M = U M    _n

На рис. 5, б показано, что введение ограничения на сигнал ошибки, вычисленного по формуле (13), обеспечивает окончание переходного процесса при достижении заданного значения тока за один такт и при больших токах.