Рекомендации по применению ряда критериев проверки отклонения распределения вероятностей от нормального закона в практике инженерного статистического анализа

Нормальный закон распределения вероятностей случайных величин занимает центральное место как в классической математической статистике, так и в практических приложениях. Полнота теоретических исследований, относящихся к нормальному закону, а также его сравнительно простые математические свойства делает его наиболее привлекательным и удобным в применении. Широкое его использование связано в первую очередь с центральной предельной теоремой. Действительно, в самых различных областях наблюдается суммарный аддитивный эффект большого количества независимых факторов, приводящий к нормальному распределению отклика. Даже в случае отклонения исследуемых экспериментальных данных

от нормального закона существует по крайней мере два пути его целесообразного использования: использовать его в качестве первого приближения, что достаточно часто дает приемлемые практические результаты или подобрать нормализующее преобразование, например, преобразование Джонсона [1-3]. Удобным для статистического анализа является и свойство «самовоспроизводимости» нормального закона, заключающееся в том, что сумма нормально распределенных случайных величин также подчиняется нормальному закону. Кроме того, с помощью нормального распределения выведен ряд других важных распределений, построены различные статистические критерии и пр. (например, χ² , t и F -распределения и опирающиеся на них критерии).

Именно поэтому проверка возможности описания распределения экспериментальных данных нормальным законом распределения занимает центральное место в комплексе алгоритмов обработки измерительной информации.

В случае принятия гипотезы нормальности используются эффективные параметрические ал- горитмы обработки измерительной информации, так же как алгоритмы выявления аномальных измерений, фильтрации, допускового контроля, оценки соответствия вероятностных показателей качества продукции предъявляемым требованиям и пр. При отклонении гипотезы нормальности обычно переходят на алгоритмы непараметрической статистики, не зависящие от вида закона распределения, однако требующие существенно большего объема выборок.

Вообще говоря, все критерии согласия, позволяющие исследовать вид распределения вероятности, могут быть использованы для проверки нормальности. Однако рассмотренные ниже критерии специально приспособлены для этого частного случая и имеют наибольшую мощность по сравнению с универсальными критериями согласия.

• 1.    КЛАССИФИКАЦИЯ КРИТЕРИЕВ ПРОВЕРКИ НОРМАЛЬНОСТИ

Соответствующие критерии проверки нормальности, называемые иногда критериями Романовского, имеют вид

I b - m

ri-a/i;J---------d ^ иi-/i, (3)

° b 2

I d - m d\         v b \_<п

^J ^ и .-/I ; V^ ^U i

° d              ° b

где md, m^ , о d, о b., о b2 - соответственно математические ожидания и средне-квадратические отклонения выборочных оценок d, Tb!, b2 ; U1-a/2 - квантиль стандартного нормального распределения уровня 1 - а2.

Процентные точки ^d a/2 ' ^d 1 - a/2 ' ^Ь 1 ( 1 - ^2 ) ^{, Ь} 2 a/2 ' ^Ь 2 ( 1 - a/2 ) приведены в таблицах [4] при различных n и а .

Так как значения моментных отношений (1) могут иметь место и для распределений, отличных от нормального, то близость теоретических и выборочных значений не обязательно сви- детельствует о нормальности теоретического распределения. Поэтому критерии (3) служат главным образом для выявления отклонения

Параметрические критерии основаны на использовании свойств оценок моментов распределений [4,5].

При этом вычисляются выборочные оценки:

- математического ожидания x =

n

¹ Z X i ; n i = 1

• -  дисперсии S² = 1 £ ( x - _x ) ²

n i = 1

или S ² = J- У ( x - x )²;

• ¹    n - 1 ^{Z (} i ) ^;

  - нормированного среднего абсолютного отклонения d = — Z. I x - x |;

nS t1' '

от нормальности, т.е. для проверки гипотез d Ф ^ 2/л ; д/р . Ф 0 ; р₂ ф 3 Карл Пирсон показал, что распределение статистики ^Ь_х довольно быстро приближается к нормальному, тогда как распределение b ₂ даже при больших n оказывается далеким от нормального. Роберт Гири предложил заменить критерий b ₂ критерием , так как распределение статистики d удовлетво-

1 ⁿ

- показателя асимметрии bb = = —Z( x - x ) ;

рительно аппроксимируется нормальным при n >  50 .

При объемах выборки n >  50 статистики ^bbi и b ₂ приближенно имеют распределения V b 1 ~ N ( 0;6/ n ) ; b ₂ ~ N ( 3;24/ n ) , на основе которых строится критерий Крамера.

Чтобы избежать двумерности задачи при использовании статистик д/ Ь ^ и b ₂ в [5] рассмотрена совместная статистика

- показателя эксцесса b2 =    Z (xi- x )4, nS ,=1

где x i - измеренное значение случайной величины; n - объем выборки.

Для нормального закона распределения ис

(V b 1 ) ⁿ n ( b₂ - 3 ) ²

6        24

тинные значения этих характеристик равны d = Т2Д ; в = 0; р2 = 3,         (1)

выборочные оценки асимптотически нормаль-

ны с параметрами [4]

d n 1 /1 [,+_2_

V л L 8 n - 9

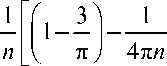
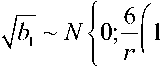
12 А

2 n + 7 )

n

b ₂

N 13 -

6 24 L 255 А

---------------;--------- I 1-- I n - 1 n V 15 n + 124 )

которая асимптотически распределена как ^-распределение. Однако, т.к. составляющей совместной статистики является b ₂ -стати-стика, совместная статистика плохо сходится к асимптотическому распределению и ее не рекомендуется использовать для выборок малого объема.

На практике из данной группы критериев наиболее часто применяется критерий, основанный на статистике d (называемый иногда критерием Гири) и критерий Крамера. Принятое при этом решение о ненормальности исследуемого распределения не требует дальнейшего уточнения, в то время, как решение о нормальности может быть уточнено на основе более мощных критериев.

Критерии основанные на сравнении параметрических и непараметрических выборочных оценок [5-7,15]. Критерий Шапиро-Уилка [5,7,15] базируется на сравнении линейной комбинации разностей порядковых статистик

T =

{ ( C n u ) ^- ' "°

+ g -^{( n - 1 )}} n ^{- 1} ,

b = «

k

^_a a n - i + 1 [ x ( n - 1 + 1 ) i = 1

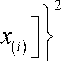
где k = n 2 - для четных n ; k = ( n - 1 ) /2 - для нечетных n ; и параметрической оценки

n

S2 • n=E( x- x )2, i =1

1                  d где Cn = —(n!)n-1; g = i( . .

2 n             ( nn - 1 ) n

Гипотезы нормальности отклоняются при больших значениях статистики T . Процентные точки также табулированы [6]. Там же анализируются ограничения, затрудняющие использо-

где x ( 1 ) < .. . <  x ( i ) < . . <  x ( _n ) - порядковые статистики, а коэффициенты a n _ i _{+ 1} , табулированы для n <  50 [7,15].

вания данного критерия.

Критерий Эппса-Палли основан на сравнении характеристических функций выборочных данных и нормального распределения [5,7]. Статистика критерия вычисляется по формуле

Гипотеза о нормальности принимается при больших значениях статистики W = b ²/( S ² • n ) . Процентные точки статистики W табулирова-

и Э n k - 1

T™ = 1 + 4 + ² 2Z exp j

^-( x j ^- xk ^{) 2} , 2 5²

ны, начиная с n = 3 [5,7,15].

При больших объемах выборки n >  50 используется приближенный критерий Шапиро-Франчиа, в котором вместо табулированных коэффициентов a n _ i _{+ 1} используются выражения

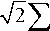
j = 1

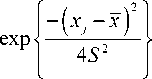
a

m

n - i + 1

n - i + 1

n m2 i,

V i = 1

12 ,

где m _{i , n} – математическое ожидание i -й порядковой статистики стандартного нормального

распределения

m i, n = ^{ф 1}

f . 3 ) г — ——

n + -

V 4 J

при p =

. 3 г — -8-.

1 ^, n +

Гипотеза нормальности принимается при больших значениях этого критерия. Вычисления критерия достаточно сложны и осуществляются в соответствии с алгоритмом приведенном в ГОСТ Р ИСО 5479-2003 [7]. Там же приведены процентные точки.

Критерий применим при n >  8 и является сильным конкурентом критерия Шапиро-Уилка. Заметим однако, что характеристические функции не являются привычным инженерным методом.

Критерии, базирующиеся на сравнении нормального распределения и эмпирических функций распределения выборочных данных [4,6] . Статистика критерия Фросини [6] имеет вид:

Ф–1 – обратная функция стандартного нормального распределения.

Для упрощения нахождения обратной функции Ф–1 можно использовать аппроксимацию

U p = 4,91 [ p⁰¹⁴ - ( 1 - p ) ^0,14 ] .

Близким к критерию Шапиро-Уилка является критерий Дэйвида-Хартли-Пирсона, основанный на сравнении размаха выборки с оценкой средне-квадратического отклонения [4]

u = r/ S1 , где r = x(n)- x(1); S12

n - 1

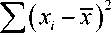
не- i=1

смещенная оценка дисперсии.

Процентные точки статистики u приведены в [6].

Комбинированный критерий Шпигельхаль-тера [6] базируется на комбинации статистики критериев Гири и Дэйвида-Хартли-Пирсона [6] и имеет вид

B n

i — 0,5

n где z(i) =( xi - x)^S - центрированные и нормированные случайные величины, упорядоченные по возрастанию.

Процентные точки статистики B_n табулированы [6]. Основным недостатком критерия Фросини является отклонение от нормальности случайных величин z ( i ) при небольших объемах выборки , за счет возникающих погрешностей оценок x и S .

От этого недостатка свободен критерий Хе-гази-Грина [6] со статистиками:

n                                     n ,              X 2

T1 = й ^ ZZ(^ - Ч" । , T2 = й ^ (Z(i) - 4 ) , где n 1 =1                    n 1=1

z ( i ) = ( ^x ( i ) ^- x )/ S t , П , = ^ф - ^{1 (} if ⁽ n + ^{1 ) )} , i] ( ⁿ + 1 ) – несмещенная оценка вероятности, соответствующей i -ой порядковой статистики z ( i ).

Здесь, в отличие от критерия Фросини, сравниваются не вероятности, а случайные величины, соответствующие этим вероятностям.

Известен также критерий Саркади [4], представляющий собой модификацию известного критерия согласия ю ² для проверки нормальности распределения [4]. В этом критерии путем проведения ряда преобразований также уда е тся исключить зависимость от точности оценок x и S ².

Формируются центрированные случайные величины

^0 = x (м) ^- ^П^ ⁽ x ' ^ ⁺ x ( ■ ) ) ,

или

Ч i ) = x ( i ) ^- j,^ ⁽ x • V n + x ( , > ) , i = 1, - , n - 1 .

Далее формируются нормированные случайные величины

/ 1 2 . . 2

V n - i - 1 ^{( 4} ( i + i ) ⁺•••⁺Ч n -o ) , i = 1, - , ^{n - 2} .

При гипотезе нормальности величины ^ i имеют t -распределение Стьюдента с ( n - i - 1 ) степенями свободы.

Значения функции распределения 5 ( i ) = t¹ ( ^ ( i ) ) , где t ^-1 - обратная функция t -распределения, равномерно распределены на интервале [ 0,1 ] .

Проверка нормальности осуществляется по ю ²-критерию, процентные точки соответствующей статистики табулированы [4]:

( n - 2 ) to ²

12(n - 2)

n - 2

+X

i = 1

5n

2 i - 1

2 (n - 2)

Есть данные, что критерий Саркади применим для выборок малого объема n >  3.

2. ПРОБЛЕМЫ СРАВНЕНИЯ КРИТЕРИЕВ ПРОВЕРКИ ОТКЛОНЕНИЯ РАСПРЕДЕЛЕНИЙ ОТ НОРМАЛЬНОГО ЗАКОНА

Все критерии согласия, как классические, так и проверки отклонения распределений от нормального закона относятся к так называемым критериям значимости, базирующихся на ряде общих принципов [8-10]:

• -    выбирается исследуемая статистика;

• -    определяется теоретическое распределение данной статистики, соответствующее проверяемой нулевой гипотезе (в данном конкретном случае – гипотезе о нормальности);

• -    выбираются значения малых с точки зрения исследователя вероятностей, ограничивающих критическую область (выбор уровня значимости);

• -    если экспериментальные значения статистики попадают в критическую область, то в соответствии с принципом практической не-

возможности осуществления маловероятного события, нулевая гипотеза отвергается; в противоположном случае считается, что полученные экспериментальные данные не противоречат нулевой гипотезе и последняя принимается.

Заметим, что утверждение «нулевая гипотеза не верна» более категорично, чем «экспериментальные данные не противоречат нулевой гипотезе».

Для расчета мощности критериев значимости необходимо задать альтернативную гипотезу. При проверке нормальности распределений задание альтернативной гипотезы затруднительно.

Действительно, если исследуемое распределение не подчиняется нормальному закону распределения, то какому из множества законов распределения оно подчиняетя? Перебирать все возможные распределения невозможно.

В [5, 6] в качестве альтернативных гипотез рассмотрено 3 распределения, в том числе семейство распределений Лапласа и логистическое распределение, что снижает практическую ценность проведенных исследований.

Процентные точки, приведенные в работах [47] рассчитаны при условии нормальности исследуемого распределения. Каждой из альтернативных гипотез будет соответствовать другое распределение используемых статистик. При этом вывести аналитическое выражение этих альтернативных распределений чрезвычайно сложно и единственно возможным методом расчета мощности сравниваемых критериев является статистическое моделирование достаточно большого объема, что также затруднительно в инженерной практике.

В данной работе предлагается другой подход к сравнению критериев, основанный на логике функционирования критериев значимости.

3. ВОЗМОЖНЫЕ ПОДХОДЫ К РЕШЕНИЮ ЗАДАЧИ СРАВНЕНИЯ РЯДА КРИТЕРИЕВ СОГЛАСИЯ С НОРМАЛЬНЫМ ЗАКОНОМ

РАСПРЕДЕЛЕНИЯ

Авторы не ставили перед собой объемной задачи сравнения всех перечисленных критериев согласия, а только более скромную задачу иллюстрации предлагаемых подходов на примере исследования отдельных представителей каждого класса критериев.

Рассмотренные выше особенности приведенных критериев проверки нормальности позволяют выделить из каждой группы критериев критерии, наиболее удобные для практического использования. Кроме того, необходимо учитывать, что проблема проверки нормальности распределения наиболее остро стоит для малых выборок, характерных для испытаний сложных технических систем, например систем летательных аппаратов [8-10].

Действительно, из теории порядковых статистик известно [9], что доля произвольного распределения R , заключенного между минимальным x(1) и максимальным x(n) значениями, с доверительной вероятностью у составляет nRn - -(n -1) Rn = 1 - у.

Например, при n = 20 эта доля составляет при у = 0,9 всего лишь R ® 0,785 .

Таким образом, из общей функции распределения [ 0,1 ] для проверки нормальности «вырезается» фрагмент R = 0,785 . Естественно, по такому небольшому фрагменту различить распределения чрезвычайно сложно. Именно поэтому нулевой гипотезе соответствует не решение «эмпирическая функция распределения соответствует нормальному закону», а более осторожное решение «эмпирическая функция распределения не противоречит нормальному закону».

Исходя из всего вышеперечисленного для сравнения выбираем:

• -    из 1-й группы параметрических критериев – критерий Гири;

• -    из 2-й группы – критерии Шапиро-Уилка и Дэйвида-Хартли-Пирсона;

• -    из 3-й группы – критерии Хегази-Грина 1 и 2.

Проведено тестовое статистическое моделирование при выборе в качестве эталонного распределения – стандартного нормального распределения с нулевым математическим ожиданием и единичной дисперсией. Объем моделирования составил 10 выборок по 20 реализаций в каждой. Решение о предпочтительности того или иного критерия принималось на основе сравнения при использовании двух основных подходов: математико-статистического и экспертно-статистического.

Математико-статистический подход. Сравнение критериев ведется с использованием аппарата математической статистики. В соответствии с принципом применения критериев значимости уровень значимости а определяет размер критической области отклонения проверяемой (нулевой) гипотезы H ₀. При этом малым значениям уровня значимости соответствует малый размер критической области, т.е. область принятия нулевой гипотезы расширяется. В пределе, при а ^ 0, любые экспериментальные данные считаются не противоречащими нулевой гипотезе. Естественно степень доверия к такому решению мало. В [8-13] введено понятие критического уровня значимости, по аналогии с критической областью, – это граничный уровень значимости, при котором еще может быть принята нулевая гипотеза. При правосторонней критической области:

% = F (0 > 6ЭКс) = 1 - F (баке H) );

Кр                   ЭКС.                    ЭКС. V при левосторонней критической области:

% = F ( 6 <  0 . 1 F ( 0_ЭКС ./ Н о ) ;

для двусторонних критериев:

« кр = 2 min [ F ( 0_JH , ) ;1 - F ( 0 ЭКС./ Н , ) ] , где 9 _экс - значение статистики, вычисленное по выборке; F – функция распределения вероятности статистики 9 .

В [14] используется аналогичный термин – достигнутый уровень значимости. При больших значениях критического уровня значимости экспериментальные данные близки к ожидаемым теоретическим результатам, соответствующим нулевой гипотезе и наоборот. Данный подход был использован в задачах оценки адекватности статистических математических моделей, в задачах оценки статистического подобия при объединении информации о показателях качества сложных технических систем, полученной на различных этапах их экспериментальной отработки [8-13]. Однако в этих задачах имели место типовые законы распределения вероятностей – биномиальный, нормальный, Стьюдента, Пирсона, Фишера.

Для этих законов имеются как программы расчета квантилей (процентных точек), включенные в пакеты прикладных программ по математической статистике, так и достаточно полные таблицы, представленные в многочисленных справочных изданиях, например в [4].

Попытки применить данный подход к решению сравнительного анализа критериев проверки нормальности распределений натолкнулась на отсутствие подробной информации для специфических распределений статистик исследуемых критериев согласия.

Исключением являются графики функций распределений соответствующих вероятностей, приведенные в [5, 6]. Однако, использование этих графиков для определения значений а _кр не позволяет получить достаточную точность.

Экспертно-статистический метод. Сравнение критериев ведется с использованием математического аппарата допускового измерительного контроля качества продукции.

Традиционная схема принятия решения о согласии/несогласии экспериментальных данных с нулевой гипотезой нормальности исследуемого распределения вероятностей состоит в сравнении рассчитанной статистики критерия с выбранной процентной точкой функции распределения этой статистики.

В допусковом контроле этой схеме соответствует модель контроля Тейлора [10,16].

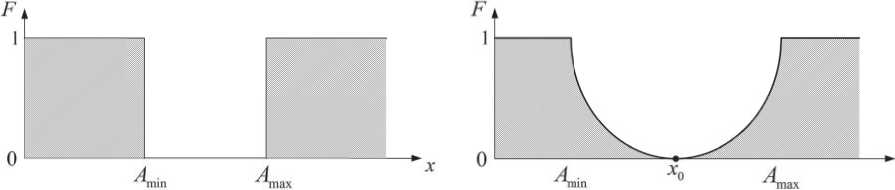
При использовании подхода Ф.У. Тейлора принято считать одинаково качественной всю продукцию, значения контролируемых параметров которой находятся внутри соответствующих допустимых интервалов. Потеря качества по Тейлору F _П иллюстрирует рис. 1а.

В основе подхода Г. Тагути лежит оценка качества по отклонению контролируемых параме- трое от середины допустимого интервала. При этом потеря качества оценивается функцией (рис. 1б):

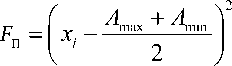
где A max и A min - нижний и верхний допустимые пределы; x i - значение измеряемого параметра; Х о = ( A m^ + A min )/2 - середина допустимого интервала.

Используется также приведенная величина потери качества:

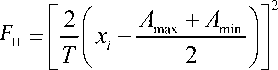
где T = A max — A min •

При x i = x ₀ потеря качества равна F _П = 0;

при Х = A min или Х = A max ^- F П = ¹

Применительно к решаемой задаче будем использовать:

• -    для правостороннего критерия (Хегази-Гри-на T 1 и T ₂) отсчет ведется от нуля, т.е. x ₀= 6 ₀= 0, T = ⁶ max , и имеем F = ( ⁶ ж ./⁶тах ) ² >^откуд^а при ⁶ зкс. = 0, F П = 0 (рис. 2а);

• -    для левостороннего критерия (Шапиро-Уилка) должны выполняться условия: 6 _экс= 1, F^ = 0; при 6 = 6 . , F^ = 1, т.е. примем х_п = 1 и П                  экс.     min , П ,                         0

^T -^{1 —} " min F = [ ( 1 — 6 _,)/( ! — 6 т,. ) ] (Рис. ^2б), где 6 _max, 6 _min - процентные точки статистик критерия для выбранного уровня значимости а , например, а = 0,01;

• -    для двустороннего критерия (Гири, Дэйви-да-Хартли-Пирсона):

„ _ [ ² (е_ - ⁶ ) 1 ²

Fn =      т       , где 60 - совпадает с медианой распределения статистики 6, T = 6max- 60 для 6экс > 60 или T = 60 - 6min для 6экс < 60 (рис. 2в). Здесь 60 - процентная точка статистик критерия при а/2.

а)                                                           б )

Рис. 1. Функции потери качества по Тейлору (а) и по Тагути (б)

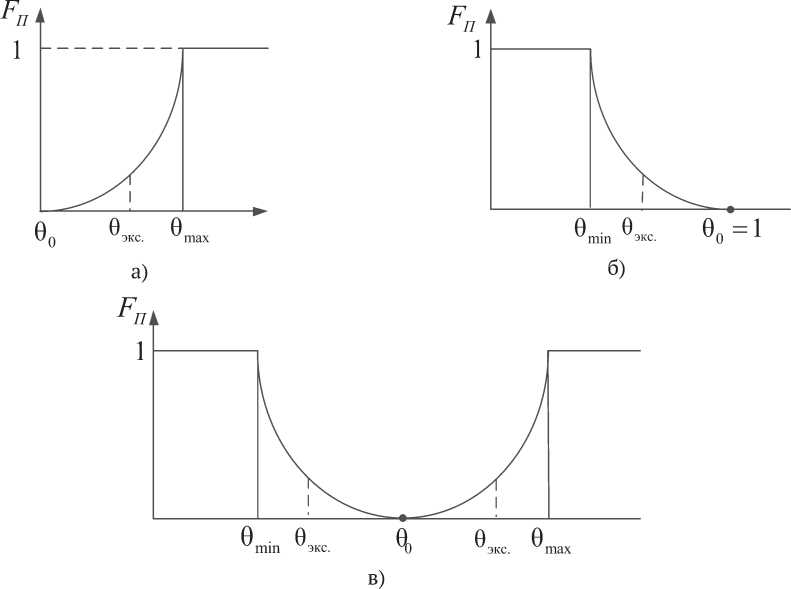
Рис. 2. Функция потерь Тагути для правостороннего (а), левостороннего (б) и двустороннего (в) критериев проверки нормальности

Таблица 1. Значения процентных точек ряда критериев проверки нормальности при объемах выборки n = 20 ; n = 40

Критерий		1 - a
		0,85	0,9	0,95	0,975	0,99
Гири	n = 20	0,741-0,870	0,790-0,878	0,713-0,889	0,697-0,899	0,644-0,91
	n = 40	0,754-0,848	0,747-0,854	0,735-0,863	0,724-0,871	0,71-0,879
Дэйвида-Хартли-Пирсона	n = 20	3,240-4,392	3,178-4,488	3,087-4,633	3,012-4,763	2,927 4,915
	n = 40	3,741-5,048	3,674-5,162	3,574-5,345	3,493-5,507	3,401 5,708
Хегази-Грина ( T )	n = 20	0,205	0,218	0,239	0,259	0,284
	n = 40	0,151	0,161	0,177	0,191	0,210
Хегази-Грина ( Т2 )	n = 20	0,072	0,082	0,100	0,118	0,143
	n = 40	0,043	0,049	0,060	0,070	0,085
Шапиро-Уилка	n = 20	0,925	0,92	0,905	0,875	0,868
	n = 40	0,955	0,949	0,94	0,925	0,919

В табл. 2 сведены результаты расчетов функции потери качества Тагути.

На основе анализа средних значений потерь качества по Тагути, представленных в табл. 2, может быть построен ряд предпочтений сравниваемых критериев согласия с нормальным законом распределения.

кр. Хегази-Грина (T 2 ) ^ кр. Гири ^ кр. Дэйвида-Хартли-Пирсона ^ кр. Шапиро-Уилка ^ кр. Хегази-Грина (T₁ ).

Предложенный подход не позволяет выявить степень предпочтения сравниваемых критериев для альтернативных гипотез существенно отличающихся от нормального закона распределения. Однако, практический опыт показал, что даже при существенных отличиях от нормальности, например, точностных характеристик автоматической посадки самолетов в полном диапазоне воздействия возмущающих случайных факторов в области вероятностей от 0,1-0,9, а иногда 0,05-0,95 эти законы приблизительно нормальны [3]. При этом проверка нормальности с применением соответствующих критериев носит, в основном, демонстрационный характер.

Пример 1. Подтвердить требования к вертикальной скорости самолета при касании его взлетно-посадочной полосы, заданные в форме

Pr { V <  V _max } = R₃

Таблица 2. Значения функции потери качества Тагути ряда критериев проверки нормальности при а = 0,01 и объеме выборки n = 20

№ п/п выборки Критерии проверки нормальности Гири Дэвида-Хартли-Пирсона Хегази-Грина (T1) Хегази-Грина ( T2 ) Шапиро-Уилка 1. 0,285 0,864 0,2 0,05 0,76 2. 0,239 0,216 0,23 0,07 0,69 3. 0,177 0,124 0,268 0,078 0,32 4. 0,013 0,044 0,286 0,099 0,21 5. 0,01 0 0,298 0,108 0,143 6. 0,03 0 0,341 0,122 0,106 7. 0,08 0,0016 0,358 0,137 0,092 8. 0,12 0,184 0,495 0,2 0,05 9. 0,159 0,263 0,67 0,213 0,045 10. 0,353 0,284 0,97 0,253 0,025 Средние значения функции потерь 0,147 0,186 0,41 0,133 0,244 с достоверной вероятностью у при следующих значениях Vmax = 1,5 м/с; R3 = 0,95; у = 0,9.

В математической постановке подтверждение требований в заданной форме сводится к построению одностороннего толерантного интервала и условию

X + kS < Vmax , где k > UR3 - индекс наблюдения, больший, чем квантиль стандартного нормального распределения UR и табулированный для нормального распределения вероятностей исследуемого параметра [18].

Таким образом, первым этапом процедуры подтверждения заданных требований является проверка гипотезы нормальности вертикальной скорости.

Исходные данные: n = 28 , x = 0,61 м/с, S = 0,413 , S 1 = 0,42 , имеется вариационный ряд измерений вертикальной скорости при проведении натурных испытаний в диапазоне 0,05 ^ 1,4 м/с.

В табл. 3 приведены результаты расчетов статистик ряда критериев и соответствующих потерь качества по Тагути при выборе уровня значимости а = 0,01.

ограниченном интервале вероятностей R <  0,95 по всем пяти критериям принимается решение о возможности использования нормального закона.

В том случае коэффициент k = 2,08 и с доверительной вероятностью у = 0,9 подтверждается значение V_max = 1,48 м/с.

ЗАКЛЮЧЕНИЕ

Современное понятие измерений определено как «алгоритмическая операция, которая данному наблюдаемому состоянию объекта, процесса, явления ставит в соответствие определенное обозначение: число, номер или символ» [17]. Под такое определение подпадают ординаты функции потери качества по Тагути.

Внедряемая в настоящее время в метрологию концепция неопределенности также расширяет понятие измерений, придавая большее значение различным экспертным методам [19,20]. В связи с этим, предложенный подход может быть включен в математическое обеспечение систем обработки измерительной информации. Его можно также рекомендовать для решения ряда задач, характеризующихся недостаточным объ-

Таблица 3. Расчетные статистики ряда критериев проверки нормальности распределения вероятности вертикальной скорости

	Критерии проверки нормальности
	Критерий Гири	Критерий Дэвида-Хартли-Пирсона	Критерий Хегази-Грина ( T )	Критерий Хегази-Грина ( T )	Критерий Шапиро-Уилка
Статистика критерия	0,806	3,2	0,245	0,093	0,9
Интервал принятия решения о нормальности	0,694-0,895	3,1-5,3	0-0,247	0-0,114	0,896-1
Значения функции потерь	0,012	0,826	0,975	0,665	0,924

Первые два места, как и при тестовом моделировании занимают критерии Хегази-Грина ( T 2 ) и Гири, причем здесь приоритет принадлежит критерию Гири. Ряд предпочтений остальных критериев сохраняется, как и при тестовом моделировании.

кр. Дэйвида-Хартли-Пирсона ^ кр. Шапиро-Уилка ^ кр. Хегази-Грина ( T )

В некоторых работах, например, в [9] есть данные, что распределение вертикальной скорости некоторых гражданских самолетов, например, Boing-737, описывается логарифми-чески-нормальным распределением. Однако в емом измерительной информации, например, для сравнения многочисленных методов выявления аномальных измерений, методов непараметрической статистики и пр., где затруднительно формулировать альтернативные гипотезы и использовать классический математический аппарат расчета мощности критериев.