Реконфигурация распределительных электрических сетей

В настоящее время цифровизация системы электроснабжения открывает новые возможности для повышения эффективности электропередачи распределения электрической энергии. В нормальном режиме работы распределительные электрические сети 6–10 кВ, имеющие разомкнутую структуру, секционированы таким образом, чтобы в аварийных или ремонтных режимах обеспечить бесперебойное электроснабжение потребителя.

Существующие технологии управления режимами в указанных электрических сетях не предполагают возможности изменения их топологии для обеспечения задач по снижению перегрузки и потерь электроэнергии в нормальных режимах. Как правило, задача оптимальной реконфигурации электрической сети возникает при восстановлении нормального режима после аварий, при перегрузке линий, при необходимости вывода электрооборудования в ремонт по критерию n – 1, при оптимизации режимов.

В данном исследовании рассмотрена реализация подходов к реконфигурации электрических схем в системе электроснабжения для обеспечения задач по стабилизации напряжений, снижению перегрузки и потерь электроэнергии в нормальных режимах. Задача по оптимизации структуры электрической сети при изменении активных и реактивных мощностей в последние годы широко прорабатывается в зарубежных и отечественных научных кругах.

В целом представленную задачу можно рассматривать как оптимизационную нелинейную смешанного целочисленного программирования [1, 2], которая решается большинством авторов методами, представленными на рис. 1.

Некоторые исследователи [3–6] придерживаются эвристических методов решения задачи оптимальной реконфигурации электрической сети, которые позволяют существенно уменьшить вычислительные и временные ресурсы, но получить приближенные решения. Оптимизационная задача комбинаторного типа решается авторами [7–9] с помощью алгоритмов салюта (фейерверка), нейронных сетей, нечетких множеств в основном в условиях ограниченной исходной информации.

Эвристические методы решения комбинаторных оптимизационных задач показали свою высокую эффективность в сравнении с классическими методами перебора при значительном количестве аргументов целевой функции, когда определяющим является не точность, а скорость вычислений. Методы оптимизации, связанные с поиском на графах, также находят все большее применение при решении задач поиска оптимальной топологии электрической сети в первую очередь из-за своей однозначной разрешимости [10, 11].

Хотя проблема минимального дерева в теории графов хорошо изучена [12], решение представленной задачи не является простым в силу того, что для построения оптимальной топологии необходимо не только минимизировать сопротивления линий распределительной сети, но и потери элек-

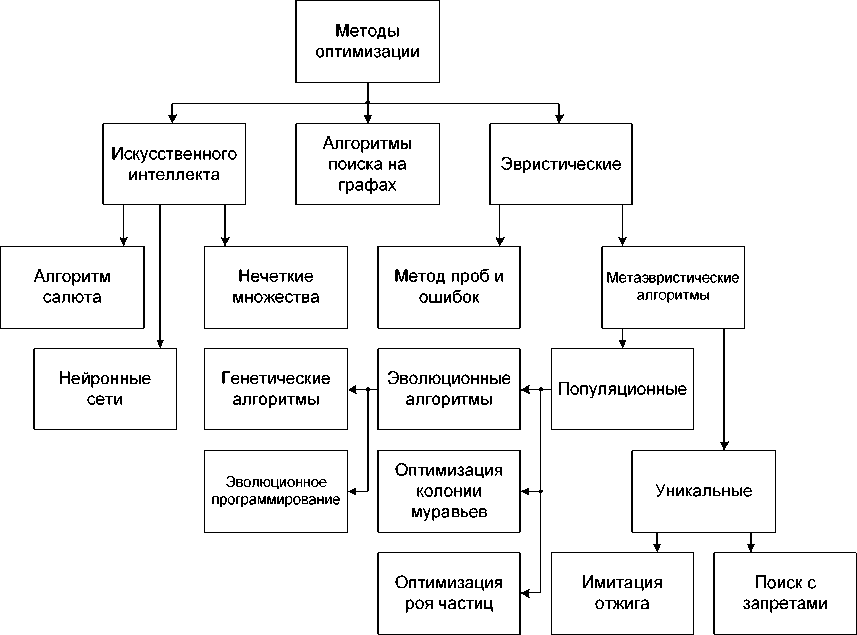
Рис. 1. Методы оптимизации для решения рассматриваемой задачи

троэнергии, определять потоки мощности для всех вариантов структуры сети, а также учитывать ограничения параметров режима и эксплуатации, надежность электроснабжения и прочее.

Постановка задачи

В данном исследовании предлагается решать задачу оптимальной реконфигурации радиальных электрических схем для ограничения перегрузки и снижения потерь электроэнергии. При этом в качестве критерия оптимизации топологии электрической сети выступает минимальное потребление электроэнергии при эксплуатационных ограничениях по схемам электроснабжения, допустимым параметрам режима, перегрузкам линий и т. д.

Теоретическая часть

Разомкнутые распределительные электрические сети 6–10 кВ (рис. 2) ограничены вариантами их реконфигурации по эксплуатационным режимам, обеспечения надежности и экономичности. Задача заключается в определении, какие из выключателей должны быть открыты для обеспечения наибольшего снижения электропотребления в электрической сети с заданными нагрузками.

Если для всех комбинационных вариантов положений выключателей выполнять полный расчет токораспределения и решать оптимизационную нелинейную задачу целочисленного программирования, это окажется неприемлемым для опе- ративного управления электрической сетью при перегрузке для снижения потерь электроэнергии. Поэтому целью данной работы является разработка более эффективных с точки зрения скорости и точности вычислений способов построения остов-ного графа электрической сети при рассматриваемой реконфигурации.

Для этого предлагается задачу реконфигурации разомкнутой распределительной электрической сети разбить на две подзадачи, как динамическую и статическую реконфигурацию, и решать их разными методами. Реконфигурация электрической сети для быстрого снятия перегрузки элементов осуществляется на основе агентного подхода методом ветвей и границ с использованием рекуррентных соотношений для определения потерь электроэнергии для всех участков без полного расчета установившегося режима. В нормальном режиме для выбора топологии электрической сети с минимальным потреблением и минимальными потерями электроэнергии решается нелинейная задача оптимизации установившихся режимов, имитирующих реконфигурацию, с учетом прогнозных значений нагрузок, взятых на основании типовых суточных графиков.

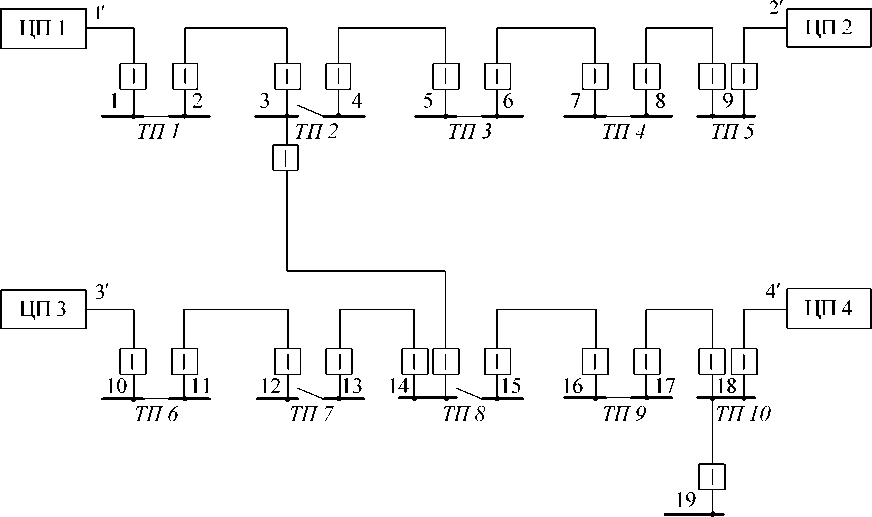
Представленную на рис. 2 распределительную электрическую сеть обозначим в виде графа G ( N ; E ), где N – шины: N = {1, 2, …, m }, а ( i , j ) ∈ E – линии (дуги, идущие от шины i к шине j ). Данный граф можно разбить на четыре подграфа (по числу

тп и

Рис. 2. Схема распределительной электрической сети 10 кВ

центров питания разомкнутой электрической сети): G 1 ( N 1 ; E 1 ), G 2 ( N 2 ; E 2 ), G 3 ( N 3 ; E 3 ), G 4 ( N 4 ; E 4 ). При этом N 1 ( i ) = { j ( i , j ) ∈ E }, N 2 ( i ) = { j ( j , i ) ∈ E } и т. д.

Модель потоков мощности для указанной радиальной электрической сети может быть представлена в виде:

P = I I sу(PHj-Pj) ■ 1 I 5W)

i e Nj e N ( i )                    i e Nj e N ( i )

Q = H 5 ij(Qj — QJ + I I 5 j(A Qij), W i E Nj E N (i)                     i E Nj E N (i)

Решение представленной оптимизационной задачи (2) методом ветвей и границ позволит получить значения двоичной переменной, которая описывает состояние ветви графа электрической сети: 0 – линия разомкнута, 1 – линия замкнута.

Определение потоков мощности выполняется без расчета установившегося режима по заданным инъекциям в узлах и топологии электрической сети. Допустимые параметры режима электрической сети по напряжению оцениваются по модулю

где P _{н j} , P _{г j} , и Q _{н j} , Q _{г j} – активные и реактивные

мощности нагрузки и инъекции на шине j ;

A P ij =

Pi2 + q2

_U 2 _j

■ r ij ,    ^A Q ij =

P j + Q j

_U 2 _j

■ x ij

потери

в конце линии на шине j по данным в начале линии на шине i в виде [13, 14]:

r P + x О i i x P — г О i

' ij¹! ⁺ x lJ Q l    ₊ x lj¹! ' iJ Q l      (4)

Ui   JI  Ui   J

^Uj =

U i

—

активной и реактивной мощности в линиях ij ; P ij , Q ij – перетоки активной и реактивной мощности в линиях ij ; r ij , x ij – активные и индуктивные сопротивления линий ij ; δ ij – двоичная переменная (δ ij = 0,1 ( i , j ) ∈ E ).

Для разомкнутой электрической сети с четырьмя центрами питания оптимизационная задача динамической реконфигурации на основе (1) может быть записана в виде:

Реконфигурация электрической сети для исключения перегрузки линий должна обеспечивать допустимый новый режим, если это возможно, иначе – прибегать к управлению спросом, вплоть

до отключения нагрузок.

Критерии реконфигурации:

- обеспечение баланса мощности, включая

P (5 ij )^ min

при ограничениях:

max ij ij ;

0 <  Q ij <  Q max ;

U m _j in

< U j <  U^mx.

резерв;

• -    исключение перегрузки электрооборудования;

• -    исключение недопустимых уровней напряжения и частоты;

• -    обеспечение требуемого уровня надежности электроснабжения;

• -    обеспечение требуемой частоты реконфигурации (порог).

Предлагаемый алгоритм рассматриваемой реконфигурации электрической сети представлен на рис. 3.

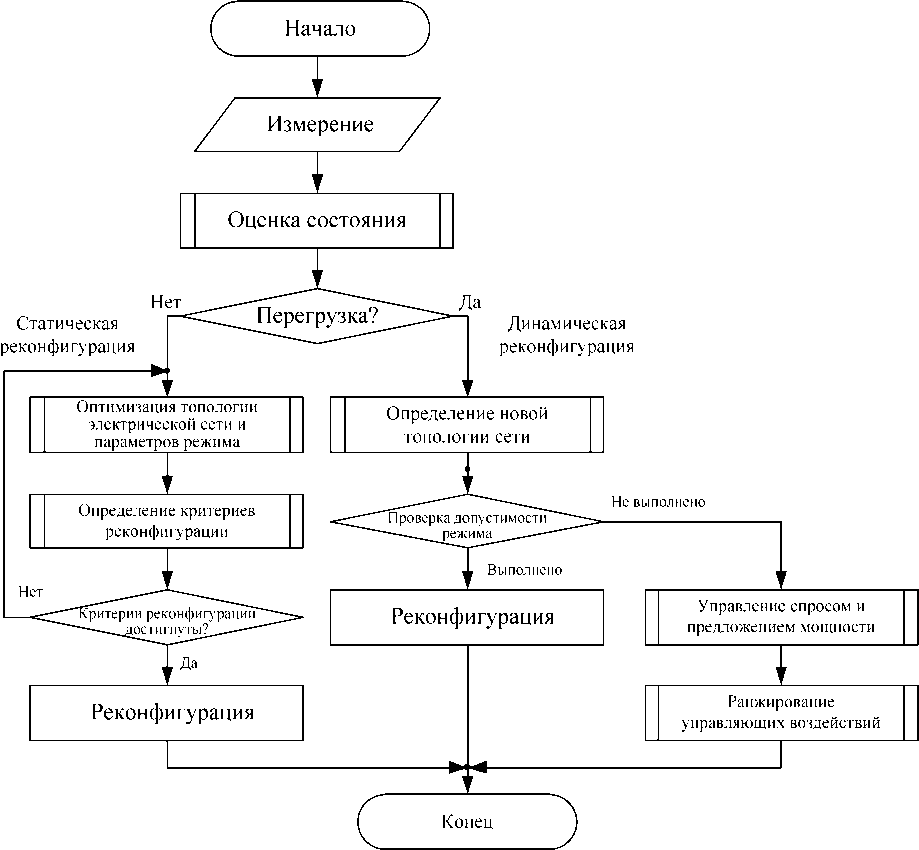
Рис. 3. Алгоритм реконфигурации электрической сети

Система управления реконфигурацией обеспечивает непрерывный контроль и оценку состояния сети, а в случае отсутствия перегрузки элементов электрической сети выполняет оптимизацию новой топологии электрической сети и параметров режима с учетом прогнозных значений спроса и предложения мощности (статическая реконфигурация) [15, 16]. Как правило, реконфигурация электрической сети для оптимизации параметров режима и снижения потерь электроэнергии имеет практический смысл с периодичностью до двух раз в сутки и не всегда оправдана с экономической точки зрения, в отличии от реконфигурации для исключения перегрузки электрооборудования и восстановления нормального режима при аварийных возмущениях.

Определение новой топологии электрической сети при динамической реконфигурации осуществляется на основе решения задачи (2) методом ветвей и границ при соблюдении условий допустимости режима (3).

Метод ветвей и границ базируется на следующих процедурах:

– задание исходного множества вариантов перебора;

– выбор наиболее перспективных множеств при разбиении исходного множества;

– ветвление перспективных множеств на подмножества перебора [17].

Для каждой границы определяется нижняя граница целевой функции, а для конечной вершины – точное значение минимизируемой целевой функции.

Принцип ветвления заключается в обязательном участии и неучастии в дереве какой-либо ветви, т. е. исходное множество допустимых решений разбито на два непересекающихся подмножества: векторы с фиксированным значением 1 и 0. При этом для каждого ветвления дерева электрической сети потери мощности вычисляются рекурсивно по представленным в (1) выражениях без расчета нелинейных уравнений установившихся режимов.

При поиске точки потокораздела электрической сети используется подход, основанный на определении знака потоков мощности в ветвях схемы [17] с полным их перебором. При этом возникает необходимость в дополнительных преобразованиях схемы электрической сети для исключения тупиковых ответвлений ветвей.

В соответствии с представленным на рис. 3 алгоритмом, если исключение перегрузки за счет реконфигурации невозможно по условиям допустимости режима (3), то осуществляется управление спросом и предложением мощности в электрической сети вплоть до отключения нагрузки.

В качестве предложения мощности рассматриваются источники реактивной мощности и распределенной генерации (при наличии).

В данном случае под перегрузкой линий понимается превышение не предельной токовой нагрузки для конкретных типов проводов, а предельных значений токов с учетом обеспечения статической устойчивости и минимально необходимого резерва мощности [18].

Наряду с ограничением мощности потребителей в аварийных режимах соответствующей автоматикой (отключением) предлагается подход с более тщательным разделением потребителей с точки зрения возможного ущерба (стоимости) их отключения в реальном времени и их гибкости в управлении спросом.

Основные способы снижения перегрузки линий:

• –    регулирование активной мощности генератора (при наличии);

• –    регулирование фазового угла (при технической возможности);

• –    настройка графика транзита мощности (им-порт/экспорт);

• –    изменение топологии электрической сети;

• –    сброс нагрузки потребителей;

• –    управление спросом активных потребителей.

Сброс нагрузки является последним вариантом, когда перегрузка линий не может быть уменьшена другими методами.

В рамках реализации распределенного агентного управления потоками мощности в электрической сети [19] при перегрузке предлагаются следующие этапы разрешения указанной проблемы:

• –    предупреждение (наличие потенциальных условий для возникновения перегрузки с учетом прогнозных значений, структуры балансов мощности и прочих факторов);

• –    оповещение (превышение установленных динамических пороговых значений);

• –    аварийный режим;

  – исключение перегрузки.

В качестве основного метода управляемого отключения потребителей при перегрузке элементов электрической сети предлагается использовать чувствительность потоков мощности в линиях к изменению нагрузки на шинах и приоритет нагрузки для указания важности нагрузки в какой-то момент времени. Значения чувствительности на шинах нагрузки используются при расчете необходимого сокращения мощности для снижения перегрузки в линиях электрической сети.

Практическая часть

Рассмотрим реализацию представленных подходов к реконфигурации электрической сети 10 кВ (см. рис. 2). Основные параметры линий представлены в табл. 1, 2.

Моделирование рассматриваемой распределительной электрической сети выполнялось на имитационной модели в MATLAB Simulink. На-

Таблица 1

Сопротивления линий

Линия	1`-1	2-3	3-14	4-5	6-7	8-9	9-2`
r , Ом	0,329	0,266	1,119	0,419	0,464	0,354	0,291
x , Ом	0,099	0,080	0,144	0,102	0,113	0,064	0,087
Линия	3`-10	11-12	13-14	15-16	17-18	18-19	18-4`
r , Ом	0,253	0,160	0,160	0,384	0,278	0,222	0,253
x , Ом	0,076	0,039	0,039	0,094	0,084	0,040	0,076

Таблица 2

Параметры линий

Нагрузка 1 2 3 4 5 6 7 8 9 10 P, кВт 1200 930 1270 1100 820 910 830 560 780 860 Q, квар 1100 870 1140 930 620 820 730 420 650 760 Нагрузка 11 12 13 14 15 16 17 18 19 – P, кВт 760 370 1200 1270 560 715 810 1100 390 – Q, квар 650 290 1150 1100 430 550 725 970 300 – Генерация 3 4 5 6 7 8 12 13 14 15 P, кВт – – – – – – – – – – Q, квар 400 400 – – – – – – – 200 грузка задавалась с учетом типовых статических характеристик по напряжению.

Для предварительной оценки снижения уровня потерь на участке электрической сети в результате реконфигурации был исследован участок с центрами питания ЦП 1 и ЦП 2, исключая ветвь 3-14 (см. рис. 2). Результаты имитационного моделирования с определением потребляемых мощностей по центрам питания ЦП 1 и ЦП 2 при различных местах потокораздела ( δ _ij = 0: 1-2, 2-3, 3-4, 4-5, 5-6, 6-7, 7-8, 8-9) представлены на рис. 4, 5.

Как следует из рис. 4 минимальное потребление мощности от ЦП 1 и ЦП 2 достигается при раздельном питании рассматриваемого участка электрической сети с местом потокораздела 4-5 ( δ45 = 0). Очевидно, что перераспределение нагрузки в ка- кой-то момент времени между шинами может привести к изменению оптимального места пото-кораздела.

В соответствии с представленным на рис. 3 алгоритмом для электрической схемы с четырьмя центрами питания в результате решения оптимизационной задачи реконфигурации (2) были получены оптимальные места размыкания линий и количественные оценки параметров режима (табл. 3). Цель реконфигурации – исключение перегрузки линий 1`-1 и 9-2`. Реконфигурация электрической сети для быстрого снятия перегрузки элементов осуществляется на основе агентного подхода [19, 20] методом ветвей и границ с использованием рекуррентных соотношений для определения потерь электроэнергии для всех участков без расчета установившегося режима.

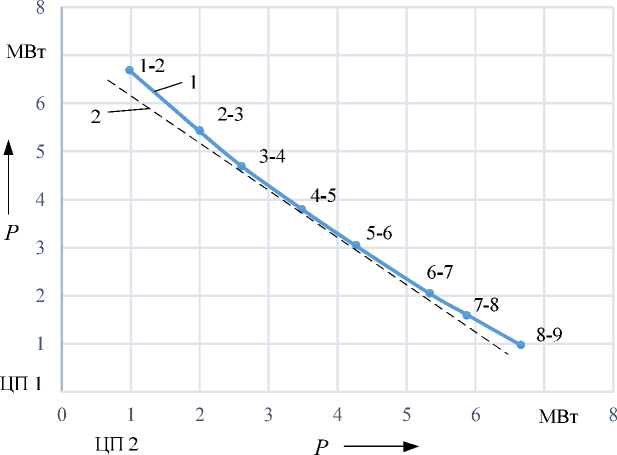
Рис. 4. Потребление мощности центрами питания ЦП 1 и ЦП 2 при разделении электрической сети на два участка с раздельным питанием: 1 – кривая, соединяющая расчетные точки; 2 – касательная к кривой 1 в точке 4-5

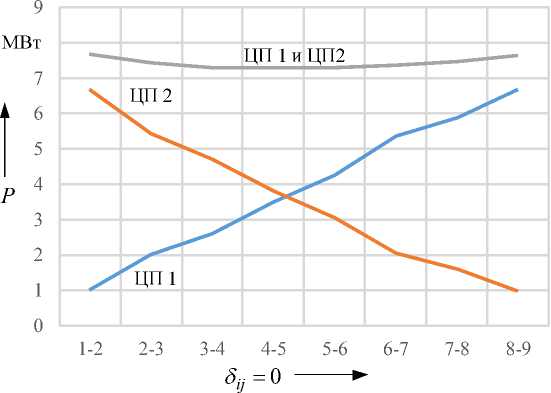
Рис. 5. Потребление мощности центрами питания ЦП 1 и ЦП 2 в различных местах потокораздела

Таблица 3

Режим электрической сети	Потребление мощности
	Тип	ЦП 1	ЦП 2	ЦП 3	ЦП 4	Всего
Исходный	P , МВт	6,225	5,391	2,343	4,134	18,093
δ 34 , δ 1213 , δ 1415 = 0	Q , Мвар	6,12	4,808	2,011	3,527	16,466
После реконфигурации	P , МВт	5,017	4,064	4,688	3,809	17,578
δ 45 , δ 314 , δ 1415 = 0	Q , Мвар	4,447	3,59	4,463	3,344	15,844

Потребление мощности в электрической сети до и после реконфигурации

в

Номер шины ----►

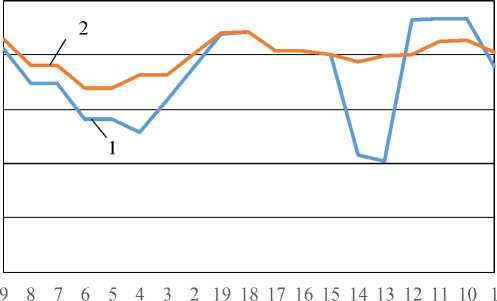
Рис. 6. Напряжения на шинах электрической сети до (линия 1) и после (линия 2) реконфигурации

Номер линии----►

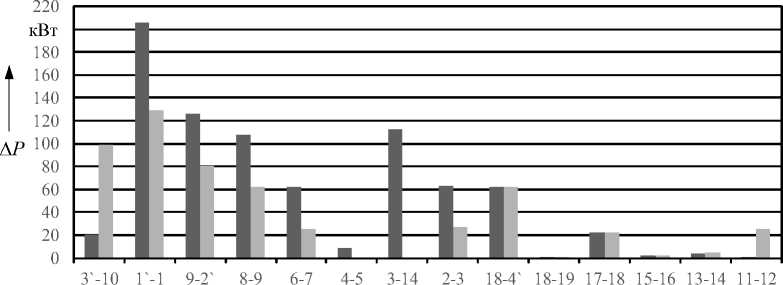
Рис. 7. Потери активной мощности в линиях электрической сети до (левый столбец) и после (правый столбец) реконфигурации

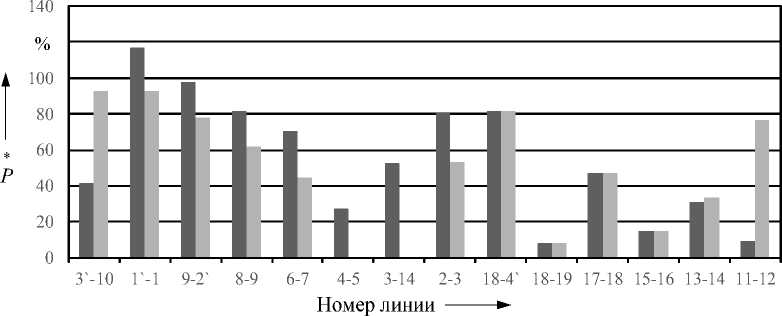
Рис. 8. Загрузка линий электрической сети до (левый столбец) и после (правый столбец) реконфигурации

Из представленных в табл. 3 данных следует, что после реконфигурации потребляемая мощность в электрической сети снизилась на 2,9 %. На рис. 6 представлены результаты имитационного моделирования напряжений на шинах электрической сети, на рис. 7 и 8 – загрузка линий и потери мощности в них.

Общие нагрузочные потери активной мощности в линиях электрической сети составили: 798,08 кВт до реконфигурации и 541,9 кВт после.

Как указывалось ранее, загрузка линий определяется с учетом запаса для обеспечения статической устойчивости (принято 10 %) и минимально необходимого резерва мощности (при необходимости, в том числе по условию n – 1). Таким образом, оптимальная реконфигурация для рассматриваемого случая обеспечила как допустимость режима по напряжению (см. рис. 6), так и исключе-

ние перегрузки линий. Поэтому в данном случае нет необходимости прибегать к ограничению мощности нагрузок и управлению спросом активных потребителей, что является предметом исследований авторов в других работах.

Заключение

Результаты исследований показали обоснованность предложенного подхода к динамической реконфигурации электрической сети для ограничения перегрузки и снижения потерь электроэнергии без расчёта нелинейных уравнений установившихся режимов для каждого варианта изменения топологии сети. При этом в качестве критерия оптимизации топологии электрической сети выступает минимальное потребление электроэнергии при эксплуатационных ограничениях по схемам электроснабжения, допустимым параметрам режима, перегрузкам линий и т. д.