Реконструкция анатомических структур на основе статистической модели формы

В настоящее время в связи с развитием персонализированной медицины задача реконструкции анатомических структур является актуальной. В то время как задача реконструкции органов без деформаций довольно широко описана в литературе, реконструкция в случае деформации органов является нетривиальной задачей, и на данный момент существует несколько подходов к ее решению. Одним из самых популярных методов решения данной задачи является метод статистического моделирования формы [1–7].

Идея метода статистического моделирования формы заключается в предположении, что у каждого органа есть анатомическая форма, имеющая вариативность в некоторых пределах. Под формой в данном методе понимается геометрия объекта в пространстве, инвариантная к определенному классу преобразований. Иными словами, каждая форма является облаком точек, и каждая точка содержит в себе значения координат данной точки в пространстве. Статистической моделью считается средняя форма с некоторой вариативностью. Средняя форма строится в рамках метода главных компонент [8] на основе статистики пациентов, имеющих здоровое анатомическое строение необходимых органов. Таким образом, провести реконструкцию органов с деформацией или частичной утратой можно следующим образом: реконструировать здоровые области, а затем полностью восстановить орган, используя знание о здоровой анатомической форме органа.

В статье приведены результаты исследований по реконструкции формы поражённых лёгких и деформированного черепа. Статистические модели лёгких и черепа строятся по 30 формам обучающего набора соответственно. Пример исходных данных представлен на рис. 1.

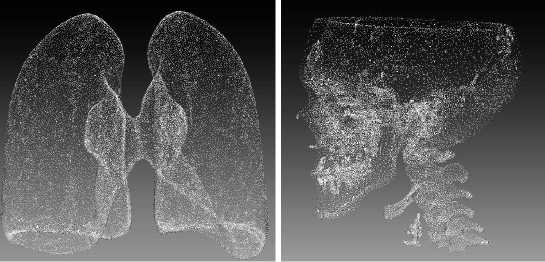
Рис. 1. Пример исходных данных легких (слева) и черепа (справа)

Построение статистической модели формы

В рамках существующих подходов [1, 2, 9] статистическая модель формы представляется как многомерный Гауссов вектор. Каждая компонента вектора

uix

Л

ui = uiy

l uiz )

содержит в себе три пространственные координаты.

Таким образом, в качестве формы S рассматривается облако точек, совокупность пространственных-координат которых удобно представить в форме вектора 3n-мерного пространства, распределенного по

нормальному закону:

S ~ N ( vmean , Σ ),

где

( P 1

\

mean

µ ₂

и

Σ=

l P-12 )

(5„„ u1u1

l    ^u 12 ^u 1

5„„ ) u ₁ u ₁₂

^u 12 ^u 12 /

В свою очередь, каждая компонента вектора vmean и матрицы Σ выражается следующим образом:

	Z ^1 x		'L- . E. . E. . Л ix jx ix jy ix jz
µ i =	^1 y	, 1 uu = ij	E- - E- - E- - iy jx iy jy iy jz	.                (3)
	4. ^1 Z )		E- - E- - E- - ^ izjx izjy iz jz J

области задается скалярное поле ϕ ( u ): ℝ ⁿ → ℝ такое, что ϕ ( u ) является функцией уровней:

ϕ ( u ) =

J d ( u , r ( Q )),u eQ | - d ( u , r ( Q )),u ^Q ,

Элементы матрицы Σ, стоящие на главной диагонали, характеризуют вариативность каждой координаты, а элементы, не стоящие на главной диагонали, описывают взаимную ковариацию двух точек пространства.

Любая форма S выражается как линейная комбинация вектора среднего значения vmean и собственных векторов матрицы ковариации Σ :

^S = vmean + E L ^a - v- , ^a - ^{G N (0} , ^T) .                   ⁽⁴⁾

Схема построения статистической модели представлена на рис. 2.

Формы обучающего набора

I

Совмещение форм

I

Приведение форм в соответствие

Построение статистической модели формы

I

Анализ качества .модели

Рис. 2. Построение статистической модели формы

Все формы обучающего набора имеют произвольные ориентацию и положение в пространстве, поэтому необходимо привести их к одной системе координат.

Совмещение форм проводится в рамках преобразования подобия b :

b ( x ) = k O x + t , x ∈ R ³ ,                              (5)

где k – коэффициент подобия, O – матрица поворота и t – вектор трансляции.

Задача совмещения форм заключается в нахождении такого преобразования b , которое бы решало задачу оптимизации:

b = argmin _{b ∈ B}D_RMS ( b ( S_i ), d ),                       (6)

где n

D rms ( S- , d ) = - E d ²( x ),                         (7)

n l = 1

где x_l – координаты точек формы Si , d ( x_l ) – значение некоторого скалярного потенциала в точке x_l . DRMS ( Si , d ) – среднеквадратическое значение потенциала d ( x_l ) в каждой точке формы Si .

В качестве скалярного потенциала d используется карта расстояний совмещенных форм. Карта расстояний вычисляется следующим образом. На трехмерной где Ω – область внутри формы, Г(Ω): ϕ(Г(Ω))=0 – граница этой области, d(u, Г(Ω)) = infx∈Г(Ω)d(u, x)

В качестве функции d ( u , x ) используется евклидова карта расстояний [10, 11] с учетом знака. Нахождение карты расстояний базируется на понижении размерности и частичном построении диаграмм Вороного. Более подробно алгоритм описан в [12]. Движение в пространстве функции ϕ происходит в направлении нормали в точке u со скоростью v . Таким образом, для функции ϕ выполняется следующее уравнение

∂ϕ / ∂ t = v ∇ ϕ .                                   (9)

Такая функция ϕ неявно задает форму для каждого конкретного случая и является скалярным потенциалом области Ω . Данная функция является функцией уровней и используется в методах функции уровней [13].

Задача оптимизации в (6) и далее решается с использованием алгоритма Бройдена–Флетчера–Гольд-фарба–Шенно с пространственными ограничениями и ограничениями по памяти [14].

Начальная карта расстояний устанавливается как взвешенное произведение всех карт набора с одинаковыми весами. Нахождение средней карты расстояний производится в три этапа. На первом этапе формы совмещаются только с учетом трансляции, на втором – поворота и трансляции, на третьем – масштабирования, поворота и трансляции. После каждого этапа карта расстояний вычисляется как среднее значение всех карт обучающего набора.

Для того чтобы работать с формами как векторами из одного векторного пространства, необходимо привести их к одному виду. После того как все формы обучающего набора совмещены, между формами устанавливается соответствие следующим образом:

f ' = argmin _{f ∈ F}D_RMS ( f ( S_ref ), d ( S_tar )) +γ R ( f ) , (10)

где d ( Star ) – карта расстояний целевой формы, f ( Sref ) – некоторое преобразование над эталонной формой из класса допустимых деформаций, R ( f ) – регуляризующий член, γ – параметр регуляризации.

Класс допустимых преобразований F определяется как Гауссово семейство:

f ( S_ref )~ N ( S_ref , Σ ), f ∈ F .                        (11)

Элементы матрицы ковариации Σ задаются следующим образом:

k ( ui , ul ) = sI 3 exp I - "^ui “l™ I ,                           (12)

I °2 J где I3 – единичная матрица размером 3×3, s – коэффициент масштабирования, σ определяет диапазон расстояний, в пределах которого формы будут корре- лировать. Таким образом, преобразование F будет выглядеть следующим образом:

m f (Sref) = Sref + E aiФi, ai e N(0,1).              (13)

i = 1

Вычисления (11) проводятся итеративно, начиная от больших значений о и заканчивая малыми.

Задача подбора параметров о является задачей оптимизации с несколькими переменными, поэтому подбирать количество итераций и значения о необходимо эвристически на основании некоторых допущений. Предполагается, что на первых итерациях формы не слишком похожи между собой, поэтому коррелировать могут в достаточно больших диапазонах ( о = 50, 60, 70). После каждой следующей итерации формы все больше становятся похожими на среднюю форму, и корреляция ищется в более малых диапазонах ( о = 30, 20, 10, 5). На основе этих предположений подбираются параметры о , близкие к оптимальным в заданных условиях.

Для того чтобы исключить недопустимые деформации модели, при построении статистической модели используется метод главных компонент [8]. Суть данного метода состоит в уменьшении размерности данных (базисных функций) при потере наименьшего количества данных. В рамках метода главных компонент статистическая модель формы определяется как линейная комбинация средней формы vmean и собственных векторов Vi ковариационной матрицы Е ( S) :

M

^S = vmean ⁺ E ^a i vi , ^a i ^{G N (0,} 1),                    ⁽¹⁴⁾

i = 1

где v_mean – средняя форма:

N

Vmean + E Si '                                    (15)

N i = 1

Число компонент M определяет число степеней свободы модели. Каждая новая форма обучающего набора описывается некоторым набором значений a 1 ,^, a m . Таким образом, построенная методом главных компонент модель имеет некоторую вариативность, но при этом форма всегда будет соответствовать анатомической форме органа.

Необходимо отметить, что вариативность модели обусловлена только уникальностью форм обучающего набора. То есть реконструкция формы, не похожей ни на одну из обучающего набора, будет выполнена с высокой погрешностью.

Анализ качества статистической модели формы

Для выбора оптимальной статистической модели (13) с определенным набором параметров о проводится анализ качества каждой построенной модели.

Как правило, для оценки качества статистических моделей формы используются следующие критерии: обобщающая способность модели, компактность и специфичность [15].

Сформулировать критерий оптимальности модели можно следующим образом:

Sopt = { S | о / :min о _i■ G v m^ i Sp v max n ( о , Hmm C } , (16)

где G – обобщающая способность модели, Sp – специфичность, C – компактность модели.

Компактность описывает кумулятивную дисперсию модели. Иными словами, компактность – способность модели описывать вариативность экземпляров формы при заданном количестве компонент.

Компактность можно описать в следующем виде:

M

C ( M ) = E X i ,                               (17)

i = 1

где X i - i -е собственное значение.

Функция C ( M ) определяется как функция от количества компонент модели M .

Обобщающая способность модели характеризует способность модели воспроизводить экземпляры формы, которые не использовались при построении модели. Для оценки обобщающей способности по выборке используется метод скользящего контроля leave-one-out, т.е. по очереди исключается каждый экземпляр формы, строится модель на основе всех оставшихся в обучающем наборе форм и оценивается, насколько точно построенная модель соответствует исключенному экземпляру формы.

Обобщающая способность описывается следующим образом:

N

G =  E DM ( S , S i ),                    (18)

i = 1

где Si – исключенная форма и S ′ i – средняя форма, построенная по оставшейся выборке.

Специфичность модели – способность модели воспроизводить только подобные экземпляры формы. Оценить это качество можно, сгенерировав набор экземпляров формы с помощью модели и сравнив их с экземплярами обучающего набора. Таким образом, специфичность модели можно описать следующим образом:

LN

Sp = 1 EE minijDRMS ( Sj, S ' i ),              (19)

i = i j = 1

где Sj – экземпляр обучающего набора и S ′ i – форма, сгенерированная случайным образом по модели, N – количество форм в обучающем наборе, L – количество сгенерированных форм.

Таким образом, статистическая модель, построенная исходя из критерия (16), является условно оптимальной в заданных условиях. Далее, имея статистическую модель формы органа, можно приступать к реконструкции анатомической структуры.

Реконструкция анатомических структур

Реконструкция в случае частичной утраты или деформации областей органа заключается в восстановлении первоначальной, недеформированной, формы. В идеальном случае реконструированная форма должна повторять контур формы здоровой части органа и дополнять области с деформацией с некоторой приемлемой точностью. Точность реконструированной формы зависит от двух параметров – качества статистической модели формы и точности формы здоровой части анатомической структуры. Процесс реконструкции – совмещение построенной по информации о здоровой области органа формы и статистической модели. Иными словами, реконструкция – получение такого сгенерированного моделью экземпляра формы, который бы максимально соответствовал форме, построенной с использованием информации о форме здоровых областей органа. Данная задача является задачей минимизации среднего расстояния между статистической моделью формы, представленной облаком точек, и изображением функции уровней формы здоровых областей.

Схема процесса реконструкции представлена на рис. 3.

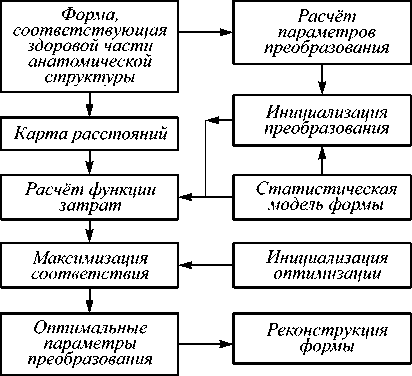
Рис. 3. Схема реконструкции формы органа

Максимизация соответствия между формой здоровой части органа и статистической моделью производится с помощью итеративного метода ближайших точек [16, 17]. Суть данного метода состоит в нахождении минимального расстояния между двумя облаками точек.

В настоящей работе используется модификация метода – нахождение минимального среднеквадратического расстояния между картой расстояний и статистической моделью формы. Нахождение минимального расстояния является задачей оптимизации (10), где в качестве d ( Star ) выступает карта расстояний деформированной формы, а f ( Sref ) является некоторым преобразованием над статистической моделью формы. Таким образом, найдя оптимальные параметры преобразования, максимизирующие соответствие статистической модели и деформированной формы, можно получить реконструированную форму, применив преобразование к Sref :

S' = f '(S ), (20) tar ref где S′tar – реконструированная форма.

В результате процесса (10) получается реконструированная форма, с заданной точностью повторяющая форму здоровой части органа и также с некото- рой точностью дополняющая деформированные или полностью отсутствующие области органа.

Экспериментальные исследования

В настоящей работе исследования по реконструкции анатомических структур проводились на примере легких и черепа. Для построения моделей использовался обучающий набор, состоящий из 30 форм для каждой анатомической структуры. Данные для построения модели были предоставлены Самарским государственным медицинским университетом, а также получены из открытых источников и представляют собой набор изображений легких и черепов, предварительно сегментированных по данным КТ.

Статистическая модель формы состояла из 50 тысяч точек в обоих случаях. Каждая деформированная форма легких состояла из 150–200 тысяч точек, форма черепа содержала около 70 тысяч точек. Итоговая реконструированная форма, как некоторое преобразование от статистической модели, также содержала около 50 тысяч точек.

Легкие

Задача восстановления формы легких актуальна при диагностике интерстициальных поражений, где нельзя однозначно определить область патологии в связи с тем, что в зонах поражения плотность поглощения рентгеновских лучей становится равной плотности мягких тканей, окружающих легкие. Задача автоматической сегментации в данном случае является нетривиальной, ее результат показан на рис. 4 (слева). С помощью статистической модели производится реконструкция формы с деформацией, на выходе получая форму, учитывающую особенности данной формы, но при этом восстанавливающую деформированные области (на рис. 4 справа).

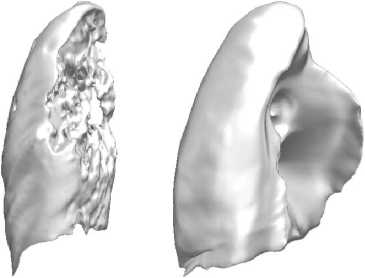
Рис. 4. Реконструкция анатомической формы (справа) по форме с деформацией (слева) на примере левого легкого

Тестовая выборка состояла из 10 форм с деформациями. Для проверки качества алгоритма реконструкции использовались эталонные формы, где врачи-эксперты вручную отметили область, где должны быть легкие. Метрики соответствия восстановленной формы и эталонной представлены в табл. 1 и включают в себя среднее, среднеквадратическое 0,95 – квантиль и максимальное расстояние между формами. Метрики представлены в мм.

Табл. 1. Метрики соответствия эталонных и реконструированных форм

	D mean	Drmse	D 0,95	D max
min	1,661	2,067	3,251	6,212
mean	2,57	3,397	5,17	12,869
max	3,872	5,59	9,732	27,202

Челюстно-лицевой отдел

Задача моделирования челюстно-лицевого отдела также актуальна при планировании хирургического вмешательства. Вследствие некоторых сильных механических повреждений или врожденных патологий в этом отделе могут присутствовать существенные деформации (рис. 4 слева). До оперативного вмешательства необходимо смоделировать челюстно-лицевой отдел без патологии, другими словами, смоделировать планируемый результат операции. Здесь также может быть полезен подход статистического моделирования, так как на некоторой статистике пациентов можно вывести статистическую модель и затем смоделировать расположение черепа для конкретного пациента, учитывая его особенности строения и расположения. Пример смоделированной формы представлен на рис. 5. Слева изначальная форма черепа пациента, справа

– смоделированная.

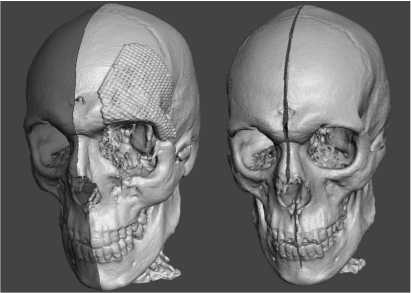
Рис. 5. Моделирование расположения челюсти пациента для последующего хирургического вмешательства

Данная реконструированная форма может использоваться для планирования и прогнозирования результатов операционного вмешательства, а также оценки рисков, связанных с особенностями конкретной формы черепа пациента. В табл. 2 представлены метрики соответствия части черепа без деформации изначального и реконструированного изображений.

Табл. 2. Метрики соответствия здоровой части черепа начальной и реконструированной форм

	D mean	Drmse	D 0,95	D max
min	0,854	1,637	2,443	4,03
mean	1,54	1,798	2,02	9,342
max	3,05	3,98	6,245	17,685

Заключение

В работе показано, что метод статистического моделирования формы является перспективным для задач реконструкции форм с деформациями различных объектов, имеющих некоторую стандартную форму и небольшую вариативность формы. Точность реконструкции зависит от полноты статистической модели и точности алгоритма совмещения форм. Таким образом, метод работает с приемлемой точностью на формах, похожих на формы из обучающего набора, а уникальные формы восстанавливаются хуже, так как они не учтены в статистической модели. Также необходимо отметить, что вариативность формы оказывает большое влияние на точность восстановления формы. Эксперимент с восстановлением формы легких прошел не так точно, как восстановление в случае с черепом за счет того, что форма черепа имеет меньшую вариативность. Точность совмещения также на данный момент является не очень высокой вследствие использования неустойчивого итеративного алгоритма ближайших точек. Качество совмещения форм можно улучшить, применив алгоритм Гауссовой модели смеси, описанный в [18]. Также повышение точности можно получить, используя определенные статические точки (метки), позволяющие однозначно определить ориентиры анатомической формы и проводить реконструкцию с учетом данных ориентиров.

Работа выполнена при поддержке гранта Президента Российской Федерации МД-2531.2017.9 и грантов РФФИ 16-47-630721 р_а, 16-29-09528 офи_м, 17-29-03112 офи_м и Министерства образования и науки РФ.