Реконструкция дефектов в упругих телах сочетанием генетического алгоритма и метода конечных элементов

Введение. Неразрушающий метод контроля (НРК) — контроль свойств и характеристик объекта, при котором не должна быть нарушена пригодность объекта к использованию и эксплуатации. Способ НРК прочности заключается в том, что исследуемая конструкция или материал не подвергается механическим разрушениям, контроль осуществляется косвенно путем измерения и математического анализа физико-механических величин, отвечающих за

Механика

прочностные свойства конструкции или материала.

Существующие методы неразрушающего контроля, такие как радиоволновой, оптический, капиллярный, тепловой, а также радиационный хорошо зарекомендовали себя и успешно используются в производстве и не только. Но с развитием техники и планомерным увеличением удельной производительности ЭВМ возникают новые возможности для проведения неразрушающего контроля. Одним из таких способов является использование эволюционных алгоритмов при распознавании измеряемой акустической информации об инспектируемом объекте. Среди этих методов наибольшее распространение в задачах дефектоскопии получили применение искусственных нейронных сетей (ИНС) и генетических алгоритмов (ГА) на этапе минимизации функционалов невязки между измеренной и рассчитанной информацией. Так применению ИНС при идентификации трещиноподобных дефектов в различных конструкциях посвящены работы [1-4] и др. Разработку и использование ГА в задачах идентификации механических свойств упругих тел и реконструкции дефектов можно найти в работах [5-8], в которых в качестве измеренной информации используются данные о вибрации тел или их резонансных частотах.

В настоящей работе показана работоспособность сочетания метода конечных элементов и генетического алгоритма для решения задач НРК, на примере определения параметров внутренней круговой полости и прямолинейной трещины выходящей на поверхность упругого прямоугольника. Идентификация дефектов основана на минимизации функционалов невязки между данными о наборе первых четырех его резонансных частот.

Постановка обратной задачи. Рассмотрим установившиеся колебания с круговой частотой ю упругого тела, занимающего конечную односвязную область V с границей S . Граница области может быть описана объединением непересекающихся областей S = S 1 U S 2 U S₃, причем на S 1 заданы кинематические, а на S ₂ — силовые граничные условия. Множество S ₃ — это неизвестные границы дефекта (трещина, выходящая на поверхность, внутренняя полость), свободные от напряжений.

Амплитудные характеристики этих колебаний удовлетворяют системе дифференциальных уравнений линейной теории упругости [9]:

с у,j = Рю2ui, ^у = cijkiuk, 1 i = 1,2,3, X e V, (1) и граничным условиям прямой краевой задачи ui Is, = u^, ti Is2 = ^ymj Is2 = Pi, ti Is0 = 0, (2) где ui, ti — компоненты векторов смещений и напряжений; cjkl — компоненты тензора упругих постоянных; р — плотность.

В обратной задаче внутренние границы области S ₃ являются неизвестными, информацией для их определения является набор собственных частот колебаний:

Q = { ю 1 , ю ₂ ,..., ю n }. (3)

На практике наиболее точно определяются набор первых частот, вместе с этим информативность этих данных существенно зависит от вида и размера дефекта, что может быть выражено зависимостью ю_i = ю _i ( S ₃ ), i = 1,2,..., n . Определение внутренней границы S ₃ сводится к нахождению абсолютного (нулевого) максимума функционала, задающего умноженную на -1 норму (в некотором пространстве L ) разности между измеренными резонансными (3) и найденными из решения краевой задачи (1)-(2) собственными частотами ю i = ю i ( S ₃ ), i = 1,2,..., n , где S ₃— заданная конфигурация дефекта, при этом W — область изменения искомых параметров, характеризующих дефект S ₃ , определяется их физическим смыслом. В настоящей работе в качестве такого функционала используется выражение «взвешенной» нормы разности, при которой влияние на его значение изменения всех используемых частот в определенной степени одинаково:

~

F ( $ ₃ ) = -

n s i = 1

1 -

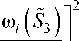
®i( 53 )

~

5 з e W ,

при этом область W изменения параметров, характеризующих область S ₃ , известна и определяется размерами исследуемого образца.

Описание программного обеспечения. Для решения обратных геометрических задач идентификации дефектов разработан и программно реализован комплекс Genetic Algorithm with Finite Element Method in NonDestructive Testing (GAFEMNDT). Данный программный продукт является связующим звеном между модулем ГА «AI::Genetic::Pro» разработанного Strzelecki Lukasz [10] и конечно-элементном пакетом, причем в настоящей работе был использован FlexPDE. Результатом работы GAFEMNDT является набор параметров, обеспечивающий экстремум функции многих переменных.

Система написана на скриптовом языке программирования PERL [11]. Выбор в пользу скриптового языка был продиктован необходимостью оперативно менять целевую функцию, что является не тривиальной задачей для классических языков, таких как Delphi, C++ и т. д. GAFEMNDT представляет собой модульный PERL-скрипт. Целевая платформа для запуска приложения: Linux.

Входными данными для GAFEMNDT является файл, содержащий в себе описание целевого функционала и предельные значения варьируемых переменных.

Выходными данными модуля GAFEMNDT является текстовый файл, содержащий в себе таблицу с результатами расчета. Решением является строка с максимальным значением целевой функции. Простота представления выходных данных позволяет производить визуальный и статистический анализ практически в любом программном продукте, ориентированном на обработку табличных данных, начиная от офисных пакетов Microsoft Office и LibreOffice и заканчивая узкопрофильными пакетами обработки данных, таких как ParaView и VisIt.

Примеры решения задач неразрушающего контроля.

Ниже приведены результаты численных экспериментов по идентификации круговой полости и прямолинейной трещины, выходящей на поверхность прямоугольника под прямым углом. Идентификации подлежат дискретные параметры, характеризующие координаты центра и радиус окружности, или абсцисса точки выхода трещины на поверхность и ее длина. В качестве значений, характеризующих точность идентификации искомых параметров, рассматривались относительные ошибки e , которые вычислялись по формуле:

A - B e = A ’

где A — целевое значение искомого параметра; B — варьируемое расчетное значение этого параметра.

Первым шагом минимизации функционала (4) с помощью ГА является настройка его параметров.

Проведенные численные эксперименты показали, что наиболее рациональными в смысле «точность — время»

являются следующие параметры генетического алгоритма:

Параметры генетического алгоритма

Таблица 1

Параметр	Значение
Размер популяции	128
Разрядность генома	16 бит
Число поколений	<300
Вероятность кроссовера	0,95
Вероятность мутации	0,02
Число родителей	2
Выборка	Рулетка
Стратегия кроссовера	Точечная. 2 точки.
Использовать стратегию элитизма	Да

Механика

Идентификация полости в прямоугольном теле. Описанную методику проиллюстрируем на задачах идентификации внутренних полостей в прямоугольнике, совершающим собственные колебания в рамках задачи плоской деформации. Размеры прямоугольника: длина 0,02 м, ширина 0,01 м, материал — сталь, модуль Юнга E = 20 х 10¹⁰ Н / м ², коэффициент Пуассона v = 0,29 . Правая сторона прямоугольника жестко закреплена, граница внутренней полости свободна от напряжений; X и Y — координаты центра; R — радиус окружности.

Решение обратной задачи идентификации кругового отверстия осуществляется на основе минимизации функционала (4). В качестве инструмента решения прямой задачи использовался метод конечных элементов (МКЭ), реализованный в пакете FlexPDE. Роль «измеренных» резонансных частот выполняет набор первых четырех собственных частот, рассчитанных при заданных параметрах дефекта.

В табл. 2 приведены результаты расчета с помощью GAFEMNDT для 10 примеров прямоугольников с отверстиями, которые были выбраны случайным образом.

Таблица 2

Поиск внутренней полости

№ п/п	Изображение	Параметр	Расчет	Цель	Ошибка, %
1		X	0,003739	0,003739	0,0012
		Y	0,002288	0,002288	0,0121
		R	0,001382	0,001382	0,0032
2		X	0,016465	0,016509	0,2678
		Y	0,001982	0,002027	2,1820
		R	0,000288	0,000287	0,1022
3		X	0,017356	0,017356	0,0005
		Y	0,000921	0,000921	0,0079
		R	0,000623	0,000623	0,0007
4		X	0,010452	0,010452	0,0006
		Y	0,001003	0,001003	0,0032
		R	0,001422	0,001422	0,0005
5		X	0,005504	0,005489	0,2733
		Y	0,000987	0,000999	1,2534
		R	0,000377	0,000376	0,4529
6		X	0,000994	0,000994	0,0017
		Y	0,014685	0,014685	0,0016
		R	-0,000559	-0,000559	0,0324
7		X	0,000675	0,000674	0,1095
		Y	0,010039	0,010043	0,0438
		R	0,000754	0,000751	0,3671
8		X	0,000263	0,000263	0,0043
		Y	0,004963	0,004963	0,0011
		R	0,002378	0,002378	0,0031
9		X	0,000146	0,000146	0,0050
		Y	0,016345	0,016345	0,0001
		R	-0,001924	-0,001924	0,0046
10		X	0,001662	0,001662	0,0011
		Y	0,011621	0,011621	0,0008
		R	-0,000262	-0,000262	0,0410

1 10 19 28 37 46 55 64 73 82 91 100109118 127136145 154163172 181190199208217226235244253 262271280 289298

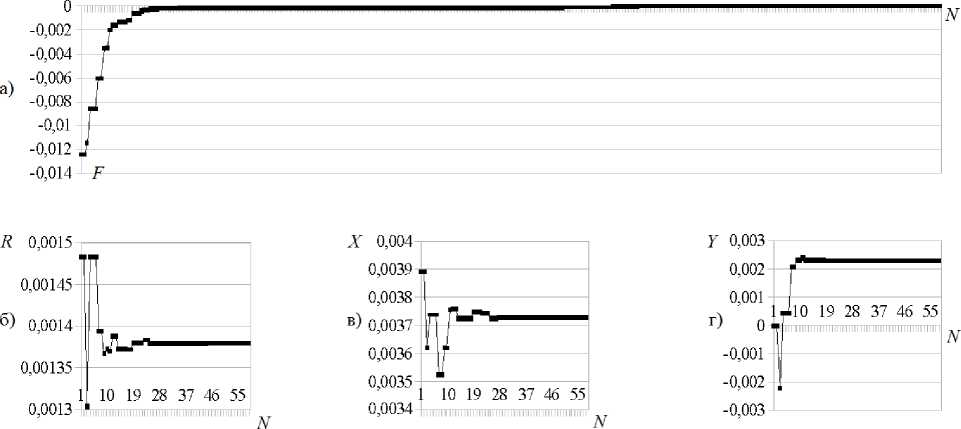
Рис.1. а) Целевая функция; б) R — радиус окружности; в) и г) X и Y — координаты центра окружности

На рис. 1, а представлены графики изменения целевого функционала F (4) и параметров R , X и Y . На рис. 1, б, в и г проиллюстрированы зависимости от N числа эпох ГА для задачи 1 из таблицы 2. Анализ этих результатов показывает, что приемлемая точность идентификации достигается уже при 40 эпохах.

Прямоугольное тело с трещиной, выходящей на поверхность . Вторым примером применения описанной выше методики является идентификация выходящей под прямым углом на поверхность прямолинейной трещины в прямоугольнике длиной 0,05 м, шириной 0,01 м, из того же, что и в п. 3.1, материала. Половина правой стороны прямоугольника закреплена, X0 — координата, где трещина выходит на поверхность, Y1 — глубина трещины (рис. 2).

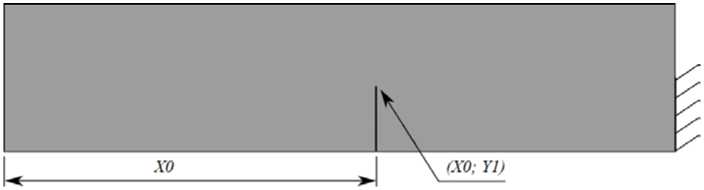
Рис. 2. Модель тела с трещиной

В качестве входных данных были использованы первые три собственные частоты колебаний контролируемого объекта. В табл. 3 представлены результаты идентификации 10 примеров трещин, выходящих на нижнюю сторону прямоугольника.

Таблица 3

Поиск трещины, выходящей на поверхность

№ п/п	Параметр	Расчет	Цель	Ошибка, %
1	X0	0,027813	0,027726	0,313126
	Y1	0,004534	0,004511	0,510042
2	X0	0,021536	0,020737	3,851143
	Y1	0,002861	0,002909	1,665110
3	X0	0,004740	0,004981	4,855177
	Y1	0,002855	0,002702	5,334544
4	X0	0,004938	0,004938	0,002417
	Y1	0,005032	0,005032	0,001143
5	X0	0,042694	0,042701	0,014959
	Y1	0,001943	0,001942	0,062128
6	X0	0,012682	0,012615	0,531135

Механика

	Y1	0,004883	0,004903	0,399785
7	X0	0,019912	0,019915	0,011219
	Y1	0,001901	0,001901	0,012122
8	X0	0,024881	0,024931	0,201769
	Y1	0,001259	0,001261	0,179161
9	X0	0,024716	0,024804	0,354866
	Y1	0,001853	0,001871	0,969296
10	X0	0,009450	0,009402	0,511221
	Y1	0,008899	0,008903	0,048833

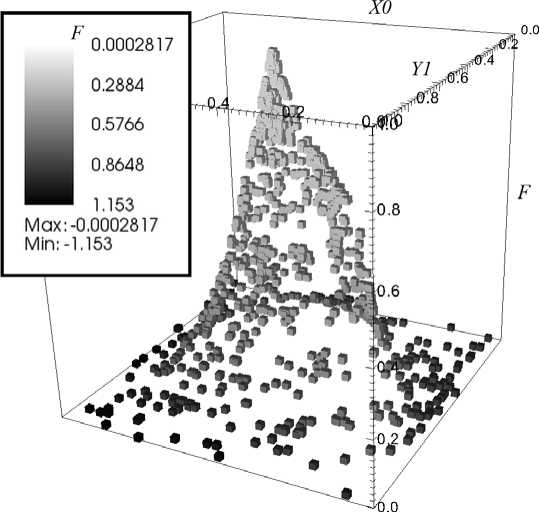
Рис. 3. Целевая поверхность

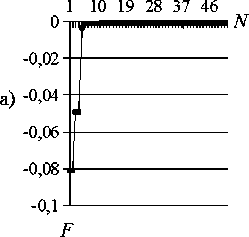
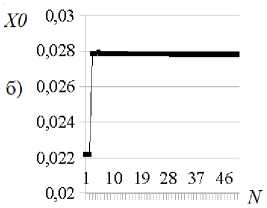
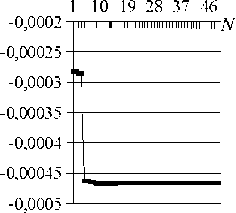
Y1

Рис. 4. а) Целевая функция; б) X0 — координата, где трещина выходит на поверхность;

• в ) Y1 — глубина трещины

На рис. 3 представлен пример целевой поверхности функционала (4) (значения X0, Y1, F нормированы и изменяются в пределах [0;1]). На рис. 4 проиллюстрировано поведение целевой функции и параметров в зависимости от числа эпох N для 1-ой задачи из таблицы 3. Быстрая сходимость алгоритма (20 эпох) обясняется структурой целевой поверхности.

Выводы. Результаты исследования состоят в следующем:

• •    Определены рациональные параметры настройки ГА, представленные в табл. 1.

• •    Для определения трех параметров полости (п. 3.1) с достаточной степенью точности требуется не менее четырех собственных частот колебаний. При этом удовлетворительная точность идентификации достигается при 40

поколениях ГА.

• •    В задаче идентификации трещины (п. 3.2) достаточной информацией оказался набор первых трех резонансных частот, при этом целевая поверхность имеет один экстремум, для нахождения которого достаточно 20 поколений ГА.