Реконструкция МР-изображений с учетом неоднородностей полей

В настоящее время существует несколько методов реконструкции МР-изображений. Реконструкция МР-изображения — это определение распределения плотности протонов (или спиновой плотности) по сечению с ( x , y ) или по объему с ( x , y , z ) на основе измеренного эхо-сигнала S ( t ) [1–5]. Одним из наиболее эффективных является метод Кумара—Велти—Эрнста [2–5], в котором плотность с определяется посредством двумерного или трехмерного преобразования Фурье над эхо-сигналом S ( t ) . Для реализации этого метода существует несколько практических схем [4, 5]. Однако в этом случае требуется высокая степень однородности основного магнитного поля (относительная неоднородность ~10 ^{- 6} ^ 10 ^- 7 ) [6] и градиентных полей ( ~10 3 ) [7], что приводит к большому количеству технических проблем.

Между тем в работах [8–10] предложен метод, математически учитывающий неоднородности полей и позволяющий решать задачу реконструкции МР-изображений в условиях значительной неоднородности магнитных полей ( ~10 1 ).

В данной статье проводится дальнейшее развитие метода, предложенного в работах [8–10] (см. также [5, с. 53–55]).

ЭКСПЕРИМЕНТ В СЛУЧАЕ ОДНОРОДНОСТИ ПОЛЕЙ И ЕГО МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ

Рассмотрим так называемую 1-ю практическую схему эксперимента [4, с. 272], [5, с. 48–49] (см. рисунок). Согласно этой схеме, вдоль z включается градиентное поле Gz = gzz . Вдоль x включается одно градиентное поле Gx = gxx (в прин- ципе бесконечной длительности), т. е. создается частотное кодирование, поскольку этому соответствует постоянство лишь частоты у gxx, где у — гиромагнитное отношение. Вдоль y включается поочередно несколько градиентных полей Gy = gyy с различными gy продолжительностью Ty , т.е. при каждом значении gy создается фазовое кодирование, поскольку каждому эхо-сигналу соответствует постоянство фазы Y gyyTy • При этом для селекции полагается, как обычно, что gz >> gx и gz >> gy [5, с. 46]. Помимо трех градиентных полей включается также статическое поляризующее однородное магнитное поле B0 = const.

Для получения эхо-сигнала от ансамбля протонов (или сигнала спада свободной индукции (ССИ)) создаются π /2- и π -импульсы Карра—Пар-селла (согласно методу эха Ганна). При этом, чтобы устранить расфазирование магнитных моментов протонов (спинов) вдоль z -координаты в пределах эффективной толщины слоя, используется методика Хоулта — изменение направления градиентного поля G_z на противоположное [5, с. 48].

Данный эксперимент требует идеальной однородности полей. Под этим будем подразумевать не только однородность основного поля (B 0 = = const), но и изменение градиентных полей по точным   законам:    G. = g,z, Gx = gxx, zz  xx

G y = g y y .

В условиях такого эксперимента от z -слоя протонов будет исходить ряд эхо-сигналов S (столько сигналов в виде временных процессов S ( t ) , сколько задано значений g_y ). Двумерный эхо-сигнал, идущий от всего z -слоя, с учетом его волновой

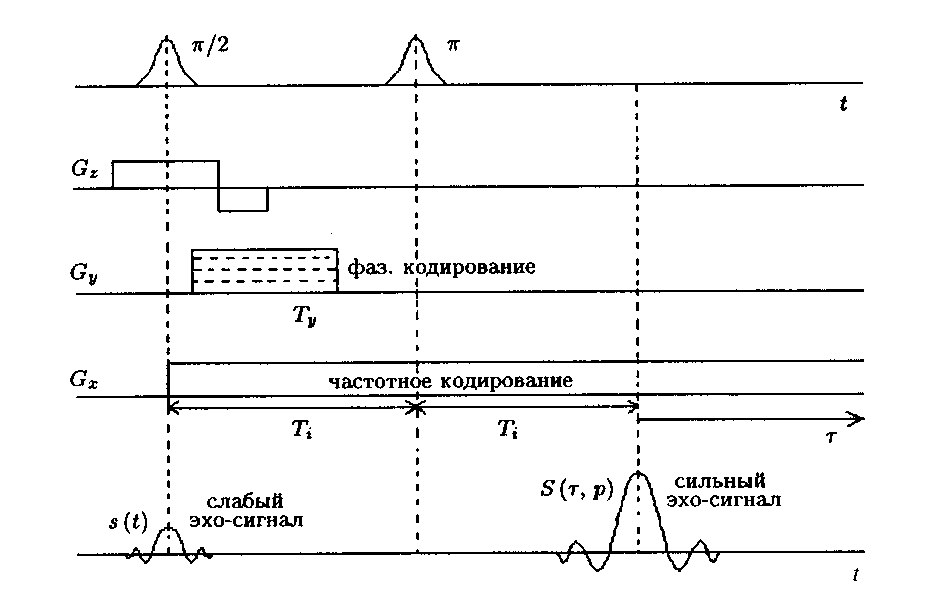
Практическая схема эксперимента

природы можно записать в виде (ср. [5, с. 49])

га то

5 ⁽ t , g y ) = A J J c ⁽ x , У ) ^X

Используя одно из свойств преобразования Фурье — масштабирование (scaling) [4, с. 24], получим:

—ra —TO xexp[ iY(gxxt + B0 t + gyYTy)] dxdy,      (1)

где 5 ( t , g_y ) = S _m ( t , g y ) — измеренный сильный эхо-сигнал, c ( x , y ) = c z ( x , y ) — искомая плотность в z -слое, A — некоторая константа. Запишем (1) иначе:

c

V

^ — to

Y g

y

n

A

^

^

Y T y

x ex

= F

J J ^{5 (} t , g y ) ^x

—

- ^

—

- ^

-p^{[— 1 (} ^ t ⁺ n g y ^{) ] d} t ^d g

y ^,

ra TO

^{5 (} t , g y ) = A J J c ( ^x , У ) ^x

—ra —TO xexP{i [Y(Bо + gxx) t + Y Tyygy)]} dx dУ■     (2)

Введя новые переменные ^ = y ( B 0 + g x x ), П = Y T y y , получим (2) в виде двумерного преобразования Фурье:

^

^

S ( t , g y

) = D JJ

<

c

^ — to

n

x

—

- ^

—

- ^

Y g

y

v.

x exp [ i ( ^ t + n g

y

’ Y T _y

) ] d ^ d n ,

где D = A / ( y ² T y g x ), to o = Y B о .

где F = 1 / (4 ^ ² D ).

Формула (4) позволяет в принципе получить распределение плотности c = c _z по измеренному эхо-сигналу 5 = 5 _to . При этом двумерное непрерывное преобразование Фурье (НПФ) (4) должно реализовываться через дискретное преобразование Фурье (ДПФ) или быстрое преобразование Фурье (БПФ). В этом случае задание равномерных сеток узлов по t , g y , ^ и П породит также равномерные сетки по x = ( ^ — to о ) /( Y g x ) и y = П /( Y T y ) для плотности c .

Для повышения устойчивости вычисления преобразования Фурье предлагается использовать метод регуляризации Тихонова [11]. В этом случае формула (4) запишется в виде регуляризированно-го решения:

' ^to

Y g y

\        to to                  \

, JL = _F f f    S ⁽ t ’ g y ) _x

YT_y      J Ji + aM ( t , g_y )

y J —to —to                 У x eXP[— i (it + Bgy )] dt dgy ’

где a > 0 — параметр регуляризации, a M ( t , g y ) — функция вида

M ⁽ t ’ g y ) =

^ t max

2 n

/

+

g _y

2 n

( g y max J

причем n = i, 2, 3, ... — порядок регуляризации

(обычно n = 1), t_max и g„_m„ — максимальные max        y max

значения t и g _y .

Существует ряд способов выбора параметра регуляризации a [5]: способ невязки (использует значение среднеквадратической погрешности измерения S ), способ подбора и др.

Решение ряда примеров показывает [5, с. 170– 172], [11], что использование метода регуляризации Тихонова уменьшает погрешность вычисления c _a согласно (5) по сравнению с вычислением c согласно (4) (а значит, увеличивает отношение сигнал/помеха) в 2–3 раза.

ЭКСПЕРИМЕНТ В СЛУЧАЕ НЕОДНОРОДНОСТИ ПОЛЕЙ И ЕГО МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ

В предыдущем пункте мы описали эксперимент, использующий высокооднородные магнитные поля. Теперь рассмотрим эксперимент, использующий вместо В o = const неоднородное поле B ( x , y ) = B ₀ + A B ( x , y ), а вместо градиентных полей G _x = g x x и G _y = g _y y — градиентные поля вида G x +A G x ( x , y ) и G _y +A G _y ( x , y ). Здесь A B ( x , y ), A G x ( x , y ) и A G _y ( x , y ) — неоднородности полей. Схема такого эксперимента аналогична схеме эксперимента с однородными полями (см. рисунок).

Математически задача описывается следующим двумерным интегральным уравнением [5, с. 54], [8, 9]:

TO TO

А J J с ( x ’ у ) exp { i [ ^ ( x ’ у ) т + P ( x ’ У ) P ] } d x d У = — to— TO

= s ( т , p ),                                            ⁽⁷⁾

где

^ ^{( x} ’ У ) = Y ^{[ b} 0 ^{+ A B ( x} ’ У ) ⁺ g x x ^{+ A} G x ^{( x} ’ У ^{) ]} ’

^{P ( x} ’ У ) = Y ^[ g y o У ^{+ A G} y ^{( x} ’ У ^)] T y ’ т = t — 2 T .

Здесь A B ( x , y ), A G _x ( x , y ), A G _y ( x , y ) — неоднородности полей. Имеются в виду неоднородности, обусловленные в первую очередь техническими особенностями. Под A B подразумевается отклонение от B = B ₀ = const, а под A G _x и A G _y — отклонения от законов g _x x и g _y y . Например, если магнитное поле создано одной катушкой в виде соленоида с однородным распределением тока вдоль ее обмотки, то поле B будет падать от центра катушки к ее краям в = 1.5 раза в типичных случаях [5, с. 59], а от оси катушки к ее обмотке возрастать. Ставится задача: в условиях высокой неоднородности полей выполнить реконструкцию МР-изображения, т. е. найти функцию c ( x , y ) = c z ( x , y ) путем решения уравнения (7).

Отметим свойства функций A B ( x , у ), A G _x ( x , y ), A G _y ( x , y ), которым они должны удовлетворять, чтобы задача реконструкции имела решение и притом единственное. Функции A B ( x , у ), A G _x ( x , y ), A G _y ( x , y ) должны быть известными гладкими детерминированными (неслучайными) функциями x и y . Существующими в настоящее время техническими средствами можно добиться выполнения данных свойств неоднородностей магнитных полей.

Рассмотрим ряд градиентных полей по у , рав^ных P ^[ g y 0 У ^{+ A G} y ^{( x} ’ У )], где P e [ P min ’ P max ] , g y 0 ^ 0, например, g y o = min | g y I ^ 0, а p = = ± i, ± 2, .

Остановимся на способе решения уравнения (7) относительно c ( x , y ). Введем новые переменные

i = ^ ( x , y ), n = P ( x , y ).

Систему нелинейных уравнений (СНУ) (8) относительно х и у запишем подробнее:

Y В 0 + Y ^{A B (} x ’ У ) + Y g x x ⁺ Y ^A G x ^{( x} ’ У ) = ^ ’ Y g y 0 yT y + Y A G y ( x , y ) T y = n .

Запишем систему (9) в виде, удобном для решения методом итераций:

i — to 0   A B ( x , y ) + A G x ( x , y )

Y g x             g x

П     ^A G y ⁽ x ’ y )

Y g y 0 T y       g y 0

где го ₀ = у B ₀. При этом d x d y = | J ( 4 , n ) | d 4 d n , где

	d x	д x
J ( 4 , n ) =	д4 д У	dn д У
	д4	dn

— якобиан преобразования.

В результате решения СНУ (10) некоторым итерационным методом (Ньютона, хорд и т.д.) получим x = x (4 ,n), | y = y(4, n) J где x(4,n) и y(4,n) — некоторые численные зависимости.

Уравнение (7) можно записать в виде двумерного НПФ:

те те

А J J с ( x( 4 , П ), У ( 4 , П ) ) х

-те-те хexp[i (4т + np)] | J(4,n)|d4 dn =

= ^s ( ^т , P ).                                    (11)

Обращение (11) с помощью обратного преобразования Фурье по аналогии с решением уравнения (3) приведет к формуле

Ас ( x ( 4 , n ), У ( 4 , n ) ) | J ( 4 , n )| =

1     тете

= —— I* f s ( т , p )exp [ - i ( 4 т + n p ) ] d T d p , 4 n ² J J

-те-те откуда искомое решение равно с (x (4, n), У (4, n ))= тете

= Q( 4 , n ) J J S ( т , p )exp [ - i ( 4т + n p ) ] d т d p , (₁₂)

-те-те где

Q ^{( 4 ,} n ) = , 2 Ы M ■ 4 n A\J ( 4 , n )|

Для повышения устойчивости решения (12) используем метод регуляризации Тихонова. Решение (12) с регуляризацией будет иметь вид:

с а (x(4 , n), У (4 ,n))= s (т, p)

1 + a M ( т , p )

тете

= Q 4n ) J J

-те-те

х

х exp [ - i ( 4т + n p ) ] d т d p ,             (13)

где (ср. (6))

Г      Л² ”

M ( т , p )

т

^ max

p

^ ^p max

2 n

/

Параметр регуляризации а может быть выбран различными способами, например способом подбора контрастности изображения (чем меньше а , тем выше контраст томограммы, и наоборот) или способом невязки из уравнения [5, с. 55], [11]

тете

JJ |~( т ■ p )[

-те -те а M (т, p) 12

1 + a M ( т , p )

d т d p = 5 ²

при условии тете

J J |S(т,p)| dтdp>52, -те -те где

I ~-s i:, ^ 5 2, т.е. 5 — среднеквадратическая погрешность измерения эхо-сигнала S(т, p), полагаемая известной ( s — точный эхо-сигнал, а s — измеренный эхо-сигнал).

В работе [8] приведены результаты численного решения уравнения (7) (без регуляризации). В модельных примерах полагались следующие неоднородности полей:

А В /В ₀ = 3.6 - 10 ^{- 5} , A G _x/ g _x = 3.4 мм,

A G y/ g y = 4.1 мм или A g x/ g x = 2.8 - 10 ^{- 2} ,

A g y/ g y = 2.8 - 10 ^{- 2}.

Однако данная методика может быть использована и в случае, когда ^А В/В 0 , ^А g x/ g x и ^А g y/ g y имеют заметно большие значения. Необходимо только знать функции A B ( x , y ), A G _x ( x , y ) и A G _y ( x , y ). Они могут быть рассчитаны численно на основе заданной конфигурации катушек и распределения токов в них, например, по методике, изложенной в работах [6, 7]. Кроме того, возможно, что использование метода инвариантных аппроксимаций [12] позволит существенно уменьшить влияние неоднородностей магнитных полей при решении уравнения (7). Однако этот вопрос требует специального рассмотрения.

Применение метода регуляризации Тихонова для повышения устойчивости решения (12), как показывают примеры, рассмотренные в работе [11], понижает отношение | A с _а |/ с _а в 2-3 раза

(где ∆ с _α — погрешность решения с _α ).

При численной реализации метода непрерывное преобразование Фурье (НПФ) (13) заменяется на дискретное преобразование Фурье (ДПФ) или на быстрое преобразование Фурье (БПФ) на равномерных сетках узлов по τ , p , ξ , η . В результате решение c _α будет получено на неравномерных сетках узлов по x , y . Поэтому в дальнейшем необходимо применение интерполяции.