Реконструкция ориентации действующих на "бесконечности" напряжений в пределах Ковдорского рудного узла на основе натурных определений

В течение последних 30 лет Горным институтом КНЦ РАН проводятся исследования, целью которых является изучение возможностей увеличения углов наклона бортов карьеров в массивах прочных скальных пород [1; 2]. Одним из основных объектов, на котором выполняются исследования прибортового скального массива, является карьер рудника "Железный" АО "Ковдорский ГОК", где удалось обосновать возможность формирования высоких вертикальных уступов, при этом величина генерального угла борта карьера составляет от 45 ° до 60 ° в зависимости от инженерно-геологических и геомеханических условий [3; 4]. Полученный результат объясняется учетом параметров напряженного состояния массива пород, которые оказывают влияние на устойчивость бортов и уступов в сторону ее увеличения при соответствующих условиях.

Материалы и методы

Многочисленными измерениями, выполненными методом разгрузки в варианте торцевых измерений, показано, что в прибортовом массиве пород при условии применения щадящих технологий производства взрывных работ действует поле напряжений гравитационно-тектонического типа. К настоящему времени проведено более 25 измерений непосредственно с уступов карьера на специальных наблюдательных станциях с использованием горизонтальных скважин [5; 6].

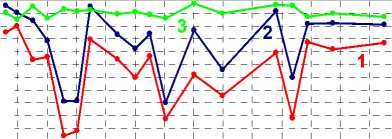
На рис. 1 в качестве примера показана типовая конструкция станции по измерению параметров напряженного состояния породного массива мето Н 2 ф ия напряжений по длине скважины.

-90

0 -10 -20 -30 -40 -50 -60 -70 -80

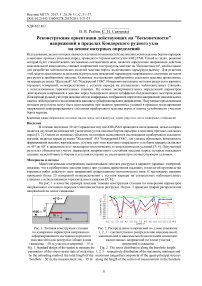
0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0 11,0 12,0 13,0 14,0 Длина, м

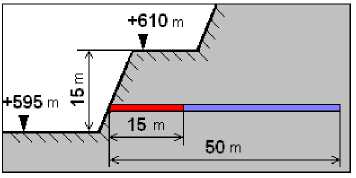
Рис. 1. Типовая конструкция станции по измерению параметров напряженно-деформированного состояния породного массива методом разгрузки: общая длина скважины – 50 м, участок измерений – 15 м Fig. 1. Standard design of the station to measure the parameters of the stress-strain state of rock mass by the unloading method: the total length of the borehole – 50 m, the measurement site – 15 m

ис. . аспределение напряжени по длине скважины:

1, 2, 3 – соответственно распределение максимальной, минимальной и максимальной касательной компонент квазиглавных напряжений по длине участка измерений в скважине

Fig. 2. The stress distribution along the borehole length:

• 1,    2, 3 – respectively distribution of the maximum, minimum and maximum tangential component of the quasi-principal stresses along the length of the section of measurement in the borehole

Результаты и обсуждение

Постановка задачи

В то же время при разработке математических моделей массива пород, включающих карьерную выемку, возникает задача определения направления действия максимальной компоненты главных напряжений в нетронутом массиве на "бесконечности". Для решения этой задачи можно использовать результаты измерений параметров напряженного состояния методом разгрузки в прибортовом массиве.

Решение задачи

Введем следующие предположения:

• а)    полагаем, что на некоторой глубине контур карьера в плане представляет эллипс с полуосями а и b ;

• б)    конформное отображение внешности эллипса на внутренность единичного круга осуществляет функция:

<0 = R I- + -I,                                   (1)

a - b где m =----, g — точка внутри внешности эллиптического отверстия, R — радиус этой точки. При R = 1

a + b и ς = 1 получаем контур заданного эллиптического отверстия.

Тогда при действии на "бесконечности" напряжений о” = - р (рис. 3) имеем тангенциальные напряжения на контуре отверстия [7]:

1 -m ² + 2 m cos2 α- 2cos2( θ-α ) 1 - 2 m cos2 θ+m ²

где θ – угол между осью ОХ и точкой на контуре эллипса, α – угол между осью ОХ и направлением действия

______ ______V СО напряжений о x = -р .

Рис. 3. Схема для определения напряжений при действии сил о ” = - р

Fig. 3. Scheme for determining the stress under the action of forces о ” = - р

При действии на "бесконечности" сил ст ” = - q (рис. 4) имеем тангенциальные напряжения на контуре отверстия:

1 -m ² - 2 m cos2 α+ 2cos2( θ-α ) σ θ = q                             ₂          ,

1-2mcos2θ+m ²

где θ – угол между осью ОХ и точкой на контуре эллипса, α – угол между осью ОХ и направлением действия напряжений и ” = - q .

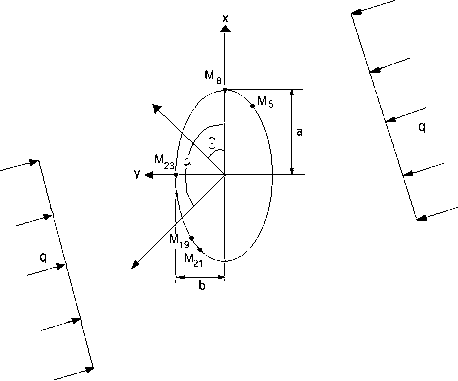
Рис. 4. Схема для определения напряжений при действии сил и ” = - q

Fig. 4. Scheme for determining the stress under the action of forces и ” = - q

При совместном действии сил а ” = - р и и y = - q имеем тангенциальные напряжения на контуре отверстия:

1 -m ² + 2 m cos2 α+ 2cos2( θ-α ) р

1 - 2 m cos2 θ+m ²

₊ 1-m ² -2mcos2α+2cos2(θ-α)

1 - 2m cos 2θ + m ²

Для определения величин p и q из (4) необходимо иметь две точки на контуре эллиптического отверстия, полученные экспериментальным путем. При этом следует решить систему уравнений:

σ _θ

_о ⁽²⁾ σ _θ

1 - m ² + 2m cos 2 а- 2cos2(0! - а )   1 - м ² - 2м cos 2а + 2cos2(0! - а)

= Р -----------------------------9--- ¹----- + Q----------------------------- 9---¹-----

1 - 2m cos 2 0 1 + m ²                    1 - 2м cos 20 1 + м ²

_ 1 - м ² + 2м cos 2а- 2cos2(0 ₂ - а)   1 - м ² - 2м cos 2а + 2cos2(0 ₂ - a)

P       1 - 2м cos20 ₂ + м ²          ^       1 - 2м cos20 ₂ + м ²

В таблице представлены параметры напряженного состояния массива пород, полученные по результатам измерений методом разгрузки, а также напряжения в массиве, рассчитанные на основе действия собственного веса вышележащих пород (в последующих рассуждениях растягивающие напряжения принимаются положительными, сжимающие – отрицательными).

Таблица. Параметры напряженного состояния массива по результатам измерений методом разгрузки Table. Parameters of the massif stressed state according to the results of the discharge method measurements

CD M и Щ Щ о	Станция, горизонт, год измерений, участок борта карьера	g s ю	Параметры напряженного состояния массива пород по результатам измерений		Отношение максимальной компоненты главных (сжимающих) напряжений к расчетным вертикальным напряжениям исходя из действия только собственного веса пород σ max / γ Н
			σ max , МПа	σ min , МПа
М 5	Н/С-5, +40 м, 2005, сев.-вост.	217	–13	–4	2,0
М 8	Н/С-8, +10 м, 2007, северный	247	–20	–3	2,7
М 19	Н/С-19, +40 м, 2011, южный	175	–13	–7	2,6
М 21	Н/С-21, +10 м, 2012, южный	250	–28	–4	3,5
М 23	Н/С-23, +70 м, 2012, юго-зап.	170	–24	–9	4,8

Примечание: γ – собственный вес пород ( γ = 3 т/м ³ ).

В рассматриваемой задаче при последующих рассуждениях в полярных координатах σ θ соответствует σ _max .

Рассмотрим несколько примеров.

По нашим данным имеем a = 5 усл. ед.; b = 3,5 усл. ед., следовательно, m = 0,1765. Из таблицы для точки M 8 получаем α = 0, θ = 0, σ θ = –20 МПа; для точки M 23 соответственно α = 0, θ = 90°, σ θ = –24 МПа. Отсюда на основе (5) получаем систему уравнений:

• - р + 3,858q = - 20,

• 2,4 p - q = - 24.

Решение данной системы уравнений: p = –13,63 МПа, q = –8,72 МПа.

Возьмем теперь точки M 8 и M 21 , для которой α = 0, θ = 150°, σ θ = –28 МПа.

Отсюда система уравнений:

- p + 3,858 q = - 20, 0,377 p + 1,887 q = - 28.

Решение системы уравнений: p = –20,96 МПа, q = –10,63 МПа.

Рассматривая точки M 5 со значениями α = 0, θ = –27°, σ θ = –13 МПа и M 19 с параметрами α = 0, θ = 140°, σ θ = –13 МПа, имеем систему:

0,177 p + 2,177 q =- 13, .1,004 p + 0,994 q = - 13.

Получаем решение в виде: p = –7,66 МПа, q = –5,35 МПа.

Если взять среднее значение отношения p / q по нашим расчетам, то получим p / q = 1,656. По результатам определения напряженного состояния в окрестности карьерной выемки, выполненного с учетом геологического строения Ковдорской интрузии p = –1,05 усл. ед., q = –0,85 усл. ед. [8]. Здесь отношение p / q = 1,235. Иными словами, относительная погрешность к наибольшему значению отношений составляет 25 %. Во всех рассматриваемых случаях мы получили p >  q , т. е. в направлении длинной оси карьера действуют большие напряжения, чем в направлении короткой (рис. 5).

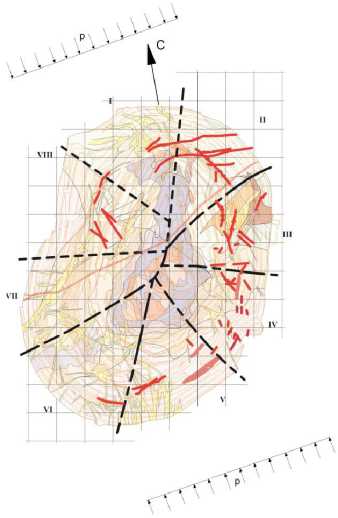
Рис. 5. Ориентация максимальной компоненты главных напряжений на "бесконечности" в нетронутом массиве Ковдорского рудного узла: различными цветами обозначены различные типы руд и вмещающих пород; красными линиями обозначены крупные структурные нарушения в пределах карьера; черными пунктирными линиями – границы инженерно-геологических секторов (обозначены римскими цифрами) Fig. 5. Targeting the maximum component of the principal stress on the "infinity" in the pristine massif Kovdor ore unit: different colors represent different types of ore and host rocks; red lines represent major structural irregularities within the quarry; black dotted lines – the boundaries of engineering and geological sectors (denoted by Roman numerals)

Заключение

На основе выполненного анализа можно сделать вывод, что максимальная компонента главных напряжений в нетронутом массиве Ковдорского рудного узла действует в субмеридиональном направлении (рис. 5). Данный вывод имеет большое значение для оценки уровня действующих напряжений непосредственно в прикарьерной зоне, используется при задании граничных условий в процессе моделирования напряженно-деформированного состояния прибортового массива пород и оценке устойчивости участков борта карьера.

Исследования выполнены в рамках гранта по приоритетному направлению деятельности РНФ "Проведение фундаментальных научных исследований и поисковых научных исследований отдельными научными группами" № 14-17-00751.