Реконструкция ВОЛП с включением компенсирующих волокон в муфтах оптического кабеля

Современные сети связи развиваются в условиях непрерывного роста потребностей в увеличении их пропускной способности, что делает крайне актуальной задачу реконструкции волоконно-оптической линии передачи (ВОЛП) для работы на более высоких скоростях. В настоящее время для региональных сетей связи актуален переход к скоростям передачи 10 Гбит/с и выше. Для этой цели перспективным может быть применение солитонов, управляемых за счет изменения дисперсии вдоль линии передачи [1-2]. В частности, так называемого режима управления дисперсией на плотных схемах компенсации – DDMS (Dense Dispersion Management Soliton) [4-6].

Для реализации такого режима требуется компенсация хроматической дисперсии, которая осуществляется включением оптических волокон (ОВ) с дисперсией противоположного знака. При реконструкции ВОЛП это может быть заме- на строительных длин оптического кабеля (ОК). Однако при разработке проектов реконструкции ВОЛП, необходимо учитывать стоимость отвода земли под строительство и, соответственно, стоимость инфраструктуры в целом. Уже сегодня затраты на землеотводы и согласования составляют большую часть затрат на строительство ВОЛП. По прогнозам в перспективе эта тенденция будет только усугубляться [3]. Как следствие, одним из требований к проектам реконструкции ВОЛП является минимизация объемов работ на линейнокабельных сооружениях в целом и, по возможности, исключение работ по прокладке и замене ОК. Этим требованиям отвечает вариант реализации DDMS с включением компенсирующих дисперсию ОВ (DCF – dispersion compensation fiber) в муфты ОК.

Исследованию возможности работы ВОЛП в режиме DDMS при включении компенсирующих ОВ в муфтах ОК и посвящена данная работа.

Распространение управляемого дисперсией солитона в оптической линии

Реализация DDMS предусматривает чередование с заданным периодом ОВ строительных длин кабеля с положительной и отрицательной хрома- тической дисперсией в соответствии со схемой компенсации, которая также называется дисперсионной картой (ДК). Для данного варианта организации режима управления дисперсией период компенсации дисперсии, то есть период ДК, много меньше расстояния между оптическими усилителями (ОУ). И в простейшем случае ДК представляет собой оптическую линию из двух последовательно соединенных разнотипных ОВ.

Как известно, распространение оптического сигнала в линии с управлением дисперсией описывается модифицированным нелинейным уравнением Шредингера (МНУШ) с переменными коэффициентами. Для комплексной огибающей амплитуды электромагнитного поля МНУШ имеет вид [2, 4-9]:

.QA-P^Q ^+ ^2).|л|2.л = 0, (1)

8Z 2 5/^{2 Z 7}

Здесь Z – нормированное расстояние вдоль оптической линии; t – время; – периодическая функция,описывающая изменение параметра дисперсии групповых скоростей (ДГС); – коэффициент керровской нелинейности, зависящий от Z ; – периодическая функция, описывающая изменение пиковой мощности квазисолитонного импульса между двумя усилителями. Уравнение (1) описывает усредненные модели и поэтому параметр дисперсии групповых скоростей и коэффициент нелинейности малы.Уравнение(1) учитывает,что при распространении в оптической линии групповой сигнал испытывает воздействия затухания, периодического усиления, действие фазовой самомо-дуляции и дисперсионных эффектов.Учет влияния четырехволнового смешения и поляризационных эффектов при записи (1)не производился.

Известно решение (1) на основе вариационного подхода при использовании лагранжиана вида [2; 4; 6-9]:

Используя вариационный подход к решению (1), можно перейти к решению системы из двух обыкновенных дифференциальных уравнений для длительности T и чирпа C [2; 6]:

^-^'

SC _/Eoc(Z)

8Z ^T

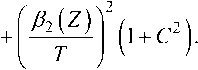
Очевидно, что свойства управляемого дисперсией солитона зависят от параметров ДК. Для случая двухсегментных ДК в [2, 6] приведена зависимость входной длительности импульса от параметров ДК:

T map

\PlnhiPlJa\

Wn-P4ja ‘

Здесь – параметр с размерностью времени, включающий только четыре параметра дисперсионной карты. предоставляет временной масштаб для произвольной дисперсионной схемы такой, что устойчивые периодические решения имеют длительность входного импульса, близкую к – значения параметров ДГС секции с аномальной и нормальной ДГС ОВ длинами и соответственно.

Для передачи информации используются фундаментальные светлые солитоны. Фундаментальному солитону отвечает оптический импульс, параметры которого задаются выражением [2; 6]:

^-Z^L-i

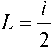
8A /

A--A

8Z

8A

8Z

^-ы^2

и усредненного вариационного принципа в предположении гауссовой огибающей оптического импульса:

A(Z,t) = яехр

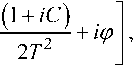
где N определяет порядок солитона, а – мощность входного импульса.

Важное свойство оптических солитонов – это их высокая устойчивость к возмущениям. Поэто-му,хотядлясозданияфундаментальногосолитона и требуется специальный профиль и определенная пиковая мощность при заданных параметрах, отвечающая условию (4), но он может быть сформирован, даже если форма профиля и пиковая мощность отклоняется от идеальных условий. В частности, фундаментальный солитон можно создать при условии [1-2; 6]:

0,5 <  N² <1,5.

где – амплитуда одиночного импульса, T , C , – его длительность, чирп и фаза соответственно.

Модель ВОЛП

На основе решения системы уравнений (2) была создана компьютерная модель кусочно-ре-

гулярной волоконно-оптической линии передачи. Для данной модели в качестве исходных данных при моделировании регенерационного участка (РУ) ВОЛП мы задавали тип и характеристики ОВ, длину РУ, количество и параметры ОУ на РУ, номинальную длину периода компенсации и схему компенсации. Длина усилительного участка определялась из условия равенства расстояний между ОУ на РУ. Номинальные значения длины сегментов рассчитывались по заданной глубине компенсации хроматической дисперсии в зависимости от типа схемы и длины периода компенсации. При моделировании мы ограничились случаем амплитудного формата модуляции АМ. В целях упрощения математической модели мы рассматривали случай идеальной компенсации потерь оптического сигнала в линии. Исследуя искажения оптических импульсов, мы ограничились влиянием только межсимвольной интерференции и не учитывали солитон-солитонного взаимодействия и джиттера. Шум усилителей учитывали по методике, представленной в [10]. Качество передачи оценивали по уширению оптических импульсов на выходе РУ.

При реализации DDMS предложенным нами методом вмешательство в линию ограничивается повторным монтажом муфт или их возможной заменой. Как отмечалось выше, предельная скорость работы ВОЛП на основе DDMS определяется параметрами ДК. И поэтому поддерживаемая входная длительность оптического импульса тем меньше, чем меньше период ДК, средняя остаточная дисперсия в линии и локальные значения дисперсий ОВ. Большинство эксплуатируемых оптических линий связи построены на ОК со стандартными ступенчатыми ОВ по рекомендации МСЭ – Т G.652 (SMF – single–mode optical fiber), но известны ВОЛП, построенные на ОК с ОВ по рекомендации МСЭ – Т G.655 (NZDSF – non–zero dispersion shift optical fiber). Таким образом в соответствии с формулой (3) для осуществления возможности передачи оптического импульса формата RZ (return – to – zero), которая отвечает битовому интервалу для 10 Гб/с, необходима длина сегмента ДК с SMF около 4 км (для условия использования SMF с типичными параметрами и компенсирующего дисперсию ОВ DCF со значением дисперсионного параметра –100 пс2/нм.км).

Следует отметить, что при выборе типа компенсирующего ОВ требуется учитывать вносимое затухание и крутизну характеристики. Увеличение вносимых потерь в линейный тракт может привести к необходимости увеличения количества ОУ или к увеличению коэффициента усиления ОУ. Для использования DCF в муфтах ОК желательно, чтобы ОВ обладало большим значением дисперсии. Это поможет увеличить количество ОВ, компенсация дисперсии на которых необходима, и напрямую связано с габаритными размерами модуля компенсации дисперсии, причем фиксированной длины. Таким образом, при рассмотрении вариантов реализации DDMS для компьютерного моделирования мы использовали двухсегментные ДК, параметры которых представлены в таблице 1.

Таблица 1. Параметры ДК, используемые при моделировании

Тип ДК	#1	#2
Тип ОВ а	NZDSF(+)	SMF
Тип ОВ б	DCF для NZDSF	DCF
1а, км	4	4
, пс2/км	–0, )1	–0,
Скорость	10 Гб/с	10 Гб/с

Результаты моделирования передачи сигналов в режиме DDMS

Поскольку большинство ВОЛП построены на SMF, представляет интерес более подробное рассмотрение ДК #2. В качестве исходной линии для расчета была взята ВОЛП с номинальным усилительным участком длиной 80 км, параметром шум-фактора ОУ в 5дБ и протяженностью в 400 км, что соответствует статистической протяженности линии связи, характерной для региональных сетей. Результаты моделирования для ДК #2 представлены на рис. 1-3.

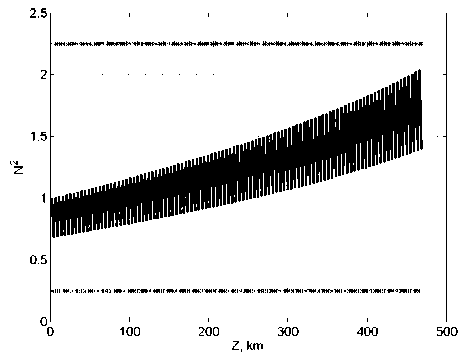
Рис. 1. Зависимость параметра N вдоль линии, отображающая условие существования солитона для #2 ДК

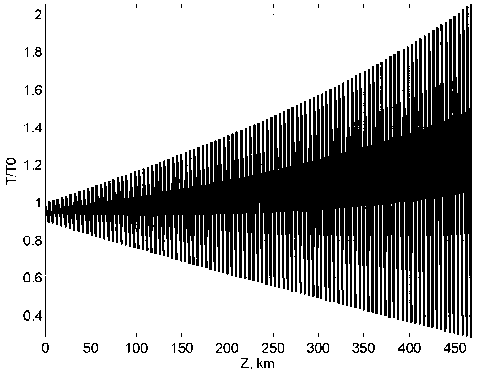
Рис. 2. Нормированная длительность оптического импульса вдоль линии для #2 ДК

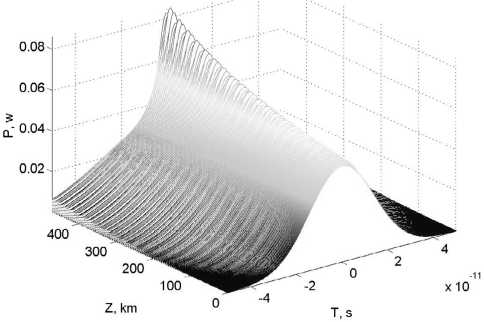
Рис. 3. Динамика распространение солитона вдоль оптической линии для #2 ДК

Результаты для ДК #1 во многом аналогичны представленным расчетам для ДК #2. Полученные данные позволяют говорить о том, что передача оптических импульсов может быть осуществлена с приемлемым качеством даже в случае АМ сигнала.

Таким образом, включение DCF в муфты ОК дает возможность реализовать распределенную компенсацию дисперсии вдоль линии. Поэтому использование режима управления дисперсией позволяет обеспечить увеличение РУ при фиксированном расстоянии между ОУ или увеличить расстояние между ОУ для ВОЛП с DDMS. Однако, для любой ВОЛП характерны свои особенности,которые должны быть учтены.

Заключение

В результате компьютерного моделирования РУ ВОЛП показана возможность реали- зации DDMS с включением компенсирующих ОВ в муфтах ОК в целях реконструкции линии для работы на более высоких скоростях.