Рекуррентные соотношения в динамической теории рентгеновской дифракции в латерально ограниченном кристалле
Автор: Колосов С.И., Пунегов В.И.
Журнал: Известия Коми научного центра УрО РАН @izvestia-komisc
Рубрика: Физико-математические науки
Статья в выпуске: 4 (24), 2015 года.
Бесплатный доступ
Получены рекуррентные соотношения, описывающие динамическую дифракцию рентгеновских лучей в латеральном кристалле. Разработан алгоритм вычислений кривых дифракционного отражения и карт распределения интенсивности рассеяния от кристалла прямоугольного сечения. Проведено численное моделирование рентгеновской Брэгг-Лауэ дифракции от кристаллов с разными латеральными размерами. Показано, что для толстых кристаллов с малыми латеральными размерами выполняется условие кинематической дифракции.
Динамическая теория дифракции, латерально ограниченный кристалл, рекуррентные соотношения
Короткий адрес: https://sciup.org/14992791
IDR: 14992791 | УДК: 548.732
Текст научной статьи Рекуррентные соотношения в динамической теории рентгеновской дифракции в латерально ограниченном кристалле
В настоящее время существуют разные подходы для описания динамической дифракции рентгеновских лучей в кристаллах [1, 2]. Динамическая тео- рия дифракции Дарвина [3, 4], основанная на методе рекуррентных соотношений, является наиболее простой и наглядной для решения конкретных задач рассеяния рентгеновских лучей и нейтронов от кристал- лов. Продолжительное время теория Дарвина не использовалась, поскольку имела некоторые ограничения по сравнению с теорией Эвальда-Лауэ [1]. Бори [5] первым сделал попытку описать эффект Бормана с использованием системы разностных уравнений Дарвина. В рамках этого подхода Безирганяном и Навасардяном [6] показано, что эффект Бормана зависит от размера отражающих плоскостей. С помощью подхода Дарвина были исследованы важные особенности динамического рассеяния, включая дифракцию в асимметричной геометрии Лауэ [7,8], многоволновое рассеяние [9, 10], а также свойства дисперсионной поверхности [7]. Рекуррентные соотношения, описывающие амплитуды проходящей и отраженной волны, применялись для исследования дифракции нейтронов в полиатомных кристаллах [11] и рассеянии света в жидких кристаллах [12]. Кроме того, процедура Дарвина была реализована в оптике слоистых сред [13].
Для исследования приповерхностных областей кристалла разработан формализм, получивший название crystal truncation rod (CTR) [14]. Схема динамической теории Дарвина была применена для исследования структуры поверхности кристалла методом CTR [15–19].
Яширо и Такахаши [20] исследовали коэффициенты отражения и прохождения рентгеновских лучей одной атомной плоскостью кристалла в общем случае для произвольной двумерной решетки Бра-вэ. Ими получены формулы для коэффициентов, отличающиеся от ранее опубликованных результатов Дурбина [21], но подобные формулам Бори [7]. Выражения коэффициентов отражения и прохождения, полученные Яширо и Такахаши [20], которые справедливы в случае произвольных направлений падающего и отраженного рентгеновского пучка, использованы в теории Дарвина для скользящей геометрии [22].
Известно, что теория Дарвина первоначально разработана для совершенного кристалла. Детальный анализ был выполнен для полубесконечно-го кристалла, включая эффекты преломления и поглощения [23]. Точное решение уравнений Дарвина для кристалла с произвольным числом отражающих плоскостей получено с использованием полиномов Чебышева [24]. Чен и Бхаттачаря [25] показали тождественность алгебраических уравнений Дарвина и дифференциальных уравнений Такаги [26] при переходе от модели массива дискретных атомных плоскостей к континуальной среде.
Отметим, что в природе идеальных кристаллов не существует. Поэтому особое внимание следует уделить работам, в которых формализм рекуррентных соотношений был обобщен для описания дифракции на искаженных структурах. Предприняты попытки для описания методом Дарвина дифракции рентгеновских лучей на кристаллах, решетка которых искажена под влиянием тепловых колебаний атомов [27] или из-за присутствия статистически распределенных дефектов [28]. Существенное влияние на дифракцию рентгеновских лучей оказывают деформации кристаллической решетки. Первая попытка численного моделирования рентгеновской ди- фракции на кристалле с линейным изменением параметра решетки с использованием уравнений Дарвина была выполнена Фицгеральдом и Дарлингтоном [29]. Результаты численных расчетов кривых дифракционного отражения данной работы согласуются с позже полученными аналитическими решениями [30, 31]. Прудников аналитически обобщил подход Дарвина к описанию рентгеновской дифракции в деформированных кристаллах. В частности, с помощью рекуррентных соотношений исследована дифракция в кристаллах, промодулированных поверхностной акустической волной [32], и в несовершенных гетероструктурах [33].
Рекуррентные соотношения, аналогичные уравнениям Дарвина, получены для описания дифракции в многослойных структурах, при этом коэффициенты отражения и прохождения от атомных плоскостей заменены на соответствующие коэффициенты от отдельных слоев [34, 35]. Такой подход был обобщен на случай многоволновой дифракции [36, 37], резко асимметричной [38] и скользящей геометрии [39].
Все отмеченные выше теории, использующие формулы рекуррентных соотношений Дарвина, разработаны для планарных структур с отражающими атомными плоскостями бесконечных размеров в латеральном направлении. В последние годы заметно возрастает интерес к дифракции рентгеновских лучей на латеральных структурах [40]. Разные методы динамической дифракции в рамках уравнений Такаги [26] были использованы для вычисления кривых дифракционного отражения от совершенных кристаллов прямоугольного сечения [41–43]. Кинематическая теория дифракции применялась для описания дифракции в искаженных кристаллах трапецеидального [44, 45] и произвольного поперечного сечения [46].
Цель данной работы состоит в разработке подхода Дарвина для исследования дифракции рентгеновских лучей в латеральных кристаллах. На примере кристалла прямоугольного сечения будут рассчитаны кривые дифракционного отражения и карты распределения интенсивности рассеяния (Reciprocal Space Maps (RSM)) в зависимости от ширины и толщины кристалла.
В теории Дарвина кристалл рассматривается как совокупность бесконечно тонких атомных плоскостей, отстоящих друг от друга на расстоянии d. В отличие от теории Лауэ [1], в модели Дарвина вся электронная плотность вещества сосредоточена в этих плоскостях. Амплитудные коэффициенты отражения и прохождения отдельной атомной плоскостью вычисляются с использованием теории дифракции Френеля [7, 20]. С другой стороны, переходя от дискретной модели Дарвина к континуальной среде [25] амплитудные коэффициенты отражения и прохождения атомной плоскостью можно выразить через Фурье-коэффициенты рентгеновской поляризуемости xg = -r 0 A 2 Fg/ ( nVc ) , где Fg - структурный фактор ( g = 0 , h, h ), A - длина волны падающего излучения Vc - объем элементарной ячейки, r 0 = e 2 / ( mc 2 ) -классический радиус электрона, где e , m – заряд и масса электрона, соответственно.
В результате коэффициенты, описывающие симметричные отражение и прохождение одной атомной плоскостью в рекуррентных соотношениях Дарвина, запишутся как q 0 = ndx 0 / ( A sin 9 b ) , q = ndXh/ ( A sin 9 b ) , - = ndx-h/ ( A sin 9 b ) , где 9 b — угол Брэгга. В этой статье мы рассматриваем случай σ -поляризации.
Рассмотрим плоскопараллельный кристалл, имеющий конечную толщину Lz = Nd , где N - число отражающих атомных плоскостей. Пусть на этот кристалл падает плоская рентгеновская волна под углом 9 = 9 b + Д 9 , где Д 9 - малое отклонение от точного брэгговского положения. Согласно теории Дарвина, выражения для амплитуд, прошедшей Tn и отраженной Sn рентгеновских волн для атомной плоскости с номером n , где отсчёт идёт сверху вниз, запишутся в виде следующих рекуррентных соотношений [1, 4]
Tn = (1 - iq 0) егфTn- 1 - iqe 2 iфSn, Sn = (1 - iq о) eiф Sn +i - iqTn.
Здесь Tn-1 , Sn+1 – соответствующие амплитуды волн, относящиеся к плоскостям с номерами n - 1 и n + 1, соответственно. Экспоненциальные множители в (1) учитывают набег фазы при распростране- нии рентгеновского поля между соседними атомными плоскостями. Поскольку поле может распространяться под углом, не равным углу Брэгга θB , то фаза Ф = (2nd/A) sin 9 при распространении рентгеновской волны от одной атомной плоскости до другой получает приращение, зависящее от угловой отстройки. Из-за малости отстройки Д9 фаза волны может быть представлена в виде ф = (2nd/A)cos 9bД9. Решение системы (1) с граничными условиями T0 = 1 и SN = 0
описывается следующими аналитическими решениями [47]:
Sn
B u 2 N u 1 n - u 1 N u 2 n
( Au i - 1) uN - ( Au 2 - 1) uN ’
T = ( Au 1 - 1) uN un - ( Au 2 - 1) uN un n ( Au 1 - 1) uN - ( Au 2 - 1) uN
---г 1 + (1 - iq о ) 2 e 2 ^ф + qqe 2 ^ф где u i = x i v x 2 - 1 , x = ,
1 , 2 , 2(1 - iq о) eW ’
A = (1 -iq0)егф, b = -iq. Из решения (2) при значениях n = 0 и n = N получаем амплитудные коэффициенты отражения S0 и прохождения TN рентгеновских волн от кристаллической пластины u2N - u1N
S 0 B ( Au i - 1) uN - ( Au 2 - 1) uN ’
T = _________ u 1 - u 2 _________
N ( Au 1 - 1) uN - ( Au 2 - 1) uN
Выражения (3) согласуются с точными аналитическими решениями, полученными ранее с использованием матричного подхода [24]. Учитывая, что для всех n в (2), unun = 1 , получаем
-iq
1 - (1 - iq о) е'1ф sin([ N - 1] arccos x ) / sin( N arccos x ) ’ (1 - iq 0) егф 2 Vx 2 - 1
sin( N arccos x ) - (1 - iq о) eiф sin([ N - 1] arccos x )
Формулы (4) совпадают с решениями, полученными ранее в работе [24]. Введя новый угловой пара-
1 - (1 - iqo)2e2^ф - qqe2^ф метр у = --------о _ .----—---и обозначив х =
2 qqeW arccos x, ^ = arccos у, амплитудные коэффициенты отражения и прохождения можно также записать в виде пт sin Nx
S о "V" q - s,n( Nx + N )“P( i' ’ ■
TN = v" N м exP(-N'^)■ sin( Nx + N)
Решения в виде (5) являются компактными и по форме совпадают с решениями для идеальной одномерной сверхрешетки [48].
Рекуррентные соотношения для кристалла прямоугольного сечения
Используем подход Дарвина для описания дифракции от латерально ограниченного кристалла. Обозначим ширину кристалла Lx ,аеетол-щину Lz (рис.1). Выберем следующую систему координат: ось x направлена вдоль входной поверхности кристалла, ось z – вглубь кристалла. Для простоты рассмотрим симметричную дифракцию Брэгга. Левая грань кристалла, на которую падает рентгеновская волна под углом θ к оси x , проходит через начало координат (рис.1).
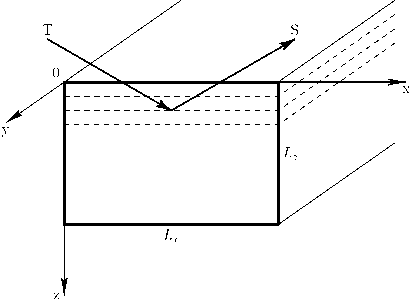
Рис. 1. Схематическое изображение рентгеновской дифракции на кристалле прямоугольного сечения.
Рассмотрим некоторый рентгеновский пучок, исходящий из начала координат. Этот пучок проходит расстояние d/ sin 9 и дифракционно отражается от ближайшей атомной плоскости. Проекция этого расстояния на латеральное направление равна Д x = d ctg 9 . Нанесем на атомные плоскости вдоль оси x разностную сетку с узлами xm = m Д x , в которых этот рентгеновский пучок частично отражается и частично проходит к следующей плоскости.
Пусть Tnm – значение амплитуды проходящей волны и Snm – соответствующее значение амплитуды отраженной волны непосредственно перед узлом ( m ; n ). Здесь индексы m и n нумеруют координаты узлов в горизонтальном и вертикальном направлениях, соответственно (рис.2). Число узлов решетки вдоль осей x и z , соответственно равное Mx и Nz , определяется размерами прямоугольного сечения кристалла Lx = Mx Д x и Lz = Nzd .
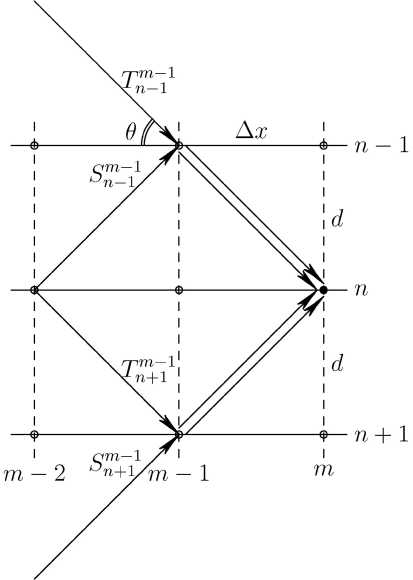
Рис. 2. Схематическое изображение отраженных и проходящих рентгеновских пучков в методе рекуррентных соотношений.
С учетом динамического рассеяния для отраженных S и проходящих T волн можно записать следующие рекуррентные соотношения:
m m- 1 m
Tn +1 — aTn + b 1 Sn
,
m m- 1 m- 1
Sn — aSn +1 + b 2 Tn +1 ,
где a — (1 - iq о) exp( гф 1) , b 1 — -iq exp( iф 1) , b 2 —
-iq exp(iф 1). Следует отметить, что мы используем здесь значения для q0, q и q, полученные для бес- конечного кристалла, что, безусловно, является при-
2 nd
X sin O b
ближением. Параметр ф 1 — i входящий в вы-
ражения для коэффициентов a и b1,2 , учитывает раз- ность фаз, возникающую при распространении рент- геновского пучка в кристалле от одного узла до другого. В системе алгебраических уравнений (6) индексы m и n нумеруют координаты узлов в горизонтальном и вертикальном направлениях, соответственно (рис.2).
Для кристаллической пластины бесконечного латерального размера распределение дифракционной интенсивности вблизи узла обратной решетки сосредотачивается в виде дельтаобразной линии в вертикальном направлении (вдоль вектора обратной решетки). Для латерального кристалла (то есть имеющего ограниченный размер в латеральном направлении) интенсивность рассеяния может распределяться вокруг узла обратной решетки как в вертикальном, так и в латеральном направлениях. Поэтому анализ распределения дифракционной интенсивности уместно проводить с использованием карт в обратном пространстве.
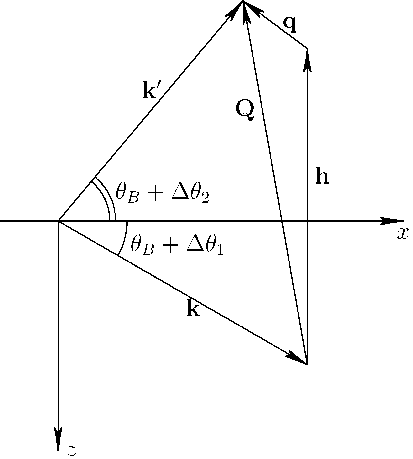
Рис. 3. Схематическое изображение рентгеновской дифракции в обратном пространстве.
Пусть на латеральный кристалл в направлении волнового вектора k падает рентгеновская волна под углом 0 1 — 0B + А0 1 к поверхности кристалла (рис.3.) Отраженная волна регистрируется в обратном пространстве в направлении вектора k′ под углом 02 — 0B + А02 к поверхности кристалла, причем |k| — |k‘I — 2п/X. Углы А0 1 и А02 задают малые угловые отклонение от точного условия Брэгга падающего и отраженного пучка, соответственно. Отклонение вектора дифракции Q — k‘ - k от конца вектора обратной решетки h определяется вектором q. Проекции qx и qz вектора q связаны с угловыми параметрами А0 1,2 следующими соотношениями qx — k sin 0b - (А01 - А02), qz — -k cos 0b - (А01 + А02).
Обозначив А0 1 — ш и А02 — е - ш, соотношения (7) преобразуются в выражения, используемые в трехкристальной рентгеновской дифрактометрии qx — k sin Ob - (2ш - е), qz — -k cos 0b - е, где ω и ε – параметры, определяющие угловое положение образца и кристалла-анализатора [49].
Рассмотрим алгоритм вычислений интенсивности рассеяния в зависимости от значений ( qx, qz ), или, что одно и то же, от углов θ 1 , 2 (см. (7)). Угловые параметры А 0 1 , 2 , согласно (7), связаны c проекциями вектора q следующими соотношениями: А 0 1 , 2 — ( ± 2 k cos O b ) - 1 ( qx ctg O b T qz ) •
Граничные условия
При прохождении и отражении рентгеновских лучей в кристалле происходит изменение фаз рентгеновских волн. За начало отсчета фазовых изменений выберем начало системы координат ( x — 0; z — 0 ), совмещенное с верхним левым углом прямоугольного сечения кристалла (рис.1). Для рентгеновских волн, падающих на левую боковую грань кристалла
( x = 0 ), разность хода растет с глубиной z по закону z sin 6 1 (рис. 4). Разность фаз для дискретных значений zn = nd вдоль вертикального направления равна Фn,in = (2 nd/X ) nd sin 6 1 . Граничное условие на левой боковой поверхности латерально ограниченного кристалла ( x = о ) запишется как T 0 = exp( фn,in ) и S^ = 0 , где n = 0 , 1 , 2 ,...,Nz . ’
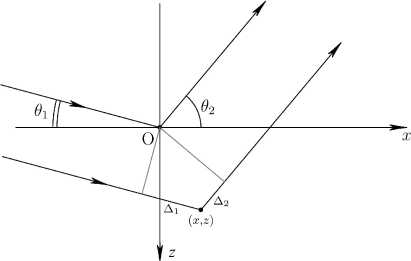
Рис. 4. К выводу фазовых изменений рентгеновских лучей в произвольной точке ( x ; z ) за счет возникновения разности хода A i = x cos 6 i + z sin 6 1 и A 2 = —x cos 6 2 + z sin 6 2 .
Для рентгеновских лучей, падающих на верхнюю поверхность латерального кристалла ( z = 0 ), разность хода растет с ростом координаты x как m A x cos 6 1 . Следовательно, имеет место изменение фазы падающей рентгеновской волны в горизонтальном направлении в зависимости от угла θ 1 . Граничное условие на верхней поверхности кристалла задается выражением T™ = exp( фт^ ) , где фm,in = (2 n/X ) m A x cos 6 1 , m = 1 , 2 ,..., Mx .
Для выходящей рентгеновской волны в направлении вектора k ‘ под углом 6 2 = 6B + 56 2 необходимо учитывать разность фаз фXm,ex = — (2 п/X ) m A x cos 6 2 на верхней поверхности кристалла (рис.4). Амплитуда рентгеновской волны, выходящей из правой боковой поверхности кристалла, приобретает фазовый набег фXm,ex = — (2 п/X )[ nd sin 6 2 — Mx A x cos 6 2 ] . Второе слагаемое в квадратных скобках этого выражения учитывает смещение правой грани кристалла на расстояние Lx = Mx A x от начала координат.
Поскольку в рассматриваемой геометрии (рис.1) дифракционная волна выходит из верхней и правой боковой грани кристалла, граничные условия для отраженной волны S на нижней и левой боковой гранях кристалла запишутся, соответственно, как SN z = 0 , sn = 0 .
Амплитудный коэффициент отражения рентгеновской волны от кристалла прямоугольного сечения находится суммированием рентгеновских волн:
S ( qx ,qz ) = S ( 6 1 ,6 2 ) =
M x N z
= 52 Sm ex P ( ivmex ) + 52 SM x ex P ( iФn,ex ) ,
где амплитуды рентгеновских волн S™ = Sm ( 6 1 ,6 2 ) и SM x = SnM x ( 6 1 ,6 2 ) находятся с использованием рекуррентных соотношений (6) и зависят от углов падения рентгеновского пучка θ 1 и угла регистрации θ 2 отраженной волны. Действительно, для падающей волны на границах кристалла амплитуды Tn = Tn ( 6 1) и
T o m = т™ ( 6 1) зависят только от угла падения. Однако в силу того, что фаза отраженной волны Фz,ex = Фz,ex ( 6 2 ) зависит от угла регистрации пучка, то в процедуре вычислений в рамках рекуррентных соотношений (6) амплитуды волн в направлении прохождения Tnm = Tnm ( 6 1 ,6 2) и отражения Snm = Snm ( 6 1 ,6 2) будут зависеть уже от двух углов или вертикальной и латеральной проекций вектора q . Поэтому решение (8) позволяет рассчитывать карты распределения интенсивности рассеяния в обратном пространстве (RSM). Кривые дифракционного отражения ( qx -сканы или CTR) могут непосредственно получены на основе решения (8) при условии 6 1 = 6 2 ( 2 ш = е ).
Численное моделирование
Численное моделирование кривых дифракционного (КДО, CTR) и RSM проводилось на основе решения (8) с использованием рекуррентных соотношений (6). Расчеты выполнены с использованием параметров, соответствующих (111) отражению CuK а 1 излучения от монокристалла германия. Для всех вычислений толщина латерального кристалла Lz соответствовала 10000 межплоскостных расстояний ( Lz = 10000 d 111 = 3 , 27 ф m ).
Латеральный размер кристалла выбирался с учетом числа узлов Nx вдоль горизонтального направления (Nx = 1000, 4000, 10000, 40000; что соответствует латеральным размерам Lx = 1 , 35 ф m , 5 , 39 ф m , 13 , 5 ф m , 53 , 9 ф m , ). Максимумы кривых дифракционного отражения нормировались на величину максимума кривой Дарвина для плоскопараллельной пластинки той же толщины.
Кривые дифракционного отражения, изображенные на рис.5, вычислялись на основе решения (8) для случая ш — 2 6 -сканирования ( 6 1 = 6 2 ). Поскольку в этом режиме сканирования полная разность хода A = A1 + A2 = 2 z sin 6 ( 6 = 6 1 = 6 2 ) (рис.4) не зависит от координаты x , то и полная разность фаз на верхней поверхности кристалла равна нулю: Ф^ = фX^,in + фX,ex = 0 . Отметим, что длина экстинкции на отражении (111) для полубесконечного кристалла кремния равна 0,67 µ m, полуширина дарвиновской кривой – 15,4 угл. сек. (см. [50] и адрес сайта ”X-Ray Server”).
Для малой латеральной ширины кристалла ( Lx = 1 , 35 ф m) кривая отражения соответствует кинематической дифракции (рис.5a). С увеличением латеральной ширины наблюдается постепенный переход к динамической дифракции (рис.5b,c), при этом толщинные осцилляции накладываются на профиль КДО даже в области полного отражения.
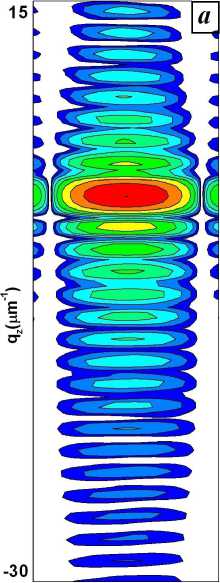
На рис.6. представлены RSM от кристаллов разной ширины. В случае кристалла с малым латеральным размером RSM имеет вид, отвечающий кинематической дифракции (рис.6a), и распределение дифракционной интенсивности соответствует известному закону [1]
I ( qx ,qz ) = S ( qx ,qz ) «
sin qx Lx / 2 qx Lx / 2
sin qz Lz / 2
qz Lz / 2
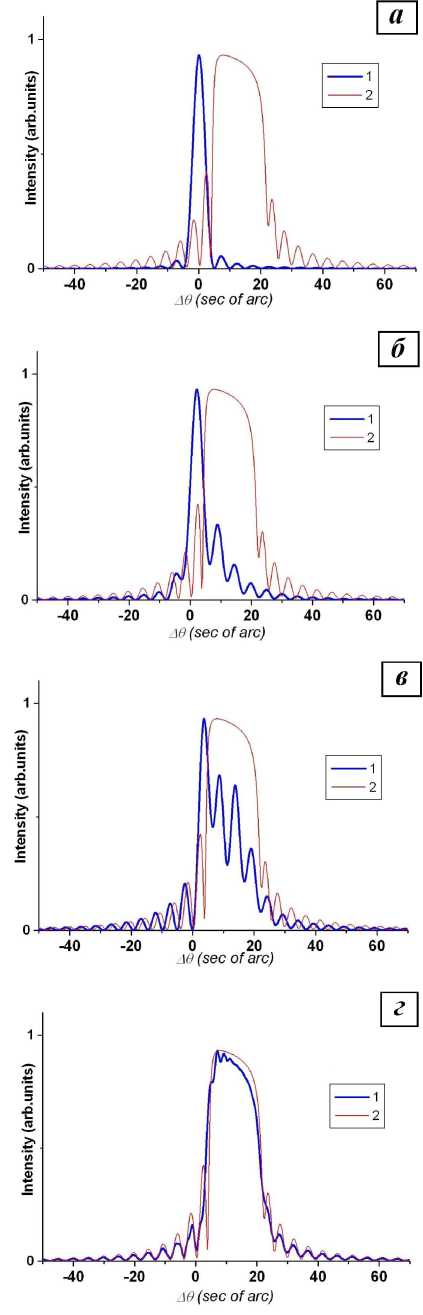
Рис. 5. Кривые дифракционного отражения для кристалла прямоугольного сечения толщиной L z = 3 , 27 ц m и разной ширины L x : a) 1,35 ц m; б) 5,39 ц m; в) 13,5 ц m; г) 53,9 ц m. Для сравнения тонкой красной линией 2 изображена кривая дифракционного отражения от плоскопараллельной пластинки ( L x = го ) той же толщины L z .
■5 qx(pm"1) 5
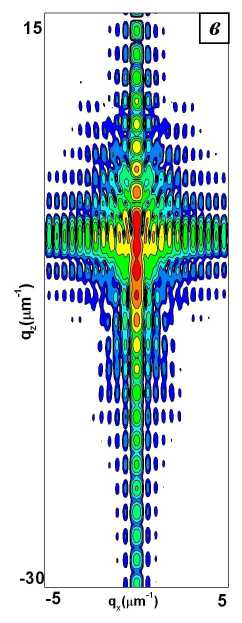
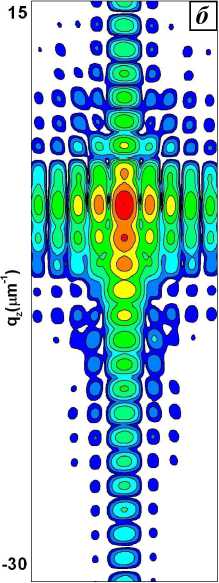
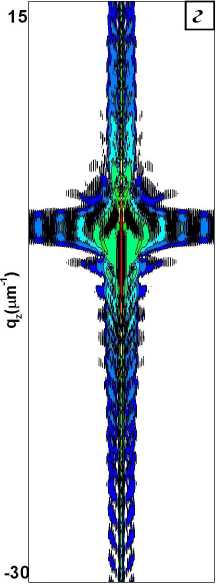
Рис. 6. RSM от кристалла прямоугольного сечения толщиной L z = 3 , 27 ц m и разной ширины L x : a) 1,35 ц m; б) 5,39 ц m; в) 13,5 ц m; г) 53,9 ц m.
5 qx(grn'1) 5
5 qx(^rn"1) 5
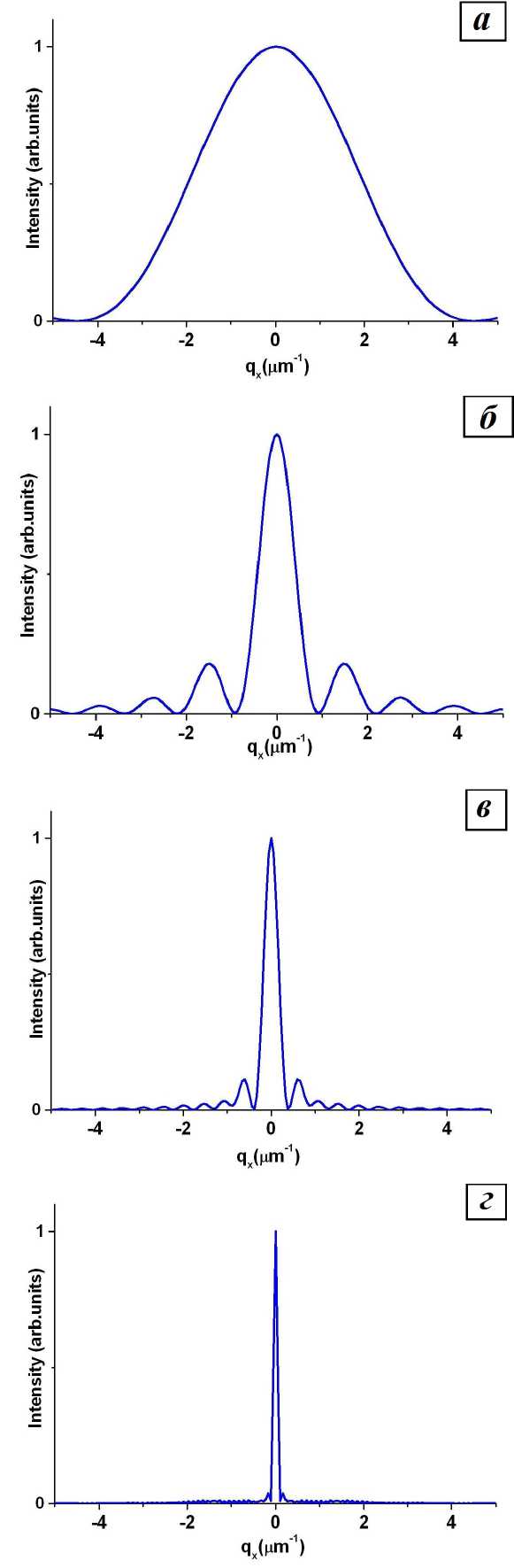
Рис. 7. Кривые качания ( q x -сканирования) от кристалла прямоугольного сечения толщиной L z = 3 , 27 ц m и разной ширины L x : a) 1,35 ц m; б) 5,39 ц m; в) 13,5 ц m; г) 53,9 ц m.
С увеличением латерального размера кристалла угловое распределение интенсивности рассеяния на RSM в qx -направлении становится все более узким, уменьшается также период латеральных осцилляций. Этот период обратно пропорционален
латеральному размеру кристалла. На это непосредственно указывают qx -сканы RSM для значений qz , соответствующих максимальному значению дифракционной интенсивности (рис.7).
Результаты полностью согласуются с теми, что получены решением данной задачи путем интегрирования уравнений Такаги-Топена.
Заключение
Таким образом, мы показали, что теория Дарвина, в основе которой лежат алгебраические рекуррентные соотношения, в геометрии Брэгга может описывать не только дифракцию на плоскопараллельных пластинках, но и на латерально ограниченных кристаллах. Рассмотренный подход является не только наиболее простым и наглядным, но и требует существенно меньших временных затрат на вычисления кривых дифракционного отражения и RSMs. Поскольку в настоящее время латеральные структуры, создаваемые методами литографии и электрохимического травления, широко применяются в приборах микро- и оптоэлектроники, энергонезависимых запоминающих устройствах (nonvolatile memory devices), элементах рентгеновской оптики и т.д., разработанный подход может быть эффективно использован для неразрушающего рентгенодифракционного анализа таких материалов.
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 13-02-00272-а).
Список литературы Рекуррентные соотношения в динамической теории рентгеновской дифракции в латерально ограниченном кристалле
- Authier A. Dynamical Theory of X-Ray Diffraction. New York: Oxford University Press, 2001. 661 p.
- Pietsch U., Holy V., and Baumbach T. High resolution X-ray scattering: from thin films to lateral nanostructures. 2nd edition. New York: Springer-Verlag, 2004.
- Darwin C.G. The Theory of X-Ray Reflexion//Philos. Mag. 1914. Vol. 27. P. 315-333.
- Darwin C.G. The Theory of X-Ray Reflexion. Part II//Philos. Mag. 1914. Vol. 27. P. 675691.
- Borie B. The Theory of the Borrmann Effect in Terms of Difference Equations//Acta Cryst. 1966. Vol. 21. P. 470-472.
- Безирганян П.А., Навасардян M.A. Теория эффекта Бормана для конечного кристалла//Изв. АН Арм. ССР. Физика. 1969. Т. 3. С. 269274.
- Borie B. The Darwin dynamical theory of x-ray diffraction//Acta Cryst. 1967. Vol. 23. P. 210216.
- Кузнецов A.B., Фофанов А.Д. Дарвиновская теория рассеяния идеальными кристаллами в асимметричном положении//Известия ВУЗов. Физика. 1970. № 10. C. 12-18.
- Кузнецов A.B., Фофанов А.Д. О тождественности методов Дарвина и Эвальда-Лауэ (обобщение метода Дарвина на любое число сильных волн)//Известия ВУЗов. Физика. 1972. № 4. C. 108-113.
- Игнатович В.К. Многоволновой алгебраический метод Дарвина в динамической теории дифракции//Кристаллография. 1992. Т. 37. № 5. С. 1100-1112.
- Игнатович В.К. Алгебраическое описание динамической дифракции на многоатомных идеальных кристаллах//ЖЭТФ. 1990. Т. 97. № 5. C. 1616-1625.
- Chandrasekhar S., Srinivasa Rao K. N. Optical rotatory power of Liquid crystals//Acta Cryst. 1968. Vol. A24. P. 445-451.
- Dub P., Litzman O. The Darwin procedure in optics of layered media and the matrix theory//Acta Cryst. 1999. Vol. A55. P. 613-620.
- Robinson I.K. Crystal truncation rods and surface roughness//Phys. Rev. B. 1986. Vol.33. No. 6. P. 3830-3836.
- Caticha A. Diffraction of x rays at the far tails of the Bragg peaks. II. Darwin dynamical theory//Phys. Rev. B. 1994. Vol. 49. No. 1. P. 33 38.
- Durbin S. M, Follis G.C. Darwin theory of heterostructure diffraction//Phys. Rev. B. 1995. Vol. 41. №15. P. 10127-10133.
- Nakatani S., Takahashi T. Dynamical treatment of x-ray reflection from crystal surface//Sur. Sci. 1994. Vol. 311. P. 433-439.
- Takahashi T., Nakatani S. Dynamical theory of X-ray diffraction for the study of crystal surfaces//Surface science, 1995. Vol. 326. P.347-360
- Takahashi T., Yashiro W., Takahasi M., Kusano S. Effect of surface structure on crystal-truncation-rod scattering under the Bragg condition//Physical Review B. 2000. Vol. 62. P. 3630-3638.
- Yashiro W., Takahashi T. X -ray diffraction from an atomic plan//Acta Cryst. 2000. Vol. A56. P. 163-167.
- Durbin S. M. Darwin spherical-wave theory of kinematic surface diffraction//Acta Cryst. 1995. Vol. A51. P. 258-268.
- Yashiro W., Ito Y., Takahasi M, Takahashi T. Darwin’s theory for the grazing incidence geometry//Surface science. 2001. Vol. 490. P. 394-408.
- Prins J. A. Die Reflexion von Rontgenstrahlen an absorbierenden idealen Kristallen//Zeitschrift fur Physik. 1930. Vol. 63. No. 7-8. P. 477-493.
- Perkins R.T., Knight L.V. An exact analytic solution of Darwin’s difference equations//Acta Cryst. 1984. Vol. A40. P. 617-619.
- Chen, Y.C. Bhattacharya, P.K. Determination of critical layer thickness and strain tensor in lnxG&1-xAs/GaAs quantum-well structures by x-ray diffraction//Journal of Applied Physics. 1993. Vol. 73. No. 11. P. 7389-7394.
- Takagi S. A Dynamical theory of diffraction applicable to crystals with any kind of small distortion//Acta Cryst. 1962. Vol. 15. № 12. P. 1311-1312.
- Chung J.S., Durbin S.M. Temperature-dependent X-ray dynamical diffraction: Darwin theory simulations//Acta Cryst. (1999). Vol. A55. P. 14-19.
- Li M., Ress H., Gerhard T., Landwehr G., Cui S.F., Mai Z.H. A semi-kinematic approach to x-ray diffraction of real crystals with small defects//J. Appl. Phys. 1997. Vol. 81. P. 2143-2147.
- Fitzgerald W.J., Darlington C.N.W. A numerical study of the dynamical theory of scattering from a distorted crystal//Acta Cryst. 1976. Vol. A32. P. 671-672.
- Kolpakov A.V., Punegov V.I. X-ray diffraction in a crystal with a linear lattice parameter variation//Solid State Communications. 1985. Vol. 54. No. 7. P.573-578.
- Punegov V.I., Vishnjakov Yu.V. Dynamical theory of X-ray diffraction from damaged epitaxial layers with constant strain gradient//J. Phys. D: Appl. Phys. 1995. Vol. 28. No. 4A. P. A184-A188.
- Prudnikov I.R. Darwin’s approach to X-ray dynamical diffraction in distorted crystals//Acta Cryst. 1998. Vol. A54. P. 1034-1036.
- Prudnikov I.R. X-Ray Diffraction in Distorted Crystals and Imperfect Multilayered Structures. A Theoretical Approach Based on Resursion Equations//Phys. Stat. Sol. (b). 2000. Vol. 217. P. 725-735.
- Bartels W.J., Hornstra J., Lobeek D.J.W. Acta Crystallogr., Sect. A: Found. Crystallogr. 42, 539 (1986).
- Belyaev Yu.N., Kolpakov A.V. On the theory of x-ray diffraction in a perfect crystal with distorted surface layer//Phys.Stat.Sol.(a). 1983. Vol. 76. P. 641-645.
- Ladanov A.V., Punegov V.I. A new approach to the problem of multiple X-ray diffraction in multilayer crystals//Twelfth Europen Crystallographic meeting. Moscow, USSR, August 20-29, 1989/Collected Abstracts. Moscow. 1989. Vol. 3. P. 137.
- Punegov V.I. X-ray diffraction from multilayer structures with statistically distributed microdefects.//Physica status solid (a). 1993. Vol. 136. No. 1. P. 9-19.
- Пунегов В.И., Ладанов А.В. Теория дифракции рентгеновских лучей в многослойных кристаллах в условиях полного внешнего отражения//Поверхность. Физика. Химия. Механика. 1990. № 4. С. 45-50.
- Пунегов В.И., Ладанов А.В. О дифракции рентгеновских лучей на многослойной пленочной структуре в скользящей геометрии//Журнал технической физики. 1989. Т. 59. № 11. С. 188-189.
- Lee K, Yi H, Park W.-H, Kim Y.K. Baik S. Lateral size effects on domain structure in epitaxial PbTiO3 thin films//J. Appl. Phys. 2006. Vol. 100. P. 051615 (1-10).
- Колосов С.И., Пунегов В.И. Методы численного интегрирования уравнений Та-каги-Топена для кристалла прямоугольного сечения//Кристаллография. 2005. Т. 50. Вып. 3. С. 401-406.
- Olekhnovich N.M., Olekhnovich A.I. Prirnary Extinction for Finite Crystals. Square-Section Parallelepiped//Acta Cryst. 1978. Vol. A34. № 2. P.321-326.
- Thorkildsen G., Larsen H.B. X-ray diffraction in perfect crystals. Rocking curves//Acta Cryst. 1999. Vol. A55. P. 840-854.
- Пунегов В.И., Колосов С.И., Павлов К.М. К теории дифракции рентгеновских лучей на латеральном кристалле с упруго изогнутыми атомными плоскостями//Письма в ЖТФ. 2006. T.32. Вып. 18. C. 65-72.
- Пунегов В.И., Колосов С.И. Теория дифракции рентгеновских лучей на неидеальном кристалле трапецеидального сечения//Кристаллография. 2007. Т. 52. № 2. С. 215-222.
- Пунегов В.И., Максимов А.И., Колосов С.И., Павлов К.М. К расчету дифракции рентгеновских лучей от многослойных латеральных кристаллических структур произвольных композиционного состава и формы//Письма в ЖТФ. 2007. Т. 33. Вып. 3. C. 64-71.
- Пунегов В.И. Рентгеновская дифракция на полупроводниковой сверхрешетке с микродефектами//Письма в ЖТФ. 1992. Т. 18. № 4. С. 66-70.
- Vardanyan D.M., Manoukyan H.M., Petrosyan H.M. The dynarnic theory of x-ray diffraction by the one-dirnensional ideal superlattice. I. Diffraction by the arbitrary superlattice//Acta Cryst. 1985. Vol. A41. P. 212-217.
- Iida A., Kohra K. Separate rneasurernents of dynarnical and kinernatical x-ray diffractions frorn silicon crystals with a triple crystal diffractorneter//Phys. Stat. Sol. (a). 1979. Vol. 51. P. 533-542.
- Stepanov S., Forrest R. Fitting dynarnical X-ray diffraction data over the World Wide Web//Journal of Applied Crystallography. 2008. Vol. 41. P. 958962, http://sergey.grnca.aps.anl.gov/.


