Рекурсивное миграционное преобразование радарограммы в системе подповерхностной радиолокации
Автор: Борзов Андрей Борисович, Лабунец Леонид Витальевич, Зотов Алексей Владимирович, Копейкин Роман Евгеньевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 4-1 т.18, 2016 года.
Бесплатный доступ
Предложен эффективный в вычислительном отношении рекурсивный алгоритм миграционного преобразования радарограммы в системе подповерхностной радиолокации. Алгоритм основан на анализе восходящего и нисходящего волновых полей в последовательных слоях зондируемой неоднородной среды с помощью комбинации миграционных отображений Столта и Газдага.
Подповерхностная радиолокация, цифровая обработка сигнала, миграционное преобразование
Короткий адрес: https://sciup.org/148204642
IDR: 148204642 | УДК: 621.376.3
Текст научной статьи Рекурсивное миграционное преобразование радарограммы в системе подповерхностной радиолокации
Одним из популярных методов цифровой обработки геофизической информации, получаемой в результате зондирования объектов исследования сверхкороткими видеоимпульсами порядка нескольких сотен пикосекунд, является метод обратного миграционного преобразования радарограммы. Этот метод отображает пространство изображения измеренных данных на пространство геофизической модели зондируемой области. Кроме того, метод обеспечивает увеличение отношения сигнал / шум и горизонтальной разрешающей способности георадара. Миграционное преобразование успешно применяют при решении задач обнаружения, определения местоположения и идентификации объектов искусственного и естественного происхождения, находящихся под слоем диэлектрического материала в виде почвы, скальной породы, воды, льда и т. п.
Для повышения помехоустойчивости метода, как правило, выполняют предварительную обработку экспериментальных измерений с целью выделения информативных сигналов, их интерпретации и последующего анализа многослойной структуры среды, рассеивающей электромагнитные волны (ЭМВ). Такого рода задачи имеют самостоятельное значение при мониторинге толщины ледовых покровов, качества дорожных покрытий, взлетно-посадочных полос, мостов, железнодорожного полотна и т. п.
ДИСКРЕТНАЯ МОДЕЛЬ ВОЛНОВОГО ПОЛЯ
Натурные измерения выполняют с помощью однопозиционного георадара, излучатель и приемник которого практически совмещены в пространстве. Регистрируемый массив данных описывает рассеянное средой трехмерное волновое поле f ( t, x, z ), где t – время, x и z – пространственные координаты, направленные вдоль и в глубину исследуемой поверхности. Соответствующую дискретную модель поля, заданного на ортогональном растре, удобно представить в виде трехмерной матрицы
f ( n1, n2, n3 ) = f ( n1 Δ t, n2 Δ x, n3 Δ z ), 0≤ ni ≤ Ni -1, i = 1,2,3. (1)
Здесь Δ t и Δ x , Δ z – интервалы временн о й и пространственной дискретизации, согласованные по теореме отсчетов Котельникова – Шеннона [1, с. 58] с верхними граничными частотами Wi , i = 1,2,3 (частотами Найквиста).
Фурье-спектр поля вычисляют по формуле Φ(ω,kx,kz)= ∞∫dt ∞∫dx ∞∫f(t,x, z)exp(- jωt- jkxx - jkzz)dz,(2) -∞ -∞ -∞ если ω ≤W1, kx ≤W2, kz ≤W3 и Φ(ω,kx,kz)≈0 в противном случае. Здесь, в отличие от геофизической транскрипции [2, с. 33; 3, с. 89], принята стандартная радиофизическая форма записи непрерывного преобразования Фурье. Также следует отметить, что ширина полосы частот спектра (2) определяется значениями 2Wi, i = 1,2,3.
Если выполняются ограничения ∆t ≤ π/ W1 , ∆x≤π/W2 , ∆z≤π/ W3 , то периодическое продолжение спектра (2) в частотном пространстве (ω, kx , kz), как результат процедуры дискретизации данных (1), не приводит к эффекту наложения спектральных копий [1, с. 57]. В случае равенств в указанных выше ограничениях опорная область спектра (2) и ее периодические копии образуют плотную упаковку в частотном пространстве, что обеспечивает наименьшую плотность узлов ортогонального растра в исходном пространстве (t, x, z). Это, в свою очередь, позволяет реконструировать значения поля
N i - 1 N 2 - 1 N з - 1
~ ( t , x , z ) = E E E f ( n 1 , n 2 , n 3 ) ф ( t - n 1 A t , x - n 2 Д x , z - n 3 Д z ) n 1 = 0 n 2 = 0 n з = 0
9 (ю , kx|z ) = J
4 ю 2
V v ( x , u )
k x
у/2
du ,
где R ( ю , k x ) = F ( ю , k x\ z = 0 ) - спектр Фурье
с помощью оптимальной интерполирующей
функции
ф ( t , x , z ) =
sin ( W 1 1 ) sin ( w 2 x ) sin ( w 3 z )
W 1 t W 2 x W 3 z
с нулевой или приемлемо малой ошибкой e ( t , x , z ) = ~ ( t , x , z ) - f ( t , x , z ) .
МИГРАЦИОННОЕ ПРЕОБРАЗОВАНИЕ
радарограммы.
В соответствии со свойствами преобразования Фурье полученное решение показывает, что волновое поле f ( t , x , z ) на глубине z получают с помощью сдвига гармоник радаро-граммы r ( t , x ) = f ( t , x , z = 0 ) на величину накопленной фазы о ( ю , kx | z ) . Миграционное преобразование методом фазового сдвига [2, с. 42; 3, с. 107] предполагает вычисление обратного непрерывного преобразования Фурье с помощью дисперсионного соотношения (6). С учетом тождества exp ( j ю t ) = 1 для t = 0 получим
В ряде работ [4, 5] отмечалось, что наиболее эффективные алгоритмы миграции сигналов, сформированных элементарными отражателями однородной среды, основаны на суммировании амплитуд сигналов каждого рассеивателя вдоль дифракционной гиперболы [6 - 8] или методе Столта восстановления геофизического изображения зондируемой среды [2, с. 44; 3, с. 95]. Указанные алгоритмы устойчивы к шумам измерений, не вносят значимых интерференционных искажений в процессе преобразования и требуют относительно небольших вычислительных затрат.
Радарограмма представляет собой двумерное сечение матрицы (1) r(t, x) = f (t, x, z = 0), т. е. содержит результаты экспериментальных измерений поля на поверхности среды z = 0. Миграционное преобразование радарограммы r(t, x) позволяет восстановить волновое поле в вертикальном разрезе среды p(t, z) = f (t = 0, x, z) для начального момента времени t = 0. Основой
W 2
Р ( x , z ) = f ( t = 0, x , z ) = J R ( k x , z ) eXP { jkxx } dkx ,
- W 2
W 1
R~ ( k x , z ) = J R (ю , k x ) eXP { j 0(ю , k x l z )} d ю . (8)
- W 1
Иными словами, волновое поле в вертикальном разрезе среды p ( x , z ) представляет собой обратное непрерывное преобразование Фурье спектрограммы R ~ ( k x , z ) по вол -новому числу kx . Спектрограмма, в свою очередь, является результатом фазовых сдвигов спектра Фурье радарограммы для текущих глубин z и последующего интегрирования по частоте ю .
ОТОБРАЖЕНИЕ СТОЛТА
такого рода реконструкции является скалярное волновое уравнение [3, с. 105] в частотном пространстве ( ю , k x )
dF ( ю , kAz ) ( x 3 = jkzdz .
F ( ю , kx|z ) J z
Здесь F ( ю , kx\z ) - спектр Фурье двумерного сечение волнового поля f ( t , x , z ) для фиксированного значения заглубления z > 0; волновое число k z удовлетворяет соотношению
В однородной среде скорость распространения волнового фронта не зависит от координат вертикального разреза v ( x , z ) = v . В этом случае накопленная фаза (7) увеличивается линейно в зависимости от глубины
б( ю
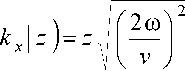
k x 2
= k z ( ю , k x ) z .
k x + k z
4 ю 2
;
v 2 ( x , z )
Соответствующее интегральное преобразование Фурье, основанное на дисперсионном соотношении (6), приобретает вид
W 2 W 1
p ( x , z ) = J dk x J R ( to , k x ) exp { jk.x + jkz ( to , k x ) z } d ю .
- W 2 - W 1
v ( x , z ) - скорость распространения ЭМВ в среде. Решение указанного выше однородного линейного дифференциального уравнения с разделяющи-
мися переменными имеет вид дисперсионного
Замена переменных в полученном равенстве с помощью подстановки ю = v^k x; + k z /2 приводит к обратному преобразования Фурье
W 2 W 3
p ( x , z ) = J ( kx , kz ) J dk x J R { ю ( kx , kz ) , kx } exp { jk x x + jkzz } dk z .
- W 2 - W 3
соотношения
F (ю , k x
z ) = R ( ю , k x ) exp { j 9 ( ю , k x| z )} , (6)
для спектра R( ю , k x ) радарограммы, рассчитанного на нелинейном растре { ю ,( k x , k z ), k x }. Здесь
J ( k x , k z ) =
vkz
V k x + k z
якобиан преобразования. Последовательность вычислений, реализующая алгоритм миграционного отображения Столта, представлена в Приложении 1. Результаты применения алгоритма для тестового изображения, хранящегося в базе данных на сайте [9] обучающего курса профессора Guy G. Drijkoningen факультета гео-инженерных технологий университета Дельфта, иллюстрирует рис. 1. Вычисления выполнялись для следующих параметров: v = 1550 м/с , K t = 0,004 с , K x = 50м , K z = 6,2 м , N 1 = 1001, N 2 =141, N 3 =1001. В данном примере алгоритм Столта отображает дифракционные гиперболы исходных сейсмических данных в два точечных источника волнового поля геофизического разреза однородной среды.
С методической точки зрения радиофизическая интерпретация нелинейного отображения Столта состоит в преобразовании радарограммы двумерным фильтром. Передаточная функция такого фильтра в частотном пространстве ( ю , k x ) имеет вид [2, с. 34; 3, с. 107]
H ( ю , kx\z ) = exp < jz
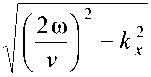


б)
где фиксированное значение заглубления z > 0 трактуется как параметр.
ОТОБРАЖЕНИЕ ГАЗДАГА
Рис. 1. Миграционное преобразование Столта: а – исходные данные; б – мигрированные данные
К9 ( ю , kx | z ) = 9 ( ю , k x z + К z ) -
Рассмотрим многослойную среду, в которой скорость распространения ЭМВ не зависит от горизонтальной координаты x и изменяется локально постоянно от слоя к слою, т. е.
V 1 , 0 < z < z 1
-9 ( ю , kx\z ) = k z ( ю , kx ) K z ,
k z ( ю
kx ) =
^
2 ю
.v (z)
k x 2 .
v (x, z ) = v (z ) = <
V 2 ,
z 1
< z < z 2
, (9)
V L , z L - 1 < z < z L
где Vl и zl – скорость распространения ЭМВ и заглубление нижней границы l -ого слоя, l = 1, 2, …, L .
Изменение скорости распространения зондирующего излучения в среде естественным образом учитывает миграционное отображение Газдага [2, с. 42]. В рамках этого подхода дисперсионное соотношение (6) представляют в рекуррентной форме
F ( ю , k x z + K z ) = F ( ю , k x z ) exp { j K9 ( ю , k x z )} ,
где с учетом формулы (7) фазовый сдвиг Ko ( ю , kx\z ) спектра Фурье нисходящего волнового поля при переходе от заглубления z к заглублению z + K z имеет вид
Алгоритм Газдага прямого отображения по нисходящим волнам r ( t, x ) ^ p ( x, z ) , представлен в Приложении 2.
Миграционное преобразование радаро-граммы с помощью алгоритма фазового сдвига предполагает наличие априорной информации о распределении скорости распространения ЭМВ по глубине. Такого рода информацию получают на этапе предварительной обработки данных с помощью современных методов структурного анализа радарограммы [10].
Результаты применения алгоритма для сейсмических измерений, хранящихся в базе данных на сайте [9], демонстрирует рис. 2. Вычисления выполнялись для следующих параметров: К t = 0,004 с , K x = 20 м , K z = 4 м , N 1 = 3001, N 2 = 1024, N 3 = 1046. Представленное на рис. 3 локально постоянное распределение скоростей (9) по L = 14 слоям среды загружалось из отдельного файла базы данных [9].


Рис. 2. Миграционное преобразование Газдага: а – исходные данные; б – мигрированные данные
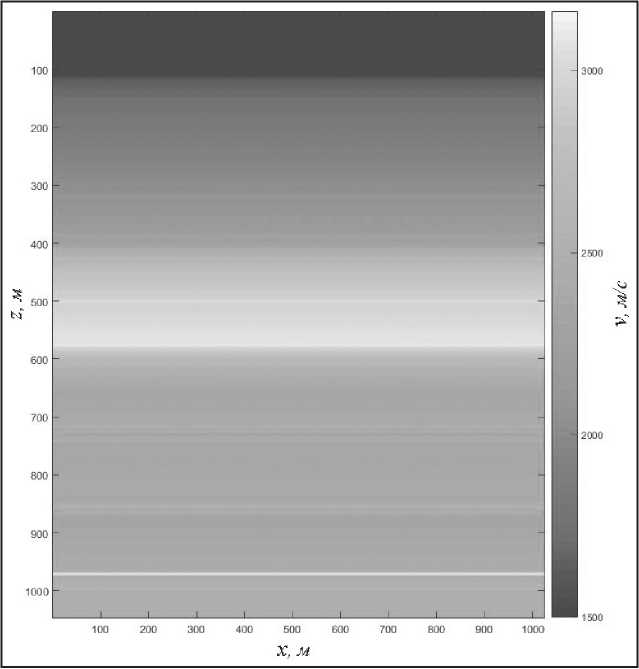
Рис. 3. Распределение скорости распространения волн по слоям неоднородной среды
РЕКУРСИВНОЕ ОТОБРАЖЕНИЕ СТОЛТА
Вычисление интеграла (7) с учетом модели (9) дает кусочно-линейную зависимость накопленной фазы от глубины
б( Ю , kx\z ) =
k 9 ) ( ю , k x ) z , z 0 < z < z 1
k Z 2 )( Ю , k x ) z -A6 2 )( Ю , k x ) , z 1 < z < z 2
k ZL )( Ю , k x ) z - E A9 ( l + 1 Iю , k x ) , z L - 1 < z < zL , l = 1 ,
(12) где z 0 = 0, A6 ( 1 + 1 ) ( o , k x ) = { k <1 + 1 ) ( o , k x ) - k zl ) ( ® , k x ) } z , – коррекция набега фазы за счет изменения скорости распространения ЭМВ в среде. Значения волнового числа kz находят по формуле (11) для скорости v ( z ) = V l .
Кусочно-линейная зависимость (12) позволяет представить дисперсионное соотношение (6) в следующем виде
F (o , kx\z )= B (° , kx\z1 -1 ) exp {jk Z )(ю , kx ) z } , l = 1, 2, …, L. (13)
Здесь спектр Фурье B ( ю , kx | z l - 1 ) восходящего волнового поля для верхней границы z , - 1 текущего l -ого слоя вычисляют рекурсивно по слоям среды. В первом слое z 0 < z < z 1 спектр восходящего волнового поля на поверхности среды представляет собой радарограмму
B (ю , kx\z о ) = R (ю , k x ) .
В последующих слоях z , - 1 < z < z , , l = 2, ..., L спектр восходящих волн на глубине z , — 1 рассчитывают по предыдущим спектральным оценкам нисходящего поля
B ( ю , k x z l - 1 ) =
= F (ю , kx|zl - 1 ) exP { - jkzl ) ( ю , kx ) zl - 1 } . (14)
Очевидно, что рекурсия спектральных оценок нисходящих и восходящих волн позволяет последовательно от слоя к слою применять эффективный в вычислительном отношении алгоритм миграции Столта. Рекурсивную по слоям модификацию этого алгоритма содержит Приложение 3.
Анализ рекурсии Столта выполнялся для тестовой радарограммы в виде суммы двух дифракционных гипербол и гауссовского шума (рис. 4.а). Скорости распространения волн (равные тангенсам углов наклона асимптот) в двух слоях среды принимали значения 1 и 2 соответственно. Миграцию гипербол в точечные источники волнового поля геофизического разреза двухслойной среды иллюстрирует рис. 4.б.
Результаты тестирования рекурсивного алгоритма Столта демонстрируют экономию вычислительных затрат по сравнению с алгоритмом Газдага пропорциональную количеству слоев среды.

a)

Рис. 4. Рекурсивное миграционное преобразование Столта: а – исходные данные; б – мигрированные данные
Приложение 1. Миграционное преобразование Столта.
Шаг 1 . Вычислить двумерное дискретное преобразование Фурье (ДПФ) радарограммы r ( n 1, n 2 ) = r ( n 1 A t, n 2 A x ) по времени t и координате x .
n 1 - 1 n 2 - 1 ^ 2 п 2 п |
R ( m 1, m 2 )= E E r( n 1, n 2 ) exp I-j — n 1 m 1 - j^Tn 2 m 2 I , n 1= 0 n 2 = 0 I N1 N 2 J
(П.1)
где R ( m 1, m 2 ) = R ( m 1 Ao , m 2 A kx ) , 0 < m i < N i - 1 , i = 1,2 ,
- дискретная модель спектра Фурье R(Q, kx), рассчитанная на ортогональном растре с интер- валами
дискретизации
A 2 W1
Ao= =
N ! - 1 ( N ! - 1 ) a t
,
Л/ 2 W 2
A kx == x N2 -1 (N2 -1 )ax
2 п в частотном домене 0 1 A t 2 л 0 < kr< 2W. = — x2 A x . Шаг 2. Выполнить дискретизацию пространственной частоты kz в интервале 0 < kz< 2 W3 = 2 п/ Az с шагом A k z 2 W 3= 2 п N3 -1 (N3 -1)Az" (П.2) Отобразить узлы ортогонального растра (m2Akx, m3Akz) на пространство частот to(m2,m3), m2Akx} с помощью нелинейного соотношения (5). to( m 2, m з )= 2J(m2Akx)2+ (mзAkz)2.(П.З) Приложение 2. Миграционное преобразование Газдага. Шаг 1. Вычислить по формуле (П.1) двумерное ДПФ R(m1, m2) радарограммы. Шаг 2. Инициализировать цикл по глубине z. n3= 0, Az = zL[ (N3-1). Вычислить значения дискретной модели волнового поля на поверхности объекта локации z = 0, P(n2, n3 )= P(n 2 Ax, n3Az )= r(0, n 2 Ax)= r(0, n 2 ). Шаг 3. Цикл по глубине z. n 3 = n 3 +1, z = z + A z. Преобразовать частоты to ( m 2, m 3) к основно-„ 2 п му домену 0 < Q < — ДПФ радарограммы A t Шаг 4. Инициализировать цикл по волновому числу kx . q(m2 ,m3 m2, m3)}2п, m 2 = -1, A k = 2W2 = 2п . _ x N 2 -1 (N 2 -1 )A x ’ x x At 0 < mt< Ni -1, i = 2,3, (П.4) Шаг 5. Цикл по волновому числу kx. m 9 = m 9 +1, k T= kT + A k „. xx x где функция {a}b означает остаток от деления величины a на целое число порций b. Шаг 3. Выполнить интерполяцию отсчетов ДПФ радарограммы на нелинейном растре { q(m2 ,m3), m2 Akx} Обнулить начальное значение спектрограммы R( m 2 , n 3 )= R~( kx , z )= 0. Шаг 6. Инициализировать цикл по частоте to. 2 W1 2 п mi = 0, Ato = ~—-= , to = 0. 1 N 1 -1 (N 1 -1 )A t R{ Q (m2,m3), m2 N1-1 , Z R ( m 1=0 m1,m2 )p{q( m2, m3 - m 1Ato В соответствии со свойством дуальности ДПФ [1, с. 93] оптимальная интерполирующая функция p(Q) в частотном пространстве имеет вид, аналогичный интерполирующей функции (4) в исходном пространстве p(Q)= sin(тr Q / 2 ) _ sin (п Q / Ato) тRQ/2 nQ/Ato , (П.5) где тR = (N 1 - 1) At - длительность отраженных сигналов радарограммы. Шаг 4. Вычислить оценку ДПФ P ( m2, m3) волнового поля p(x, z) в вертикальном разрезе среды с помощью операции масштабирования P(m2, m3) = vm 3 A kz (m 2 Akx)2 + (m 3 Akz)2 Q(m2,m3), m2 Шаг 5. Реконструировать дискретную модель волнового поле в вертикальном разрезе среды с помощью обратного ДПФ по волновым числам kx и kz. P (n 2, n 3 )= P (n 2 A x, n3A z ) = N2N3 N2-1 N3-1 Z Z m 2=0 m 3=0 I .2п .2п m 2, m 3 ) exPl j^n 2 m 2 + j^n 3 m 3 I N 2 N 3 (П.6) 0 < ni< Ni -1, i = 2,3. В соответствии с выбранным алгоритмом численного интегрирования выражения (8) сформировать массив квадратурных коэффициентов C(m 1), 0 < m 1 < N1 -1. Вычислить начальный спектр Фурье F ( 0 , k x\z) волнового поля для текущих значений глубины z = n 3 Az и волнового числа k x = m 2 Ak x F(m 1 , m 2 n 3 )= F(to, kx\z )= R( m 1 , m 2 ). Обновить значение спектрограммы .R (m 2 , n 3 ) = -~ (m 2 , n 3 ) + Ato C ( m 1)F (m 1 , m 2 Шаг 7. Цикл по частоте to. m 1 = m 1 +1, to = to + Ato. Вычислить по формулам (9) и (10) текущий фазовый сдвиг [ 2 m 1 Ato A0l mi ,m n3 )=Az^H—7—r-v 2 H v (z) m2Akx)2 Вычислить текущий спектр Фурье F (to, k x | z) волнового поля F ( m 1 , m 2 n 3 )= F ( m 1 -1, m 2 n 3 ) exp {a9 ( m 1 , m 2 n 3 )}. R( Обновить значение спектрограммы m 2 , n 3 ) = -~ (m 2 , n 3 ) + Ato C ( m 1)F ( m 1 , m 2 I n 3). Шаг 8. Критерий продолжения цикла по частоте to. Если m 1 < N1 -1, то идти к Шагу 7. Шаг 9. Критерий продолжения цикла по волновому числу k x. Если m 2 < N 2 -1, то идти к Шагу 5. Шаг 10. Критерий продолжения цикла по глубине z. Если n 3 < N 3 -1, то идти к Шагу 3. Шаг 11. С помощью обратного ДПФ спектрограммы по волновому числу k x реконструировать дискретную модель поля в вертикальном нисходящего волнового поля для дискретных значений глубины z ।-1 < m 3 Az< z । F(m2,m3 ) = B(m2,m3 zi-1)exP{jm3Akz z}; разрезе среды. p ( n 2, n 3 )= p ( n 2 A x, n 3A z ) = . масштабировать отсчеты ДПФ нисходящего волнового поля для дискретных значений глубины zi-1 < m 3 A z< zi 1 N2 -1 / =kT 2 R ( N 2 m2 = 0 m2,n3)exP j 2 п л к N 2 n2m2J, 0 < n2< N2 -1. Приложение 3. Рекурсивное миграционное преобразование Столта. Шаг 1. На ортогональном растре с интервалами дискретизации Ato и A k x вычислить по формуле (П.1) двумерное ДПФ R (m 1, m 2) радарограммы. Шаг 2. Инициализировать цикл по слоям среды. Выбрать шаг дискретизации Az глубины. Сформировать массивы Vi и zi, i = 1, 2, …, L для скоростей распространения ЭМВ и заглублений нижних границ слоев. По формуле (11) для скорости v (z ) = V 1 сформировать массив волновых чисел kz1)(m 1, m 2)= kz1)(m 1 Ato, m 2 Akx), 0<mi<Ni -1, i = 1,2. ~ Vim 3A kz ~ P ( m 2, m 3 )= U 3 2 / 32 F(m 2, m 3 ). 2J (m 2 Akx)2 +(m 3 Akz)2 Шаг 5. Рекурсия спектральных оценок в пространстве частот (Q, kx) на ортогональном растре {m 1Aw, m2Akx}: . по формуле (13) вычислить ДПФ нисходящего волнового поля для нижней границы zl текущего слоя среды F(m 1 ,m2 zz )= B(m 1 ,m2 zz-1)exp{jk^)(m,,m2)zz}; • по формуле (11) для скорости v (z )= Vl+1 распространения ЭМВ в последующем слое среды сформировать массив волновых чисел kzl+1)( m 1, m 2) 0 < mi < Ni -1, i = 1,2; . по рекурсивной формуле (14) вычислить ДПФ восходящего волнового поля для верхней границы zl последующего слоя среды B (m 1 , m2 I zz )= F(m 1 ,m2 m1 , Вычислить ДПФ восходящего волнового поля на поверхности среды l = 0, z0= 0. B ( m 1, m 2 z 0 )= R (m 1, m 2 0<mi<Ni -1, i = 1,2. Шаг 3. Цикл по слоям среды l = l+1. Шаг 4. В текущем слое z z-1 < z< z z реализовать нелинейное преобразование Столта. Для этого: . выполнить дискретизацию пространственной частоты kz с шагом Akz в интервале 0 < kz< 2 W3= 2п/ Az по формуле (П.2); . отобразить узлы ортогонального растра ( m2A kx , m3Akz) на пространство частот {to(m2,m3),m2Akx} по формуле (П.3) для скорости распространения ЭМВ v = V|; • преобразовать частоты to( m 2, m 3) к основ- ному домену 0 < Q < a по формуле (П.4); . для дискретных значений глубины zi-1 < m 3 Az< z| с помощью функции (П.5) выполнить интерполяцию отсчетов ДПФ восходящего волнового поля на нелинейном растре Шаг 6. Критерий продолжения цикла по слоям. Если l< L, то идти к Шагу 3. Шаг 7. С помощью обратного ДПФ спектра -P (m2, m3) по формуле (П.6) реконструировать дискретную модель p (n 2 , n 3) волнового поля в вертикальном разрезе среды.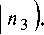
Список литературы Рекурсивное миграционное преобразование радарограммы в системе подповерхностной радиолокации
- Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов: Пер. с англ. М.: Мир. 1988. -488 с.
- Клаербоут Д.Ф. Сейсмическое изображение земных недр: Пер. с англ. М.: Недра. 1989. 407 с.
- Claerbout J.F. Basic Earth Imaging. Cambridge: Free Software Foundation. 2010. 218 p.
- Зеленков А.В., Зеленков С.А. Выбор метода миграции для обработки сигналов подповерхностной радиолокации//Электроника и электротехника. Каунас: Технология, 2004.№ 3(52). С. 41 -46.
- Klokov A., Sato M. Application of 3D-migration algorithm to GPR on an irregular ground surface//Proc. of the IGARSS, 2011. P. 870 -873.
- Yilmaz Oz., Doherty S.M. Seismic Data Analysis: processing, inversion and interpretation of seismic data. V. 1. Society of Exploration Geophysics, 2001.
- Линников О. Н., Сосулин Ю. Г., Толмазов Б. Б. Обработка сигналов и изображений в импульсном радиолокаторе подповерхностного зондирования//Радиотехника и электроника. 2004, Т. 49. № 7. С. 824 -839.
- Юфряков Б.А., Суриков Б.С., Сосулин Ю.Г., Линников О.Н. Метод интерпретации данных радиолокаторов подповерхностного зондирования//Радиотехника и электроника. 2004. Т. 49. № 12. С. 1436 -1451.
- Practical Course Introduction to Reflection Seismology -URL: http://geodus1.ta.tudelft.nl/PrivatePages/G.G.Drijkoningen/intro_seismology (дата обращения 15.04.2016).
- Лабунец Л.В. Симаков В.В. Структурный анализ сигналов в системах подповерхностной радиолокации//Электромагнитные волны и электронные системы. 2013. Т. 18. № 8, С. 49 -68.


