Релаксация остаточных напряжений в поверхностно-упрочненном призматическом образце с концентратором напряжений полукруглого профиля в условиях высокотемпературной ползучести

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2024PNRPU MECHANICS BULLETIN

Тенденция развития современного энергетического машиностроения и авиадвигателестроения предписывает разработку новых и глубокую модернизацию уже имеющихся технологий изготовления деталей газотурбинных двигателей (ГТД) с целью увеличения их ресурса.

Несмотря на многолетний опыт проектирования и эксплуатации авиадвигателей, нерешенной остается проблема сравнительно частого выхода из строя наиболее ответственных деталей ГТД по причине наличия в них технически необходимых концентраторов напряжений технологического происхождения (пазов, отверстий, канавок, выточек, резьбы и т.д.) и возникающих при эксплуатации дефектов (царапин, сколов, вмятин, порезов и т.д.). В действительности присутствие любых несплошностей негативно сказывается на прочностном ресурсе таких деталей по причине образования и последующего развития в них усталостных трещин, которые всегда имеют место при переменных циклических нагрузках. Тем не менее избежать наличия концентраторов напряжений с позиции конструирования деталей ГТД без указанных конструктивных элементов практически нельзя, а появление в деталях эксплуатационных микро- и макроповреждений зачастую обосновано попаданием в работающий агрегат посторонних предметов.

Немаловажным фактором при этом является учет отрицательного влияния на детали высоких температур, действие которых на протяжении длительной работы в процессе эксплуатации приводят к ухудшению исход- ных механических свойств материалов деталей и изменению первоначальных габаритных параметров элементов конструкций вследствие высокотемпературной ползучести и коробления.

Отметим, что подавляющее число случаев разрушения эксплуатируемых деталей, например ГТД, сводятся к развитию различного рода приповерхностных концентраторов напряжений в условиях действия нагрузок. Сопутствующим фактором при этом считается появление в работающих деталях значительных по величине эксплуатационных растягивающих напряжений, которые могут накапливаться в процессе нагружения. Частичное снижение их интенсивности возможно, например, в случае предварительной обработки деталей методами поверхностного пластического деформирования (ППД), в результате чего в приповерхностных слоях материала формируются компенсирующие сжимающие остаточные напряжения (ОН). Эффективность применения методов ППД подтверждается необозримым количеством научных работ, демонстрирующих повышение показателей статической и усталостной прочности, твердости, шероховатости, износостойкости и прочих характеристик, среди которых можно выделить «ранние», основополагающие работы [1–12], а также не менее значимые работы по упрочнению гладких «бездефектных» деталей [13–16] и деталей с концентраторами напряжений [2; 3; 9; 10; 14; 17–27].

Особый научно-практический интерес представляют вопросы влияния поверхностного упрочнения деталей авиадвигателестроения на сопротивляемость реоло- гическим процессам при высокотемпературной ползучести. Это вызвано тем, что длительное действие повышенных температур в энергосиловых установках приводит к перераспределению и релаксации напряжений в материале комплектующих изделий ГТД и, как следствие, к ухудшению качества поверхностного слоя. Следовательно, возникает необходимость в анализе напряженно-деформированного состояния (НДС) как упрочненных, так и неупрочненных деталей работающих в условиях температурно-силового воздействия. В подтверждение этому в исследовательских работах [4; 7; 13; 16; 30; 33] затрагивается проблема снижения прочности гладких деталей авиадвигателестроения и энергомашиностроения по причине релаксации сжимающих ОН, предварительно наведенных упрочнением. Наиболее сложно ситуация обстоит в отношении упрочненных тел с концентраторами напряжений, о чем свидетельствуют, например, работы [30; 34], в связи с чем настоящее исследование посвящено оценке релаксации ОН в предварительно упрочненном призматическом образце с надрезом полукруглого профиля.

Постановка задачи

В настоящей работе рассматривается призматический образец размерами 100×10×10 мм, изготовленный из широко используемого в авиадвигателестроении жаропрочного сплава ЭП742, верхняя грань которого подвержена виброударному ультразвуковому поверхностно-пластическому упрочнению дробью (УЗУ), а затем на нее нанесен сквозной надрез полукруглого профиля радиусом ρ = {0,1; 0,2; 0,3; 0,5} мм (рис. 1). Задача сведена к оценке кинетики предварительно наведенных поверхностным упрочнением ОН образца, который находится в условиях температурной выдержки без нагрузки (термоэкспозиции) при температуре 650°C в течение 300 ч. Вводится декартова система координат так, чтобы плоскость x 0 z совмещалась с упрочненной гранью, а ось 0 y была направлена по глубине упрочненного слоя (см. рис. 1).

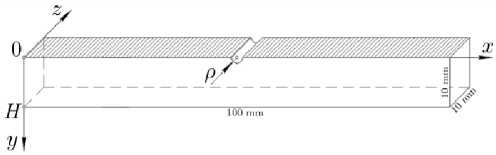
Рис. 1. Схематическое изображение поверхностно-упрочненного призматического образца с надрезом полукруглой формы

• Fig. 1.    Schematic representation of a surface-hardened prismatic specimen with a notch of a semicircle profile

Исходной информацией для выполнения расчета полей ОН и пластических деформаций (ПД) являются экспериментальные данные распределения компоненты ° x = ° x (У) Для гладкого «бездефектного» призматиче- ского образца, полученные после виброударного ультразвукового упрочнения дробью (рис. 2) [16].

Метод решения задачи о релаксации ОН в призматическом образце в условиях ползучести состоит из нижеследующих этапов.

• 1.    Реконструкция (восстановление) полей ОН в гладком бездефектном образце после процедуры поверхностного пластического упрочнения по известной экспериментальной информации.

• 2.    Решение задачи о перераспределении ОН после нанесения полукруглого надреза на верхнюю упрочненную поверхность.

• 3.    Решение задачи о релаксации сформировавшихся ОН в призматическом образце с надрезом после опережающего поверхностно-пластического упрочнения (ОППД) в условиях высокотемпературной ползучести материала при длительной термоэкспозиции.

Именно в такой последовательности излагается материал настоящей статьи.

Метод реконструкции полей остаточных напряжений и пластических деформаций поверхностно-упрочненного призматического образца с полукруглым надрезом по известной экспериментальной информации

Рассмотрим сначала метод реконструкции полей ОН и ПД для гладкого «бездефектного» образца по известной экспериментальной информации, подробно описанный в работе [35]. Призматический образец подвергается процедуре поверхностного пластического деформирования (ППД) по верхней грани, после чего образуется тонкий упрочненный слой толщиной 100÷300 мкм. В соответствии с [35] установлено, что компоненты тензоров ОН и ПД зависят только от координаты у, т.е. ° x = ° x ⁽ у ), ° z = ° z ⁽ у ), ° у = ° у ⁽ у ) = 0 и все недиагональные компоненты ОН и ПД полагаются равными нулю в силу их малости. Ненулевыми компонентами остаточных деформаций являются упругие e i = e i ( у ), пластические q i = q i ( у ) и полные s i = s i ( у ) ( i = x , у , z ) соответственно. Согласно введенной гипотезе плоских сечений для компонент остаточных полных деформаций выполняется кинематическое условие:

^s x ⁽ у ) = ^s z ⁽ у ) = °.                     ⁽¹⁾

Для рассматриваемого случая изотропного поверхностного упрочнения (выполняется условие q x ( у ) = q_z ( у )) с учетом условия пластической несжимаемости q_x + q_y + q_z = 0 расчетные формулы для ОН и ПД принимают вид [35]:

1 — v

° z ⁽ у ) = ° x ⁽ у ), Q x ⁽ у ) = Q z ⁽ у ) = — ° x ⁽ у ),

^E (2)

( л 2(1 - v) qy(у) = ——° x(у), E где v – коэффициент Пуассона, E – модуль Юнга.

В соответствии с (2) все компоненты тензоров ОН и ПД выражаются через компоненту ax (у), поэтому для реконструкции НДС упрочненного образца достаточно иметь известную экспериментальную зависимость ax = ax (у) в пределах упрочненного слоя (для рассматриваемого образца из сплава ЭП742 – точки на рис. 2), после чего необходимо построить аппроксимацию этой зависимости и экстраполировать ее на все значения 0 < у < H (где H = 10 мм - высота призматического образца). Согласно [35] для реализации описанной методики предложена зависимость вида ax (У) = ao -ai exP

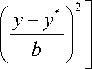
где a ₀, a 1 , b , у - параметры аппроксимации экспериментальной эпюры a _x ( у ), методика определения которых подробно изложена в [35], согласно которой они имеют значения: a ₀ = 13,38 МПа; a 1 = 1101 МПа; b = 0,093 мм; у = 0,034 мм. На рис. 2 сплошной линией показана зависимость a _x = a _x ( у ) с использованием аппроксимации (3).

Таким образом, при известной зависимости (3) остальные компоненты ОН и ПД в соответствии с (2) будут иметь аналитическое представление.

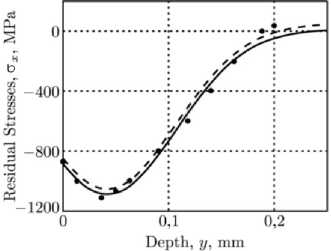
Рис. 2. Данные для компоненты a _x = a _x ( у ) после упрочнения УЗУ поверхности призматического образца из сплава ЭП742: экспериментальные (точки), расчетные (сплошная линия) по аппроксимации (3) и расчетные (штриховая линия) для термоупругой задачи

• Fig. 2.    Data for the component a _x = a _x ( у ) after ultrasonic surface strengthening of the prismatic specimen made of EP742 alloy: experimental (points), calculated (solid line) by approximation (3), and calculated (dashed line) for the thermoelastic problem

На втором этапе компоненты тензора остаточных ПД qi = qi (у) (i = x, у, z), которые определяются из соотношений (2), моделируются фиктивными температурными деформациями с использованием зависимостей qi( у) = в,(Т (у ))[T (у) — To], i = x, у, z,  0 < у < H,

где P i ( T ( у )) - коэффициенты температурного расширения, T = T ( у ) - неоднородное температурное поле с малым градиентом температур, распределение которого можно выбирать произвольно: T ₀ = T ( H ) = 20 °C -фиксированное значение температуры на грани образца при у = H (см. рис. 1), T * = T (0) = 30 °C - значение температуры на противоположной (упрочненной) грани при у = 0 . При значениях q i ( у ), известных из (2) и (3), и заданном распределении T = T ( у ) по формуле (4) вычисляются коэффициенты температурного расширения P i = в i ( T ( у )), необходимые для дальнейших расчетов.

На следующем этапе в соответствии с технологией ОППД на предварительно упрочненный гладкий образец наносится сквозной надрез полукруглого профиля за счет удаления части материала при сохранении температурного поля, полученного для гладкого образца в объеме образца без учета надреза. Другими словами, в объеме образца без надреза сохраняются рассчитанные пластические деформации для гладкого образца.

На заключительном этапе по известным из расчета значениям в i = в i ( T ( у )) с использованием метода конечных элементов (МКЭ), реализованным в программной среде ANSYS Mechanical APDL, численно решается задача термоупругости, в результате чего становится известным распределение ОН в образце с концентратором напряжений полукруглого профиля. Для частичной экспериментальной проверки разработанного метода сведения исходной задачи к задаче фиктивной термоупругости МКЭ решалась задача и для гладкого (бездефектного) образца. На рис. 2 штриховой линией показана зависимость для a _x = a _x ( у ), полученная МКЭ, при этом наблюдается хорошая согласованность этой зависимости с экспериментальными данными и с аппроксимацией (3).

Численный метод расчета кинетики остаточных напряжений в поверхностно-упрочненном призматическом гладком образце и образце с надрезом полукруглого профиля в условиях ползучести

Рассматривается задача расчета кинетики наведенных после упрочнения ОН в призматическом образце 100×10×10 мм из сплава ЭП742 с полукруглым надрезом в условиях высокотемпературной ползучести при отсутствии внешних силовых нагрузок. Согласно [16] процесс релаксации ОН с температурной выдержкой без силового нагружения и известном НДС после упрочнения будем называть термоэкспозицией. Предполагается мгновенное прогревание образца с температуры Т0 = 20 °C до температуры T = 650 °C с последующей температурной выдержкой по времени t = 300 ч. Для сплава ЭП742 E0 = 2,21-105 МПа - мо- дуль Юнга при температуре T0, E1 = 1,79 -105 МПа -модуль Юнга при температуре T1 . Предполагается, что коэффициент Пуассона v = 0,3 и не зависит от температуры.

После процедуры упрочнения в момент времени t = 0 - 0 при температуре T 0 = 20 °C имеем распределение ОН и ПД, задаваемое (2) и (3):

° z ( у ) = ° x ⁽ у ), q x ⁽ у ) = q z ⁽ у ) = ^- 1^v ° x ⁽ у ),

E qy( у ) =

2(1— v ) г 1

—--° x ⁽ У )•

E ₀

При мгновенном прогреве упрочненного образца с температуры T 0 до температуры T ( T >  T 0 ) в предположении, что новых пластических деформаций не возникает, получаем распределение полей ОН и ПД для момента времени t = 0 + 0 :

°x(у) = - rE- qx(у), °z(у) = °x(у), (6) 1 - v где компонента ПД qx(y) вычисляется в соответствии с формулой (5). Сравнивая (5) и (6), можно сделать вывод, что напряжение °x (у) при температуре T можно получить, умножив функцию °x (у) при температуре упрочнения T0 на коэффициент E0/ E1. Таким образом, в момент изменения от температуры T0 до температуры T1 произойдет ступенчатое изменение напряжений °x (у) и °z (у) вследствие изменения модуля Юнга и неизменности qx (y).

Рассмотрим решение задачи о релаксации остаточных напряжений в образце с надрезом в условиях ползучести. Кроме уже использованных выше упругих характеристик, необходимо иметь реологическую модель для сплава ЭП742 при температуре 650°С. В настоящей работе использована теория установившейся ползучести р =3СS"-11с. -15. с.. I, (7) pi 2 I i 3 ’’I ’ где pj - компоненты скорости деформации ползучести, S - интенсивность напряжений, ° - компоненты тензора напряжений, Sj - символ Кронекера, c, n - константы материала [11; 16].

Поставленная задача решалась численно методом конечных элементов в программной среде ANSYS Mechanical APDL, поэтому из библиотеки выбрана степенная модель ползучести Нортона, которая в одноосном случае представлена зависимостью еcr = С1°C2e-C3/T , (8)

где C ₁ , C ₂ , C ₃ – константы материала, T – значение абсолютной температуры, е _cr - скорость деформации ползучести, при этом в нижеследующих расчетах для согласования обозначений (7) и (8) полагалось, что C 3 = 0, C ₂ = n , C 1 = c .

Подробное изложение численного метода конечноэлементного моделирования НДС призматического образца с надрезом с точки зрения построения геометрической дискретной модели изложено в [21]. Поэтому кратко изложим особенности процедуры настройки блока решателя программы для учета деформации ползучести в среде ANSYS Mechanical APDL.

Согласно настоящей методике, дискретизация по времени t при использовании программного комплекса ANSYS осуществляется заданием временного шага A t в разделе настроек решателя, где от 1 ₀ = 0 до t 1 = 1 ч временной шаг интегрирования соответствует A t j = 0,02 ч, после чего от t 1 = 1 ч и до окончания времени t _к температурной выдержки - A t _к = 1 ч. Это связано с тем, что в пределах первого часа температурного нагружения скорость релаксации ОН имеет наибольшую величину, поэтому шаг интегрирования в области, прилегающей к t = 0, должен быть малым.

Отметим, что с помощью МКЭ решалась задача и для гладкого (без надреза) образца в условиях ползучести с целью проверки адекватности предложенного метода данным расчета методом сеток и экспериментальным данным для гладкого образца, представленных в [16], поскольку решение для образца с надрезом по мере удаления от него (по координате x , см. рис. 1) должно приближаться к решению для гладкого образца.

Результаты расчетов и их анализ

Численное исследование кинетики ОН при ползучести в поверхностно-упрочненном призматическом образце из сплава ЭП742 с надрезом полукруглого профиля радиуса ρ = {0,1; 0,2; 0,3; 0,5} мм в условиях термоэкспозиции при температуре 650°C. Приведем результаты расчетов для гладкого образца, представленные на рис. 3. Здесь приведена кинетика ОН для компоненты ° _x = ° _x ( y , t ) с учетом их релаксации при высокотемпературной ползучести в гладком поверхностно упрочненном образце по глубине h от упрочненной поверхности в зависимости от времени выдержки. Кривой 1 показаны расчетные (сплошная линия) по аппроксимации (2) и расчетные (штриховая линия) по МКЭ результаты начального НДС при температуре T 0 = 20 °C в момент времени t = 0 . Аналогичные данные для случая «мгновенно» прогретого до температуры T = 650 °C образца показаны кривой 2 . Кривым 3 и 4 соответствуют расчетные по МКЭ (кривая 3 ) и расчетные по методу сеток (кривая 4 ) [16] зависимости ОН

° x = ¹⁵ x ( У , t ) при термоэкспозиции длительностью t _к = 100 ч Кривые 5, 6 соответствуют распределению ОН после температурной разгрузки с T = 650 °C до Т ₀ = 20 °C в момент времени t _к = 100 ч для экспериментальных значений (кривая 5 , точки) [16], для расчетных данных по методу сеток (штриховая кривая 5 ) [16], для расчетных данных по МКЭ (кривая 6 ).

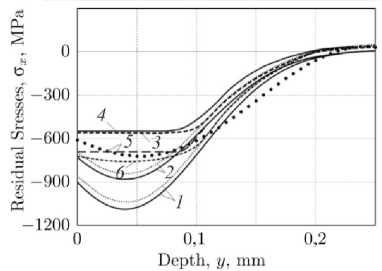
Рис. 3. Распределение ОН для компоненты ° x = ° x ( y , t ) в гладком образце из сплава ЭП742 при ползучести в зависимости от времени выдержки t : 1 - результаты расчета по аппроксимации (3) (сплошная линия) и по МКЭ (штриховая линия) при температуре 20°C ( t = 0); 2 -результаты расчета с использованием аппроксимации (3) (сплошная линия) и по МКЭ (штриховая линия) при температуре 650°C( t = 0); 3 - расчетные данные по МКЭ ( t = 100 ч); 4 - расчетные данные по методу сеток [16] ( t = 100 ч); 5 - данные после температурной разгрузки (эксперимент - точки, метод сеток - штриховая линия, t = 100 ч); 6 - расчетные данные по МКЭ после температурной разгрузки ( t = 100 ч)

Fig. 3. Distribution of residual stresses for the component ° x = ° x ( У, t ) in a smooth specimen made of EP742 alloy under creep depending on holding time t : 1 - calculation results by approximation (3) (solid line) and by FEM (dashed line) at a temperature of 20°C ( t = 0); 2 - calculation results by approximation (3) (solid line) and by FEM (dashed line) at a temperature of 650°C ( t = 0); 3 - calculation results by FEM ( t = 100 hrs); 4 - calculated data by the grid method [16] ( t = 100 hrs); 5 - data after thermal unloading (experiment -points, grid method - dashed line, t = 100 hrs); 6 - calculated data by FEM after thermal unloading ( t = 100 hrs)

Анализ погрешности кинетики ОН по компоненте ° x = ° x ( y , t ) между экспериментальными и расчетными данными работы [16] и полученными по МКЭ численными результатами проводился в пределах толщины упрочненного слоя гладкого «бездефектного» образца по норме:

Л ° =

■ 100%,

четной величины; ° р’ ( y k ) - компоненты тензора ОН второй расчетной величины или экспериментальные данные; n – количество точек дискретизации указанного отрезка.

Из сравнительного анализа следует, что за 100 ч термоэкспозиции расхождение между результатами расчета ОН, полученными по методу сеток ( ° р '( y k )) [16], и результатами численного расчета по МКЭ ( ° р² ( y k )) по норме (9) составило Л ° = 7,87 % . При аналогичном сопоставлении расчетных результатов ОН для случая температурной разгрузки упрочненного образца в момент времени t = 100 ч, полученных по методу сеток и по данным эксперимента, с результатами численного расчета на основе МКЭ расхождения составили Л ° = 10,39% и Л ° = 12,85% соответственно. Таким образом, можно констатировать хорошее для условий ползучести соответствие результатов расчета по разным методам экспериментальным данным. Это заключение не противоречит замечанию Ю.Н. Работнова: «… разница в 20 % по деформациям между кривыми ползучести, снятыми при одном и том же напряжении для данной температуры на образцах из материала (даже) одной плавки, не считается чрезмерно большой» [36].

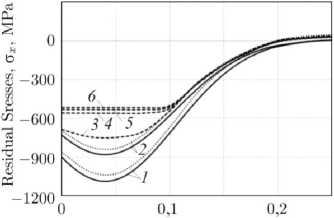
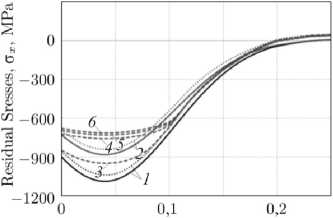
Детализированное представление кинетики ОН для компоненты ° x = ° x ( y , t ) в пределах толщины упрочненного слоя для гладкого образца при высокотемпературной ползучести за разное время термоэкспозиции t показано на рис. 4. Здесь, как и на рис. 3, кривыми 1 и 2 представлены расчетные по аппроксимации (3) (сплошные линии) и расчетные по МКЭ (штриховые линии) эпюры распределения ОН, полученные после упрочнения образца до наступления установившейся стадии ползучести ( t = 0) в «холодном» состоянии (при Т ₀ = 20 °C) и при моментальном прогреве образца до T = 650 °C соответственно. Кривые 3 - 6 описывают кинетику расчетных значений ОН ° x = ° x ( y , t ) по МКЭ при термоэкспозиции (см. рис. 4, а , T = 650 °C) и при температурной разгрузке упрочненного образца (см. рис. 4, b , T 0 = 20 °C) за время выдержки t (кривая 3 - t = 1 ч, кривая 4 – t = 100 ч, кривая 5 – t = 200 ч, кривая 6 – t = 300 ч).

На основе формулы (9), приняв расчетную величину °,Р‘(yk) = °x (yk ,0) при T0 = 20 °C, а величину ° р’( yk) = ° x (yk, t) в моменты времени t = {1; 100; 200; 300} ч, T = 650 °C, выполнялась оценка интенсивности релаксации ОН в зависимости от времени выдержки t с последующей температурной разгрузкой. Наибольший интерес с прикладной точки зрения представляют эпюры напряжений после ползучести и температурной разгрузки, представленные на рис. 4, b. Фактически здесь показано, как условия эксплуатации в режиме термоэкспозиции при T1 = 650 °C с различными временами выдержки и последующей температурной разгрузкой до T0 = 20 °C сказываются на релаксации остаточных напряжений. Сравнивая графики на рис. 4, b, с маркерами 3, 4, 5 и 6 с исходным графиком после упрочнения (маркер 1), с использованием формулы (9), получено, что за время t = 1 ч интегральная оценка уменьшения (по модулю) величины остаточных напряжений составила 6,2 %, за t = 100 ч – 26,42 %, за t = 200 ч – 30,66 %, за t = 300 ч – 33,22 %.

Дальнейшее изучение кинетики ОН в условиях термоэкспозиции осуществлялось для поверхностно упрочненного призматического образца с полукруглым надрезом радиуса ρ = {0,1; 0,2; 0,3; 0,5} мм. На рис. 5 показаны графики кинетики расчетных по МКЭ значений ОН по компоненте ст x = ст x ( h , t ) для случаев упрочненного гладкого образца (кривые 1 ) и образца с надрезами радиуса ρ = 0,2 мм (кривые 2 ), ρ = 0,3 мм (кривые 3 ) и ρ = 0,5 мм (кривые 4 ) при t = 0, t = 1 ч, t = 50 ч и t = 300 ч.

Depth, т/, mm

Depth, у, mm

a

b

Рис. 4. Кинетика компоненты ст x =ст x ( y , t ) при ползучести для гладкого образца в зависимости от времени выдержки t при термоэкспозиции ( a ) и при температурной разгрузке ( b ): 1 – расчетная эпюра по МКЭ (штриховая линия) и расчетная эпюра по аппроксимации (3) (сплошная линия) при температуре 20°C ( t = 0); 2 - расчетная эпюра по МКЭ (штриховая линия) и расчетная эпюра с использованием аппроксимации (3) (сплошная линия) при температуре 650°C ( t = 0); 3 – t = 1 ч, 4 – t = 100 ч, 5 – t = 200 ч, 6 – t = 300 ч

Fig. 4. Kinetics of the component ст x = CT x ( y, t ) under creep for a smooth specimen, depending on the holding time t during thermal exposure ( a ) and during thermal unloading ( b ): 1 – FEM calculated curve (dashed line) and curve by approximation (3) (solid line) at a temperature of 20°C ( t = 0); 2 – FEM calculated curve (dashed line) and curve by approximation (3) (solid line) at a temperature of 650°C ( t = 0); 3 – t = 1 hr, 4 – t = 100 hrs, 5 – t = 200 hrs, 6 – t = 300 hrs

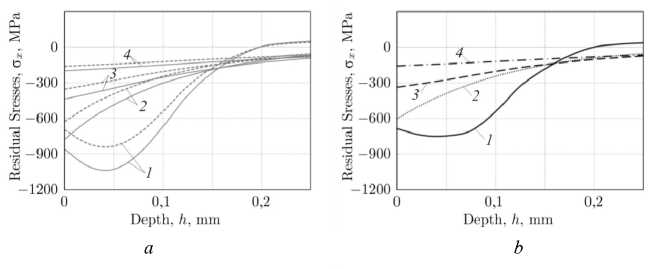
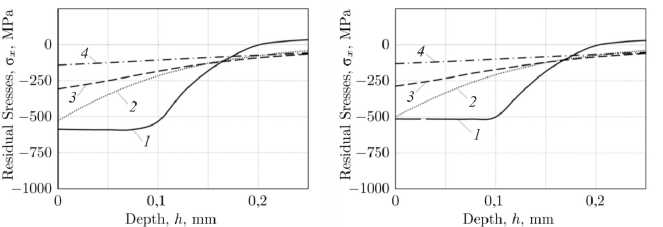
Рис. 5. Кинетика компоненты ст x = ст x ( h , t ) при термоэкспозиции для упрочненных гладкого образца и образца с надрезом р в различные моменты времени t : а – t = 0; b – t = 1 ч; c – t = 50 ч; d – t = 300 ч: 1 - решение для гладкого образца; 2 - решение при ρ = 0,2 мм; 3 - решение при ρ = 0,3 мм; 4 - решение при ρ = 0,5 мм

c

d

Fig. 5. Kinetics of the component ст x = ст x ( h , t ) during thermal exposure for hardened smooth specimen and specimen with a notch р at different moments in time t : а – t = 0; b – t = 1 hr; c – t = 50 hrs; d – t = 300 hrs: 1 - solution for the smooth specimen; 2 - solution for ρ = 0,2 mm; 3 - solution for ρ = 0,3 mm; 4 - solution for ρ = 0,5 mm

a

b

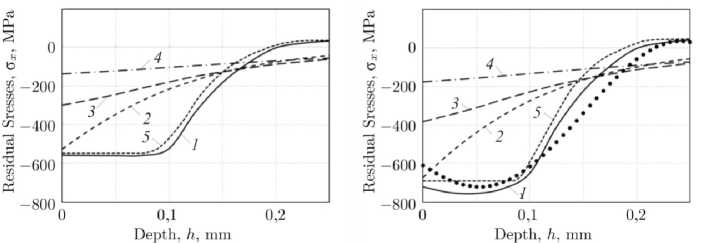
Рис. 6. Распределение компоненты σ x =σ x ( h , t ) при ползучести в момент времени t = 100 ч при термоэкспозиции ( а ) и при температурной разгрузке ( b ): 1 - решение для гладкого образца; 2 – решение при ρ = 0,2 мм; 3 – решение при ρ = 0,3 мм; 4 – решение при ρ = 0,5 мм; 5 - решение для гладкого образца методом сеток; точки – экспериментальные данные для гладкого образца

Fig. 6. Distribution of the component σ x =σ x ( h , t ) during creep at time t = 100 hrs during thermal exposure ( a ) and during thermal unloading ( b ): 1 - solution for the smooth specimen; 2 - solution for ρ = 0,2 mm; 3 - solution for ρ = 0,3 mm; 4 - solution for ρ = 0,5 mm;

5 - solution for the smooth specimen by the grid method; points - experimental data for the smooth specimen

При этом распределение компоненты ОН σ x =σ x ( h , t ) на рис. 5, a, соответствует состоянию упрочненных образцов в момент времени t = 0 при температуре T ₀ = 20 °C (сплошные линии) и мгновенного изменения температуры до T ₁ = 650 °C (пунктирные линии). Для единообразия трактовки расчетных данных на рис. 5 и в дальнейшем изложении материала статьи для образцов с надрезами h – это глубина по упрочненному слою от дна надреза, т.е. h = y -ρ ( y ≥ρ ), а для гладкого образца – h = y .

Анализ полученных графиков на рис. 5 показывает, что наибольшая интенсивность релаксации сжимающих ОН для компоненты σ x =σ x ( h , t ) при высокотемпературной ползучести наблюдается для поверхностно упрочненного образца с полукруглым надрезом ρ = 0,2 мм (кривая 2 ). При этом за время t = 1 ч температурной выдержки (см. рис. 5, а ) в соответствии с нормой (9) интегральный уровень ОН снижается (по модулю) на 62,82 % по отношению к начальному «холодному» состоянию образца после упрочнения ( t = 0, T ₀ = 20 °C). Для расчетных случаев упрочненных образцов с ρ = 0,3 мм и ρ = 0,5 мм снижение величины σ x =σ x ( h , t ) за t = 1 ч составляет 27,32 и 27,34 % соответственно.

На рис. 6 представлены графики для всех рассматриваемых расчетных случаев упрочненного гладкого образца и образца с надрезом ρ при термоэкспозиции (см. рис. 6, а) и температурной разгрузке (см. рис. 6, b) за время выдержки t = 100 ч для компоненты ОН σx=σx(h,t) по глубине h от дна концентратора. Кривой 1 представлены результаты распределения ОН для гладкого образца, кривыми 2-4 – результаты расчета для образцов с надрезами ρ = {0,2; 0,3; 0,5} мм соответственно. Для сравнения на графиках кривой 5 отображены результаты расчетов кинетики ОН, полученные методом сеток для гладкого упрочненного образца, а точками на рис. 6, b, представлены экспериментальные данные σx=σx(h,t) для этого же образца в момент температурной разгрузки при t = 100 ч.

Многочисленные результаты расчета, частично представленные на рис. 4–6, и их анализ позволяют сделать определенные выводы. Во-первых, с увеличением радиуса надреза ρ интенсивность релаксации ОН по компоненте σ x =σ x ( h , t ) за равное время выдержки t при температуре T ₁ = 650 °C существенно снижается. Во-вторых, сравнение данных для σ x =σ x ( h , t ) после температурной разгрузки свидетельствует, что после «эксплуатации» образца в условиях термоэкспозиции сохраняется еще значительный уровень остаточных напряжений (см. рис. 5 и 6), причем с увеличением времени выдержки интенсивность релаксации резко падает, что связано с резким падением скорости ползучести для получаемых ОН. Например, для всех вариантов образцов с надрезами и гладких образцов сравнение величин σ x =σ x ( h , t ) при разгрузке для t = 100 ч и t = 300 ч дает отличие в 4–7 % в соответствии с (9).

Не менее значимый интерес при исследовании кинетики ОН в поверхностно-упрочненном призматическом образце с полукруглым надрезом ρ представляет компонента касательных напряжений σ xy =σ xy ( h , t ). Оценка численных значений этой компоненты ОН осуществлялась по глубине h = y - V3 ρ /2 от поверхности концентратора напряжений с радиусом ρ в сечении, удаленном в продольном направлении от центрального поперечного сечения (проходящего через дно концентратора напряжений) на расстояние ρ/2. Как отмечалось ранее в работе [16], учет недиагональных компонент ОН необходим при проведении прочностных расчетов для поверхностно-упрочненных тел призматической формы с мелкими надрезами.

a

b

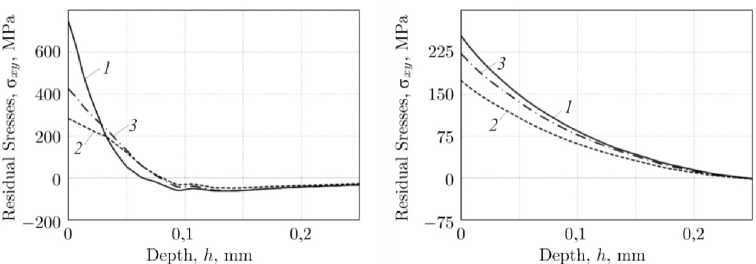
Рис. 7. Релаксация компоненты ст xy = СТ xy ( h , t ) при термоэкспозиции при р = 0,1 мм ( а ) и р = 0,3 мм ( b ) в различные моменты времени t : 1 – решение для t = 0; 2 - решение для t = 100 ч; 3 - решение после температурной разгрузки при t = 100 ч

Fig. 7. Relaxation of the component ст xy = СТ xy ( h , t ) during thermal exposure with р = 0.1 mm ( a ) and р = 0,3 mm ( b ) at various time points t : 1 – solution for t = 0; 2 – solution for t = 100 hrs; 3 – solution after thermal unloading at t = 100 hrs

В этой связи для расчетных случаев образца с надрезом радиусом ρ = 0,1 мм (рис. 7, а ) и ρ = 0,3 мм (рис. 7, b ) представлена кинетика ОН по компоненте ст xy =ст xy ( h , t ) в моменты времени t = {0; 1; 50; 100} ч для термоэкспозиции и температурной разгрузки. Как видно из представленных данных, релаксация касательных ОН наиболее эффективно проявляется в случае упрочненного образца с надрезом ρ = 0,1 мм: с момента начального НДС при t = 0, T 0 = 20 °C за 100 ч термоэкспозиции при температуре T = 650 °C составляет по норме (9) для случая термоэкспозиции 100,21 %, а для случая температурной разгрузки – 52 %.

Заключительный анализ настоящего исследования состоял в оценке зависимости величины прогиба упрочненного образца от времени термоэкспозиции t в условиях ползучести по длине образца (0 <  x <  100 мм). На рис. 8 представлены результаты расчета прогибов упрочненных гладкого образца (сплошная линия) и образцов с надрезами ρ = 0,1 мм (штриховая линия) и ρ = 0,3 мм (штрихпунктирная линия) в начальный момент времени t = 0 при температуре T ₀ = 20 °C (кривые 1) и в момент времени t = 300 ч при температуре T = 650 °C (кривые 2 ). Оценка прогибов осуществлялась в срединной горизонтальной плоскости ( y = 5 мм). По наибольшим прогибам в центральном поперечном сечении ( x = 50 мм) установлено, что прогибы f для рассматриваемых случаев за время t = 300 ч температурной выдержки уменьшаются в среднем на 22 %.

Таким образом, надрезы и вызванные ими ОН существенно не сказываются на геометрических характеристиках упрочненных образцов, по сравнению с упрочненными гладкими образцами. В процессе ползучести происходит частичное восстановление геометрии упрочненных образцов (уменьшение величины прогиба), имевших до упрочнения призматическую форму.

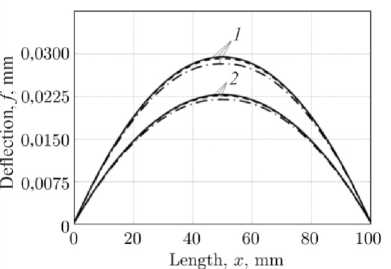
Рис. 8. Прогибы образца f в срединной плоскости ( y = 5 мм) при термоэкспозиции в начальный момент времени t = 0 при температуре 20°C (кривые 1 ) и в момент времени при t = 300 ч при температуре 650°C (кривые 2 ): упрочненный гладкий образец - сплошная линия; упрочненный образец с надрезом ρ = 0,1 мм - пунктирная линия; упрочненный образец с надрезом ρ = 0,3 мм - штрихпунктирная линия

Fig. 8. Sample deflections f in the midplane ( y = 5 mm) during thermal exposure at the initial time t = 0 at a temperature of 20°C (curves 1 ) and at time t = 300 hrs at a temperature of 650°C (curves 2 ): hardened smooth specimen - solid line; hardened specimen with a notch ρ = 0.1 mm - dashed line; hardened specimen with a notch ρ = 0,3 mm - dash-dotted line

Заключение

• 1.    Разработан численный метод расчета кинетики остаточных напряжений в поверхностно-упрочненном призматическом образце со сквозным одиночным надрезом полукруглого профиля в условиях ползучести при термоэкспозиции, основанный на известном напряженно-деформированном состоянии для гладкого образца и технологии опережающего поверхностно пластического деформирования.

• 2.    Выполнена проверка адекватности результатов расчета кинетики остаточных напряжений при ползучести по разработанному методу экспериментальным

• 3.    Показано, что происходит существенная релаксация остаточных напряжений для всех исследованных образцов с надрезами ρ = {0.1; 0.2; 0.3; 0.5} мм, но после процесса термоэкспозиции они имеют еще значительную величину в области сжатия материала, прилегающей к надрезу, при этом происходит падение скорости релаксации остаточных напряжений практически до полной остановки релаксационного эффекта при больших временах выдержки образцов при температуре 650°C вследствие резкого падения скорости ползучести с уменьшением уровня (по модулю) остаточных напряжений.

данным и данным расчета по методу сеток в частном случае гладкого упрочненного образца, которые являются асимптотическими данными для образца с надрезом вдали от концентратора.