Релейная автономная система управления группировкой спутников, базирующейся на низкой околоземной орбите
Автор: Богданов Кирилл Андреевич, Тимаков Сергей Николаевич, Зыков Александр Владимирович, Субботин Алексей Владимирович
Журнал: Космическая техника и технологии @ktt-energia
Рубрика: Динамика, баллистика, управление движением летательных аппаратов
Статья в выпуске: 1 (28), 2020 года.
Бесплатный доступ
Предложен релейный алгоритм управления группировкой космических аппаратов (КА), в состав которой входят «пассивный» (виртуальный) КА, движущийся по невозмущенной круговой орбите, и несколько «активных», маневрирующих относительно него, КА. Задача управления состоит в удержании каждого активного КА на своей финитной траектории относительно виртуального аппарата, задающего центр группировки, с минимально возможным расходом топлива. Для описания движения маневрирующих спутников относительно центра группировки используются модифицированные уравнения Хилла-Клохесси-Уилтшира, учитывающие сжатие Земли и аэродинамическое сопротивление. Основное внимание в работе уделено исследованию существования устойчивых предельных циклов и нахождению областей их притяжения, а также поиску значений параметров релейной системы управления, обеспечивающих минимальный расход топлива на поддержание надлежащего динамического поведения группировки.
Релейное управление, метод точечных преобразований, управление формациями, предельный цикл, фазовая плоскость
Короткий адрес: https://sciup.org/143177924
IDR: 143177924 | УДК: 629.783.015.076.6:681.5.01 | DOI: 10.33950/spacetech-2308-7625-2020-1-98-110
Текст научной статьи Релейная автономная система управления группировкой спутников, базирующейся на низкой околоземной орбите
Автономное управление групповым полетом спутников находится в центре внимания специалистов в области управления движением и навигации, о чем свидетельствует огромный, неослабевающий поток научно-исследовательских работ по этой тематике, что связано с широкими возможностями использования группировки спутников в решении прикладных и научных задач. Это, прежде всего, создание когерентных радиолокаторов с синтезированной апертурой для исследования Земли и дальнего космоса, системы навигации с элементами космического базирования GPS , ГЛОНАСС, системы глобальной космической связи, создание системы распределенных сенсоров для наблюдения метеорологической обстановки в режиме реального времени. Далеко не полный перечень задач, решаемых космической группировкой спутников, можно найти в работе [1].
Динамическое поведение группировки спутников на орбитах, близких к круговым, описывается дифференциальными уравнениями как в оскулирующих параметрах орбиты [2], так и в декартовых координатах относительно орбитальной системы координат long vertical long horizontal или системы координат Хилла (Hill) [2, 3], привязанной к главному (пассивному) аппарату. В работах [4–6] показано, что аналитические решения линеаризованных уравнений относительного движения при использовании этих двух методов описания полностью эквивалентны. При описании динамики низкоорбитальных группировок на продолжительном временном интервале учитываются эффект сжатия Земли (дипольный член разложения J2 гравитационного геопотенциала) и атмосферное сопротивление [7]. Существенный вклад в модификацию классических уравнений Хилла–Клохесси–Уилтшира (HCW) [2, 3] был сделан в работах [8, 9] и верифицирован в статье [10]. Данная модификация учитывает поправку орбитального периода и дрейф долготы восходящего узла из-за J2-возмущения, и в то же время сохраняет структуру уравнений HCW неизменной, что позволяет достаточно просто находить их аналитическое решение.
Другим источником возмущения низкоорбитальной Кеплеровой орбиты спутников является атмосферное сопротивление. В работе [11] было показано, как, варьируя разницу в аэродинамическом сопротивлении между двумя спутниками, управлять относительным движением группировки. Однако, коррекция орбитального движения спутников вокруг Земли требует расхода топлива. В связи с этим возникает задача минимизации расхода топлива на удержание группировки спутников вблизи заданной круговой орбиты. В данной работе эта задача решается одновременно с задачей удержания параметров относительного движения каждого спутника из группировки в заданном диапазоне.
Многие авторы при синтезе управления группировкой спутников используют метод LQR [12] или метод функций Ляпунова [13]. Однако, если в качестве исполнительных органов применяются электрореактивные двигатели, тяга которых не изменяется, корректировать орбиту маневрирующих спутников с помощью этих методов можно, как правило, через равные промежутки времени или в определенных точках (фазах) траектории относительного движения, варьируя время работы двигательной установки. При этом к моменту выдачи очередного корректирующего импульса параметры траектории могут превысить их лимитирующие значения, что может приводить к излишним затратам топлива на поддержание требуемой конфигурации группового полета спутников. В данной работе методами теории управления (без привлечения методов проектной баллистики) синтезирован релейный закон управления, создающий управляющее воздействие в режиме реального времени по закону обратной связи. Обратная связь формируется автономно в бортовом компьютере каждого маневрирующего спутника, принадлежащего x – 2ωc y. – ω2
c 2 + 2 +
6 J 2 R e 2 R 2
(1 – 3sin2 i sin2 θ ) x
группировке, по информации с измерительных каналов аппаратуры спутниковой навигации ( GPS , ГЛОНАСС) об относительном расстоянии и относительной скорости аппаратов, входящих в группировку. Целью данного исследования является минимизация расхода топлива на удержание аппаратов вблизи друг друга на заданных непересекающихся финитных траекториях относительного движения при импульсном парировании аэродинамического сопротивления. Исследование проводится методом точечных преобразований и теории бифуркаций [14], при этом особое внимание уделяется одно-импульсным предельным циклам.
Динамика группового полета
Относительное движение рассматривается в орбитальной (опорной) системе координат Хилла: ось OX — вдоль геоцентрического радиуса вектора пассивного КА; ось OY направлена вдоль орбитальной скорости пассивного (опорного) КА; ось OZ дополняет систему до правой тройки.
Для построения релейной системы управления использовалось упрощенное описание динамики относительного движения, определяемое уравнениями HCW :
x – 2 ω y . – 3 ω 2 x = 0,
ӱ + 2ωx. = uy + p, (1) z + ω2z = uz, где uy, uz — компоненты управляющего воздействия; p — аэродинамическое возмущение, действующее на маневрирующий КА; ω — угловая скорость кругового орбитального движения.
При математическом моделировании динамического поведения группировки спутников использовались уже модифицированные [8, 9] уравнения HCW :
6 J 2 ω 2 2 Re 2sin2 i sin(2 θ ) y – 6 J 2 ω 2 2 Re 2 sin2 i sin( θ ) z = 0;
ӱ + 2 ω cx . – J 2 ω e sin2 i sin(2 θ ) x – ω 2 c 2– 1 – J 2 e R 2 R 2
1 +sin2( i ) 1 – 7 sin2 θ y + 6 J 2 ω 2 Re 2 4 2 4 R 2
sin2 i cos θ
4 z = uy + p ;
6 J ω 2 R 2
2 e R 2
sin2 i sin( θ ) x +
6 J ω 2 R 2 2 e
R 2
sin2 i cos θ
y + ω 2
1 + 6 J 2 Re 2 3 – sin 2 ( i ) 1 + 5 sin 2 θ
R 2 4 2 4
z = uz , (2)
где c = 1 + 3 J 2 R e (1 + 3cos2 i ) = 1,0000676;
8 R 2
J 2 = 1,082627⋅10–3.
Траекторию движения маневрирующего КА в плоскости орбиты (плоскости OXY опорной системы координат или картинной плоскости) относительно виртуального КА можно разделить на эллиптическое движение (движение маневрирующего КА по эллипсу относительно опорного) и вековое смещение центра эллипса вдоль оси OY [15]. Для разделения этих двух типов движения производится замена переменных: первая новая пара переменных ξ 1 , ξ 2 отвечает за координаты центра эллипса на картинной плоскости, вторая пара ξ 3 , ξ 4 опр еделяет размер малой полуоси эллипса r = ξ 3 2 + ξ 4 2 . Замена переменных является линейной и описывается следующим преобразованием:
|
ξ 1 |
0 |
–2/ ω |
1 |
0 |
x |
|
|
ξ 2 |
2 |
0 |
0 |
1/ ω |
x. |
|
|
ξ 3 |
= |
3 |
0 |
0 |
2/ ω |
y |
|
ξ 4 |
0 |
1/ ω |
0 |
0 |
. y |
Движение маневрирующих КА относительно оси OZ в линейном приближении представляет собой обычный осциллятор, поэтому для переменных z и z . замены не проводятся.
В новых переменных ξ = [ ξ 1 ξ 2 ξ 3 ξ 4 z z . ] T система уравнений (1) принимает следующий вид:
^ i = 3 to. ,
-
3 2 = ( U y + Р )/ Ю ’
< 4 3 = - ®^ 4 + 2( U Y + Р^ (3)
-
4 4 = Ю^ 3 ’
Z + to2 Z = uz, где первая пара уравнений содержит только переменные ξ1 и ξ2, отвечающие за вековой уход маневрирующего КА относительно начала координат. Вторая пара содержит переменные ξ3 и ξ4, отвечающие за эллиптическое движение маневрирующего КА относительно начала координат. Последнее уравнение описывает движение КА вдоль оси OZ, перпендикулярной плоскости орбиты (cross track motion). Для построения релейного закона управления движением каждого
КА в группировке будем рассматривать отдельно управление по вековому уходу, отдельно — управление эллиптическим движением, и отдельно — в направлении бинормали.
Описание наблюдателя динамического поведения группировки
Наблюдатель предназначен для минимизации ошибок измерений и формирования оценок переменных ξ 1 , ξ 2 , ξ 3 , ξ 4 , по которым формируется управляющий сигнал на исполнительные органы (электро-реактивные двигатели). В данной работе предполагается, что уравнения наблюдателя могут быть запрограммированы в бортовом компьютере каждого аппарата, входящего в группировку. Сами уравнения выводятся при следующих предположениях.
Опорная орбита и положение виртуального центра группировки (реперной точки) на ней задаются и корректируются с наземных пунктов слежения. Далее орбитальные параметры реперной точки передаются в бортовой компьютер одного или нескольких аппаратов группировки, где средствами автономной навигации осуществляются прогноз ее положения на орбите и расчет углового положения опорной системы координат с центром в этой точке относительно системы координат J2000 . Положение маневрирующих аппаратов относительно опорной системы координат определяется с помощью аппаратуры GPS или ГЛОНАСС. Предполагается, что системы управления угловым движением каждого аппарата могут определять и поддерживать свою собственную орбитальную ориентацию с помощью корректируемой бесплатформенной инерциальной навигационной системы [16] и инерционных исполнительных органов.
Управление переменными ξ1 и ξ2.Гашение векового ухода
Рассмотрим первую пару уравнений системы (3)
^ 1 = -3 ю^ 2 ,
^^ 2 = -( и у + Р )/ Ю,
где p — постоянное (усредненное по витку) возмущение от аэродинамического сопротивления; uy = κ ( σ ) — закон релейного управления:
κ ( σ ) = – U , σ > σ 0 , к ( ст ) = 0, | ст| < ст 0 , (5)
κ(σ) = U, σ < –σ0, где U — величина импульса; σ0 — зона нечувствительности; σ = k1ξ1 + k2ξ2 (k1 и k2 — коэффициенты усиления).
При помощи параметризации ζ = ξ 1 k 1 / σ 0 ;
τ = tk 1 / k 2 ; u = σ / σ 0 ; ϑ = dx / d τ приведем систему (4) к следующему виду:
Z = 9,
< 9 = - к ( и ) F - R , (6)
и = Z + H9, где F = –3k22/σ0k1; R = –3pk22/σ0k1; H = –1/3ω.
Решение системы (6) выглядит следующим образом:
I Z = - т 2( к ( и ) F + R )/2 + 9 o T + Z o ,
[ 9 = - т ( к ( u ) F + R ) + 9 0 .
Исключая из решения τ , подставляя вместо κ ( u ) значения из уравнений (5), получаем следующие семейства фазовых траекторий:
-
I: ϑ 2 – ϑ 0 2 = –2( FU + R )( ζ – ζ 0 );
-
II: ϑ 2 – ϑ 0 2 = –2 R ( ζ – ζ 0 );
-
III: ϑ 2 – ϑ 0 2 = –2( R – FU )( ζ – ζ 0 ).
Фазовое пространство системы (4) представляет собой трехлистную плоскость. На каждом из листов определено свое семейство фазовых траекторий, являющихся параболами. Листы ограничены следующими прямыми:
-
• Первый лист: импульс «вперед» — ограничение справа прямой ζ = (– Hs + – 1) – ϑ H ; фазовые траектории — параболы типа I;
-
• Второй лист: движение с выключенным двигателем — ограничение слева прямой ζ = – 1 – ϑ H , справа — прямой ζ = 1 – ϑ H ; фазовые траектории — параболы типа II;
-
• Третий лист: импульс «назад» — ограничение слева прямой ζ = (– Hs – + 1) – ϑ H ; фазовые траектории — параболы типа III.
Параметры s– = –τ0(–UF + R) и s+ = –τ0(UF + R) определяются минимальным временем работы двигателей t0 и величиной импульса электрореактивного двигателя U и, по сути, равны изменению координаты ϑ за время t0 при включении импульса в одну или другую сторону.
Исследование данной релейной системы управления будем проводить, используя метод точечных преобразований, взяв за основу исследования Э.В. Гаушуса, описанные в его монографии [14]. Кратко опишем суть применения метода точечных преобразований в задаче построения релейной системы. Для того чтобы построить оптимальную релейную систему управления, необходимо исследовать на существование и устойчивость различные предельные циклы на фазовой плоскости, к которым в конечном итоге сводится управляемое движение каждого КА. Каждый возможный предельный цикл состоит из нескольких фазовых кривых, которые ограничены линиями переключения на фазовой плоскости. Таким образом, «стартовав» с одной точки одной из линий переключения, за один предельный цикл фазовая траектория вернется в какую-то другую точку на этой линии переключения. Преобразование координаты точки на данной линии переключения за один цикл будем называть точечным преобразованием. Закон, по которому координата точки будет изменяться за предельный цикл, будем называть функцией последования. Варьируя параметры релейной системы переключения, можно качественно менять характер точечного преобразования и, как следствие, тип предельного цикла. Основная задача подобного исследования — используя аналитические выражения, описывающие точечные преобразования, получить область в пространстве параметров релейной системы управления, внутри которой выполнялись бы условия существования и устойчивости необходимого для данной задачи предельного цикла.
Опишем все типы точечных преобразований, участвующие в формировании предельных циклов:
-
• преобразование T 1 прямой ζ = (– Hs + – – 1) – ϑ H в прямую ζ = 1 – ϑ H фазовыми траекториями типа II;
-
• преобразование T 2 прямой ζ = 1 – ϑ H в прямую ζ = (– Hs – + 1) – ϑ H фазовыми траекториями типа III;
-
• преобразование T 3 прямой ζ = (– Hs – + + 1) – ϑ H в прямую ζ = –1 – ϑ H фазовыми траекториями типа II;
-
• преобразование T 4 прямой ζ = –1 – – ϑ H в прямую ζ = (– Hs + – 1) – ϑ H фазовыми траекториями типа I;
-
• преобразование T 5 прямой ζ = (– Hs + – –1) – ϑ H в прямую ζ = –1 – ϑ H фазовыми траекториями типа II.
Наглядно данные преобразования показаны на рис. 1.
'9
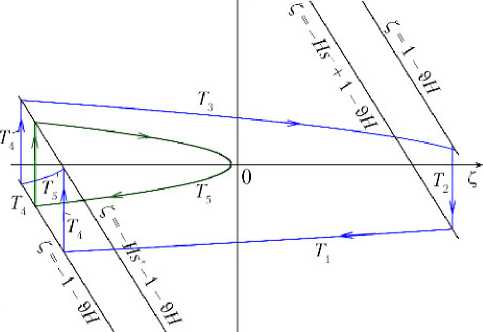
Рис. 1. Точечные преобразования системы и линии переключения в плоскости O ζϑ
Примечание. Ti — название точечного преобразования;
ζ = ±1 – ϑH; ζ = (–Hs+ – 1) – ϑH и ζ = (–Hs– + 1) – ϑH — линии переключения.
Выберем в качестве координаты линий переключений ординату ϑ и обозначим функции последования преобразований Ti , i = 1, 2, …, 5 через α i ( ϑ ). Поскольку любая фазовая траектория исследуемой системы пересекает прямую ζ = (– Hs + – 1) – ϑ H , будем исследовать точечные преобразования данной прямой в себя. Возможны следующие отображения прямой ζ = (– Hs + – 1) – ϑ H в саму себя:
T ε = T 5 T 4 ; T η n ε = ( T 1 T 2 T 3 T 4 ) n T 5 T 4 = ( T η ) n T ε , 7
n = 0, 1, 2, …. (7)
Предельные циклы, соответствующие точечным преобразованиям (7), изображены на рис. 2.
Решая совместно уравнения соответствующего семейства фазовых кривых с линиями переключения и производя замену ψ = ϑ – RH , получаем следующие выражения функций последования для преобразований T 1 , T 2 , T 3 , T 4 , T 5 :
α1(ψ) = ψ2 – 2RHs+ – 4R, а2(у) = — UFH — V [UFH + у]2 + 2Hs-(R - UF),
α3(ψ) = – ψ2 – 2RHs– – 4R , a4W = UFH + V [ UFH - V]= + 2 HS •( R + UF),
α 5 ( ψ ) = – ψ 2 – 2 RHs + .
Точечное преобразование T ε определяет одноимпульсный цикл; преобразование T η n ε — (2 n + 1)-импульсный цикл. Цель — подобрать параметры системы так, чтобы при любых начальных условиях предельный цикл системы сводился к преобразованию T ε . Для этого определим условия, при которых определены преобразования T ε и T η .
Преобразование T η является композицией элементарных преобразований T 1 , T 2 , T 3 , T 4 . Рассмотрим точечное преобразование T 1 и определяющу ю его функцию последования α 1 ( ψ ) = ψ 2 – 2 RHs + – 4 R . Найдем значения переменной ψ , при которых α 1 ( ψ ) не определено. Очевидно, что это происходит в том случае, когда подкоренное выражение в функции α 1 ( ψ ) будет меньше 0, т. е. при ψ 2 – 2 RHs + – 4 R < 0.
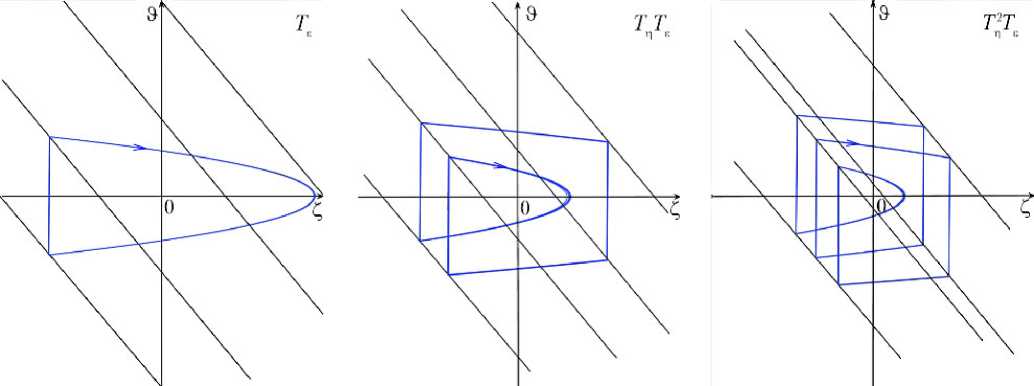
Рис. 2. Вид предельных циклов с преобразованиями T ε , T η T ε , T η 2 T ε на плоскости O ζϑ
Таким образом, преобразование T1 и, как следствие, преобразование Tп будут опре делены при v > \ 2RHs + + 4R; преобра- зование T
Е
при v < \ 2RHs + + 4R. Другими словами, в точке v = V 2 RHs + + 4 R будет происходить бифуркация, т. е. качественный переход от одного точечного преобразования к другому.
Остановимся подробнее на исследовании преобразования Tе. Найдем неподвижные точки данного преобразования, т. е. точки, которые данное преобразование отображают самих в себя. Очевидно, что данные точки находятся из уравнения aE(v) = V, где aE(V) = a4(a5(V)) =
= UFH + V [ UFH + Vw2 — 2 RHs +]2 + 2 Hs + ( R + UF ) .
Решая данное уравнение, нетрудно получить выражение для координаты неподвижной точки преобразования T : V = — s +/2- RH . Е
Наглядно неподвижные точки и сходимость к ним того или иного точечного преобразования можно показать с помощью диаграммы Кенигса–Ламерея (рис. 3), представляющей собой график функции последования V = a ( v ) с нанесенной на нем биссектрисой координатного угла - = v -
Существование неподвижной точки v является одним из необходимых условий сходимости к одноимпульсному предельному циклу. Для того чтобы вывести в пространстве параметров системы условие, при котором существует неподвижная точка у , подставим значение бифуркационной точки v *= V 2 RHs + + 4 R в уравнение аЕ ( у ) = V . Разрешая полученное выражение относительно параметров системы, получаем следующее условие для существования неподвижной точки v и, как следствие, существования одноимпульсного предельного цикла с преобразованием T _ :
s +< –4 R + 2 RH .
Произведя обратную замену переменных, т. е. выражая все через коэффициенты усиления k 1 , k 2 и зону нечувствительности ст 0 , получаем условие зависимости существования одноимпульс-ного цикла от параметров релейной системы:
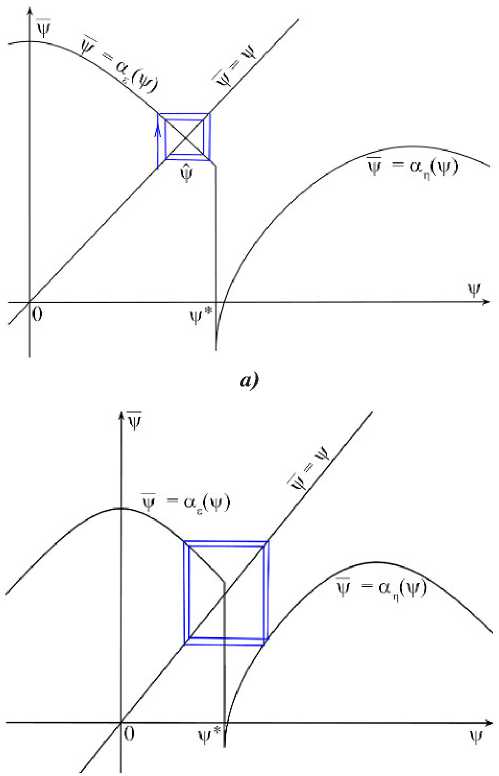
б)
Рис. 3. Диаграмма Кенигса–Ламерея:
а — простой предельный цикл (преобразования T
е
); б — двукратный предельный цикл (преобразования T
е
T
n
);
v
* — точка бифуркации;
а0/ Ц < -3/(16 p )(- t. ( p + U ) + 0 1 0 (8)
+2 p /(3Ю)( k 2 / k 1 ))2.
Рассмотрим второе необходимое условие сходимости фазовых траекторий к одноимпульсному предельному циклу. Для того чтобы система пришла к желаемому устойчивому предельному циклу, необходимо, чтобы точечное преобразование, определяющее предельный цикл, сходилось к своей неподвижной точке. Это условие выполняется при I d а / d vl = |a' ( v ) I < 1, т. е. когда модуль производной функции последования точечного преобразования меньше единицы. В окрестности неподвижной точки \j> = - s +/2 - RH производная функции последования aE ( v ) точечного преобразования T е , определяющего одноимпульсный цикл, имеет следующий вид:
(UFH + I s+/2 - RHI )(s+/2 + RH) а'(ф) =--,=
E I s +/2 - RH I V ( UFH + I s +/2 - RH I )2 + 2 Hs +( R + UF )
или в параметрах k 1 , k 2 и σ 0 , учитывая, что k 1 < 0; k 2 > 0
U tkU 1 tkU1
– 0 1 + 1 + – 0 1+ 1 –
αε′ ( ψ ˆ) = –
3ωp 2 k2 p 3ω 2 k2 p3
tk U 1 U tk U1
0 1 + 1 + – – 0 1+ 1 –
Чем меньше по модулю значение производной αε′ в окрестности точки ψ ˆ , тем быстрее происходит сходимость точечного преобразования к неподвижной точке, и, как следствие, система быстрее приходит к устойчивому предельному циклу. Очевидно, что наилучшая сходимость происходит при αε′ ( ψ ˆ ) = 0.
Требуется подобрать значения k 1 и k 2 , при которых выполняется данное равенство. Решая уравнение αε′ ( ψ ˆ ) = 0 относительно переменной k 2 / k 1 , получаем следующее выражение для значений параметров системы, при которых выполняется условие наилучшей сходимости:
k 1 / k 2 = - 3 ю 1 0 ( U / p + 1)' (9)
Таким образом, выведено два основополагающих условия для выбора параметров системы. Первое условие (8) — для обеспечения существования простой неподвижной точки и, как следствие, для обеспечения одноимпульсного предельного цикла, обеспечивающего минимальный расход топлива; второе условие (9) — для обеспечения наилучшей сходимости фазовых траекторий к желаемому предельному циклу:
σ 0 / k 1 < –3/(16 p )(– t 0 ( p + U ) + 2 p /(3 ω )( k 2 / k 1 ))2;
k 2 / k 1 = –2/(3 ω t 0 ( U / p + 1)). (10)
Решая систему уравнений (10) относительно переменных k 2 / k 1 и σ 0 / k 1 , получаем следующие выражения для оптимального выбора параметров релейной системы управления:
k 1 / k 2 = –2 p /(3 ω t 0 U );
σ 0 / k 1 = –3( t 0 U )2/(4 p ).
Учитывая значения U , p , ω , h 0 , выражения (11) примут следующий вид:
k 1 / k 2 = –0,045; σ 0 / k 1 > 20 м.
Определим период устоявшегося одно-импульсного цикла с преобразованием T ε = T 5 T 4 . Предельный цикл состоит из двух частей: движение с включенным двигателем (точечное преобразование T 4 с функцией последования α 4 ( z )) и движение с выключенным двигателем (точечное преобразование T 5 с функцией последования α 5 ( z )), поэтому период предельного цикла можно представить как T = Timpuls + Tfree .
Очевидно, что время движения КА с включенным двигателем равно минимальному времени работы двигателя, т. е. Timpuls = τ0 = –t0 k1/k2. Время Tfree выражается из решения исходной системы ϑ = –τ(κ(u)F + R) + ϑ0 путем подстановки вместо переменных ϑ и ϑ0 значений неподвижных точек ϑ1 = –τ0(UF + R) и ϑˆ2 = τ0(UF + R), соответственно (точки ϑˆ 1 и ϑ2 являются, соответственно, неподвижными точками преобразований T5T4 и T4T5); κ(u) = 0; τ = Tfree. Для времени движения КА с выключенным двига- телем получаем следующее выражение: Tfree = –τ0(UF/R + 1). Таким образом, период предельного цикла T равен: T = Timpuls+Tfree = –τ0UF/R, или, выражая через «старые» переменные:
T0 = t 0U/p, где p — величина постоянного возмущения; t0 — минимальное время работы двигателя. Характеристическая скорость, определяющая расход топлива за фиксированный период T = nT0, где n ∈ N, будет равна ΣVT = pT.
Как м 0 ожно видеть, расход топлива при одноимпульсном предельном цикле зависит только от величины возмущения. Подставляя значения величин t 0 = 10 c; U = 0,0002 м/с2 и paer = 1,52⋅10–7 м/с2 в полученные выражения, получаем оценку времени для периода предельного цикла T 0 = 2,3 витка и оценку годовой характеристической скорости Σ Vyear = 4,8 м/с.
Управление переменными ξ 3 и ξ 4.
Выведение маневрирующего КА на эллипс с заданным размером. Управление КА вдоль поперечной оси OZ
Рассмотрим вторую пару уравнений системы:
^ 3 = - Ю^ 4 + 2( к ( ^ ) + Р )/ ® >
^ 4 = ®^ 3 ’
здесь переменные ξ 3 и ξ 4 отвечают за эллиптическую составляющую вращения маневрирующего КА относительно опорного КА; p — постоянное возмущение; κ ( σ ) — релейный закон управления.
Решение системы (12) и семейства фазовых траекторий выглядит следующим образом:
- = ^ 30 sin (ro t ) - (2(к(^) + p Но 2 - ^40)cos(® t ) +
< + 2(k(o) + p Но2 ,
^ 3 = ^ 3o COs (to t ) + (2(k(q) + p )/to 2 - ^ 4o )sin( to t );
-
I: ξ 3 2 + ( ξ 4 – 2( U + p )/ ω 2)2 = = ξ 2 30 + ω 2( ξ 40 – 2( U + p )/ ω 2)2;
-
II: ξ 3 2 + ( ξ 4 – 2 p / ω 2)2 = ξ 30 2 + ( ξ 40 – 2 p / ω 2)2;
-
III: ξ 3 2 + ( ξ 4 – 2( p – U )/ ω 2)2 =
= ξ 2 30 + ( ξ 40 – 2( p – U )/ ω 2)2.
Как можно видеть, фазовые траектории представляют собой три набора концентрических окружностей с центрами в точках [2( U + p )/ ω ; 0], [2 p / ω ; 0], [2( p – U )/ ω ; 0], соответственно.
Введем параметр r = ξ 3 2 + ξ 4 2 , определяющий величину малой полуоси эллипса движения маневрирующего КА относительно опорного. Добавим в существующий закон управления по гашению векового ухода весовые коэффициенты, отвечающие за эллиптическое движение и зависящие от величины r :
σ = k 1 ξ 1 + k 2 ξ 2 + k 3 ( r ) ξ 3 + k 4 ( r ) ξ 4 ;
k(q) = - и , о > o 0 ,
< k(o) = 0, |о| < о0, k(o) = и, о < -о0, где k3, k4 — коэффициенты усиления; σ0 — зона нечувствительности. Зависимость коэффициентов k3 и k4 от r зададим следующим образом:
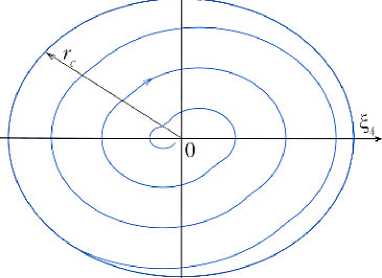
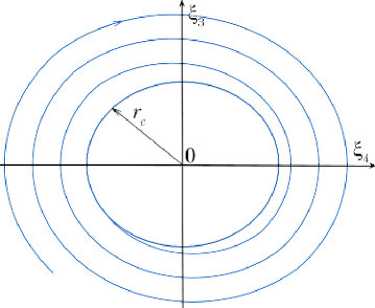
k3(r) ≥ 0, k4(r) ≥ 0, r < rc – σr, k3(r) = 0, k4(r) = 0, rc – σr < r < rc + σr, k3(r) ≤ 0, k4(r) ≤ 0, r > rc + σr, где rc — малая полуось целевого эллипса; σr — ширина области, которая определяет точность выведения маневрирующего КА на эллипс с заданным размером. Наглядно эти величины можно представить на фазовой плоскости ξ3ξ4 (рис. 4)
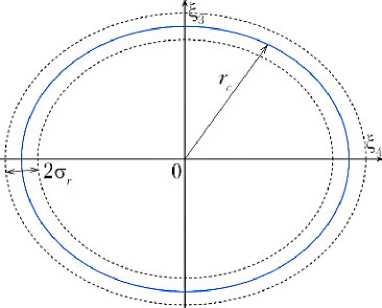
а)
б)
в)
Рис. 4. Фазовая плоскость ξ 3 ξ 4: а — целевой размер эллипса rc и ширина «зоны нечувствительности» σ r; б, в — фазовые кривые, описывающие движение маневрирующего КА при различных значениях величины r
В зависимости от того, в какой области на фазовой плоскости 5 3 5 4 в данный момент находится КА, подбираются соответствующие коэффициенты усиления:
-
• объект на фазовой плоскости 5 3 5 4 находится внутри окружности радиуса ( rc - о r ) — k 3 ( r ) > 0; k 4 ( r ) > 0 — «раскачивание осциллятора» до нужной амплитуды, равной rc (размер малой полуоси целевого эллипса);
-
• объект на фазовой плоскости 5 3 5 4 находится вне окружности радиуса ( r c + о r ) — k 3 ( r ) ≤ 0; k 4 ( r ) ≤ 0 — уменьшение амплитуды колебаний до rc ;
-
• объект на фазовой плоскости 5 3 5 4 находится внутри кольца , ограниченного окружностями с радиусами ( rc - о r ) и ( rc + о r ) — к 3 ( r ) = 0; к 4 ( r ) = 0 — движение объекта по эллипсу с размером, близким к целевому ( rc ± о r ).
Как только на фазовой плоскости 5 3 5 4 объект попадает в кольцо ( rc ± о r ), коэффициенты усиления k 3 и k 4 становятся равными нулю, система управления принимает следующий вид:
о = k 1 5 1 + k 2^ ;
к(о) = - и, о > о0, < к(о) = 0, |о| < о0, к(о) = и, о < -о0, и топливо тратится только на гашение векового ухода.
Поскольку структура линеаризованных уравнений движения маневрирующего КА вдоль оси OZ ( cross track motion ) аналогична уравнениям (12), то принцип управления движением аппаратов вдоль поперечной оси будет также аналогичен управлению по переменным 5 3 и 5 4 .
Результаты математического моделирования
Математическое моделирование относительного движения группировки КА проводилось в среде MATLAB . Моделирование проводилось для группировки, состоящей из трех маневрирующих спутников. Для имитации реального динамического поведения группировки КА с учетом возмущений в качестве уравнений движения использовалась система уравнений (2). Для численного интегрирования уравнений движения использовался метод Рунге–Кутты, реализованный в MATLAB в виде функции ode45 .
Начальные координаты и начальные ско рости спутников имели следующие значения:
|
x 1 |
0м |
|
|
x . 1 |
0м |
|
|
y 1 |
0м |
|
|
y . 1 |
= |
0 , 2 м / c |
|
z 1 |
0м |
|
|
. z 1 |
0,1 м/c |
|
x 2 |
0м |
|
|
x . 2 |
0м |
|
|
y 2 |
0м |
|
|
y . 2 |
= |
0 , 2 м / c |
|
z 2 |
0м |
|
|
z . 2 |
0 м |
|
x 3 |
0м |
|
|
x . 3 |
0м |
|
|
y 3 |
0м |
|
|
y . 3 |
= |
0 , 2 м / c |
|
z 3 |
0м |
|
|
z . 3 |
0м |
Конечные условия для положения спутников:
yc 1 = 51 = 0 м, yc2 = 51 = 0 м, yc3 = 51 = 0 м, xc 1 = 52 = 0 м, xc2 = 52 = 0 м, xc3 = 52 = 0 м, rc1 = ξ32 + ξ42 = 250 м, rc2 = ξ32 + ξ42 = 500 м, rc3 = ξ32 + ξ42 = 750 м, rcz1 = 500 м, rcz2 = 0 м, rcz3 = 0 м, где yci и xci — координаты центров эллипсов каждого маневрирующего КА; rci = ξ32i + ξ 42i — размер малой полуоси эллипса для каждого аппарата; rczi — максимальное смещение каждого аппарата относительно поперечной оси OZ.
Параметры опорной орбиты: радиус R = 6,89⋅106 м; эксцентриситет e = 0; наклон орбиты i = 5 ° ; орбитальная угловая скорость ю = 0,001103 рад/с. Влияние сжатости Земли: J 2 = 1,0826⋅10–3.
Минимальное время работы двигателя и величина импульса, соответственно, равны: h 0 = 10 c; U 0 = 0,0002 м/с2.
Масса каждого КА принималась равной m = 2⋅103 кг; орбитальная скорость опорного КА V = 7,67⋅103 м/с; эффективная площадь КА S = 20 м2; плотность атмосферы (высота 512 км) р = 5,21-10-13 кг/м3; аэродинамическое сопротивление p =1,52⋅10–7 м/с2.
Параметры релейной системы управления были подобраны с учетом результатов исследований, проведенных в работе, и имели следующие значения:
-
• по переменным 5 1 и 5 2 : к 1 = -0,0045 c-2; к 2 = 0,1 c-2; о 0 = 0,1 м/с2;
-
• по переменным 5 3 и 5 4 : о = 20 м; k 3 = 0 c–2; k 4 = 0±0,002 c–2; r
-
• по переменным z и Z : о = 1 м; k 5 = 0±0,001 c–2; k 6 = 0±2,5 c–1. z
Результаты математического моделирования представлены на рис. 5–7.
а)
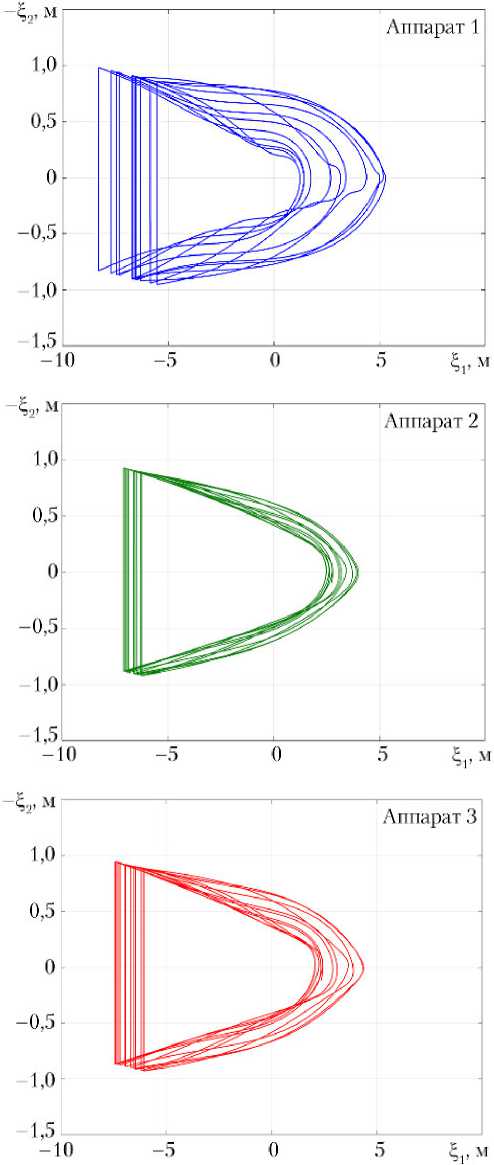
-
б)
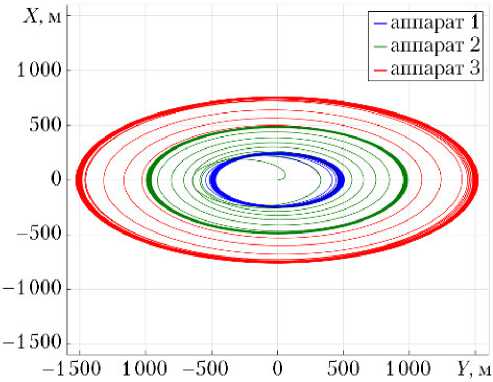
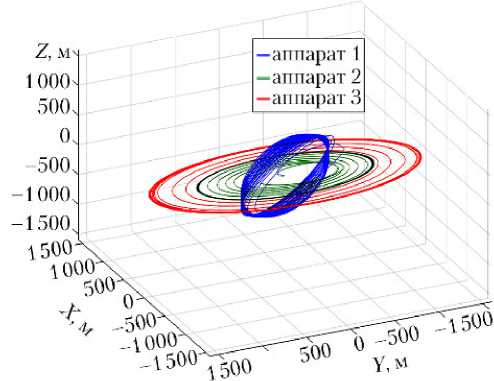
относительно опорного: а
в проекции на картинную
Рис. 5. Траектории движения маневрирующих спутников плоскость OXY; б — в пространстве OXYZ
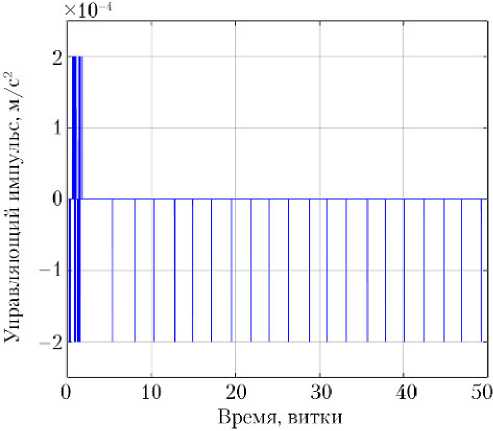
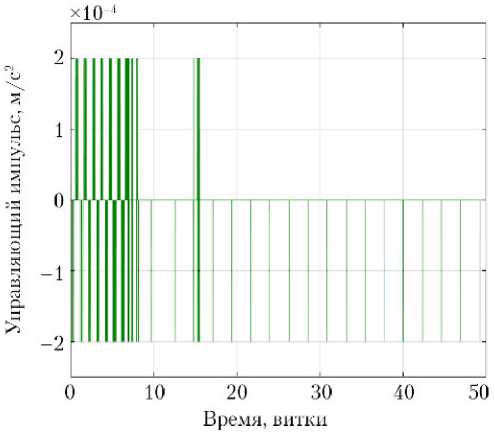
-
а)
б)
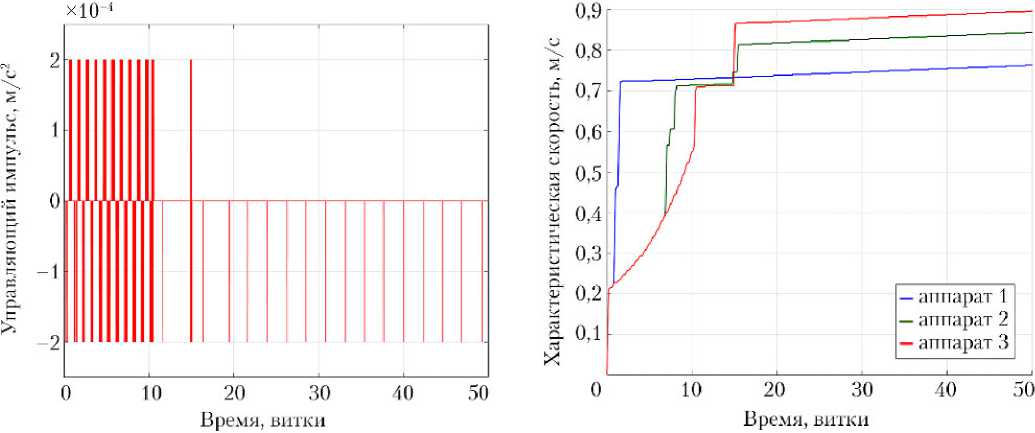
в)
г)
Рис. 6. Импульс, подаваемый электрореактивным двигателем: топлива (характеристическая скорость каждого КА)
а, б, в — Uy для каждого из трех КА; г — суммарный расход
Результирующий предельный
Рис. 7. Фазовая плоскость. цикл для переменных ξ 1 и ξ 2
Заключение
В данной работе предложен и исследован релейный закон управления относительным движением группировки спутников, находящихся на расстоянии до 2 км друг от друга на орбитах, близких к круговым. В ходе исследования релейной системы управления методом точечных преобразований были получены аналитические соотношения для параметров данной релейной системы, обеспечивающие одноимпульсный предельный цикл и, как следствие, — минимальный расход топлива каждым КА для парирования аэродинамического возмущения. На основе результатов данного исследования был построен алгоритм управления, позволяющий выводить каждый КА на финитную относительно опорной точки траекторию с заданными параметрами, и удерживать его на ней. Для верификации разработанного релейного алгоритма управления было проведено математическое моделирование динамического поведения группировки, состоящей из трех маневрирующих КА. Результаты моделирования показали, что каждый аппарат вышел на эллиптическую относительно опорной точки траекторию с заданными параметрами, а расход топлива для поддержания каждого КА на заданной траектории близок к теоретически рассчитанному.
Работа выполнена при финансовой поддержке РФФИ, в рамках научного проекта № 17-08-01635, 18-08-01379.
Список литературы Релейная автономная система управления группировкой спутников, базирующейся на низкой околоземной орбите
- Bauer F.H., Hartman K, How J.P., Bristow J., Weidow D., Busse F. Enabling spacecraft formation flying through spaceborne GPS and enhanced automation technologies // ION-GPS '99 Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation, September 14-17, 1999. P. 369-383.
- Hill G.W. Researches in Lunar Theory // American Journal of Mathematics. 1878. V. 1. P. 5-26.
- Clohessy W.H., Wiltshire R.S. Terminal guidance system for satellite rendezvous // Journal of the Aerospace Sciences. 1960. V. 27. № 9. P. 653-658.
- Chichka D.F. Satellite cluster with constant apparent distribution // Journal of Guidance, Control and Dynamics. 2001. V. 24. № 1. P. 117-122.
- Schaub H. Relative orbit geometry through classical orbit element differences // Journal of Guidance, Control and Dynamics. 2004. V. 27. № 5. P. 839-848.
- Amico S.D., Montenbruck O. Proximity operations of formation-flying spacecraft using an eccentricity/inclination vector separation // Journal of Guidance, Control and Dynamics. May-June 2006. V. 29. № 3. P. 554-562.
- Сихарулидзе Ю.Г. Баллистика летательных аппаратов. М.: Наука, 1982. 352 с.
- Schweighart S.A., Sedwick R. J. High-fidelity linearized J2 model for satellite formation flight // Journal of Guidance, Control and Dynamics. November-December 2002. V. 25. № 6. P. 1073-1080.
- Schweighart S, Sedwick R.J. Cross -track motion of satellite formations in the presence of J2 disturbances // Journal of Guidance, Control and Dynamics. 2005. V. 28. № 4. P. 824-826.
- Roberts J.E., Roberts P.C.E. The development of high fidelity linearized J2 models for satellite formation flying control // In Advances in the Astronautical Sciences. Part I: Spaceflight Mechanics. 2004. V. 119. P. 913-933.
- Leonard C.L., Hollister W.M. and Bergmann E.V. Orbital formation keeping with differential drag // AIAA Journal of Guidance, Control and Dynamics. 1989. V. 12. P. 108-113.
- Kapila V., Sparks A.G., Buffington J.M. and Yan Q. Spacecraft formation flying: dynamics and control // Journal of Guidance, Control and Dynamics. 2000. V. 23. № 3. P. 561-564.
- Flügge-Lotz I. Discontinuous automatic control. Princeton: N.Y. Princeton Univ. Press, 1953. 168 p.
- Гаушус Э.В. Исследование динамических систем методом точечных преобразований. М.: Наука, 1976. 368 с.
- Аппазов Р.Ф., Сытин О.Г. Методы проектирования траекторий носителей и спутников Земли. М.: Наука, 1987. 440 с.
- Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных навигационных систем. М.: Наука, 1992. 280 с.


