Reliability-based topology optimization using two alternative inverse optimum safety factor approaches: application to bridge structures

Topology optimization tries to answer one of the first structural issues to fulfill the necessary technical specifications. So the topology problem consists of determining the structure’s general characteristics, and the objective of topology optimi-

Mechanical engineering zation is to make that initial choice as automatically as possible [1]. Furthermore, in topology optimization, both macroscopic structures and microscopic materials can be found. In other words, not only the optimal spatial material distribution at the macroscopic structural scale is found, but also the optimal local use of the cellular material at the microscopic scale [2].

Two major forms of topology optimization may be distinguished, in literature: deterministic form (DTO: Deterministic Topology Optimization) and probabilistic one (RBTO: Reliability-Based Topology Optimization). In the deterministic form, it can be generated a single configuration for a particular given parameter space [3]. While, when the probabilistic form is considered, several configurations can be obtained with different advantages. It helps the designer to select the best configuration to realize the technical specifications. The weight of the resulting configurations produced by the RBTO strategy is minimized when compared with the deterministic one. Additionally, the use of the RBTO strategy and for the same structural weight, the obtained structure is more reliable than the deterministic one [4]. The different RBTO developments can be classified according to two points of view: topology optimization and reliability analysis. The interested reader can find a detailed review in [5]. It has been established that the different developments from point of view “topology optimization” can be considered as an attractive point for topology designers since it leads to a number of reliability-based topologies with respect to the reliability index variation. It provides diverse layout structures, however, the different advances from the “reliability analysis” point of view yields to the same configurations with different densities that do not have any importance for the following design steps [6–9]. Thus, in the following section, a literature of the different advances from a point of view “topology optimization” is presented to focus on the advantage of the developed methods [10].

Literature Review

M. P. Bendsoe and N. Kikuchi were the first who integrated the homogenization approach into the optimal material distribution study [1]. The majority of topology optimization studies were based

Том 30, № 3. 2020

on the deterministic assumption. To study the uncertainty effect in the topology optimization, G. Kharmanda and N. Olhoff were the first who incorporated reliability constraints into DTO studies [11]. The approach starts with a sensitivity evaluation of the objective function with respect to different parameters in order to identify the random variables that have a large influence on the objective function. This elaborated model provides the designer with several reliability-based structures however in the classical DTO, a single deterministic topology is produced. The value of the RBTO concept is to provide structures that should be more reliable than those generated using DTO. After that, the authors applied probabilistic neural networks for highly nonlinear or disjoint failure domain problems [12]. Next, developed a non-probabilistic RBTO approach for the detailed design stage of continuum structures, in which the unknown but bounded uncertainties that exist in material and external loads were simultaneously considered [13]. Recently Inverse Optimum Safety Factor (IOSF) strategy was proposed to deal with the modal studies where there are no external loads and the topology optimization integration into free vibrated structures may provide unworkable topologies [5]. The IOSF strategy implementation was limited to consider the parameterization only on the optimization domain.

In order to execute an RBTO problem, there are many Reliability-Based Design Optimization (RBDO) techniques that can be carried out. According to the application areas, some RBDO approaches have been used [4]. For example, the Optimum Safety Factor (OSF) approach as an efficient RBDO technique has been applied in a simple way considering two simple steps [4]. The first step is to use a single simplified optimization procedure in order to find the failure point; however, the next step is to use the OSF equations to evaluate the optimum solution. An Inverse Optimum Safety Factor (IOSF) approach was developed to first determine the topology configuration by DTO procedure [5]. After that, the OSF equations are performed considering inverse signs of the derivatives in order to produce diverse RBTO layouts. The generation of the resulting topology layouts is carried out considering a given design space (geometry, loading, material properties, etc.). In this work, two alternative IOSF approaches are developed to produce two categories (families) of solutions that can open more possibilities for the designer to choose the best configuration which can be the most advantageous solution. Two numerical studied cases on a 2D bridge structure are detailed where the topology optimization problem is modeled in two different ways.

Materials and Methods

Deterministic topology optimization In this work, the problem of topology optimization is described in two different ways. The first way is to reduce the structural compliance under a required ratio reduction of volume V_f ^r . The problem of DTO model is then mathematically written by:

min : C ( x )

‘ . t . : VVx ) £ V f .     (1)

where C ( x ) is the structural compliance where the densities of the used material in each element are considered as optimization variables. Their values should be in the interval [0, 1]. V ⁰ and V ( x ) are the initial – and present (or current) structural volume values. However, the second way is to reduce the volume under a required ratio increase of compliance C_f ^r [14–18]. The DTO problem is then mathematically formulated as follows:

min : V ( x )

• 5 .    t . : C^x) < 1 + C r ,    (2)

• 5 .    t : H(u ) = 0 ,        (3)

where V(x) is the structural volume considering the material densities in each ele-Mechanical engineering ment as optimization variables that belong to the interval [0, 1]. С0 and C(x) are the initial – and current structural compliance values [19–23]. Formulations 1 and 2 are fundamental forms and can be implemented with some topology optimization approaches such as SIMP (Solid Isotropic Microstructure with Penalty), homogenization approach and many recent methods have been recently developed to extend the topology optimization to some advanced area such as additive manufacturing [24–26].

Reliability Index

In order to generate the resulting topologies, a reliability index β is used with a normalized vector u . Figure 1 shows the transformation image between the random variables y in the physical space and the normalized vector u in the normalized space [27]. The general reliability index evaluation can be performed using the following optimization problem:

в = min d ( u )

where the distance d ( u ) in the normalized space is given by:

d ( u ) = u 1 + ... + и П .    (4)

The optimum value of β corresponds to the Most Probable failure Point (MPP) which is represented by the minimum distance between the origin of the normalized space and limit state curve as shown in Fig. 1. The reliability index assessment is carried out using FORM (First Order Reliability Method).

The reliability index values affect the conceptual design stage. The validation of this effect is studied by [28]. In general, the nuclear and spatial applications require very small values of failure probability, the failure probability has to be: P f ϵ [10^–6 – 10^–8] which corresponds to a reliability index interval β ϵ [4.75 – 5.6],

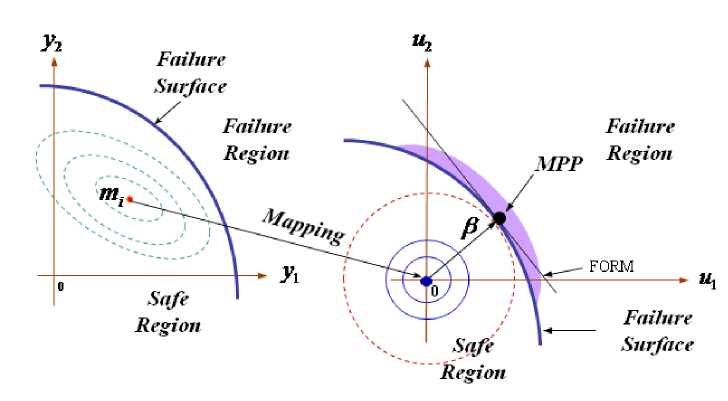
F i g. 1. Transformation image between the physical space and the normalized one

while in civil engineering, the failure probability has to be: P f ϵ [10^–6 – 10^–5] which corresponds to a reliability index interval β ϵ [3 – 4.25]. For structural engineering applications, the used target reliability index is: β = 3.8. A detailed revision of target reliability indices can be found in [29].

RBTO by Objective-Based IOSF Approach

The previous OSF strategy can efficiently decrease the size of the RBDO problem using the sensitivities of the limit state function with respect to all the structure’s parameters, especially when the sensitivity can be calculated analytically [30; 31]. The main idea of OSF strategy is to find the failure point and next the optimum solution using the OSF formulations. The problem of RBTO model is to reduce the structural compliance und _r a required ratio reduction of volume V f^r and the reliability constraint. The RBTO problem is then mathematically formulated by:

min : C (x)5. t. : в ^ et

and : VVx) s Vf,      (5)

where β_t is the required reliability index to be respected. The failure is related to the compliance. In this case, the compliance is considered as an objective function. Thus, the sensitivity can be estimated considering the objective function as a failure criterion. This way, the optimum value of the normalized vector can be expressed by:

U = ± et

∂F ∂yi

.

n

∂F ∂yj

According to the derivative sign of the objective function with respect to random variables y_i , we have:

— > 0 ^ ui > 0 and dVi

dF — <

dy,

0 ^ u* < 0.

This approach takes into account both concepts of the OSF and failure criterion. When the failure criterion is treated as an

objective function, the Objective-Based IOSF Approach can be implemented, however when the failure criterion is treated as a performance function, the method can be called Performance-Based IOSF Approach, which is presented in the following section.

RBTO by Performance-Based IOSF Approach

The different developments of the OSF strategy for linear and nonlinear distribution laws are carried out considering the structural reliability philosophy. These developments fit with the fundamental idea of this proposed approach where the structural compliance is considered as a performance function (constraint function). Thus, the RBTO problem is to minimize the structural volume subject to the compliance constraint and the reliability one. The RBTO problem is then mathematically formulated by:

min : V (x)5.    t. : в ^ et

and : CT ^ 1 + CT.   (8)

The optimum value of the normalized vector can be written as follows:

*

u_i =± β_t

∂ G ∂ y_i

n ∑ j = 1

∂ G ∂ y j

According to the derivative sign of the limit state function with respect to random variables y i , we have:

⁸-G >  о ^дУ,

u * >  0 and

d G

— < дУ,

Here, the random variable vector is considered to be normally distributed, the safety factor can be formulated as follows:

Sfi = 1 + Y • u*, (11)

where the relationship between the mean m_i and standard-deviation ϭ_i is represented by the variance coefficient γ_i as follows:

Y i = o i / m i . (12)

In both developed approaches, the starting point is considered as the failure point P* and the determination of the reliability-based topology P X is next carried out. The reliability-based topology P X should be more reliable than the failure point P y and should also verify a target reliability index β_t . This way the DTO procedure is used to determine the failure point P y and the both developed approaches are then used to find the reliability-based topologies P_x .

Results

The topology optimization is applied here to a 2D bridge structure considering two studied cases: the first case is to minimize the structural compliance C ( x ) subject the constraint of the volume reduction ratio V_f (1) and (5). However, the second case is to minimize the structural volume V ( x ). Subject the constraint of the compliance increase ratio C_f (2) and (8). It is the objective to find the best distribution of material considering three studies: DTO, RBTO using Objective-Based IOSF approach, and RBTO using PerformanceBased IOSF approach.

The initial domain is represented by a rectangle (200 × 50 m). As shown in Figure 2, two domain are considered: the lower domain is not considered to be optimized (200 × 7.5 m), while the upper domain is considered as optimized domain (200 × 42.5 m). The bridge is considered to be made of steel with a Young’s modulus E = 200 000 MPa and a Poisson’s ratio v = 0.3. The material behavior is linear

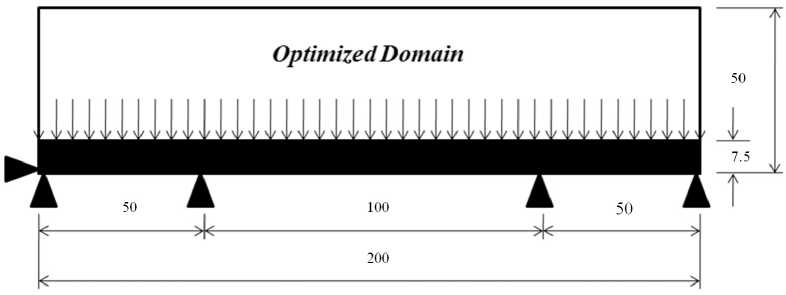
F i g. 2. Initial configuration of the studied 2D bridge structure

elastic isotropic. The applied distributed force is: F = 1 × 10⁸ N/m. The boundary conditions are illustrated in Figure 2. To perform the RBTO using Objective-Based and Performance-Based IOSF Approaches, the sensitivity evaluation is carried out on the starting point configuration and considering the central finite difference approach as an accurate tool for sensitivity analysis.

First category of solutions

The starting configuration is considered to be the failure point where the optimization problem is to minimize the structural compliance subject to the volume constraint for the DTO (1) and also the reliability constraints for the RBTO (5).

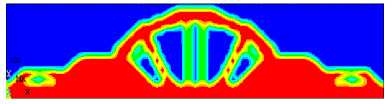
Figures 3a, 3b and 3c show the resulting 2D bridge topologies when considering the compliance as an objective function for DTO model (failure point P y ) and RBTO models when the reliability indices are: β t = 3, and β t = 3.8 using ObjectiveBased IOSF approach. The corresponding resulting compliances are shown in Table 1 for the initial configuration C ⁰ and the optimal one C ^*. The used number of element for optimization is 1 360 nonlinear elements (PLANE82 with 8-nodes) and the Optimality Criteria (OC) method which implemented in ANSYS Software is used. The uncertainty is considered on the loading, the material properties and the volume reduction ratio (quantity of

a)

b)

c)

F i g. 3. Resulting 2D bridge topologies when considering the compliance as an objective function:

• a) DTO configuration; b) RBTO configuration for β_t = 3;

c) RBTO configuration for βt = 3.8 using Objective-Based IOSF approach materials). The random variables are: E, v, F and Vf . The standard deviations are assumed to be proportional to the starting values (Py*) presented in Table 1, i.e. ϭi = γimi (12), where γi = 0.1.

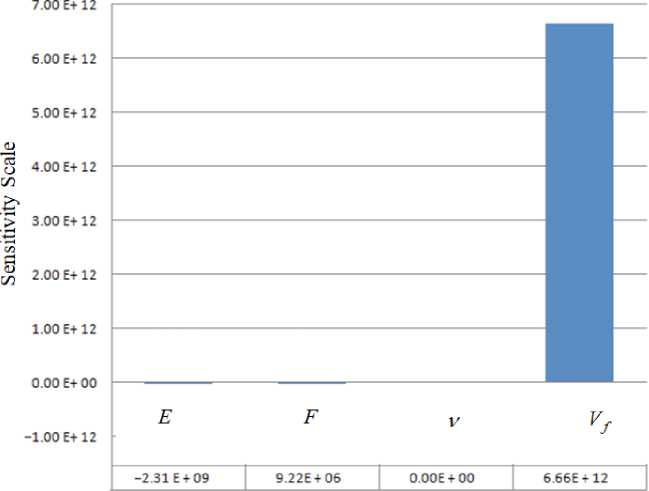
Figure 4 shows the sensitivity magnitude values of the compliance with re- spect to the four random variables where the compliance is treated as an objective function.

The input and output parameters are shown in Table 1 where the compliance as an objective function. In this table, the failure point P_y ^* and the optimum solution

ас

Exact Sensitivity Values: ——

F i g. 4. Sensitivity magnitude values of the compliance as an objective function

T a b l e 1

Different input and output parameters for the first category of solutions

Parameters	P y *	β = 3			β = 3.8
		u i	S fi	P x *	u i	S fi	P x *
E	200 000	–0.05582	0.99442	198 883.64	–0.0707	0.99293	198 585.94
F	1 × 108	0.00353	1.00035	100 035 301	0.0045	1.00045	100 044 714
v	0.3	0	1	0.3	0	1	0.3
V f	50	2.99948	1.29995	64.997393	3.7993	1.37993	68.996698
C 0	12.066 × 1016	19.722 × 1016			22.968 × 1016
C*	4.6095 × 1014	5.9892 × 1014			6.5099 × 1014
V ( x )	4 250	2 975.22			2 635.28

P_x ^* for two chosen target reliability indices ( β = 3 and β = 3.8) are presented. The normalized vector u_i is calculated using (6) and the corresponding safety factors S_f are computed using (11).

Second category of solutions

The starting configuration is considered to be the failure point where the problem is to minimize the structural volume subject to the compliance constraint for the DTO (2) and also the reliability constraints for the RBTO (8). Figures 4a, 4b and 4c show the resulting 2D bridge topologies when considering the structural volume as an objective function for DTO model (failure point P_y ^* ) and RBTO models when the reliability indices are: β t = 3, and β t = 3.8 using Performance-Based IOSF Approach. The corresponding resulting volumes are shown in Table 1 for the initial configuration V ⁰ and the optimal one V* . The used number of element for optimization is 1 360 nonlinear elements (PLANE82 with 8-nodes) and the Sequential Convex Programming (SCP) method which implemented in ANSYS Software is used. The uncertainty is considered on the material properties, the loading and the compliance increase ratio C f . The random variables are: E , v, F and C f . The standard deviations are assumed to be proportional to the starting values ( P y ) presented in Table 2, i.e. ϭ i = γ i m i (12) where γ = 0.1.

Том 30, № 3. 2020

The sensitivity values of the compliance as a performance function with respect to the four random variables are shown in Figure 6.

The input and output parameters are shown in Table 2 where the compliance as a performance function. In this table, the failure point P_y ^* and the design point P_x ^* for two chosen target reliability indices ( β_t = 3, and β_t = 3.8) are presented. The normalized vector u_i is calculated using (9) and the corresponding safety factors S f_i are computed using (11).

Discussion and Conclusion

According to our previous work, the Inverse Optimum Safety Factor (IOSF) method has been successfully used for free vibrated structures [5]. The used random parameters concerned the external geometrical boundaries. In this work, the uncertainty is applied to material properties, loading and response parameters. Two alternative IOSF approaches are developed to provide two categories of solutions. The resulting topology configurations, sensitivity values and output parameters are clearly different for the same given space. The influence of the input parameter is determined using sensitivity analysis being the basic tool of the OSF strategy. The starting point is represented by the failure point P_y ^* , and from this point, the reliability level should be increased.

a)                                                        b)

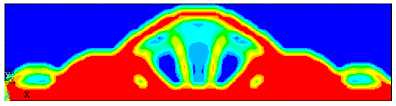
c)

F i g. 5. Resulting 2D bridge topologies when considering the structural volume as an objective function: a) DTO configuration; b) RBTO configuration for β_t = 3; c) RBTO configuration for β_t = 3.8 using Performance-Based IOSF approach

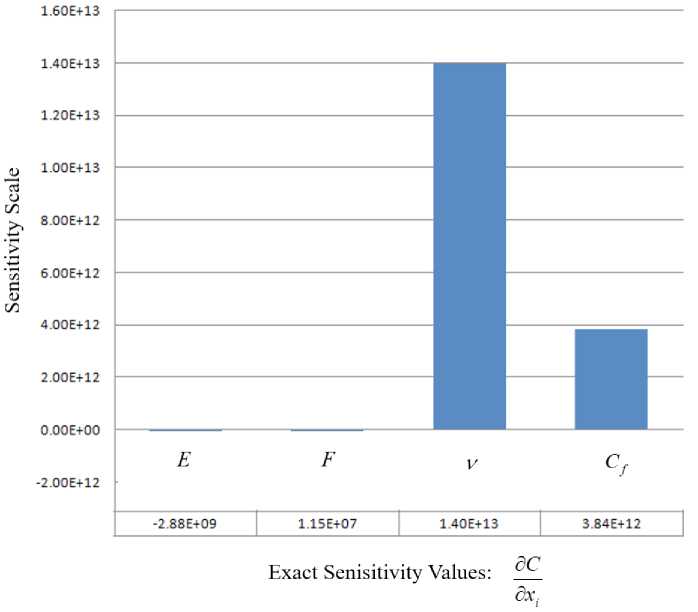
F i g. 6. Sensitivity magnitude values of the compliance as a performance function

T a b l e 2

Different input and output parameters for the second category of solutions

Parameters	P y *	β t = 3			βt = 3.8
		u i	S f i	P x *	u i	S f i	P x *
E	200 000	–0.03810	0.996190	199 238	–0.04826	0.995174	199 034.8
F	1 × 108	0.00241	1.000241	100 024 100	0.00306	1.000306	100 030 600
v	0.3	2.65760	1.265760	0.379728	3.36629	1.336629	0.400989
C f	50	1.39130	1.139130	56.9565	1.76231	1.176231	58.81157
V 0	8 500
V *	3 148.39	2 926.11			2 874.46
C ( x )	5.7483 × 1014	6.2735 × 1014			6.4130 × 1014

In the Objective-Based IOSF Approach, the compliance is considered as an objective function and its sensitivity is evaluated with respect to different parameters. It provides the first category of RBTO solutions when changing the reliability index values. It is noted that the volume fraction has the biggest role on the resulting compliance, while the Poisson’s ratio has no influence on the resulting compliance (Fig. 4). The resulting RBTO configurations (Fig. 3b and 3c) can be modeled with a bigger number of holes in the structure. This result can be supported numerically by the decrease of the structural volume V ( x ), when increasing the reliability index values (Table 1).

However, in the Performance-Based IOSF Approach, the compliance is considered as a performance function and its sensitivity is evaluated with respect to different parameters. It provides the second category of RBTO solutions when changing the reliability index values. It is noted that the Poisson’s ratio has the biggest

Том 30, № 3. 2020

role on the resulting compliance which is totally different when using the previous alternative approach (Fig. 6). The resulting RBTO configurations (Fig. 5b and 5c) can be also modeled with a bigger number of holes in the structure. This result can be supported numerically by the decrease of the optimal values of the structural volume V ^*, when increasing the reliability index values (Table 2). It is noted also that when the reliability index equal to β_t = 3.8, the Poisson’s ratio arrives to its limit ( ɛ ≈ 0.4) for the isotropy of the used material. This way it is not possible to increase the reliability index value when using the Performance-Based IOSF Approach.

As result, it is very important to use both alternative approaches when dealing with this kind of problems during the conceptual design stage in order to open more categories of solutions as layouts for the detailed design stage. Thus, RBTO using the developed approaches is able to generate two groups of solutions, providing the designer with a range of topologies.