Reliability evaluation and analysis of interconnection network using edge-disjoint minimal path method

Published Online October 2018 in MECS DOI: 10.5815/ijcnis.2018.10.02

With the recent advances in technology the design of robust interconnection network is always a challenging issue. Interconnection network (IN) plays an important role in the design of large scale and complex real time systems, as it provides the basic mean of data exchange among different components of such networks. Communication networks, multistage interconnection networks, stochastic flow networks, distributed network are some examples of real time systems. The operationability of such systems largely depend on the robustness of their interconnection networks. Thus, in general, it is quite apparent that interconnection network must be operational to ensure a robust system as a whole. Reliability is a parameter that measure successful operation of interconnection network. Out of many reliability measure network reliability is an important measure as it ensures at least one operational path among each node to every other node.

The exact evaluation of network reliability of interconnection network is found to be NP-hard [1]. The existing methods to evaluate the network reliability of interconnection network are mainly based on sum of disjoint product method [3, 4, 11], enumeration of path sets/cut sets or spanning trees [5, 10, 11, 14, 15, 16], binary decision diagram(BDD) [7, 8, 12], factoring theorem [6], multiple variable inversion [9], etc. A detail discussion on these methods can be found in [15]. The worked carried out in [15] provides a clear insight into the use of cut-sets to evaluate the different reliability measures. Further, the difficulty in the use of path sets/spanning trees to evaluate the reliability is also discussed in this paper. In order to minimize the number of path sets, edge disjoint minimal path sets can be used as a substitute. Two minimal paths are said to be edge disjoint if they have no edge in common. Thus, k-disjoint minimal path problem can be defined as there must exist disjoint paths among k distinct pair of vertices such that every path connects a source node to a destination node pair[16].It is further found that this problem is NP-complete even for K=2 [16].

The work carried out in this paper involves generation of edge disjoint pathsets among every pair of nodes. The connectivity among all the nodes is ensured by merging all disjoint minimal paths from each source node to rest of the nodes such that it does not form any cycle. Thus, a number of spanning tree rooted on that each nodes of the network are generated. The reliability is then evaluated by applying sum-of-disjoint technique on these spanning trees.The rest of the paper is organised as follow: Proposed method is presented in Section II, Section III illustrates the proposed method in step wise manner by taking a suitable example, Section IV comprises of the simulated results and discussions and Section V concludes the paper with its future scope.

• II.    Proposed Method

The steps followed in the proposed method are as follows:

• 1.    It generates all edge-disjoint minimal paths between every pair of nodes of the interconnection network.

• 2.    The second step involves merging of the edge disjoint minimal paths from each source nodes to the rest of nodes occurs only if such merging of minimal paths does not result into cycle.

• 3.    Step 2 ensures connectivity of all nodes of interconnection network without any cycle which is equivalent to the generation of spanning trees.

• 4.    Step 1to 3 can be repeated to generate a number of spanning tree rooted on each source node are generated and ranked according to their generation.

• 5.    The network reliability is then evaluated from these spanning trees by applying sum of disjoint product techniques on these trees.

The following Notations and assumption are used for the rest of the paper

NOTATIONS

G        G is the probabilistic graph of IN

N       number of nodes

• L        number of links

p          link reliability

A        adjacency matrix of G

D       degree of a node with minimum connectivity

NR      network reliability

P       minimal path

d(v)      degree of the node v

D        degree of the node with minimal connectivity

• s,    t       source and destination nodes

Path_set set of MPs from one source node to rest of the nodes of G

Assumption:

• i)    The nodes are assumed to be perfectly reliable.

• ii)    The failure of the link are statistically

independent with known probability.

Theorem: An upper bound to number of edge disjoint minimal paths(K) between any pair of nodes s and t = minimum {d(s), d(t)}

Proof: The connectivity of a node v is a function of its degree i.e. d(v). Thus, the node v gets disconnected if its d(v) number of edges fail. Hence, an upper bound to the number of edge disjoint paths that which can be generated from/to this node is d(v). If v=s, d(s) is the maximum number of edge disjoint paths can be generated from it to other nodes and likewise d(t) is the maximum number of edge disjoint paths that can generated from other nodes to t when v=t. If d(s) > d(t) and let the number of minimal paths between s and t be d(s). The number of edge disjoint paths between s and t must be < d(t) (as d(t)

Lemma : An upper bound to the number of edge disjoint paths generated between any pair of nodes of an interconnection network is the degree of the node with minimal connectivity.

Proof : The proof to this lemma is straightforward from theorem 1 and the definition of edge disjoint paths.

If two minimal paths are said to be edge disjoint if they have no edge in common.

The proposed method first generates all the edge disjoint minimal path between every pair of nodes. The minimal paths thus generated are ranked into K number of categories.

K=1This is the main minimal path set between every pair of nodes.

• K=2    This is the first spare minimal path set (i.e if the main minimal path fails)

K=3This is the second spare path set between every pair of nodes. It comes to be operational when main and first spare minimal path set fails and so on.

The path sets belonging to each rank are merged if the following condition holds:

• i)    The merge operation does not form cycle ii) The path set to be merged must be unique

After successful merging of all the pathsets, the resulting path set ensures connection of every nodes to other nodes without cycle which is equivalent to the generation of spanning tree. Thus K number of such path sets are generated. The network reliability Can be calculated using SDP method [3 ].

• A.    Proposed Algorithm to compute the Network Reliability of Interconnection Network

[NR]= Network_Rel_Eval(G, N, L, p)

A=adjacency matrix (G)

T=A % %% Temporary storage of A

D= fori=1 to N for j=1to N k=1 %%% first generated minimal path between i and j if(i * j)

P(i,j)k=generate a path between nodes i and j

T=(i,P(i,j) k (2))=0 %%% link is made as failed by setting it to a value 0

T=(P(i,j) k (2),i)=0 %%% as graph is undirected (for directed graph this line is not required)

k=k+1

while(True)

P(i,j)k=Generate_Minimal_Path(i,j) if(P(i,j)k=NULL) break else

T(i,P(i,j)k (2))=0 T(P(i.j)k(2),i)=0 end if end while end if end for end for i=1

k=1

Path_Set(i,k)= Null %%% Path_set is initialized to null for k=1to D fori=1to N forj=1to N iKi * j)

if cycle(Path_Set(i,k)U P(i,j) k )=false %%% checking whether the MP to be added results into cycle

Path_set(i,k)=Path_Set(i,k)UP(i,j)k} end if end for %%%Path_set contains all edge disjoint paths from node i to rest of the nodes representing the end for %%% spanning tree rooted on node i end for

%%%% Network reliability evaluation from the Path_set i=1

k=1

Rel=p\Path-Set(L 11 -p PathSt"'^- (1-p) %%%Path_set for first node is treated differently for k= 1 to D fori=2 to N

RK=plPalh-Sel(‘M x (i-p)^k %%% rest paths are treated as spare paths end for

Rel=Rel+Rk end for

• B.    Complexity of the Proposed Algorithm

The complexity of the proposed algorithm is presented below:

The proposed algorithm involves generation of all edge disjoint minimal path between every pair of nodes which takes a time of O(N2). The merging operation requires a worst case time complexity of O (DxN) which is less than O(N2). Hence the running time of the proposed algorithm is found to be O(N2).

• III.    Illustration

The proposed method is illustrated by taking the following example:

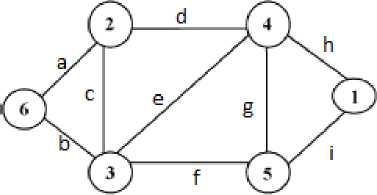
Fig.1. An Example Network with 6 Number of Nodes and 9 Number of Links

The example network has 6 numbers of nodes and 9 number of links. The algorithm first generates all minimal paths between node 1 to the rest of the node. The step is repeated for each node as a source node. Thus, 12 number path sets are generated for the said network (Table1). For each case, two such paths are possible which are labelled as K=1 and =2.The merging operation is performed on paths that belong to same label e.g. for node 1 {a, d, h, e, i} is generated for K=1. The results of such merging operation are the trees.

The generation of the minimal path set from first node i.e. 1 to rest of the nodes is explained below:

Path_set(1,1) = Null

Path_set (1,1)

= Path_set (1,1)

и [d, h} since cycle( Path_set (1,1) и [d, h})

= false

Path_set (1,1) = Path_set (1,1) и {e, h}

= {d, h, e} since cycle( Path_set (1,1) и {e, h})

= false

Path_set (1,1) = Path_set (1,1) и {h} =

{d, h, e} since cycle( Path_set (1,1) и {i}) = fasle

Path_set (1,1) = Path_set (1,1) и {i} =

{d,h,e,i} since cycle( Path_set (1,1) и {i}) = fasle

Path_set (1,1) = Path_set (1,1) и {a, d, h} = {a,d,h,e,i} since cycle( Path_set (1,1) и {i}) = fasle

Table 1. Edge Disjoint Minimal Paths between Every Pair of Nodes

K	Edge disjoint minimal paths					Path_set( i, k)
	P(1,2)	P(1,3)	P(1,4)	P(1,5)	P(1,6)	i=1
K=1	{d, h}	{e, h}	{h}	{i}	{a, d, h}	{a, d, h, e, i}
K=2	{c, f, i}	{f, i}	{g, i}	{g, h}	{b, f, i}	{b, c, f, i, g}
	P(2,1)	P(2,3)	P(2,4)	P(2,5)	P(2,6)	i=2
K=1	{d, h}	{c}	{d}	{c, f}	{a}	{d, h, c, f, a}
K=2	{c, f, i}	{d, e}	{c, e}	{d, g}	{b, c}	{c, f, i, e, b}
	P(3,1)	P(3, 2)	P(3, 4)	P(3, 5)	P(3, 6)	i=3
K=1	{e, h}	{c}	{e}	{f}	{b}	{e, h, c, f, b}
K=2	{f, i}	{d, e}	{c, d}	{e, g}	{a, d, e}	{f, i, d, e, a}
	P(4,1)	P(4, 2)	P(4, 3)	P(4, 5)	P(4, 6)	i=4
K=1	{h}	{d}	{e}	{g}	{e, b}	{d, h, e, b, g}
K=2	{g, i}	{c, e}	{g, f}	{h, i}	{d, a}	{g, i, e, c, a}
	P(5, 1)	P(5, 2)	P(5, 3)	P(5, 4)	P(5, 6)	i=5
K=1	{i}	{g, d}	{f}	{g}	{f, b}	{i, g, d, f, b}
K=2	{g, h}	{f, c}	{g, e}	{h, i}	{g,d, a}	{a, d, h, b, f}
	P(6,1)	P(6, 2)	P(6, 2)	P(6, 4)	P(6, 5)	i=6
K=1	{b, f, i}	{a}	{b}	{a, d}	{b, f}	{b, f, i, a, d}
K=2	{a, d, h}	{b, c}	{a, c}	{b, e}	{a, d, g}	{a, d, h, c, g}

All the path_set generated each representing a unique spanning tree are presented in Table -2

Pel = p⁵ + 6 x (1 - p) x p⁵ + 5 x (1 - p)² x p⁵

Considering the link reliability as 0.9, the network reliability is found to 0.9735 i.e.

Pel = 0.9735 (for p = 0.9)

Table 2. Generation of Spanning Trees using the Proposed Algorithm

Sl. no	Path set (spanning tree)	Spanning trees in disjoint form	Rank
1	{a,d,h,e,i}	{a,d,h,e,i}	1
2	{b, c, f, i, g}	{ e, b, c, f, i, g}	2
3	{d, h, c, f, a}	{Г, a, c, d, h, f}	1
4	{c, f, i, e, b}	{a, 7г, b, c, e, f, i,}	2
5	{e, h, c, f, b}	{ a, b, c, e, f, h,}	1
6	{f, i, d, e, a}	{ 6,h, a, d, e, f, i}	2
7	{d,h, e, b, g}	{a, b, d, e, g, h}	1
8	{g, i, e, c, a}	{b, d, a, c, e, g, i}	2
9	{i, g, d, f, b}	{e, b, d, f, g, i}	1
10	{a, d, h, b, f}	{g, a, a, b, d, f, h}	2
11	{b, f, i, a, d}	{ h, a, b, d, f, i}	1
12	{a, d, h, c, g}	{ f,e a, d, h, c, g}	2

• IV.    Results and Discussion

• A.    Comparison and Validation of the Proposed Method

In order to ensure the correctness of the proposed method, the network reliability computed by the proposed method is validated against the standard method [15] for the set of benchmark networks. The validated results along with the no. of spanning trees used are presented in the table 1. From this table, it is quite apparent that the proposed method is able to evaluate the network reliability of the said network with a tolerable discrepancy while using very less no. of spanning trees in comparison to all possible spanning trees.

• B.    Network Reliability Evaluation of Regular Interconnection Network

The proposed method is applied on different types of interconnection network viz. Regular network, Irregular network, communication network etc.

Table 3. Validation of the Proposed Method against Method [15]

Sl. No	Network	Network reliability Computed by method [15 ]	Network reliability Computed by Proposed method	Number of spanning trees		% of error
				Used by Proposed method	Maximum Possible no.
1	6N9L	0.9932	0.9749	18	81	1.83
2	7N10L	0.9722	0.9275	14	96	4.47
3.	8N11L	0.9696	0.9360	16	168	3.36
4.	8N12L	0.9711	0.9412	18	247	2.99
5.	8N13L	0.9919	0.9742	20	576	1.77
6.	9N14L	0.9701	0.9288	18	647	4.13

The interconnection network of interest under this case are hypercube(HC)[17] and its variation like Twisted hypercube(THC),    crossed cube(CC), Varietal hypercube(VHC), fault tolerant hypercube(FTHC), 3-D Torus and 3-D mesh, Fault tolerant Hypercube, Folded Hypercube etc.

The value of network reliability evaluated along with the path set for this type of interconnection network are presented in table-4 by varying input link reliability from 0.1 to 0.9. From this table the following facts can be observed.

• i)    The mesh network with a reliability of 0.59 is highly unreliable among the aforesaid network

• ii)    CC, VHC, THC are found to have the same value of network reliability which is greater than the network reliability of hypercube .This may be due to the reason that all those variation have the same number of nodes and links with different layout. The folded hypercube with four more number of links provide more reliability value than its variation discussed earlier.

• iii)    2-D Torus with 16 nodes provides better reliability values than hypercube due to higher degree of connectivity among communicating nodes.

Time dependent reliability analysis of the said interconnection network is performed by plotting their network reliability against the mission time (t) in hours under link failure rate, where link failure rate (Л) can be define as follows:

p(t) = exp ^Zt. The link failure rate is set to a value of 0.01.

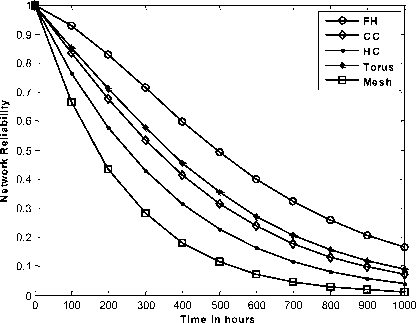
Fig.2. Comparison of Network Reliability of some Regular IN under Link Failure Rate

Table 4. Network Reliability Computed by the Proposed Method for some Regular IN

Sl. No.	p	HC	VH	CC	THC	FTH	FH	Mesh	Torus
1	0.1	0.0192	0.0279	0.0279	0.0279	0.1244	0.1244	0.0000	0.1017
2	0.2	0.0737	0.1032	0.1032	0.1032	0.2781	0.2781	0.0003	0.2120
3	0.3	0.1584	0.2136	0.2136	0.2136	0.4380	0.4380	0.0024	0.3343
4	0.4	0.2680	0.3467	0.3467	0.3467	0.5882	0.5882	0.0102	0.4667
5	0.5	0.3967	0.4907	0.4907	0.4907	0.7188	0.7188	0.0313	0.6033
6	0.6	0.5379	0.6341	0.6341	0.6341	0.8246	0.8246	0.0778	0.7344
7	0.7	0.6841	0.7656	0.7656	0.7656	0.9043	0.9043	0.1681	0.8480
8	0.8	0.8256	0.8750	0.8750	0.8750	0.9587	0.9587	0.3277	0.9320
9	0.9	0.9478	0.9537	0.9537	0.9537	0.9899	0.9899	0.5905	0.9780

Table 5. Network Reliability of fully Connected IN

Sl. No.	G(N,L)	No. of spanning trees		Total no. of edge Disjoint Paths generated from each node to the rest of nodes	Network reliability	CPU time to generate all possible spanning trees	CPU time required by proposed method
		maximum possible	used by proposed method
1	G(3,3)	3	3	12	0.99	0.0109	0.012
2	G(4,6)	16	12	36	0.99	0.1147	0.022
3	G(5,10)	125	20	80	0.99	0.7489	0.0495
4	G(6,15)	1296	30	150	0.99	56.5741	0.0895
5	G(7, 21)	16807	42	252	0.99	121.6098	0.1580
6	G(8, 28)	262144	56	392	0.99	364.1097	0.1872
7	G(9, 36)	4782969	72	576	0.99	710.8720	0.2458
8	G(10, 45)	100000000	90	810	0.99	10761.9651	0.3408

The Time dependent analysis (Fig.2) of said IN reveals observations similar to Table-4. The network reliability of FH is found to be around 0.6 even after 500 working hours while this value decreases to below 0.2 during 1000 working hours. The network reliability of other INs after 500 working hours are 0.4 (for Torus), 0.35(for CC), 0.25(for HC) and 0.15 (for Mesh) while those of these INs are below 0.1. Hence, FH is considered to be the mostsuitable interconnection network in terms of the reliability point of view.

• C.    Network Reliability Evaluation of Fully Connected Network

The network reliability of fully connected network with nodes varying from 3 to 10 is calculated and presented in Table. The maximum possible no. of spanning trees that can be generated along with the time required to generate them are presented in 3rd and 7th column of this table. Column 4 shows thetotal no. of edge disjoint paths generated from each node to the rest of the nodes. From this table, it can be observed that the no. of spanning trees used by the proposed method is very less in contrast to the actual required which saves CPU time to a greater extend.

• V.    Conclusion

This paper proposes a new method to compute the network reliability of interconnection networks considering very less number of spanning trees. The simulated results obtained from the proposed method are validated against an existing method of same interest. This has been observed from this validation that the proposed method estimates the network reliability of a set of bench mark networks with a maximum of 5% of error while considering very less number of spanning trees in reliability evaluation. The reliability of some regular interconnection networks viz, hypercube, crossed cube, folded hypercube, mesh and torus have been evaluated and analysed. Folded hypercube provides a very high reliability value while mesh provides the least reliability values under same working environment. Network reliability of full connected networks are evaluated varying size from 6 to 10. The results show that there is remarkable saving of CPU time to compute the network reliability of these networks in contrast to the actual no. of spanning trees required. The work carried out in this paper can be extended further to evaluate network reliability of very large sized networks with nodes having different connectivity.