Рентгенографическое исследование дефектов упаковки и двойников в сплавах железа и цементите Fe3C

Дефекты упаковки (ДУ) играют исключительно важную роль в процессах фазовых переходов, двойникования, пластической деформации [1, 2]. Они обычно возникают [1, 2] как следствие расщепления полных дислокаций, релаксации внутренних напряжений при мартенситных превращениях либо воздействия внешних напряжений. Наиболее важными реакциями расщепления являются

1 a < 110 >^ 1 a < 121 >+ 1 a < 211 > в плоскостях { 1 11 } ГЦК-решётки и

1 a < 111 >> 1 a < 111 >+1 a < 111 > в плоскостях {112 } ОЦК-решётки. Расщеплённая дислокация имеет вид ленты дефекта упаковки, окаймлённой частичными дислокациями. Ширина дефекта 5 определяется энергией дефекта упаковки у:

_ Gb 2 2 -уГ, 2 v       ) 1

5 =--1 1-- cos2 B I-,

8 п 1 - v (    2 - v J y

где v - коэффициент Пуассона; b - модуль вектора Бюргерса полной дислокации; р - угол между линией полной дислокации и её вектором Бюргерса [1]. Энергия ДУ в ГЦК-металлах определяется разностью свободных энергий ГЦК- и ГПУ-фаз, а в сплавах очень сильно зависит от электронной структуры [1, 2].

Особенности дифракции рентгеновских лучей на дефектах упаковки, позволяющие определять их концентрацию, рассматривают в рамках слож- ных теорий даже для простейших ГЦК- и ОЦК-структур [2, 3]. Но в данной статье предложен и используется простой геометрический метод анализа картины дифракции в материале с произвольной атомной структурой, содержащем дефекты упаковки.

Определение концентрации дефектов упаковки. В рентгенографии [2, 3] для учёта количества ДУ вводят вероятность образования дефекта упаковки а . Этой величине можно придать смысл доли дефектных плоскостей, если дефект упаковки охватывает всю атомную плоскость. В случае лент дефектов упаковки под а следует понимать отношение площади всех лент ДУ к площади всех плоскостей решётки в том же объёме.

Из рис. 1 ясно видна причина, по которой ДУ влияют на дифракцию рентгеновских лучей: в том месте 1 – 2 , где падающий луч пересекает плоскость дефекта упаковки, фактическое межплоскостное расстояние для отражающих плоскостей оказывается бóльшим (или меньшим), чем в бездефектных участках. Изменение межплоскостного расстояния * — d

A d = ^ о •- = ^ o cos ф ,                       ⁽³⁾

d где с0 - вектор сдвига при образовании ДУ; d -вектор, перпендикулярный к отражающей плоскости и равный по модулю межплоскостному расстоянию d; ф - угол между векторами с0 и d .

Металловедение и термическая обработка

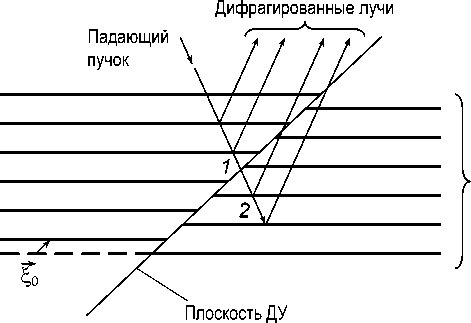
Отражающие плоскости

Рис. 1. Объяснение причины влияния ДУ на дифракцию рентгеновских лучей

Таблица 1

Значения параметра K _hkl некоторых плоскостей ГЦК-решётки

Отражение { hkl }	111	200	220	311	222
K hkl	–0,0345	+0,0689	–0,0345	+0,0125	+0,0172
Отражение { hkl }	400	331	420	422
K hkl	–0,0345	–0,0073	+0,0069	0

Из уравнения Вульфа – Брэггов следует, что

• = - ctg θ ⋅ Δθ , то есть происходит некоторое d

изменение угла отражения θ падающего луча от плоскости ( hkl ) по сравнению с бездефектным состоянием. Поскольку ДУ возникают с вероятностью α , то изменение угла отражения составит

Δθ=-α ^{ξ 0cos ϕ} tg θ .                     (4)

d

Для кристаллов кубической сингонии sinθ = λ-VH2+K2+L2 ,                (5)

2a где H = nh, K = nk, L = nl – индексы интерференции, пропорциональные индексам отражающей плоскости (hkl), n – порядок отражения, a – параметр решётки, а λ – длина волны рентгеновского излучения.

Уравнение (4) абсолютно точно для монокристаллов. В том случае, когда исследование проводят на поликристаллических образцах, в уравнении (4) следует провести усреднение cos ϕ по всем плоскостям, входящим в состав данного семейства { hkl }, и тогда (в градусах) результирующее смещение равно

360°

Δ (2 θ ) =- 360 K hkl α tg θ ,                  (6)

π

ξ1

где K_hkl = ξ ⁰ ⋅ ∑ cos ϕ _i ; p – фактор повторяемо- d p_i

a сти; d =             – межплоскостное расстоя-

• V h ² + k ² + l ²

ние. Значения Khkl некоторых плоскостей для ГЦК-решётки приведены в табл. 1. Видно, что смеще- ние дифракционных максимумов для различных плоскостей неодинаково как по величине, так и по знаку. Это обстоятельство используют при экспериментальном определении α [2].

Уширение дифракционных максимумов дефектами упаковки. Широко распространено мнение, что ДУ вызывают уширение дифракционных линий. Такое мнение абсолютно ошибочно. Если бы ДУ располагались строго периодически, то никакого уширения бы не было. Это понятно: периодическое расположение дефектов упаковки фактически создаёт новый кристаллографический тип структуры. Уширение же линий обусловлено отклонениями расположения ДУ от периодического.

Уоррен [2] рассмотрел предельный случай, когда расположение ДУ было совершенно хаотическим. Оказалось, что такая система ДУ вызывает уширение, аналогичное (в смысле угловой зависимости) уширению от дисперсных блоков. Это означает, что при работе стандартными методиками (гармонический анализ, метод интегральной ширины линий) измеряется не размер истинных блоков, а некоторая комбинированная величина, которую обозначают как эффективный размер блоков, причём

1 ₌ 1 ₊ 1,5 α _V п п        V hkl ,

D _эфф   D a

где D – истинный размер блоков, а числовые значения параметра V hkl равны (для ГЦК-структуры):

Отражение hkl	111	200	220	311	222	400
V hkl	3	1	2	3 11	3	1
	4		2	22	4

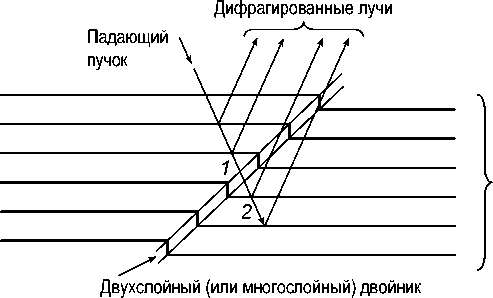
Отражающие плоскости

Рис. 2. Дифракция рентгеновских лучей около двойника

Как видно из (7), при наличии ДУ уширение максимумов дифракции, а следовательно, и измеряемый размер блоков D _э фф оказываются анизотропными. Максимальное уширение должно наблюдаться для рефлекса 200. Однако анализ уширения часто не проводят, вероятно, потому, что значения а (полученные решением системы уравнений (7) для отражений 111 и 200 и по смещению пиков) не очень хорошо согласуются. Это понятно: смещение пиков определяется числом всех дефектов упаковки, а уширение – только хаотических.

Двойниковые дефекты в ГЦК-структуре. Уоррен [2] рассматривал также двойниковые дефекты по плоскостям {111} ГЦК-кристаллов типа ABCACBA, которые, по существу, являются двухслойными двойниками. С точки зрения теории дифракции, между дефектом упаковки и двойниковым дефектом нет большой разницы. И в этом случае фактическое межплоскостное расстояние для падающего луча на интервале 1–2 около двойника (рис. 2) окажется больше, чем в бездефектных участках кристалла. Следовательно, результат дифракции от двойника и дефекта упаковки должен быть похожим. Так и было бы, если бы в ГЦК- кристаллах не существовало двух взаимно противоположных и равновероятных направлений двой- никования, в силу чего суммарное смещение пиков отсутствует. Уширение, конечно, имеется, если двойниковые дефекты расположены хаотиче- ски. Если Р - вероятность обнаружить двойниковый дефект, то выражение для Dэфф усложняется:

^D эфф

—--+

D

1,5а + РТЛ

V hkl , a

где значения Vhkl те же, что и в (7). Кроме уширения линий двойниковые дефекты создают асимметрию их формы. Но её изучение требует особо точной методики фиксирования интенсивности и проводится редко.

Дефекты упаковки и двойники в ОЦК-металлах. Обычно ограничиваются рассмотрением ДУ и двойниковых дефектов по плоскостям { 112 }. Каждая из них является плоскостью и скольжения, и двойникования. Образование дефекта упаковки по ней может происходить смещением атомов на вектор ^0, равный либо 6 a[111], либо - 6 a[111]. Если оба варианта равновероятны, то смещение пиков отсутствует. По существу, главный способ измерения концентрации ДУ и двойников в ОЦК-структуре состоит в анализе анизотропии уширения [4]. Точно так же, как и для ГЦК-структуры, можно ввести эффективный размер блоков. Оказывается, что для ОЦК

1      1 , а + (2/3)рТЛ м '                 V hkl ,

D эфф   D     a

где значения V_hkl для различных отражений равны:

Отражение hkl	110	200	211	220	310	222
V hkl	0,71	2,0	1,22	0,71	1,90	1,73

Изучение двойникования в железоникелевых сплавах. Методикой гармонического анализа формы линий с использованием компьютерных расчётов были измерены эффективные размеры блоков а -мартенсита большой группы сплавов Fe–Ni, закалённых от 1050 °C в воде, а затем в жидком азоте. Методика эксперимента была такой же, как в [4]. Результаты представлены в табл. 2. По существу, в последней колонке табл. 2 стоит вероятность образования двойниковых дефектов р , так как электронная микроскопия не обнаруживает дефектов упаковки. Интересно, что: 1) микродвойники присутствуют во всех сплавах; 2) основное уширение дифракционных максимумов мартенсита создают двойники.

Легко показать, что если f – объёмная доля двойников, а t – их толщина, то

Р — 2d^ f , (10) где d 112 – расстояние между соседними плоскостями {112}. Для сплава Fe–33 % Ni из выражения (10) следует, что при f =0,5 толщина микродвойников t =25 Å, что совпадает с данными электронной микроскопии.

Металловедение и термическая обработка

Таблица 2

Характеристики структуры сплавов Fe–Ni

Сплав	Эффективные размеры блоков, Å			Истинный размер блоков, Å	(1,5 а + вр103
	110 D эфф	100 D эфф	211 D эфф
Fe–10 % Ni	680	360	720	1300	4,3
Fe–15 % Ni	420	205	270	950	8,1
Fe–17 % Ni	350	160	220	950	11
Fe–20 % Ni	280	130	200	750	13,5
Fe–25 % Ni	210	95	140	590	18
Fe–27 % Ni	200	90	140	600	18,5
Fe–30 % Ni	180	75	145	750	25,3
Fe–32 % Ni	150	56	100	1000	34,2
Fe–33 % Ni	140	50	100	5400	42,1
Fe–25 % Ni	210	95	140	590	18
Fe–25 % Ni–1,5 % Mn	185	85	130	520	21
Fe–25 % Ni–3 % Mn	170	80	100	460	23

Изучение дефектов упаковки в цементите. Дефекты упаковки в цементите по плоскости (001) наблюдались неоднократно [ 5-7 ] . Молекулярнодинамические расчёты показывают, что энергия ДУ в этой плоскости является минимальной [8]. Детально вопрос о кристаллогеометрии образования ДУ в литературе не рассматривается, но, на наш взгляд, можно предложить следующую модель. Любой ДУ может быть получен путём сдвига части кристалла на нетрансляционный вектор. Решётка цементита образована чередующимися вдоль [ 001 ] слоями призм типа А и В (...АВАВАВ...); наименьшее расстояние между атомами железа двух соседних слоёв призм равно 2,49 Å. Среди всех возможных вариантов сдвига по (001) минимальное изменение межатомных расстояний обеспечивает сдвиг вдоль [ 010 ] слоя А относительно слоя В на 0,390 параметра решётки a ₂ или, соответственно, слоя В относительно слоя А на

–0,390 a ₂ (рис. 3). При таком сдвиге кратчайшее расстояние Fe–Fe немного уменьшается (до 2,19 Å), что, по-видимому, потребует небольших локальных смещений атомов железа, но расстояния Fe– C не изменяются. Отметим, что близкие величины сдвига были получены в эксперименте [7] (< 0,5 a ₂) и при моделировании методом молекулярной динамики [8] (0,40...0,44 a 2 ).

Экспериментальное исследование было проведено на образцах углеродистой стали с 1,53 % С. Плоские образцы толщиной 2 мм аустенитизировали в соляной ванне при 1050 °С и переносили в ванну для распада у -фазы, где выдерживали 2,5 ч при 330 °С и 1 мин при 500 °С для получения перлита различной дисперсности.

Запись профилей интенсивностей дифракции проводилась на дифрактометре STADI-P в моно-хроматизированном Cu K _а излучении в режиме сканирования с шагом 0,030° по углу 2 9 . Дифрак-

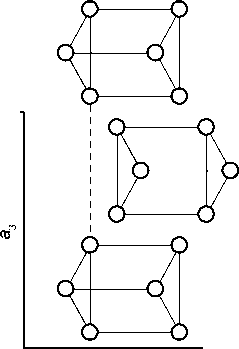
а)

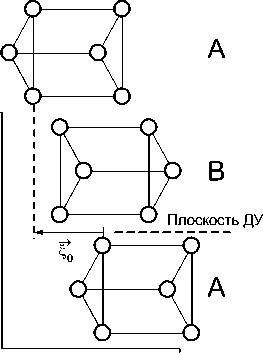
б)

a2

a2

Рис. 3. Проекция решётки цементита вдоль направления [100]: а – бездефектная решётка;

^*

б - решётка с дефектом упаковки § 0 = - 0,390 а ₂ в плоскости (001)

Таблица 3

Значения параметров p и G HKL в теории уширения от дефектов упаковки ^ 0 = 0,39 а ₂

в плоскости (001) цементита

d HKL , Å	HKL	p	G HKL
2,38	112 и 021	0,435	1,54
1,76	212	0,585	1,85
1,68	004 и 023	0,681	0,61
1,59	130	0,146	0

тограмма каждого образца была записана в интервале углов 2 9 от 16 до 68°, что соответствует межплоскостным расстояниям от 5,54 до 1,38 Å. К сожалению, многие максимумы цементита перекрываются друг с другом либо с линиями феррита, поэтому фактически удалось использовать только четыре максимума. Соответствующие им межплоскостные расстояния и индексы интерференции указаны в табл. 3. Ширина линий определялась по методу интегральной ширины; физическое уширение выделялось по формуле р = 4b ² - b 2 , где b -

Вторым источником уширения дифракционных линий являются поля упругих искажений, создаваемых дислокациями или возникающих в ходе фазовых превращений из-за объёмных изменений [ 13, 14 ] . Усреднённой характеристикой этих полей является 4 < £ ² >  - среднеквадратическая деформация в направлении нормали к отражающей плоскости, а эффект уширения выражается формулой [ 14 ]

р2 = 72Пtg9^V<£2 > . (14)

измеренная ширина максимума у исследуемого образца, а b _э - у эталона [ 9 ] . За эталонный, то есть не дающий физического уширения, был принят образец, который после распада у -фазы при 500 °С был отожжён в течение 20 ч при 700 °С. По сравнению с ним у остальных двух образцов максимумы интенсивности дифракции были уширены.

Рассмотрим основные причины уширения. Эффект уширения от дефектов упаковки можно рассчитать на основе метода [10] при использовании выражений (3) и (4) и формулы Селякова– Шеррера [9], связывающей угловое уширение максимума с размером блоков D :

в 1 ( 9 ) = . (11)

2 D cos 9

Будем считать, что уширения Р 1 и р ₂ складываются в квадратичной форме, то есть полное уширение максимумов р ² = Р 2 + Р 2 . Легко уви-

деть, что

4 р ² ■ cos² 9 X ²

I SЦ)

+ 8л- < £2

sin² 9

X2

Г =

+

I S Ц

G HKL а

a 3     )

+ 8л- < £2

> ■

sin² 9

X2

Цементит в перлитной структуре имеет форму пластин с плоскостями габитуса (101) или (001) [11, 12], поэтому величину D следует заменить на D эфф :

^D эфф

Р + G HKL

S _Ц     a ₃

а ,

График зависимости приведённого уширения 4 p ²cos² 9 / X ² от переменной 8 л sin² 9 / X ² должен выражаться прямой с наклоном, пропорциональным деформации <  £ ² >. На рис. 4 представлены такие зависимости для цементита перлита, образовавшегося при 330 и 500 °С. При построении графиков использованы указанные в табл. 3 четыре отражения, которые не сливаются с другими максимумами. Отметим, что для первых трёх максимумов дифракции фактор p последовательно воз-

где S Ц – средняя толщина цементитных пластин; p – усреднённый по всем возможным ориенти-

ровкам пластин цементита косинус угла между нормалями к отражающей плоскости и плоскости габитуса пластины; a 3 – период трансляции в направлении [001], перпендикулярном плоскости ДУ, а G_HKL – ориентационный фактор уширения дифракционных пиков дефектами упаковки:

G hkl = 4 d HKL" sin 2 (0,39 KL ).             (13)

a ₃

Численные значения p и G_HKL приведены в табл. 3.

растает, однако монотонно восходящих кривых не наблюдается. Графики имеют пилообразную форму, свидетельствующую об анизотропном уширении, которое обычно создают ДУ.

Следует обратить внимание, что минимальную ширину имеет отражение 130, на которое, согласно данным табл. 3, ДУ влияния не оказывают. Но если судить по ординатам на рис. 4 для этого отражения, то величина <  £ ² > должна быть пренебрежимо мала. Поэтому концентрацию ДУ и толщину пластин цементита рассчитывали как решение системы уравнений (15), записанных для разных отражающих плоскостей. Результаты такого расчёта по экспериментальным данным рис. 4 приведены в табл. 4. Степень согласия рассчитан-

Металловедение и термическая обработка

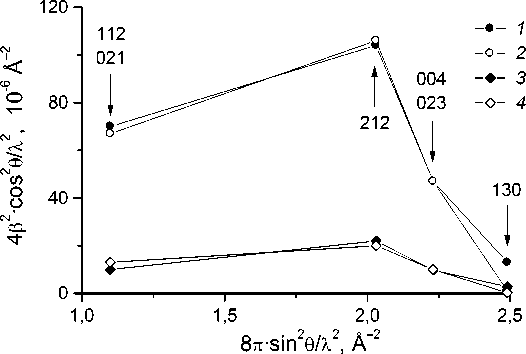
Рис. 4. Зависимости приведённой ширины дифракционных максимумов 4 β ² cos2 θ / λ ² от параметра 8 π sin2 θ / λ ² для перлита, образовавшегося при 330 °C ( 1 , 2 ) и 500 °C ( 3 , 4 ). 1 , 3 – экспериментальные данные;

2 , 4 – теоретический расчёт

Таблица 4

ного теоретического уширения с экспериментом показывают линии 2 и 4 на рис. 4.

Таким образом, разработанная методика рентгенодифракционного исследования дефектов упаковки в сплавах и соединениях железа по уширению последовательного ряда дифракционных максимумов позволяет надёжно определить концентрацию ДУ и её изменение в ходе различных структурных превращений.

Работа выполнена при поддержке Российского научного фонда (проект № 16-19-10252). В проведении экспериментальных исследований принимала участие А.Г. Тайзетдинова.