Рентгеноспектральные методы измерения степени упорядоченности углеродных наночастиц

В настоящее время одним из наиболее динамично развивающихся направлений в области нанотехнологий в строительстве является применение углеродных фуллероидных материалов (фуллерены,

фуллеренолы и их соединения, фуллероидные наночастицы) в качестве модификаторов свойств различных конструкционных материалов и пластификаторов бетонных смесей [1–4].

При производстве фуллероидных материалов методом дугового синтеза [5] продуктом синтеза явля-

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ ется углеродный порошок, в основном состоящий из аморфного углерода, представленного рыхлой глобулярной структурой. При этом полезные компоненты продукта синтеза фуллерены и фуллероид-ные наночастицы имеют упорядоченную структуру. При решении некоторых материаловедческих задач аморфный углерод не является мешающим компонентом, однако для применения смеси необходимо точно знать количественный состав аморфной фазы [6–8]. Кроме того, при отладке процесса синтеза необходимо оперативно контролировать количество выхода фуллероидных материалов, что представляет сложную аналитическую задачу.

В процессе синтеза фуллероидных материалов диссипативные пространственные и временные структуры, возникающие вдали от равновесия, образуют неравновесный порядок. В химических диссипативных системах возникший порядок состоит в проявлении колебаний и волн плотности вещества [9].

В процессах химического синтеза разрушение и возникновение каких-либо структур означает, что флуктуации, характерные для протекающей химической реакции, перестают играть роль «шума» и переходят в фактор создания упорядоченных продуктов реакции – появляется динамическая система, исследованию свойств которой посвящена данная работа.

Так как полезные компоненты синтеза представлены частицами, имеющими упорядоченную структуру, размещенными в аморфных углеродных глобулах, то целесообразно применить для исследований рентгеноструктурные и локальные рентгенофлуоресцентные методы исследований.

МЕТОДЫ И МАТЕРИАЛЫ

В настоящей работе применены следующие методы аналитического контроля: растровая микроскопия, локальный рентгеноспектральный анализ и рентгеновская дифрактометрия.

Проводились исследования продуктов синтеза фуллероидных материалов: образец С1÷С5 – образ- цы фуллеренсодержащей сажи, собранной на разном расстоянии от зоны дугового синтеза по методу, описанному в [10].

Аналитические измерения по определению структур, образованных в процессе синтеза, проведены с помощью приборов:

• 1.    Микроструктуру полученных образцов исследовали на сканирующем электронном микроскопе TESCAN VEGA 3SEM (Чехия).

• 2.    Спектры рентгеновской флуоресценции и элементный состав продуктов синтеза изучались с помощью Рентгенофлуоресцентной приставки PentaFET Precision (Oxford Instruments, GB) и пакета INCA, который позволяет определить элементный состав продуктов синтеза и их массовое количество. (Условия измерений: HV = 20.000e3, SpecimenCurrent = 681.611721612e-12, SpotSize = 272.683916892e-9). Расчет концентраций элементов, входящих в состав анализируемых продуктов, проведен методом фундаментальных параметров.

• 3.    Рентгенофазовый анализ продуктов синтеза выполнен с помощью дифрактометра D2 PHASER (Bruker, Germany).

РЕЗУЛЬТАТЫ

На рис. 1 приведены растровые изображения продуктов синтеза с различными увеличениями. Масштабный фактор на рис. 1, изображение a, составляет 60 мкм, для изображения b и c – 5 мкм. Изображение a – общая структура продуктов синтеза, изображения b и c – отдельные глобулы аморфного углерода и углеродные нанотрубки.

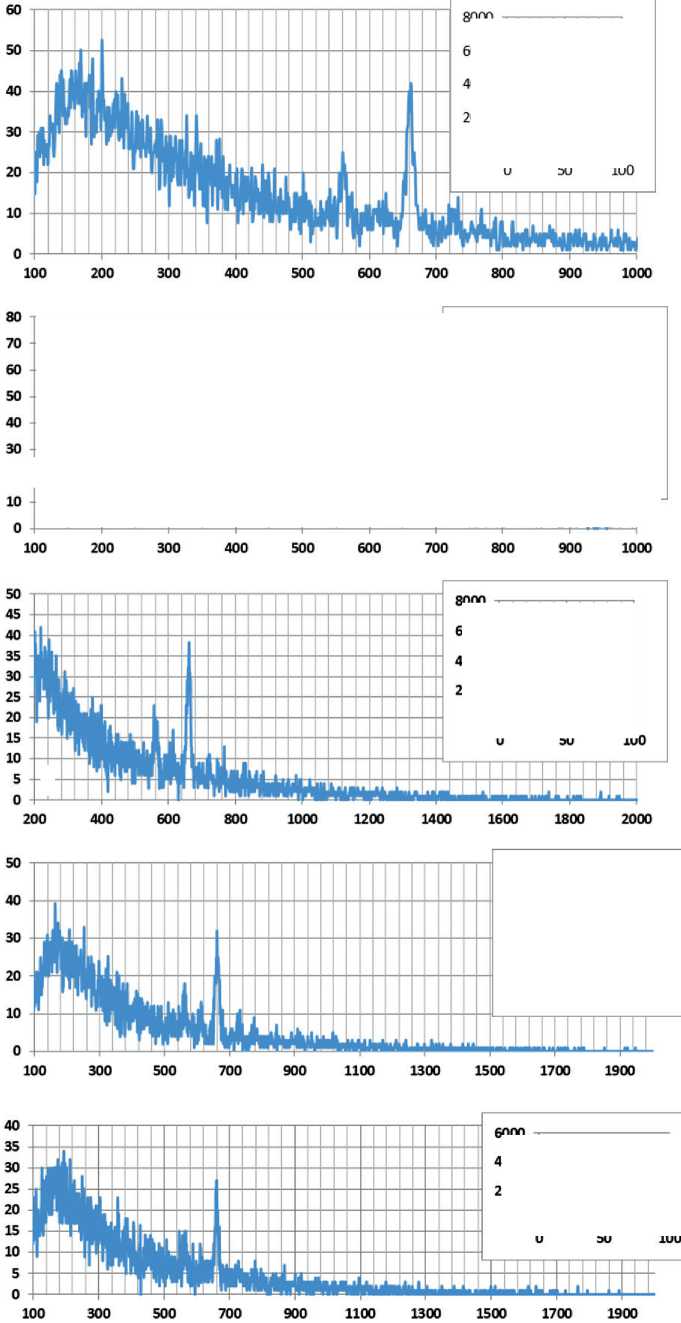
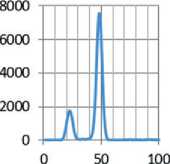
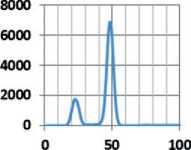
Спектры рентгеновской флуоресценции и элементный состав продуктов синтеза приведены на рис. 2 и в табл. 1.

На рис. 3 спектры продуктов приведены в сравнении, что позволяет провести сопоставление элементного состава для дальнейших преобразований.

Для выявления структуры проведен рентгенофазовый анализ продуктов синтеза, результаты которого

Рис. 1. Растровые изображения продуктов синтеза

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

Образец 1

Образец 2

Образец 3

Образец 4

Образец 5

—

8000

T-

6000

4000

I

1 "Л

Til

2000

ш

iul.

1/

0

■Uii^

ki£

3U

1UU

	A.
		Ю	100

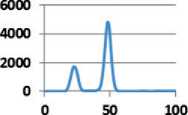
Рис. 2. Масштабированные по энергии рентгеновской флуоресценции спектры исследуемых образцов

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

Таблица 1

Результаты рентгенофлуоресцентного анализа

Образец	Концентрации обнаруженных элементов
	C	O	Si	Ni	Cr	Mn	Fe	Ni	Cu
C1	97,54	2,46	–	–	–	–	–	–	–
C2	96,93	1,67	–	–	0,26	–	1,14	–	–
C3	95,98	2,63	–	–	0,37	–	1,02	–	–
C4	80,54	6,81	0,27	1,11	1,42	0,41	6,83	0,99	7,62
C5	96,3	2,14	–	–	–	–	0,6	–	0,95

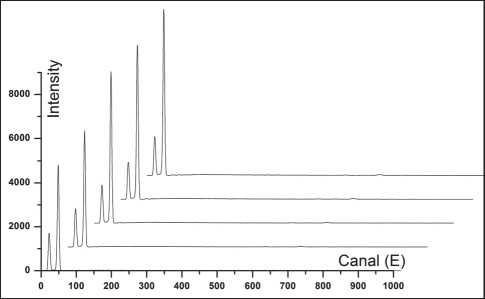
Рис. 3. Сравнение спектров рентгеновской флуоресценции образцов продуктов синтеза

приведены на рис. 4. Очевидно, что аморфные глобулы сильно влияют на формирование рентгеновского спектра и затрудняет фазовую идентификацию. В то же время анализ аморфной составляющей состава, которая является одним из продуктов выхода, позволит контролировать синтез на каждой стадии и при различных условиях его проведения.

ОБСУЖДЕНИЕ

Однозначного ответа структурные и флуоресцентные спектры по составу продуктов синтеза не дают. Это наглядно показано на рис. 2, 3 и 4. В то же время результаты исследований, приведенные в табл. 1, показывают на различие в элементном составе каждого образца, а рис. 4 указывает на наличие разных аморфных структур.

Процесс синтеза, образование продуктов различной структуры обладают свойствами нелинейных динамических систем, которые характеризуются вре- менной нелокальностью, немарково-стью, эредитарностью и эргодичностью

[11, 12]. Мерой самоподобия продуктов синтеза является показатель Херста, показывающий направление процесса образования аморфной и упорядоченной фазы [13].

Анализ нелинейной динамической системы

Нелинейную динамическую систему в полной мере характеризует аттрактор – компактное подмножество фазового пространства динамической системы, все траектории которой стремятся к нему при возрастании времени протекания процесса. Для динамических систем, обладающих нелинейными свойствами, аттрактор – это точка или множество точек (замкнутая кривая), к которым стремятся параметры состояния диссипативной системы, то есть аттрактор определяет конечное состояние диссипативной системы [12, 14].

Для построения аттрактора динамической системы необходимо рассчитать корреляционную размерность, размерность фазового пространства и фрактальную размерность исследуемого процесса. Корреляционная размерность и размерность фазового пространства рассчитывается по методу Такенса. Фрактальная раз-

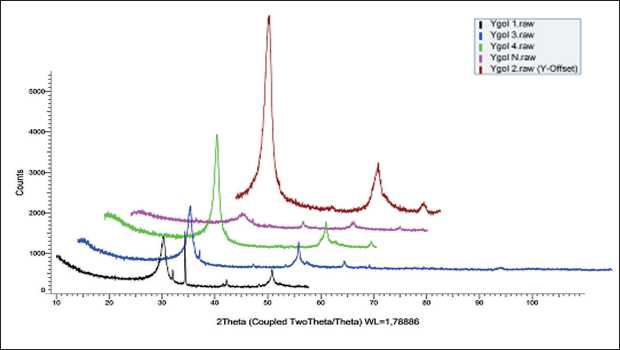
Рис. 4. Рентгеновские спектры продуктов синтеза

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ мерность вычисляется с помощью показателя Херста, который соответствует случайным процессам с независимыми приращениями [15], что характерно для систем химического синтеза.

Показатель Херста рассчитывается следующим образом:

R/S = (ατ) ^H , (1)

где α – постоянный коэффициент Херста, равный 1, τ – количество измеренных значений, R – размах отклонений числового ряда, S – стандартное отклонение числового ряда, H – показатель Херста.

Если показатель Херста H = 0,5, то приращения, характерные для процесса получения некоторых структур, не зависят от предыстории. Если выполняется неравенство 0,5 ≤ H < 1, то исследуемому процессу присуща долговременная «память». При 0 ≤ H <0,5 процесс характеризуется кратковременной «памятью». Если же H > 1, то имеет место суббаллистическое развитие процесса. То есть показатель Херста определяет меру персистентности – склонности процесса к трендам – затуханию, неустойчивому равновесию или к развитию [12]. Следует отметить, что фрактальная размерность аттрактора (фазового пространства) рассчитывается из показателя Херста как D = 2– H .

Основой для процедуры построения аттрактора является теорема Такенса для операций вложения множеств. По теореме Такенса почти для всех гладких динамических систем по измеренной реализации наблюдаемой динамической переменной можно сконструировать аттрактор, свойства которого будут идентичны исходной фазовой траектории. Для вычисления характеристик аттрактора необходимо иметь множество точек M , определенных в фазовом пространстве размерности n : M ≥ M_min = 10 ^{2+0 ,D} , где D – фрактальная размерность аттрактора [12, 14].

Для вычисления характеристик аттрактора реальной динамической системы, модель и размерность фазового пространства которой неизвестны, необходимо знать информацию о поведении динамической переменной. В нашем случае это изменение интенсивности вторичного рентгеновского излучения, зависящей от энергии флуоресценции и зависимость интенсивности рассеяния излучения рентгеновской трубки от угла Брегга.

Для экспериментальных данных размерность фазового пространства, как правило, неизвестна, при этом корреляционная размерность аттрактора Dcor сначала возрастает, затем выходит на постоянный уровень. Корреляционная размерность связана с размерностью фазового пространства следующим образом [14]:

n

^D^ - ^Dph + ^^-Lj, (2)

где ε = r/r_max – нормированный размах, σ – уровень шума (стандартное отклонение), erf (ε/2σ) – интеграл ошибок (табулированный).

Важное следствие аналитического результата состоит в том, что даже при ε = 3σ корреляционная размерность растет с увеличением размерности вложения.

В табл. 2 и на рис. 5 приведены результаты расчетов для рентгенофлуоресцентных спектров, полученные методом Таккенса и методом Херста.

В табл. 3 и на рис. 6 приведены результаты расчетов для структурных спектров, полученные методом Таккенса и методом Херста.

Аттракторы построены с помощью программы FRACTAN 4.4 по результатам измерений без предварительной обработки.

Сравнивая образы № 2 и 3, видно, что рассчитанный аттрактор и его размерные характеристики как для рентгенофлуоресцентного, так и для структурного спектра позволяют расширить информативность идентификации продуктов синтеза.

На рис. 7 показано сравнение исходных спектров флуоресцентного и структурного анализа и их 2D и 3D аттракторов, построенных по расчетам из табл. 2 и 3 соответственно.

Таблица 2

Размерные характеристики рентгенофлуоресцентных спектров

Образец	Корреляционная размерность	Размерность фазового пространства	Показатель Херста	Фрактальная размерность
Образец 1	1,68	6	0,65	1,34
Образец 2	1,61	4	0,66	1,33
Образец 3	0,34	1	0,62	1,38
Образец 4	0,33	1	0,62	1,37
Образец 5	0,36	1	0,63	1,37

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

№ 1

№ 2

№ 3

№ 4

№ 5

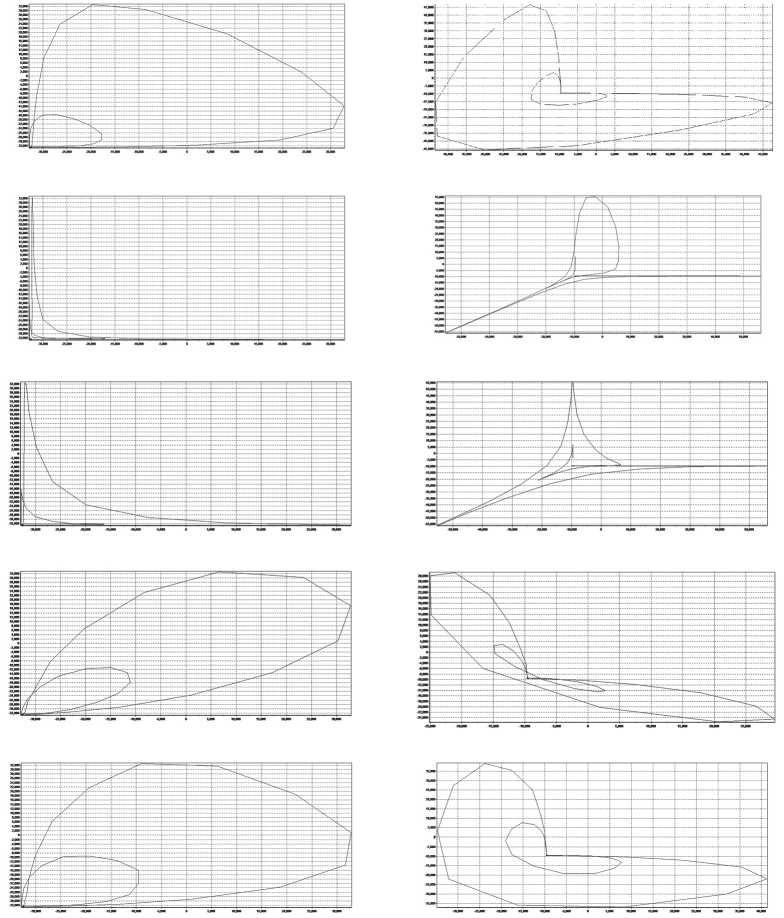
2D

3D

Рис. 5. Аттракторы образцов 1–5, построенные по результатам рентгенофлуоресцентных измерений

Таблица 3

Размерные характеристики структурных спектров

Образец	Корреляционная размерность	Размерность фазового пространства	Показатель Херста	Фрактальная размерность
Образец 1	6,4	9	1,14	0,854
Образец 2	7,9	12	1,011	0,988
Образец 3	7,3	10	1,059	0,941
Образец 4	6,9	10	1,024	0,897
Образец 5	6,9	8	1,038	0,961

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

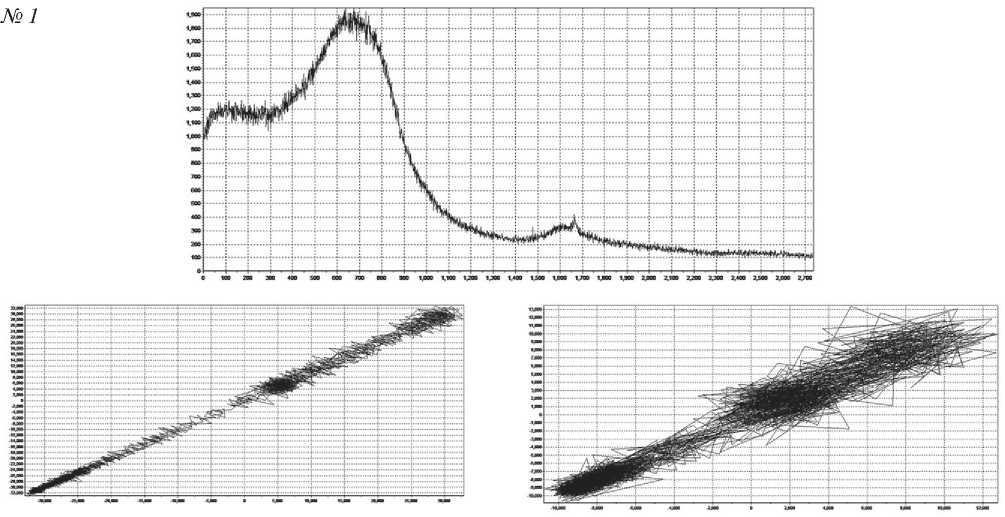
2D                                       3D

2D

3D

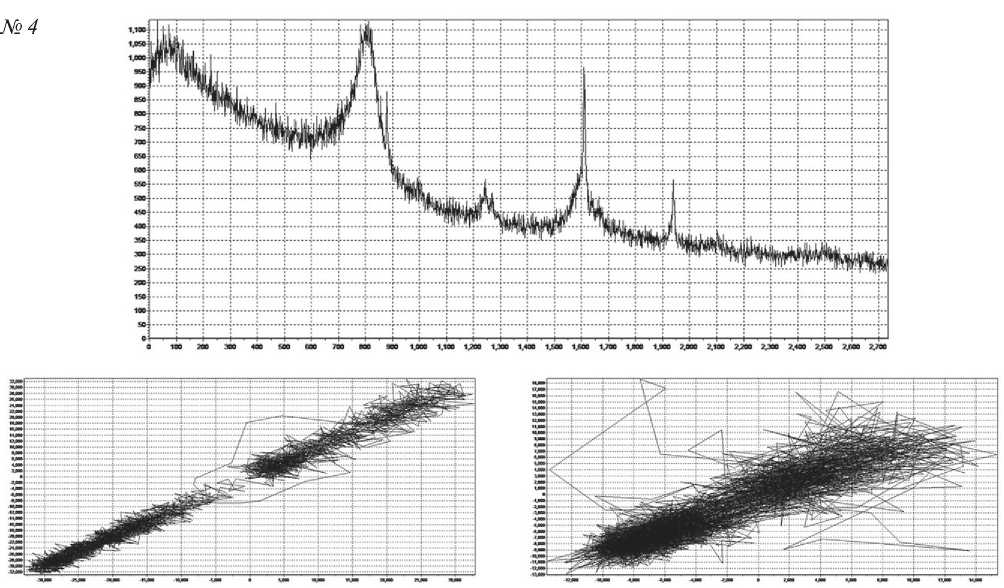
Рис. 6. Аттракторы образцов 1–5, построенные по результатам структурных измерений

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

2D

3D

Продолжение рис. 6. Аттракторы образцов 1–5, построенные по результатам структурных измерений

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

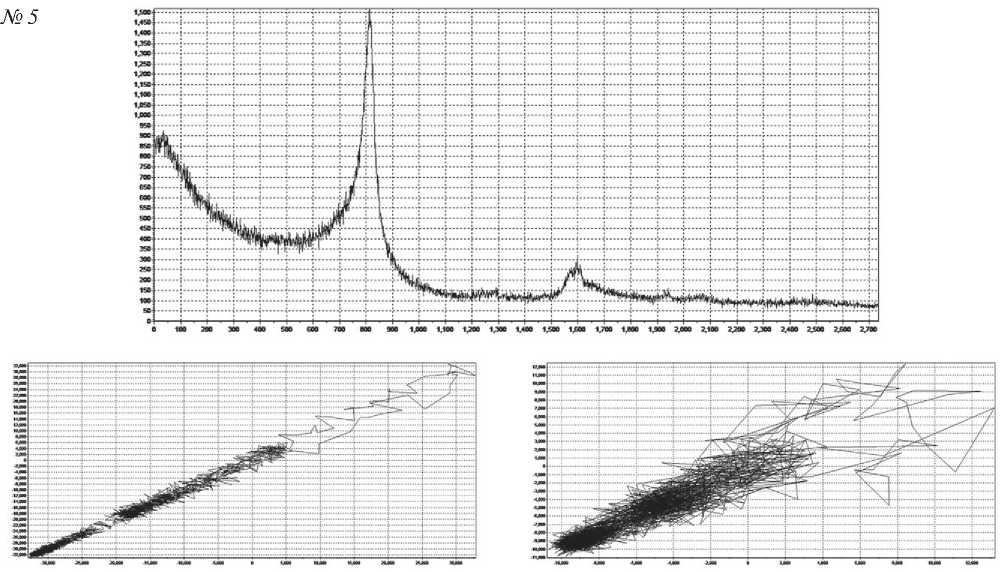
2D

3D

Окончание рис. 6. Аттракторы образцов 1–5, построенные по результатам структурных измерений

Образец 2

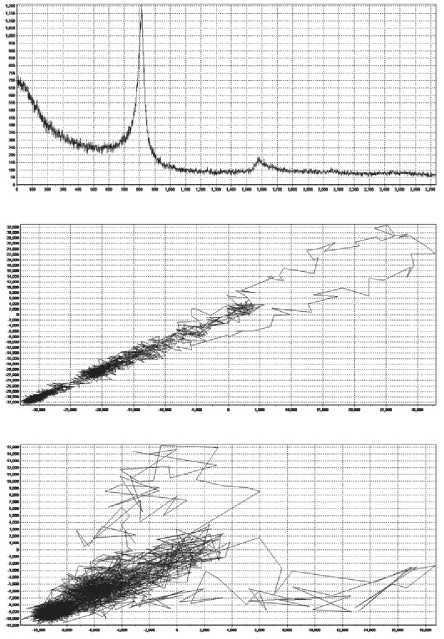
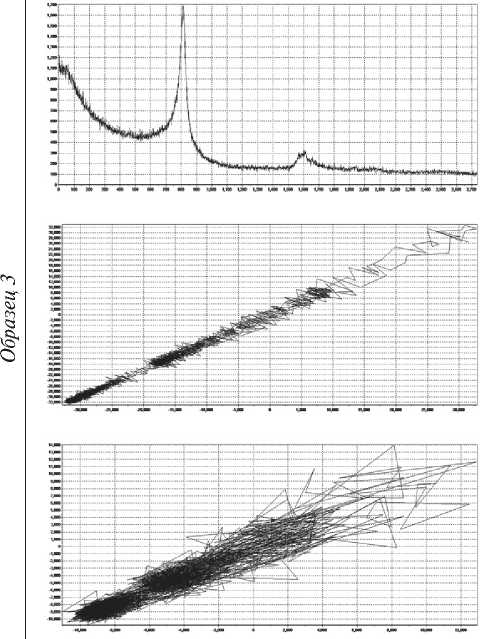
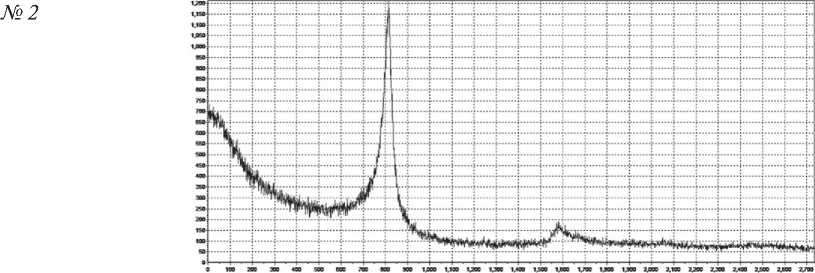
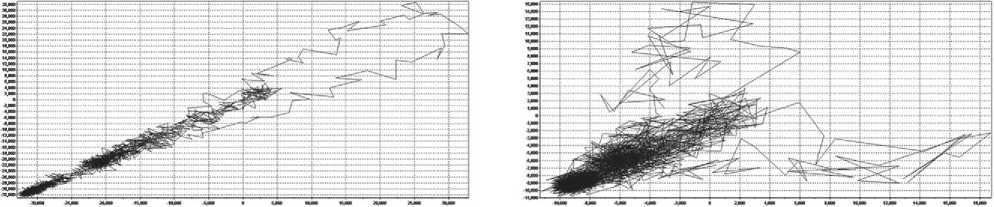
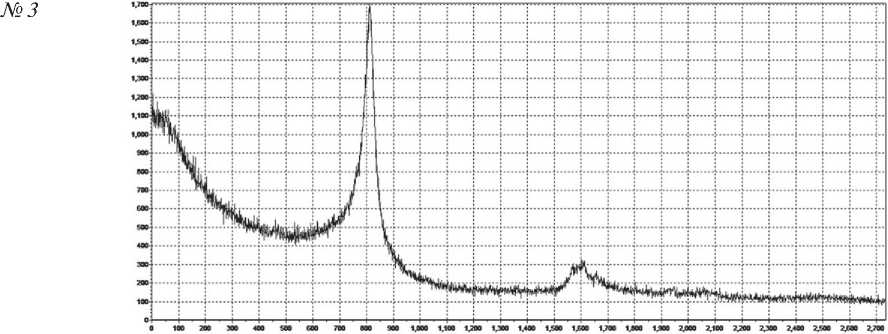
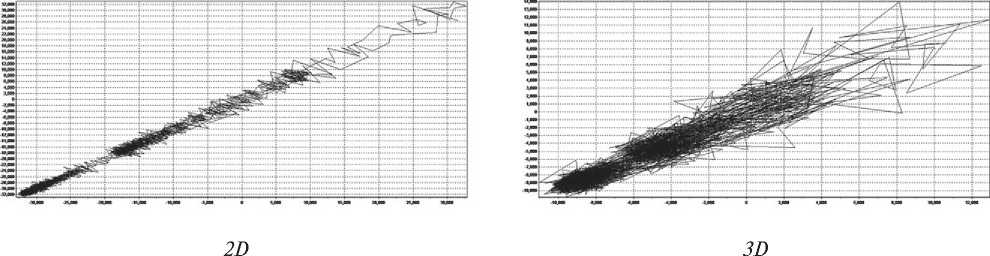
Рис. 7. Сравнение спектров и аттракторов образцов № 2 и 3. Структурные спектры

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ

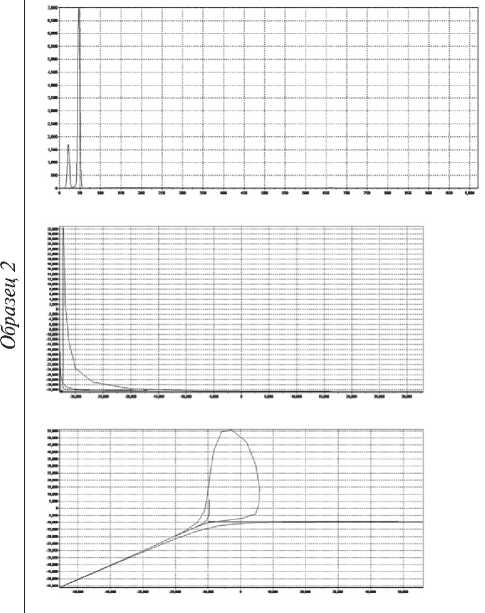
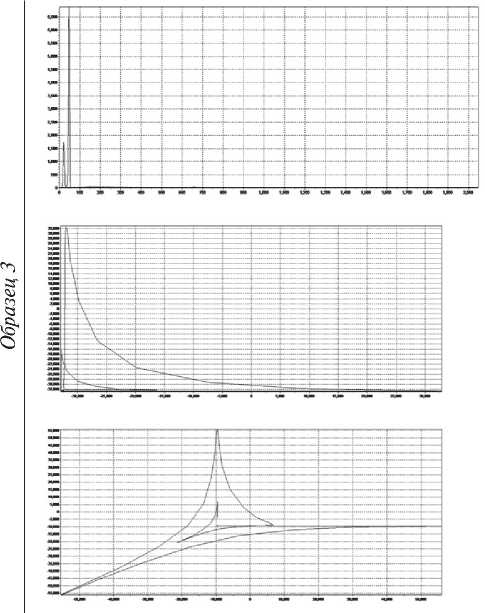
Окончание рис. 7. Сравнение спектров и аттракторов образцов № 2 и 3. Рентгенофлуоресцентные спектры

ВЫВОДЫ

При исследовании динамики химических реакций, протекающих в смесях с перемешиванием, активно применяется система дифференциальных уравнений Ресслера, соответствующих линейному осциллятору с отрицательным коэффициентом затухания и обратной связью: ( dy ² / d ² x )– a ( dy / dx )+ y = – z . Дифференциальная модель Ресслера служит примером многомерных систем, динамика которых допускает аппроксимацию одномерным отображением. Решением модели Ресслера при определенных параметрах является аттрактор Ресслера – притягивающее множество траекторий на фазовом пространстве, которое по своему виду идентично изучаемому процессу [14, 16].

Аттрактор Ресслера сгенерирован стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника, в случае синтеза – добавление необходимых компонентов и продуктов, получаемых в результате реакций. Физический смысл модели Ресслера описывает переход ламинарного движения жидкости к движению турбулентному.

Система дифференциальных уравнений, решение которой приводит к аттрактору Ресслера, имеет вид:

x · = – y – z , y · = x + ay , z · = b + z ( x +µ).

Модельный аттрактор Ресслера имеет вид, приведенный на рис. 8. 3D сечения аттракторов, полученные на основе рентгенофлуоресцентных спектров, близки к виду фазовой траектории Ресслера. Соответственно, можно оценить, опираясь на аттракторы, характерные для каждого образца (материала синтеза), на какой стадии находится процесс синтеза, и построить дифференциальную модель, осуществляя управление повышения качества продуктов выхода.

Несколько другой смысл имеют аттракторы, построенные на основе структурных измерений. При

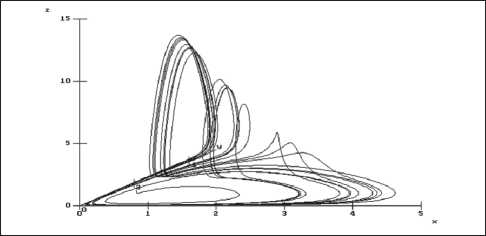
Рис. 8. Модельный аттрактор Ресслера

ПРИМЕНЕНИЕ НАНОМАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ В СТРОИТЕЛЬСТВЕ сравнении образцов № 2 и 3 видно, что процесс образования кристаллических структур находится в стадии развития при явном изменении аморфной фазы.

Таким образом, применение методов описания нелинейных динамических систем при интерпретации данных рентгеноспектрального и рентгенофазового анализа позволяет количественно оценивать степень упорядоченности углеродных наночастиц, определяющую их эффективность в качестве модификаторов строительных материалов.