Рентгеновская дифракция пространственно ограниченных пучков в латеральных периодических структурах

Латеральные периодические структуры (ЛПС), включая многослойные и кристаллические дифракционные решетки, структуры, модулированные внешним воздействием (например, ультразвуковой волной), находят широкое применение в нано- и оптоэлектронике, а также в рентгеновской оптике. Традиционно для описания рассеяния рентгеновских лучей на ЛПС используется модель падающей плоской волны, которая не ограниченна в латеральном направлении. Однако в процедуре сравнения измеренных и расчетных данных такая модель не совсем корректна, поскольку в эксперименте все рентгеновские пучки пространственно ограничены. Кроме того, в рамках модели плоских волн невозможно выполнить численный расчет распределения интенсивности рассеяния вблизи узла обратной решетки, так как угловые размеры дифракционных порядков описываются дельта функцией Дирака. Поэтому в данной работе теория рентгеновской дифракции обобщена на случай пространственно ограниченных рентгеновских пучков.

Теория

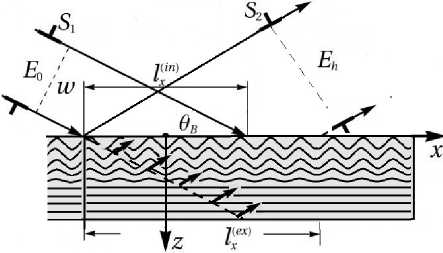
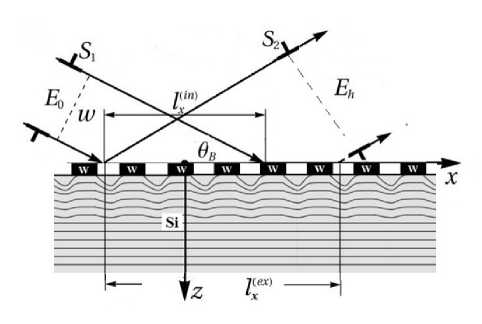
Рассмотрим дифракцию ограниченных рентгеновских пучков в кристалле, приповерхностная область которого состоит из периодически расположенных в латеральном направлении деформированных участков. Такое распределение упругих деформаций кристаллической решетки может быть создано в результате воздействия поверхностной акустической волны (рис. 1a), либо создания на поверхности кристалла периодической решетки из другого материала (рис. 1b). Для простоты рассмотрим симметричную дифракцию в геометрии Брэгга. Ширина за- светки поверхности кристалла падающим пучком зависит от размера щели S1 и равна lXin). Поперечный размер выходящего пучка формируется щелью S2, латеральная ширина которого на поверхности кристалла равна lXex) (рис. 1b). Дифракцией рентгеновских лучей на краях щелей падающего S 1 и отраженного S2 пучков пренебрегаем. Амплитудный коэффициент отражения (АКО) пространственно ограниченного пучка от ЛПС имеет вид

R ( q x ,q z ) =

a h

2 nl Xin )

+го l dkR^(K,qx,qz)

-∞

/X               /X

Y1(к)Y2(к - qx),    (1)

где R^(K,qx,qz) — АКО неограниченной плоской волны [1], функции sin (к lXin) /2)

K/ 2

/X

Y 1 ^{( к} )

Y 2 ( к - q _x )

sin ((к - qx) lXin) /2^) ( к — qx) / 2

определены в работе [2].

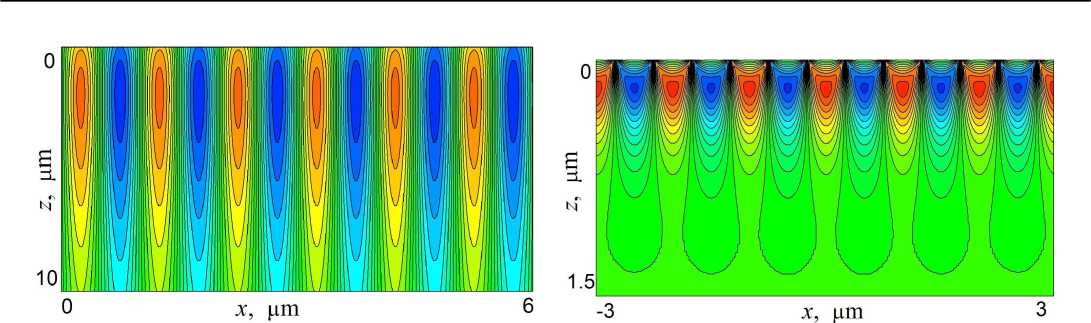
В рамках теории упругости выполнен численный расчет полей решеточных смещений в кристаллах ниобатлития ( LiNbO 3 ) и кремния. В первом случае периодические упругие деформации вызваны действием поверхностной акустической волны с периодом модуляции 4 цт (рис. 2a). Во втором случае деформации возникают из-за молекулярного взаимодействия атомов разных по химическому составу сред — полосы вольфрама шириной 0 . 5 цт периодически расположены на поверхности кремния, период металлической решетки равен 1 цт (рис. 2b).

(a)

(b)

Рис. 1. Схема дифракции ограниченных рентгеновских пучков на кристалле, промодулированном поверхностной акустической волной (а), и кристалле с поверхностной решеткой (b).

Fig. 1. Geometry of diffraction for spatially bounded X-ray beams on a crystal modulated by a surface acoustic wave (a) and a crystal with a surface grating (b).

(a)                                                                 (b)

Рис. 2. Поля упругих деформаций в кристаллах ниобата лития (а) и кремния (b).

Fig. 2. An elastic deformation field in lithium niobate (a) and silicon (b) crystals.

(a)

(b)

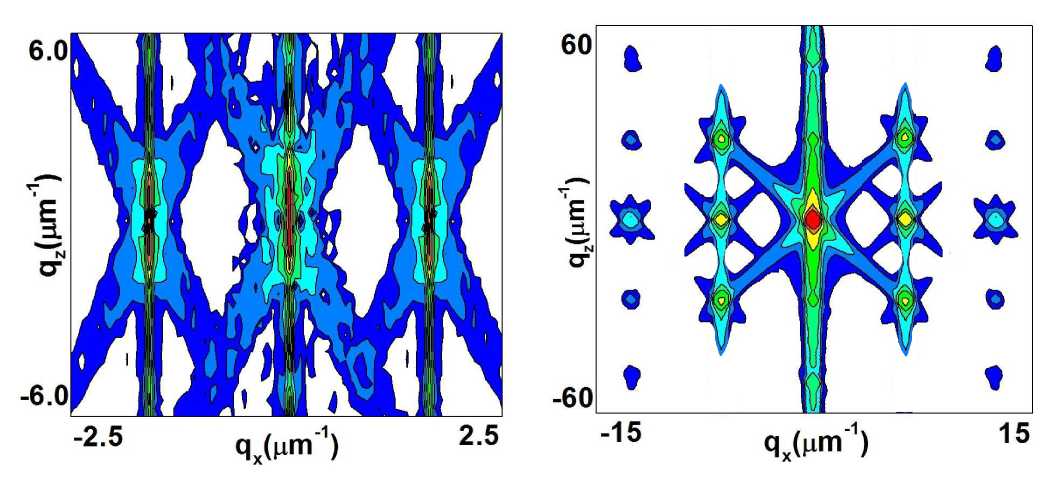
Рис. 3. Карты углового распределения интенсивности рассеяния вблизи узла обратной решетки от кристалла ниобата лития (a) и кремния (b).

Fig. 3. Reciprocal space maps of lithium niobate (a) and silicone (b) crystals.

На основе решения (1) выполнено численное моделирование углового распределения интенсивности рассеяния вблизи узла обратной решетки для кристаллов с разными периодическими деформациями. Для кристалла, промодулированного ПАВ, дифракционные порядки состоят из вертикальной полосы основного отражения и наклонных полос, вызванных ограниченностью рентгеновских пучков (рис. 3a). В случае дифракции на кристалле с поверхностной решеткой дополнительно наблюдаются сателлиты вдоль наклонных полос из-за модуляции падающего излучения (рис. 3b).

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН (проект 18-10-2-23) и РФФИ

(проект №17-02-00090).