Реологические модели растворов полимеров

Survey on the structural-phenomenological models of the solutions of polymers is represented. The construction of models is achieved into three stages: first, on the basis of the type of macromolecule, the geometric form of macromolecule is postulated, is examined the motion of the noninteracting macromolecule in the uniform hydrodynamic field on the microlevel, then, using Fokker-Planck equation it is produced passage to the macrolevel. Thus, are obtained evolutionary equation for the tensor parameter of order and equation for the macroscopic stress tensor as the functions of the achieved degree of the ordering of macromolecules. The type of objective derivative in the evolutionary equation automatically escapes from the geometric form of macromolecule.

Большинство волокнообразующих материалов – расплавы и растворы полимеров – это высокомолекулярные соединения со сложной молекулярной структурой, и их реологические свойства весьма сложны и разнообразны. Важнейшими характеристиками полимерной системы являются вязкость и упругость, значения которых определяются как условиями процесса – температурой, давлением, скоростью деформирования и т.п., так и молекулярной структурой полимерной системы.

Одним из наиболее важных этапов развития динамики макромолекул явилась концепция рептилии, введенная Де Женном [1-4] и обобщенная в дальнейшем Дои и Эдвардсом [5,6]. В модели Дои – Эдвардса каждая полимерная молекула рассматривалась как гибкая неудлиняющаяся цепь, движущаяся внутри трубки, образованной другими молекулами. Позже, благодаря исследованиям Волкова и Виноградова [7,8], Покровского [9–10], Марручи и Гриззути [11], модель Дои – Эдвардса была модифицирована для учета не только ориентации, но и удлинения каждого сегмента полимерной цепи. Результирующая модель (DEMG-модель) наиболее полно описывает динамику макромолекул, но очень сложна для численных расчетов реальных течений. В работах Рем-мелгаса, Харрисcона и Лила предложена относительно простая дифференциальная векторная модель [12–13] (RHL-модель), с высокой степенью точности аппроксимирующая предсказания более точной модели DEMG. В этой модели вся макромолекула описывается одним вектором, соединяющим начало и конец полимерной цепи. Этот вектор может удлиняться при удлинении макромолекулы и изменять ориентацию под действием внешнего потока и броуновского движения. Модель RHL сочетает простоту, физически точную основу, хорошее согласование с экспериментальными данными и широкие возможности для численных реализаций.

Изучение поведения растворов полимеров начинается с изучения движения отдельной макромолекулы в потоке растворителя. Рассмотрим движение не взаимодействующей макромолекулы в гидродинамическом однородном поле растворителя с градиентом скорости L = VvT. Пусть макромолекула представляет собой жесткую недефор-мируемую палочку. Ее можно характеризовать вектором R = Ru , где RiR = 1 нормированная длина палочки и u единичный вектор (|u| = 1). Выберем систему координат, связанную с центром палочки. Тогда u играет роль радиус-вектора конца палочки. Скорость растворителя в точке пространства, определяемой радиус-вектором u , есть производная по времени от u и равна и0 = L«u . Поскольку палочка не деформируется, скорость конца палочки отличается от скорости растворителя и имеет вид и = L«u-(uu: L)u .

Угловая скорость палочки ю = u x u = u x L«u - u x u (uu : L).

Второй член в правой части этого выражения равен 0, поскольку векторное произведение вектора на тот же самый вектор тождественно равно нулю, u x u = 0 .

Если рассматривать макромолекулу в виде сфероида (эллипсоида вращения) с полуосями a и b , то раскладывая градиент скорости на симметричную и антисимметричную части, L = W + D , получим

Р2 -1

ю = u x W « u + — u x D « u ,                        (1)

p ² + 1

где p = a/b . Это уравнение впервые было исследовано Джеффри [1].

В сферической системе координат при условии, что |u| = 1, уравнение (1) имеет вид

А . Р2 - 1 . „      „ .     _ 0 = y —2— sin 0 cos 0 sin ф Cos ф, Р 1+1                                                     (2) ф = y —----(Р2 cos2 ф + sin2ф), Р2 +1 где у = —x— градиент скорости вдоль направления у . Проинтегрировав эти уравне-Sy

ния, получим

Cp tg 0= ,------------------, Р 2 cos2 ф + sin2 ф                            m (3) 2 п t tg ф= р tg ( т +% )•

Здесь C и X - константы интегрирования, T - период полного оборота сфероида вокруг оси z :

T = — (Р + -).                              (4)

Y Р

Согласно уравнениям Джеффри конец вектора u описывает замкнутую траекторию по поверхности единичной сферы так, что через промежуток времени, равный периоду, ориентационная конфигурация сфероида полностью повторится. Это означает, в частности, что макроскопический тензор напряжений будет осциллировать во времени с периодом T . Другой чертой уравнения Джеффри является кинематическая обратимость. Изменив направление деформации на противоположное, мы вернемся к начальной конфигурации сфероида. Уравнение Джеффри допускает единственное стационарное решение ф = п/2 только для предельно анизометричных макромолекул p = от .

В этом случае через промежуток времени t = у -1 с начала деформирования сфероид ориентирован в направлении течения.

При рассмотрении движения ансамбля макромолекул следует иметь в виду, что в изотропном состоянии их ориентация носит стохастический характер и каждая отдельно взятая макромолекула начинает свое движение со своим случайным начальным условием. Таким образом, макроскопические свойства раствора полимера являются статистическими. Для описания движения ансамбля макромолекул следует прибегать к методам статистической физики.

Рассмотрим для начала диффузию макромолекул с учетом броуновского движения, следуя Дои и Эдвардсу [2]. Пусть C ( x , t ) концентрация макромолекул. Процесс диффузии описывается законом Фика,

J ( x , t ) = - D V C ( x , t ),                                 (5)

где J ( x , t ) – поток макромолекул, D – коэффициент диффузии. В дальнейшем, где не возникает недоразумений, явное указание на зависимость переменных от координат и времени будем опускать.

Уравнение (5) вместе с уравнением баланса dC d t

-V- J

дает известное уравнение диффузии ac

= D V- ( V C) = D ^ C. d t

Если существует внешний потенциал U ( x ), закон Фика должен быть модифицирован. Потенциал порождает силу, действующую на макромолекулу,

F = -V U ,                               (8)

и в результате получаем среднюю скорость, линейную по F ,

V = - Zv U .                               (9)

Константа Z называется коэффициентом трения, а обратная величина 1/ Z -подвижностью.

Из гидродинамических вычислений для сферы радиусом a и вязкости растворителя n s коэффициент трения

^Z = ^{6 П}П s a .

Средняя скорость макромолекулы дает дополнительный поток C v так, что общий поток

С

J = - D V C --V U.

Z

В состоянии равновесия концентрация C _eq ( x ) дается больцмановским распределением

C eq ( x ) « exp -I

U ( x )' ^k B ^T >

и поток должен исчезать,

- D V C_ea - ¹ C _e V U = 0. eq         eq

Из (12) и (13) следует соотношение Эйнштейна d=k T z

.

При подстановке (14) в (11) получаем

J = - !( kBT V C + C V U),

и уравнение диффузии принимает вид д C

ac r                   i

— = V- -kBTVC + CVU .

B

д t

По существу, это известное уравнение Фоккера–Планка, но поскольку оригинальное уравнение Фоккера–Планка записано в пространстве скоростей, то его часто предпочитают называть более общим уравнением Смолуховского.

Перепишем уравнение (16) в виде

J = -—V ( k B T In C + U ) ,

где k B T ln C + U - химический потенциал невзаимодействующих макромолекул концентрации C .

Если определить флуктуационную скорость потока как vf = J/ C , то из (17) получим vf =—1 V(kBT InC + U).

Тогда уравнение Фоккера–Планка (Смолуховского) можно записать в другой более простой форме,

— = -V-( C vj. д t ^v f’

Уравнение Фоккера–Планка для функции распределения плотности вероятности нахождения макромолекулы в данное время в данном месте T ( x , t ) имеет тот же вид, что и (19), так как между C и T отличие состоит только в том, что T нормирована (0 1), а C - нет.

Таким образом, можно записать

-— = -V-[TV(kBT lnT + U)]

или с учетом TV In T = VT переписать в эквивалентном виде:

1-— = ^V-( kBTVT + TV U).

Флуктуационную скорость макромолекулы можно разложить на трансляционную скорость центра масс и вращение макромолекулы относительно этого центра. Флуктуационная поступательная скорость центра масс макромолекулы не оказывает заметного влияния на макроскопические свойства суспензии, поэтому сосредоточим внимание на вращательном движении недеформируемых палочкообразных макромолекул с соотношением полуосей a / b ^ да . Угловая скорость в этом случае

ю = u х u = u х L - u.

Если на макромолекулу действует внешнее поле с потенциалом U , то макромолекула получает дополнительную угловую скорость ю = - ± ^(U ), Z r

где Ж u х ^() - векторный оператор бесконечно малого поворота, обладающий свой-du ством эрмитовости,

J A ( u ) Ж [ B ( u )] d u = - J Ж [ A ( u )] B ( u ) d u .

Дифференциальный оператор второго порядка Ж-Ж [ Т ] в сферической системе координат при |u| = 1

V2Tp . =Ж-ЖТ =---- (u=1)             sin3 53

f5T

sin 3 ---

1 52 T

+ —-2

sin 3 5ф

Итак, суммарная угловая скорость палочкообразной макромолекулы

ю =—— Ж U + u х L • u

Z r

или с добавлением броуновского потенциала k_BT ln T имеем угловую скорость

ю = —— Ж( kBT ln T + U) + u х L • u

Z r    ^X

и соответствующую флуктуационную скорость

v f = to х u .

Тогда уравнение Фоккера–Планка с учетом соотношения Эйнштейна для вращательной диффузии D r = k_BT Z r _r примет вид

^^ = -V- (v z^) = ——-(юх u^) = -fi 51 v f ’     5u v 7     (

= Dr ^-(^T + W U )-«-( u х L - uT).

.юТ = -Ж-(юТ) =

Эволюционное уравнение для среднестатистического тензорного параметра порядка (uu^ = J uu T d u можно получить, умножая (27) на uu и интегрируя по пространству всех направлений u . Используя свойство эрмитовости оператора Ж , в случае отсутствия внешнего поля U = 0 , уравнение (27) можно переписать:

5T

J ( u _a u p ) 5— d u = D r J Т [ Ж ² (u _a u p ) + ^ ( u _a u p ) - ( u х L • u ) ] d u .

Для дальнейшего преобразования (28) воспользуемся представлением векторного произведения через символы Леви-Чивита и правилами их перемножения, a Х b =Эrst asbt , u Х L • u =3rst usLtqUq ,

³ apy   PY«   yap       pay      ³ ypa      ³ ayp ’

• ³ krq ³ stq   ⁵ ks ⁵ rt   ⁵ kt ⁵ rs ,

э„ 3f = 5,5 -5Л = 35, -5, =25, , ktq stq ks tt kt ts ks ks         ks ,

³ ktq ³ ktq = ^{2 5} kk = ⁶ .

Отсюда следуют правила для оператора бесконечно малого поворота:

5 и в

³ a k в ^U k     ³ ap k ^U k ,

^K a ^U в =³ a kp ^U k д и ^=3< kp ^U k ⁵ p p

К К u„ = — 3 „ К и =3 „ 3 и = — 2 u„ , a a p apy a y apy ayp ц         p ,

д ( и _a и p )

К k ^{( U} a ^U p ) =³ kst ^U s ~_u ---=³kst ^U s [ 5 a t ^U p +5 p t ^U a ^] = U | ) ‘s a ^U p + ³ ks p ^U a ],

К k [ К k ( U a U p )] =3 kpq

5 f

^Up . U  ^{{ U} -  ’ ‘s a

^U p + ³ ks p ^U a ^{] }}

• ³ kps ³ ks a ^U p ^U p + ³ kps ³ ks p ^U p ^U a + ³ kp p ³ ks a ^U p ^U s + ³ kp a ³ ks p ^U p ^U s

= - ^{2 U} a ^U p - ^{2 U} a ^U p ^{+ ( 5} ap ^U s ^U s ^{— U} a ^U p ) ^{+ ( 5} ap ^U s ^U s ^{— U} a ^U p ) = ^{— 6 U} a ^U p ^{+ 2 5}

Учитывая, что и _a и p - базис фазового пространства, не зависящий от времени, изменим порядок интегрирования и дифференцирования в первом члене уравнения (28) и, руководствуясь приведенными выше правилами, получим эволюционное уравнение для тензорного параметра порядка ^uu^ :

D uu

Dt

= L • ^uu) + (uu^ • L T

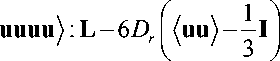
Аналогичным способом можно показать, что при рассмотрении сфероидальных макромолекул, вместо (29) будем иметь

D uu

Dt

— W • ^uu^ + (uu^ • W — G ( D • (uu^ + ^uu^ • D T )

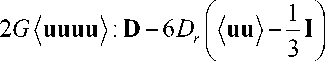
где G = ( p ² — 1)/( p ² + 1).

Следует подчеркнуть, что в предельных случаях для палочкообразных макромолекул (a » b, p ^ да и G ^ 1) в правой части уравнения (30) стоит верхняя конвективная производная по времени, для макромолекул в виде дисков ( a « b, p ^ 0 и G ^ — 1) -нижняя конвективная производная, а для сфер (a = b , p = 1 и G = 0) - яуманновская производная. Таким образом, тип объективной производной в эволюционных уравнениях для суспензий определяется геометрической формой макромолекул.

Полный тензор напряжения T можно представить как сумму изотропной составляющей - p I , тензора вязких напряжений т ( V ) и тензора упругих напряжений т ( E )

T = - p I + т( V) + т( E).(31)

Тензор упругих напряжений связан с изменением удельной свободной энергии A для виртуальных деформаций 5г

5 A = т(E) : 5.(32)

Свободная энергия определяется как

A = v j(kBTV ln TlTU) du ,(33)

где v число макромолекул в единице объема, а ее вариация

5 A = vj(kBT5V In T + kBT5V + 5VU) du .(34)

Вариация 5 ? вычисляется из уравнения Фоккера-Планка. Для малых деформаций £ градиент скорости L = 5е/ 5 1 доминирует над флуктуационным движением так, что

— = -^-(uXL• u?).(35)

Таким образом,

5T = -^(uxL • u?)51 = -^(ux5e• uT).(36)

Подставляя (36) в уравнение (34) и интегрируя по частям, получаем

5 Л = v j ( k_BT ( u x5 e • u )^T + ( u x5 e • u T)^ U ) d u =

= vj?(-kBT ^-( u x5e • u ) + (u x5e • u )-K U) du.(37)

Прямые вычисления с помощью приведенных выше правил для оператора бесконечно малых поворотов ^ приводят к следующему выражению для вариации свободной энергии:

5A V5, J?' 3^bTL.u,

^- 3 ⁵ «p

I a u p du =

= ^V& a _P

^{3 k} B ^TU a ^u p ^- 3 ⁵ «P

Отсюда тензор упругих напряжений имеет вид t^E) = 3vkBTi.u u --5aB ар         в \ a p 3 up

В отсутствии внешнего поля U = 0 , имеем

т ⁽ E ) = 3 v k_RT /uu - -1).

B ₃

Тензор вязких напряжений в общем случае пропорционален градиенту скорости и может быть записан в виде

( V )          ( V )

^L «p M «P^V L ^V ,                                          ⁽⁴¹⁾

где M ^ ^Vp_vv - тензор четвертого порядка, определяющий вязкие свойства трансверсально изотропной жидкости,

M kim = М о ⁵ И ⁵ km + M 1 ( ( ^U i ^U l ) 5 km + ⁵ im ^1 )) + M 2 ^Wm™ ) •

В случае палочкообразных макромолекул выражение для вязких напряжений можно конкретизировать:

С = П s ( L _а р + L p _a ) ^{+ vZ} st^U _а U р U ц U _v) L mv ,                      (42)

где n s - вязкость растворителя, Z _str — коэффициент трения.

Подставляя (40), (42) в (31), получаем выражение для полного тензора напряжений

T = ^- p I + 3 V ^k B T ^UU ^- 31^ + n s ( L _ap + L _pa ) + ^vZ str uu a ^u p ^u Ц ^u v ) L v .

Уравнения (43) и (30) не замкнуты, так как включают четвертый момент uuuu . Попытка построить уравнение для четвертого момента приводит к появлению бесконечной цепочки моментов более высокого порядка. Приемлемым приближением к точным уравнениям (30) и (43) является предложенное Дои и Эдвардсом замыкание через два момента второго порядка,

(uuuu) » (uu^uu^ .

Такая замена справедлива для состояний, близких к равновесному, и в пределе сильных течений. Для описания промежуточных интенсивностей течений Э. Хинч и Л. Лил [3] использовали другое разложение:

^uuuu: : L = (uuuu)

: D ® ¹

и получили систему реологических уравнений для сфероидальных макромолекул

D uu

Dt

= W • (uu^ + (uu) • W ^T + G [ D • (uu) + (uu) • D -

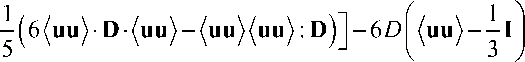
T = - p I + 2 ц ₀ D + 2 p ₁ ( (uu) • D + D • (uu) ) +

где D – коэффициент вращательной диффузии, G – параметр, зависящий от анизомет-ричности макромолекул, u – единичный вектор ориентации отдельной макромолекулы, ц0, ц1, ц2 - константы модели. Угловые скобки означают осреднение по всем направлениям. Единственным ограничением на величину uu является tr (uu) = 1.

Липскомб и Ден [4] проанализировали уравнение (46–47) с точки зрения зависимости коэффициентов вязкости р ₀, ц 1 , р ₂ от параметра G = ( p ² - 1 )Д p ² +1 ) , определяющего соотношение осей сфероида, и пришли к выводу, что при возрастании G от –1 до 0 ц ₀ уменьшается от +^ до конечного положительного значения, которое в дальнейшем при увеличении G от 0 до +1 не изменяется. Коэффициент ц 1 возрастает от -1 до 0 при –1 <  G < 0 и при положительных значениях G остается равным нулю. Коэффициент ц ₂ имеет абсолютный минимум при G =0 и резко возрастает как при отрицательных, так и при положительных значениях G .

Эта форма уравнений состояния достаточно полно описывает поведение растворов жесткоцепных полимеров и позволяет учесть эволюцию структурных изменений.

Растворы гибкоцепных полимеров представляют собой суспензию клубков переплетенных макромолекул, которые могут не только вращаться, но и вытягиваться под действием внешнего гидродинамического поля и броуновского движения. В работе [12] Реммелгас, Харисон и Лил предложили реологическую модель раствора гибкоцепных макромолекул полимера. Модель основана на следующих предположениях: надмолекулярная структура раствора полимера представима набором ориентированных деформирующихся клубков макромолекул; ориентационное распределение полностью описывается тензором ориентации второго ранга S , который представим как произведение скалярного параметра среднестатистического удлинения R ² и макроскопического тензора ориентации uu :

S = ^R Д (uu^,

где R = R u - вектор, соединяющий начало и конец полимерной цепи, причем в равновесном состоянии R = |R| = 1. Это ведет к появлению двух времен релаксации, связанных с релаксацией растяжения X _R и ориентационной релаксацией X d . В состоянии равновесия связь между временами релаксации дается соотношением X d = 3 N e X _R , где N e - характеризует число переплетений цепи. При сильной запутанности цепи N e >>  1 макромолекула возвращается в начальную конфигурацию много быстрее по длине, чем по направлению. Значительная часть полимерных макромолекул имеет большое, но конечное число переплетений, поэтому процессы переориентации и растяжения мы будем рассматривать отдельно, при этом предположим, что изменение ориентации R не будет существенно влиять на растяжение R .

Следуя стандартному подходу к рассмотрению движения макромолекул в потоке вязкой жидкости, состоящему в построении уравнения Фоккера–Планка для функции распределения плотности вероятности в пространстве всех конфигураций, рассмотрим деформирование клубка макромолекул под действием уравновешенной системы сил, которую можно определить как

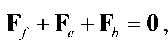
где F _f – силы гидродинамического трения, F _e – силы энтропийной упругости, F _b – броуновские силы.

Силы гидродинамического трения можно записать в форме

•

Ff =-Z(R) I R- L • R I, где Z(R) — коэффициент гидродинамического трения.

Энтропийная упругая сила не позволяет вытянуться макромолекуле на всю длину, что учитывается зависимостью упругих свойств от достигнутой степени вытяжки и записывается как

F =- к в Т f ( R ² ) R ,                            (52)

где f ( R ² ) – параметр энтропийной упругости, в общем случае возрастающая от единицы функция квадрата расстояния между концами цепи.

И, наконец, силы броуновского движения записываются в стандартной форме:

F =- к в Т V In V ,

где V - функция распределения плотности вероятности, нормированная условием j V dR = 1.

Флуктуационная скорость удлинения вектора R под действием этой системы сил определяется так: ⁱ

R = L • R - — f (R2) R - — V( In V),(54)

X R где XR = £/kBT - время релаксации удлинения.

Уравнение Фоккера–Планка с учетом введенной системы сил запишется как

• — = -v/ VR | = -V^(VL• R) + — V^Vf (R2)R] +—V-VV .(55)