Research design lining for utilities tunnel in the city based on state of "lining-massif soil"

• 1.    Introduction

• 2.    Basic theoretical principles

Microtunnelling is a special case of pipe jacking [5], where remote control of an automated microtunnel boring machine (MTBM) is employed. Excavated soil is removed from the face of the pipe jacking shield or MTBM and transferred to the surface for disposal while the shield or MTBM and the product pipes to be installed are driven through the ground using the force developed by a jacking frame installed in a fixed shaft.

For shallow burial jacked pipes, the jacking load will control the cross-sectional design of the pipe, and the soil pressure may be insignificant. However, for deep burial projects, high soil pressure may lead to the buckling of pipes [15], then the soil pressure becomes a crucial factor. Soil pressure on jacked pipes was also invoked to estimate the jacking force [11].

In current practices, the soil pressure on jacked pipes is estimated upon soil pressure models in Japan Microtunnelling Association (JMA), German standard ATV A 161 (ATV A 161), UK ‘Pipe Jacking Association’ (PJA), ASCE 27, and Chinese standard GB 50332 (GB 50332) [2, 6, 8, 12, 14].

These soil pressure models are modified from one of Terzaghi arching models (termed Arching model I) [13].

The design of technical tunnels shall be arranged in areas of weak sediment, weak soil characteristics, which exist in the initial stress domain, causing gravity, hydrostatic pressure, etc. The design of technical tunnels shall be arranged in areas of weak sediment, weak soil characteristics, which exist in the initial stress domain, causing gravity, hydrostatic pressure, etc.:

_σ ( _x 0)(0) _=σ ( _y 0)(0) _{=-γ H , σ} ( _x 0 _y )(0) _{= 0,    (1)}

where γ - the average volume weight of soil, H - depth of the development; " - " sign is adopted in accordance with the rule of elasticity theory, according to which the compressive stresses are considered negative.

Application of the principle of superposition can simulate a full voltage in an massif soil of soil in a neighborhood devel-

МИСиС

Национальный исследовательский технологический университет opment as the sum of the initial σ(0)(0) and additional σ(1)(0) (remove) the stresses caused by the formation of development. Thus, we can write:

σ(0)=σ(0)(0)+σ(1)(0),

where σ denotes all components of the stress tensor.

The concept of "removable stresses" was introduced by prof. I.V. Rodin [20] for simulating the formation of the production in a prestressed, massive massif of rocks. Using this concept, it is easy to imagine that in the formation of a development its contour must be freed from the total normal and tangential stresses. This can be achieved by superimposing stresses on the initial field around the generation of additional stresses of the same magnitude, but opposite in sign. Physically, this means that the initial stresses acting on the contour of the future development must be "lifted".

After installing the lining, which has a certain rigidity, depending on the thickness of the underground structure and the deformation properties of the material from which it is made, a redistribution of stresses occurs in the massif soil. In this case, in the case when the lining is installed directly into the face immediately after opening the section of the mine, the removed (additional) stresses acting on the side of the massif soil are completely transferred to it as a load (radial pressure). The lining is included in the joint work with the massif soil as an integral element of the unified deformable system "lining-massif soil". The calculation scheme for determining the permissible displacements of the massif soil and stresses in the support is shown in Fig. 1.

Having thus described the problem has an analytical solution presented, for example, in [16, 17]. Following the provisions set out in the above-mentioned works, altering the way to solve this problem. Assuming that development is not supported, then the contour L 0 massif soil (area S 0 ) boundary condition for the total stress in the polar coordinate system, taking into account the expressions (1), (2) can be written as:

a <⁰⁾ = _G (1)⁽⁰) + _G (⁰⁾⁽⁰) = _G (1)⁽⁰) -Y h = o. (3)

Here, the shear stresses are not considered due to the axial symmetry of the problem. Then, for the additional stress on contour unsupported produce the following relation:

^¹⁾⁽⁰⁾ = y H . (4)

Further, considering the case in which the development of the lining is installed, it should be noted that it prevents the free deformation contour L 0 development, creating resistance. For convenience, we consider the interaction of elements of a single system of "lining-massif soil", as shown in Fig. 2. Condition (4), taking into account the resistance lining takes the form:

a ( W) =y H - q о =- ( q 0 —Y H ), (5) where q ₀ - resistance lining.

A X

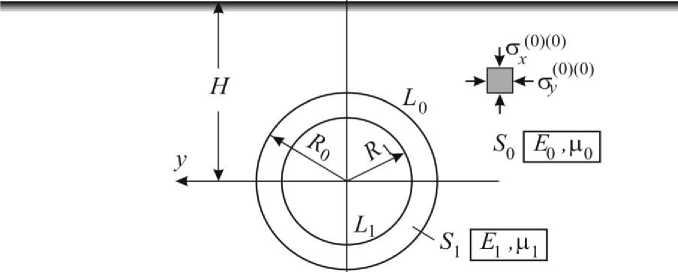
Fig. 1. Calculated scheme lining

МИСиС

Национальный исследовательский технологический университет

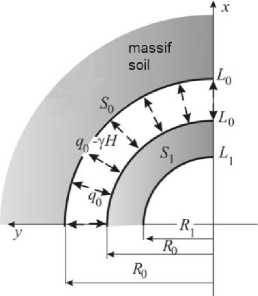
Fig. 2. The scheme of loading a single deformable system "lining-massif soil"

In (5) accepted that the normal stresses acting in the direction to the contour L 0 region S 0 , are compressed, ie negative. The outer loop support (ring S 1 ) having radial compressive stress q 0 , simulating mountain pressure on underground construction from the rock mass (the area S 0 ). Neglecting the initial stresses in the lining, we write the expression for the additional radial stresses in the ring S 1 in the contact line L 0 with an massif soil:

(1)(1)

СТ r ^-- q 0 . (6)

In the case where the lining is mounted directly to the face output, the solution of the problem can be obtained using a known solution of the problem of Lame [21]: the plane strain thick-walled pipe, simulating lining, the condition that the radial displacement at the line of contact between the lining and the massif soil due to the action of additional stresses (5), (6), we obtain the equation with respect to the value of resistance to q 0 . Taking into account the direction of stresses, and by putting in the formula Lame outer tube radius r 0 = ∞, the external pressure p 0 = 0, we write the expression for the movement of an infinite medium (massif soil) on the contour L 0 :

u 0 -- ., ( q . -Y H )• (7) 2 G ₀

where the notation: "-" sign in the expression (7) indicates that if the condition q 0 ≤ γ H point massif soil, located on the contour L 0 , shift into development.

E 0

G 0    2(1 + M о )

—

mechanical characte-

rization of soil, called the shear modulus.(8)

Equation (7) can be represented in the

form q 0 = f ( u 0 ), that is,

( q 0-yh 1 -

V

u o. ^{2 G} 0

, Y H J

^- Y H ^- u 0 tg P

2 G where tg p - —°- .

R 0

This relation (9) in the mechanics of underground structures is called the equation of equilibrium states of soil mass, since it implies that each value of resistance support (pressure on the lining) corresponds to a certain amount of movement of the circuit section of development. Further, the problem of putting in Lame outer tube radius r 0 = R 0 , the external pressure p 0 = q 0 , the inner radius r 1 = R 1 , and the internal pressure of p 1 = 0, we arrive to the second problem of plane deformation lining. We write the expression for the radial displacements of points of the outer contour of the lining: u 0 - Is, ^R^l [(1 - ^2ц1),02 + ,12!• (10)

The sign in the expression (10) is selected for the same reasons as in the formula (7), i.e. if q 0 > 0 point of the contour L 0 moved inside the ring (lining).

Equation (10) may also be present in the form q 0 = f ( u 0 ), and is easy to see, this relationship is linear. We represent it in the form of:

МИСиС

Национальный исследовательский технологический университет

q о = u o tg ^a ,            (и)

where the notation:

2 G    R 0 — R .²

^{tg a} = R — 2u 1/? 2 + R² . ⁽¹²⁾

^R 0 Lx ^{1 2} ^ 1 ) ^R 0 ^{+ R} 1 J

Equations (9) and (11) connect the same parameters q 0 and u 0 . We construct the corresponding graphic dependences together in one drawing, as shown in Fig. 3 [1, 10].

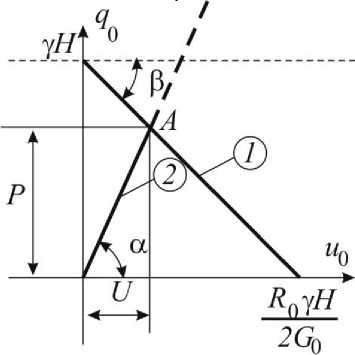
Fig. 3. Determination of the equilibrium state of a single deformable system "lining-massif soil"

Fig. 3 line 1 is a diagram of equilibrium states backed by generation, line 2 diagram of equilibrium states lining. Obviously, the point A of intersection of two charting will correspond to the equilibrium state of a single deformable "lining-massif soil". The value of q0 = P corresponds to the pressure on the lining (lining resist) with given geometrical and mechanical parameters set directly in the face, and the value of u0 = U — displacement massif soil in these geological conditions. The position of point A is determined by the combined solutions of equations (9) and (11): q о=YH ;4gp = tg a

1 + R ²

—

R

о

. (1) =

r

^— q 0 ; °,

.⁽ ex ) =

—

—

R

R

= YH

R

-

R

V

R

- 0 2

q 0 ;  (14)

- Lining on the inner loop L 1 :

°,

. ( in ) =

—

^-

R

₂ q ₀ . .

R

The internal forces and bending mo-

ments in the lining of the radial sections are

calculated from structural mechanics [18]:

N =

CT,

( in )

^“

+ O

( ex )

b A ;

M =

CT,

( in )

^-

^~

CT,

( ex )

b A ² ,

where A = R 0 — R = R₀ 1

—

R 1

\

^“

the thick-

V

+ G

G 1

( . — 2 M ) + 4

R ₀

.  (13)

ness of the lining, b = 1 m.

Considering expressions (14) — (15) of

the formula (16) take the form:

Additional stress in the lining (which are at the same time complete, because no initial stresses) are determined by the formulas:

- On the outer contour of the lining L 0 :

N =

—

q 0 R 0

b

³ + ib' ^R 0

1 + R ¹

;

V

M =

—

b 1

—

R 1

.

V

МИСиС

Национальный исследовательский технологический университет

The expression (17) allows you to test the strength of the lining.

Suppose, for example, the lining is made of concrete, which compressive strength is characterized by calculated resistance R b . Conditions strength bolting written in the form [18]:

| N | <  NS ,               (18)

where N - the calculated normal force, which is determined from the first equation (17), NS - limit bearing capacity of the radial section of the lining, which is determined

by the relation

NS = kR A b | 1-- ⁰ I , in

b I A J

which k = 1 , e ₀ =

M

N

- the eccentricity of

the application of the longitudinal force.

Using expressions (17), we write

NS = kR A b 1 -

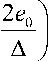
= kRR о f 1 -k

R ]

0 J

⁴²⁺ 512 k    R o J

33+к k R 0 J

Then the condition of the strength of the lining of sections (18) takes the form

Pu = q о <=

8 kR k

R 1²

^“ ---

^{2 +} R 2⁴

0 J

3 b

R ²

о J k    г>2 V

3 + R L

where: P u - limit pressure that can withstand considered bolting without loss of bearing capacity.

Thus, the line 2 in Fig. 3 characterizes the equilibrium state of the concrete lining, it should be limited to the point having ordinate q 0 = P u . This means that the strength of the lining will be provided if the condition:

P ≤ P u (21)

Significantly improve the static lining work is possible if it does not build directly at the bottom and install with some lag l 0 from the bottom. In this case, the diagram for the determination of the equilibrium state of the deformed system "lining-massif soil" is as shown in Fig. 4.

Here, as before, a straight 1 - equilibrium states supported by the diagram generation, 2 - line diagram of equilibrium states lining, erected at a distance l 0 from the bottom. A point of intersection of the graph corresponds to the equilibrium state of a single deformable system "lining-massif soil". For comparison, a straight 3 (dotted line) shows a diagram of equilibrium states lining being built directly at the bottom and a point B - appropriate occasion equilibrium. Offset massif soil u ( l 0 ), is implemented to the construction of the lining in the process of promoting the slaughter at a distance l 0 , characterized by the segment OO ^*.

k     ²¹0 J

q

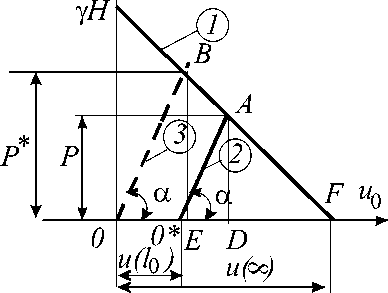
Fig. 4. Determination of the equilibrium state of geomechanical system "lining-massif soil" in the construction of the lining at a distance from the bottom l 0

МИСиС

Национальный исследовательский технологический университет

If development is unsupported for a long time (the lining is installed at a considerable distance from the bottom when l 0 →∞), all the possible displacement of the massif soil at this time and realized OF interval corresponds to a shift in the development of unsupported, that is, u (∞) = γ HR 0 /2 G 0 .

From Fig. 4 that the construction of the lining of the backlog of slaughter generation leads to a reduction of pressure on the lining, ie the condition P ≤ P ^*. The mechanics of underground structures [3] to account for this effect using the ratio:

P=P* α * or α *=P/P* .    (22)

Considering the similar triangles AEF and OBF, O ^* AD and OBE in Fig. 4, can be written:

* P AD O * A OF - OO *

а* =   ====

P * BE OB    OF

= "УУ = 1 - 4Ц = 1 - f (l0) (23) u (to )           u (to )

where f (k) = ^ = /'U, u(»)= RH -

' ^u (^to) f R^H V '   ² G o

TG

V  ^o 7

the bias circuit output, results from the decision of the respective plane problem for unsupported holes.

To determine the value of u ( l 0 ) should be considered three-dimensional picture surface deformations develop near the wellbore.

Research related to finding the displacement contour generation, depending on the distance to the bottom, in a large number of works, among which are the works of N.A. Davydov [19] and M. Baudendistel [4]. Deciding the proper task of the theory of elasticity in the volume setting using numerical methods such as finite element method, each of the authors offered their own formula for determining the value of f ( l 0 ).

Using a concrete representation for f ( l 0 ), being the substituted into the expres-

sion (23), arrive at the appropriate formulas for the calculation of the correction factor α^*. So, based on the results Baudendistela M., prof. N.S. Bulichev a result of the correlation analysis between the values of the ratio α ^* and the relative distance l 0 / R 0 to

slaughter generate suggested the use of the exponential dependence of [17]

f а * = 0,64 e

- 1,75 l У A .     /R o

.

V        7

Due to the linear nature of the problem, in geomechanics accepted accounting backlog of construction of the lining of the slaughter carried out by adjusting the initial stress field (1) intact massif soil. Then the corresponding components of the initial field multiplied by the value of α ^*, hence the initial stresses are determined by the formulas:

_а (0) ⁽ 0) = _а(0) ⁽ 0) = -^ н а * , т⁽ 0 ⁾⁽⁰⁾ = 0 . (25)

3. Conclusion

From the obtained ratio can be impor-

tant from a practical standpoint conclusions:

For example, from formula (16) that with

decreasing thickness of the lining

A = R o - R i = R o f l -V

R L R , 7

pressure on it is

reduced, and at R j ^ R the pressure is absent, that is, q 0 →0. In very soft ground, when the condition G 1 >> G _o ( G 1 - the shear modulus of the material lining) and can take G 0 / G 1 →0, the pressure q 0 in the lining tends to the value of the initial stress in the rock mass in its natural state, e.g. q 0 → γH .