Research of options of transition from unlimited to limited parallelism on the example of matrix multiplication
Автор: Romanova D. S.
Журнал: Siberian Aerospace Journal @vestnik-sibsau-en
Рубрика: Informatics, computer technology and management
Статья в выпуске: 1 vol.21, 2020 года.
Бесплатный доступ
Today, there are many approaches to developing parallel programs. It is considered that it is more efficient to write such programs for a particular computing system. The article proposes to ignore the features of a particular computing system and outline plans for the development of a certain automated system that allows trying to improve code efficiency by developing programs with unlimited parallelism, as well as explore the possibility of developing more efficient programs using the restrictions imposed on maximum parallelism. This approach was demonstrated on the example of the analysis of various matrix multiplication algorithms. As a mathematical apparatus, the study considered various approaches to the description of algorithms to increase their implementation, including an approach based on unlimited parallelism and, also, an approach based on various restrictions on parallelism is proposed. In the course of the work, sequential and parallel methods of matrix multiplication were studied in detail, including tape and block algorithms. As a result of the study, various matrix multiplication methods (sequential, with left and right recursion, parallel methods) were studied and more effective ones were found in terms of the resources used and the restrictions imposed on parallelism. A sequential method and a cascade summation scheme were analyzed and proposed as possible ways of convolving the results of solving the problem obtained after the decomposition stage. Also, a number of programs with different levels of parallelism were developed and implemented in the functional-stream parallel programming language. In the future, such transformations can be carried out formally, relying on a knowledge base and a language that allows equivalent transformations of the original program in accordance with the axioms and algebra of transformations laid down in it, as well as replacing functions that are equivalent in results and have different levels of parallelization. These studies can be used to increase the efficiency of developed programs in terms of resource use in many branches of science, including in the field of software development for the needs of astronomy and rocket science.
Unlimited parallelism, matrix multiplication, parallel programming.
Короткий адрес: https://sciup.org/148321716
IDR: 148321716 | УДК: 004.021 | DOI: 10.31772/2587-6066-2020-21-1-28-33
Текст научной статьи Research of options of transition from unlimited to limited parallelism on the example of matrix multiplication
Introduction. There are many different approaches for developing parallel programs. In parallel programming, special programming techniques are often used. And in most cases it is considered more efficient to write program code for a specific calculated system. Since the development of computer technology is proceeding at a rapid pace today, programmers have to rewrite code for a newly developed system. The main problem of the transition from traditional to parallel programming is that it is simply impossible to develop a universal executor with which it would be possible to achieve the same effective way of writing parallel programs [1–3]. In addition to the style of writing programs in a particular system, it is also necessary to take into account the amount of resources used and their computing power. Therefore, to implement effective parallel computing, you have to constantly rebuild the structure of the program.
The issue of creating tools to ensure portability of parallel programs has been studied for a long time. And all attempts to develop such systems were associated with writing programs for a generalized architecture [4].
It is proposed to focus not on the features of a particular computing system, but to use some kind of abstract system that allows trying to improve the efficiency of the code by developing programs with unlimited parallelism. Increasing the level of abstraction, it is possible to build various combinations, compressing parallelism, and therefore, the transition from unlimited parallelism to limited.
As a mathematical apparatus, the research considered various approaches to the description of algorithms to increase their implementation, including an approach based on unlimited parallelism. Also, the approach based on various restrictions on parallelism is proposed. In the course of the work, sequential and parallel methods of matrix multiplication were studied in detail, including band and block algorithms. After decomposition in the framework of solving the matrix multiplication problem, various options were proposed for the subsequent summation of the obtained results of solving subproblems in order to increase the efficiency of resource use in a consistent way and in a cascading manner.
These studies can be applied in various fields of science, including the development of software in rocket science, which will further improve the missile control system.
Main part. Algorithm for solving the problem. Statement of the problem. In fact, the statement of the problem is as follows. Two matrices are multiplied: A [M] [L] ∙ B [L] [N] => C [M] [N], where the number of row multiplications by columns is S = M ∙ N.
In each combination of row multiplication by column, L pairs of elements are involved.
Therefore, the total number of simultaneously possible multiplications P = M ∙ N ∙ L, that is, it is set by the corresponding parallelepiped [5; 6].
Next, the multiplied elements for each combination of rows and columns begin to add up. In this case, it is possible to use the usual sequential addition method or in a cascade scheme.
Matrix multiplication. Matrix operations are quite time-consuming to implement, so they represent a classic area of application for parallel computing.
Sequential Matrix Multiplication Algorithm
If there are two square matrices A and B, then C = A ∙ B is the result of their multiplication,
n
C ij = ^ = a ik ' b kj , (1)
k - 1
where i = 1, …, n , j = 1, …, m .
This algorithm for multiplying two matrices A and B is iterative and is oriented towards sequential calculation of rows of matrix C (fig. 1).
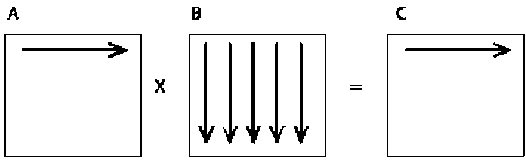
Fig. 1. First iteration of matrix multiplication in a sequential approach
Рис. 1. Первая итерация умножения матриц при последовательном подходе
When performing one iteration of the outer loop, one row of the resulting matrix is calculated [7].
In the sequential matrix multiplication algorithm, element-wise multiplication of all elements of the matrix occurs. The information graph in this case will be quite voluminous and therefore its analysis is difficult. In addition, this method of multiplication becomes ineffective if the size of the matrix exceeds the size of the processor cache. A search is needed for more efficient algorithms for solving this problem [8; 9].
From formula (1) it is clear that the calculation of each C ij is independent and simultaneously, and it can be performed in parallel. This algorithm is with mass parallelism, since it contains a huge number of operations that can be performed simultaneously and independently of each other [9].
The choice of matrix separation method leads to the determination of a specific parallel computing method; the existence of different data distribution schemes generates a number of parallel matrix computing algorithms.
If we ignore the use of specific resources to solve the problem, then we can achieve increased program efficiency, gradually compressing initially unlimited parallelism.
The process of multiplication in this case will begin with the decomposition of the task into subtasks. That is, to solve problem (1), we consider the main combinations of multipliable matrix elements in i , j , k .
Variants are possible when the resulting rows, columns or groups of matrix columns are computed in parallel. For example, if you execute the loop body in i for each counter value in parallel, then the rows of the matrix product will be counted in parallel. If we interchange the cycles in i and j (which is quite possible due to the independence of the operations of nested cycles in i and j ) and execute the body of the cycle in parallel for each counter value, we get a version of the program that contains columns in parallel. In addition, each element of the resulting matrix can also be counted in parallel [9].
Reduction steps when multiplying matrices and moving to parallel algorithms. As noted above, from the definition of the operation of multiplying the matrices A and B it follows that the elements of the resulting matrix C can be found independently of each other. The product of matrices can be considered as n2 independent scalar products, or as n independent products of a matrix by a vector. In both cases, different algorithms are used [10].
In the first approach, for organizing parallel computations, the main subtask uses the procedure of determining one element of the resulting matrix C, and for all necessary calculations, each task must contain at least one row of matrix A and a column of matrix B. The total number of subtasks here is n 2. In the second approach, to perform all the necessary calculations for the base subtask, one of the rows of matrix A and all columns of matrix B must be available. The number of subtasks is n [11].
To increase the efficiency of the matrix multiplication algorithm, it is logical to assume that if matrix multiplication is not performed element-wise, but line by line, this will make the algorithm more efficient in terms of parallelism. In this case, the general problem of matrix multi- plication will be reduced to dividing it into subtasks. Further, these subtasks will be combined to obtain a common necessary solution to the original problem.
Taking into account the foregoing, this algorithm can be considered as a process of solving independent subproblems of multiplying matrix A by columns of matrix B. At the same time, the information graph is simplified, in contrast to the case with a sequential multiplication algorithm. It all comes down to building a matrix multiplication graph. The introduction of macro operations is carried out in stages with a return level of detail of the operations or decomposition used [12].
Band algorithm. Consider band algorithms in which the matrices A and B are divided into continuous sequences of rows or columns (fig. 2). To carry out this procedure, each subtask contains row A of the matrix and access to columns B. One processor is allocated a number of rows and columns. A simple solution to this problem is to duplicate matrix B in all subtasks. Here the following way of organizing parallel computations for 3∙3 matrices is possible [13]:
Such fine-grained tasks can be enlarged if the matrix size is greater than the number of computing elements or processors. In this case, the original matrix A and the resulting matrix C are divided into horizontal stripes. In this case, the size of such bands should be chosen equal to k = n / p (if n is a multiple of p), which allows us to ensure distribution of the computational load across the computational elements uniformity [13].
The selected basic subtasks are characterized by an equal amount of transmitted data and the same computational complexity. In the case when the size of the matrices is greater than the number of computational elements (processors and/or cores) p, the basic subproblems can be enlarged by combining several adjacent rows of the matrix within one subproblem. In this case, the resulting matrix C and the original matrix A are divided into a series of horizontal stripes [13].
This band algorithm has good localization, and in addition, there is no interaction between data streams. But it should be noted that if we enlarge the subtasks, then we can move on to other matrix-multiplication algorithms that are more efficient in terms of parallelism – to block algorithms.
Transition to block algorithms. In such algorithms, the original matrices A, B and the resulting matrix C are represented as sets of blocks.
In this case, not only the resulting matrix, but also the matrix-arguments of matrix multiplication are divided between the threads of the parallel program into some rectangular blocks. This approach allows achieving good data localization and increased cache utilization.
Also there are well known parallel matrix multiplication algorithms based on block data division, oriented to multiprocessor computing systems with distributed memory. When developing algorithms focused on the use of parallel computing systems with distributed memory, it is necessary to take into account that placing all the required data in each subtask (in this case, placing the required sets of columns of matrix B and rows of matrix A in subtasks) will inevitably lead to duplication and significant growth of amount of memory used. As a result, some restrictions are imposed on the system, that is, the calculations must be organized in such a way that at each current point in time the subtasks contain only part of the data necessary for the calculations, and access to the rest of the data is ensured by sending messages. Algorithms that implement the described approach include the Fox algorithm and the Cannon algorithm [14] (fig. 3).
The difference between these algorithms is the sequence of transfer of matrix blocks between the processors of any computing system.
It should be noted that after the decomposition step with the allocation of subtasks and the search for an effective parallel algorithm, it is necessary to summarize the obtained solutions from the subtasks to get the general result of solving the matrix multiplication problem.
From the point of view of parallelism, one can apply in this case not only sequential summation, but also more efficient parallel methods, for example, addition according to a cascade scheme (fig. 4).
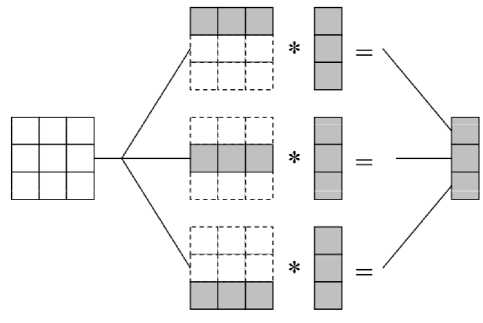
Fig. 2. The example of the organization of calculations in a matrix multiplication algorithm based on dividing matrices into rows
Рис. 2. Пример организации вычислений в алгоритме матричного умножения, основанного на разделении матриц на строки
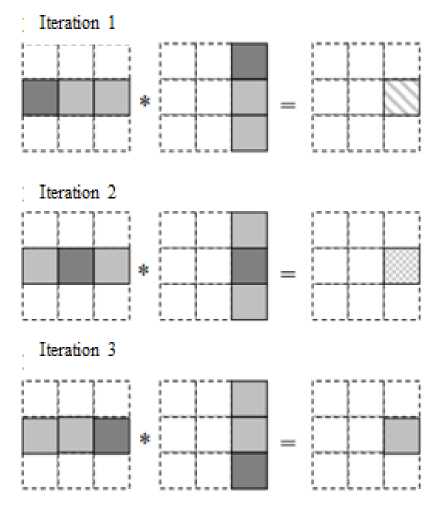
Fig. 3. Block matrix organization scheme
Рис. 3. Схема организации блочного умножения полос матрицы
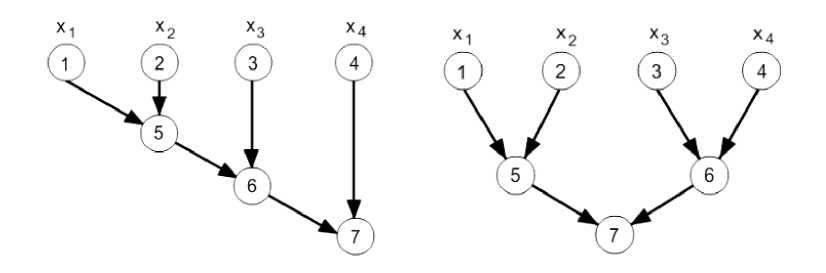
Fig. 4. Graphs of sequential (left) and cascade summation algorithms (right) [15]
Рис. 4. Графы алгоритмов последовательного (слева) и каскадного суммирования (справа) [15]
Conclusion. After the analysis of the above algorithms, it is planned to use the results to find the capabilities of equivalent transformations of various algorithms and to develop an automated system that allows its user to choose one or another algorithm to solve their problem in order to achieve the fastest and most effective solution with point of view of resources use.
Using algorithms that describe the maximum parallelism of the problem being solved, the developer offers additional methods for analyzing and deriving various algorithms with limited parallelism, which can be considered as use cases.
Consideration of all the algorithms studied in this paper, as well as their implementation in a functional dataflow parallel language that allows performing operations with maximum parallelism, opens up prospects for the further development and improvement of methods and approaches to enhance program efficiency.
Acknowledgments. This work was supported by the financial support of the Russian Fund of Federal Property in the framework of the scientific project No. 17-07-00288 A.
Список литературы Research of options of transition from unlimited to limited parallelism on the example of matrix multiplication
- Legalov A. I. Sovremennie problem informatiki i vichislitel’noi tehniki [Modern problems of computer science and computer technology: a training manual]. Tomsk, Publishing House SPB Graphics, 2012, 216 p. (In Russ.).
- Legalov A. I. [Sorting methods obtained from the analysis of the maximum parallel program. Distributed and cluster computing]. Izbrannie materiali 3 chkoli seminara. Institut comp’uternogo modelirovatiya SO RAN. Krasnoyarsk, 2004, P. 119–134.
- Legalov A. I. [On the management of computing in parallel systems and programming language]. Naychnii vestnik NSTU. 2004, No. 3 (18), P. 63–72 (In Russ.).
- Voevodin V. V., Voevodin Vl. V. Parallelnie vichisleniya [Parallel computing]. SPb., BHV Petersburg Publ., 2002, 608 p.
- Solomonik E., Demmel J . Communicationoptimal parallel 2.5D matrix multiplication and LU factorization algorithms. Department, University of California, Berkeley (February 2011), Available at: http: //www.eecs.berkeley. edu / Pubs / TechRpts / 2011 /EECS-2011-10.html (accessed 01.12.2019).
- Dongarra J. J., Duff L. S., Sorensen D. C., Vorst H. A. V. Numerical Linear Algebra for High Performance Computers (Software, Environments, Tools). Soc for Industrial & Applied Math.P, 1999, P. 120–128.
- Gergel V. P., Fursov V. A. Lektsii po parallel’nim ichisleniyam [Lectures on parallel computing: textbook]. Allowance. Samara, Samar. State Aerospace. University Publ., 2009, 164 p.
- Legalov A. I., Kazakov F. A., Kuzmin D. A., Privalikhin D. V. [The model of functional-stream parallel computing and the Pythagoras programming language. Distributed and cluster computing]. Izbrannie materiali vtoroi chkoli seminara. Instityt Komp’uternogo modelirovaniya SO RAN. Krasnoyarsk, 2002, P. 101–120 (In Russ.).
- Legalov A. I. [Sorting methods obtained from the analysis of the most parallel program. Distributed and cluster computing]. Izbrannie materiali tret’ei chkoli seminara. Instityt Komp’uternogo modelirovaniya SO RAN. Krasnoyarsk, 2004, P. 119–134 (In Russ.).
- Wirth N. Algoritmi i stryktyri dannih [Algorithms and data structures]. Moscow, Mir Publ., 1989, 360 p.
- Fedotov I. E. Modeli parallel’nogo programmirovaniya [Parallel Programming Models]. Moscow, SolonPress Publ., 2012, 384 p.
- Legalov A. I., Nepomnyaschy O. V., Matkovsky I. V., Kropacheva M. S. Tail Recursion Transformation in Functional Dataflow Parallel Programs. Automatic Control and Computer Sciences. 2013, Vol. 47, No. 7, P. 366–372.
- Miller R., Boxer L. Posledovatel’nie i parallel’nie algoritmi: obshii podhod [Serial and parallel algorithms: General approach]. Moscow, BINOM. Laboratory of Knowledge Publ., 2006, 406 p.
- Lupin S. A., Posypkin M. A. Tehnologii parallel’nogo programmirovaniya [Parallel Programming Technologies]. Moscow, Forum, Infra-M Publ., 2008, 208 p.
- Herlihy M. The Art of Multiprocessor Programming. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA. 2008, 508 p.


