Research on Fine-grained Job scheduling in Grid Computing

Published Online October 2009 in MECS

• I.    Introduction

  The growing popularity of the Internet/Web and the availability of powerful computers and high-speed networks at low-cost commodity components are changing the way we do computing and use computers. The interest in coupling geographically distributed resources is also growing for solving large-scale problems [18]. The word ‘grid’ was first coined in the mid-1990s to denote a proposed distributed computing infrastructure for advanced science and engineering projects [1]. The concept of a computational grid is intended to use high-performance network technology to connect hardware, software, instruments, databases, and people into a seamless web that supports a new generation of computationally rich problem-solving environments for scientists and engineers [2]. Resource sharing therefore is the essence of grid computing. And nowadays, around the issue of task scheduling in Grid computing, a lot of researches have been carried on.

There are a wide range of heterogeneous and geographically distributed resources in grid, such as computational resource, storage resource, equipment resource, and so forth. Grid resources are geographically distributed across multiple administrative domains and

Manuscript received January 11, 2009; revised June 22, 2009; accepted July 25, 2009.

owned by different organizations. Resource management and application scheduling are very complex due to the large-scale heterogeneity presented in resources, management policies, users, and applications requirements in these environments.

Consequently, many researches are motivated in different aspects of the job scheduling algorithm. One motivation of grid computing is to aggregate the power of widely distributed resources, and provide non-trivial services to users [14]. But, there exist several applications with a large number of lightweight jobs [3].

Sending some fine-grained jobs to a resource that can support high processing capability is not economical compared with sending a coarse-grained job. Unlike coarse-grained job, the lightweight job just has few lines of codes or very simple arithmetic expressions. Because the overall processing time for each job includes job scheduling time, job transmission time to a grid resource, job executing time, and transmission time of output, finegrained jobs spend too much time in scheduling and transmission. That means in the case of an application with a large number of jobs with small scale processing requirements, the total communication time between each job and the resource seems to be more than the total computation time of each job at the resource. Meanwhile, it is wasteful to process a lightweight job with a highly capable computer. The total overhead of fine-grained jobs scheduling can be reduced by grouping the lightweight jobs during the scheduling process for deployment over the grid resources. Then we can schedule the coarsegrained jobs which lightweight jobs grouped as in the grid environment. Because of reducing transmission time and increasing the cpu utilization, we can Significantly enhance the efficiency of system. This paper mainly focuses on fine-grained jobs scheduling in a grid, how they are grouped into coarse-grained jobs, and how they are allocated. An Adaptive Fine-grained Job Scheduling (AFJS) algorithm is proposed. Numerical experiments illustrate the efficiency of the proposed algorithm compared with the algorithm in [3]. And several important problems that brought by group algorithm in lightweight jobs scheduling are also illustrated in this paper.

The remainder of this paper is organized as follows. The current task scheduling algorithm is surveyed in section II. The AFJS algorithm is discussed in section III. With the help of GridSim toolkit [6, 12], the simulation of scheduling algorithm proposed in the paper is realized in section IV. In section V, two important problems— security and fault tolerant mechanism are illustrated. The final section concludes the paper with discussion and analysis of results.

• II.    Related Work

At present, there are some famous resource scheduling system and projects in the world, such as AppLeS, Globus, Condor, Legion, Nimrod-G, etc. And a great number of algorithms, approaches and tools have been developed to bring grid resource management and job scheduling issues to a more advanced level of efficiency and usability. Scheduling problem is a NP-Complete problem [10], which means that ordinary algorithms with non-optimization are impractical. Current job scheduling algorithms are mainly based on User-Directed Assignment (UDA), Minimum Completion Time (MCT), Minimum Execution Time (MET), Min-Min [7], MaxMin [13], genetic algorithm (GA) [15], ant algorithm (AA) [8], multi-Agent, computational economy model [4, 9,20], and so on. All of these algorithms are dedicated to improve the Qos of grid computing. One of the most important aspects of Qos is the jobs processing time. In fine-grained jobs environment, jobs processing time is also the first thing we should consider.

A scheduling optimization method should consider the following two aspects, one is the application characteristics, and the other is the resource characteristics [11]. Taking into account the characteristics of lightweight job, there are some researches on the fine-grained job scheduling problem. In [3], N. Muthuvelu, et al. presents a scheduling strategy that performs dynamic job grouping activity at runtime and gives out the detailed analysis by running simulations. However, there are some defects in the scheduling algorithm. First, the algorithm doesn’t take the dynamic resource characteristics into account. Second, the grouping strategy can’t utilize resource sufficiently, especially when the million instructions (MI) of jobs are quite different. And finally, it doesn’t pay attention to the network bandwidth and file size. To solve the problems mentioned above, an adaptive fine-grained jobs scheduling algorithm is presented in this paper. Numerical experiments illustrate the efficiency of the proposed algorithm.

And some other problems should be reminded in finegrained job scheduling environment. First, due to the characteristics of grouping algorithm, it is hard to prevent injection attacks. Some malicious customs can submit some fine-grained virus to damage the computing process of the coarse-grained job which contains the virus. Secondly, in commercial grid environment, resources are paid. Resources compute the grouped jobs instead of the original fine-grained jobs that customs upload. If we adopt the grouping algorithm, how to processing error is also an important issue in fine-grained job scheduling environment.

• III.    Fine-grained job scheduling mechanism

• A.    Definition of fine-grained job

In grid computing, we use MI as the unit of jobs. MI is million instructions or processing requirements of a user job. If the MI of a job is less than a fixed threshold M _max , we consider it as a fine-grained job. And it will be scheduled by fine-grained job scheduling algorithm. In Fig.1, this process has been depicted.

ordinary job

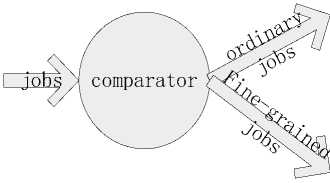
Figure 1. Job classification.

scheduling algorithm

Fine-grained job schduling algoritm

• B.    Resource monitoring

Due to nodes which are carrying resources joining and leaving the network at any time, the available resources change dynamically over time. The highly distributed and dynamic nature of grids makes the resource monitoring more challenging [19]. The grouping strategy should be based on the characteristics of resources. In grid computing, there are two approaches for obtaining dynamic resource characteristics for job execution. One is that a user directly searches the resources for job execution using an information service. The other is to use a resource manager. With a resource manager, users can obtain information about the grid through an interactive set of services, which consists of an information service that is responsible for providing information about the current availability and capability of resources. Obviously, the latter one is more convenient.

In order to obtain the latest details of grid, our resource monitoring mechanism is based on GRIM prototype and GRIR protocol [5]. As illustrated in Fig. 2, resource characteristics on which the grouping strategy is based are obtained from mediators. The updated status of resource information is actively transferred from resources to the mediator in the push-based model. To balance information fidelity in mediators and updating transmission cost between hosts and mediators, GRIR protocol is presented in [5]. Then we can schedule finegrained jobs based on the latest details of grid.

mediator

Figure 2. Mechanism for resource monitoring

• C.    Grouping constraint conditions

Based on the resources status, lightweight jobs can be grouped into coarse-grained jobs according to processing capabilities (in MIPS) and the bandwidth (in Mb/s) of the available resources. Here only the processing capacity and bandwidth are used to constrain the sizes of coarsegrained jobs, but we can easily join additional constraint conditions.

Then the fine-grained job can be grouped into several new jobs and these new jobs should satisfy the following formula:

gTOuPedjob _ MI i <  MIPS, * T_CO m _p _i , (1) groupedjob _ file _ size , = baud _ rate, * T_comm ,, (2)

T .1 T . = u. >  1. (3) comp _ i comm _ i i .

In constraint conditions, MIPS_i is the processing capacity of the resource i that the groupedjob_i will be allocated to, T_{comp _ i} is the expected job processing time, groupedjob _ file _ size_i is the file_size (in Mb) of the grouped job i , baud _ rate_i is the bandwidth of resource i , and T_{comm i} is the communication time. Formula (1) means that the processing time of the coarse-grained job shouldn’t exceed the expected time. For the parallel processing to make sense, that is to ensure that running a parallel program on several processors is faster than sequential execution, the calculation time should exceed communication time, and this is illustrated as (2)(3).

• D.    Grouping strategy

To maximize the MI of the grouped job we schedule, greedy selector and binary search are used. First the finegrained jobs should be sorted. The bucket sort is adopted to sort the fine-grained jobs. Bucket sort, or bin sort, is a sorting algorithm that works by partitioning an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a cousin of radix sort in the most to least significant digit flavour. Bucket sort is a generalization of pigeonhole sort. Bucket sort is a linear sort algorithm, the time complexity is O ( n ). The pseudocode of bucket sort is depicted in Fig. 3.

function bucket-sort(array, n) is buckets ← new array of n empty lists for i = 0 to (length(array)-1) do insert array[i] into buckets[msbits(array[i], k)]

for i = 0 to n - 1 do next-sort(buckets[i])

return the concatenation of buckets[0], ..., buckets[n-1]

• Figure 3.    Bucket sort

Then we group the fine-grained jobs by descending order. When the first fine-grained job that doesn’t satisfy restricted conditions appeared, binary search and backtracking is adopted to search the next fine-grained job that satisfies constraint conditions to join the coarsegrained job.

A binary search algorithm (or binary chop) is a technique for locating a particular value in a sorted list. The method makes progressively better guesses, and closes in on the location of the sought value by selecting the middle element in the span (which, because the list is in sorted order, is the median value), comparing its value to the target value, and determining if it is greater than, less than, or equal to the target value. The time complexity of binary search is O (log n ) . One of the pseudocodes of binary search is depicted in Fig.4.

int BinSearch(SeqList R ， KeyType K)

{ int low=1，high=n，mid； while(low<=high){ mid=(low+high)/2； if(R[mid].key==K) return mid； if(R[mid].key>K)

high=mid-1;

else low=mid+1；

} return 0；

} //BinSeareh

• Figure 4.    Binary search

Backtracking is a general algorithm for finding all (or some) solutions to some computational problem that incrementally builds candidates to the solutions, and abandons each partial candidate c ("backtracks") as soon as it determines that c cannot possibly be completed to a valid solution.

If job_n is the first fine-grained job that doesn’t satisfy the restricted conditions, we will use n and 1 as the two actual parameter of the binary search. In the next loop, the return value of the binary search will be the second actual parameter, and the low value that has computed the return value will be the first actual parameter of binary search.

For example, if job,n+1)/4 is the first job satisfying the conditions. n /2 and (n +1)/4 will be the new actual parameter of the binary search. If the return value of this loop is zero, job,n+1)/4 will be next fine-grained to join the coarse-grained job. We use stack structure to store the jobs satisfy the constraint conditions. And the top of the stack is the next fine-grained job to join the coarsegrained job. This algorithm is not an optimum one, but it can maximize the MI of the grouped job with a lower time complexity of the algorithm.

• E. fine-grained job scheduling algorithm

As is shown in Fig.5, AFJS algorithm is divided into three parts. The first phase is the initialization phase. In the first phase, the scheduler receives resources status using the mechanism demonstrated in the section B. Meanwhile, it sorts job list in descending order, and assigns a new ID for each job. And we define Con_{i , j} as the constraint conditions.

Algorithm:

Begin

Phase 1 : Initialization

• 1.    The scheduler receives jobs from users.

• 2.    The scheduler gets resources status from mediator.

• 3.    According to the MI of jobs, job_list is sorted in descending order using bucket sort algorithm. And each job is assigned a new ID.

• 4.    Define constraint conditions value Con_{i , j} is

( groupedjob _ MI j + job <  MIPS * ^T c _O m _p _j, and

( groupedjob _ file _ size j + job _ file _ size )

/baud rate, <      , )                  or j comp j

(groupedjob_MIj=0,                        and jobi/MIPSj>job_file_size/baud_ratej )

Phase 2 : Job Scheduling and Deployment

• 1.    for resource j in resource_list do

• 2.    {

• 3.      for i:=1 to joblist_size do

• 5.           if ( Con_{i , j} )

• 6.{

• 7.          add job i to job group j ;

• 8.         remove I from joblist;

• 9.i++;

• 10.}

• 11.    else

• 12.{

• 13.n=1;

• 14.        while (n)

• 15.{

• 16.        n=binarysearch(the low value of last

• 17.         if (n!=0) push_stack();

• 18.}

• 19.}

• 20.      if (!empty_stack())

• 21.{

• 22.      i=pop_stack();

• 23.      Clear_stack();

• 24.      add job i to job group j ;

• 25.      remove i from joblist;

• 26.      i++;

• 27.      }

• 28.    }

• 29.    j++;

• 30.    }

• 31.    for i:=1 to groupedjoblist_size

• 32.    {

• 33.    allocate groupedjob i to resource i ;

• 34.    }

loop, n);

Phase 3

• 1.    if joblist_size!=0

• 2.    {

• 3.       wait a minute;

• 4.       get resource status from mediator;

• 5.    receive computed grouped jobs from resources;

• 6.    repeat pahse2;

• 7.    }

• 8.    receive computed grouped jobs from resources

• 9.    split the output before presenting to the user End

• Figure 5. AFJS algorithm

Phase 2 is the process of job scheduling and deployment. In phase 2, given a list of resource, a match grouped job will send to the appropriate resource. First, we group the fine-grained jobs one by one until the first job that didn’t satisfy the conditions appear. Then we use binary search to find the next fine-grained job join the grouped job. The job we found is the job that satisfies constraint conditions with the maximal MI. This method could sufficiently utilize the capability of the resources since the grouped jobs match the MIPS of resource in a more proper way. To group a fine-grained job, the time complexity O ( T ) satisfies:

O ( n log n ) <  O (T ) <  O ( n 2 )               (4)

In the scheduling process, since the sort algorithm we adopt is a linear sort algorithm, the time complexity of our scheduling algorithm O ( H ) satisfies:

O ( m * n log n ) <  O ( H ) <  O ( m * n 2 )          (5)

In formula (4) (5), m is the number of resource, and n is the number of fine-grained jobs.

In the phase, when there is no more resource left, first come first served (FCFS) algorithm is used, once a resource node finishes its job, the mediator will get the status of the idle resource, and it will be assigned a new grouped job that grouped By AFJS. Compared with the round-robin algorithm used in [3], this algorithm reflects the dynamic grid environment more suitably especially when new resources are discovered constantly by resource manager. Then, the scheduler receives computed grouped jobs from resources and split the output before presenting to the user. And it will charge customs in economic grid environment.

• IV. Experiments

• A.    Experimental setup

  We simulated the proposed approach using GridSim toolkit and implemented the scheduling algorithm on a laptop with Core 2 T7250 processor and 1 G RAM. The

TABLE I.

A ttributes A nd C haracteristics of G rid R esources

Resource ID	No. of PE	MIPS of each PE	Total MIPS	price	Baud Rate
R1	2	10	20	100	1500
R2	12	10	120	150	1700
R3	3	13	39	300	1400
R4	8	15	120	210	1200
R5	3	20	60	90	1600
R6	6	12	72	250	1100

GridSim toolkit allows modeling and simulation of entities in parallel and distributed computing (PDC) systems-users, applications, resources, and resource brokers (schedulers) for design and evaluation of scheduling algorithms. It provides a comprehensive facility for creating different classes of heterogeneous resources that can be aggregated using resource brokers for solving compute and data intensive applications. A resource can be a single processor or multi-processor with shared or distributed memory and managed by time or space shared schedulers. The processing nodes within a resource can be heterogeneous in terms of processing capability, configuration, and availability. The resource brokers use scheduling algorithms or policies for mapping jobs to resources to optimize system or user objectives depending on their goals.

We modeled and simulated 6 time-shared resources. Each resource has a machine with different characteristics. Since the algorithm in [3] doesn’t consider the dynamic resource changing, there will be no such change in the simulation to enhance the comparability. The characteristics of resource are depicted in table 1. Each resource node has five properties—numbers of process element, processor capacity, price and bandwidth rate. Processor capacity can be expressed in million instructions per second (MIPS). The resource cost can be expressed in Grid dollars, which can be defined as the processing cost per MIPS. All of the parameters of the simulation environment are summarized in Table I. These experimental configurations are used to evaluate the performance of the resource scheduling algorithm as much as possible.

In our experiment, a user submits fine-grained jobs to the broker. And the job length is defined as 20MI (million instructions) with a random variation -d% to d%. We will test the performance of algorithm three times. In that process, d equal 30, 60 and 90 respectively. The length of input file is defined as 100 with a random variation -30% to 30%. The output file size of the grouped job is defined as 1000. The expected job processing time is defined as 15s. The overhead of job grouping is defined as 5s.

In the simulation, we performed scheduling experiments by setting different values to the number of jobs; the number of jobs is varied from 500 to 1000 in steps of 6. The executing time and cost is recorded to analyze the feasibility of our algorithm.

• B.    Experimental results

Simulations are conducted to analyze the executing time and cost of our algorithm. For all simulations we use the same set of default parameters which are given in the section A. In our experiments only the parameters d will be varied. Completion times and total cost are two measurement criteria to measure in the experiment. Completion times measure the time observed by the schedule to access the requested grid resources and complete the task. It is influenced by the available connections and bandwidth, and processor capacity, and processing delay. Cost is influenced by the price and the total length of fine-grained jobs. We recorded processing time and cost to demonstrate the validity of our algorithm. We make a conclusion that the whole system can reduce the processing time, and not to increase the total cost.

First experiment is to measure the effect of scheduling algorithm on completion times. Fig.5 shows the difference in jobs executing time between our algorithm and the DFJS algorithm [3] when d=30. Compared with the DFJS algorithm, our algorithm can reduce the executing time from 20 to 30s. This is because the Greedy algorithm used in AFJS algorithm can group the fine-grained jobs as much as possible. And that indicates a useful improvement especially when a deadline is engaged in.

Fig.6 and Fig.7 show the difference in jobs executing time between our algorithm and the DFJS algorithm [3] when d=60 and d=90 respectively. As is shown in the pictures, when d becomes lager, the jobs processing time of DFJS increased. But the jobs processing time of AFJS almost remains same. The AFJS algorithm could sufficiently utilize the capability of the resources since the grouped jobs match the MIPS of resource in a more proper way. Despite the variation of job length changed, the AFJS algorithm finish fine-grained jobs with same total length in the same time.

Fig.4 shows costs of the two algorithms. In our experiments, costs of the two algorithms are almost the same. It means AFJS didn’t increase the total cost compared with the DFJS algorithm. If we want decrease the total cost of the scheduling algorithm, some other algorithms can be introduced (e.g. cost-optimization scheduling algorithm) to decrease the total cost, but that case only happened when you pay more attention to the money rather than time.

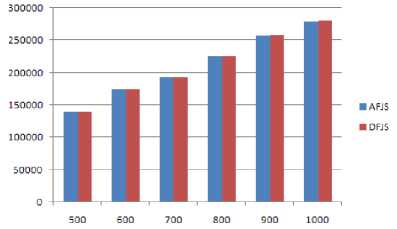
Figure 4. costs of the two algorithm(d=30)

All of the experiments are based on a static environment that can’t reflect the real world of grid computing. In grids, nodes which are carrying resources joining and leaving the network at any time, the available resources change dynamically over time. In experiments, none of resource properties is changed. Obviously, under conditions that status of resources changes, the job completion success rate of AFJS is higher than DFJS, because a mediator is adopted to obtain dynamic resource characteristics.

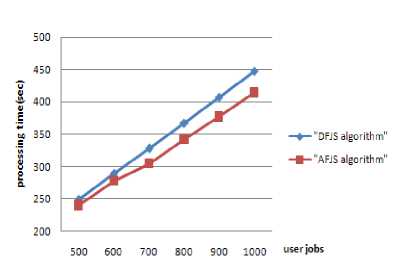
Figure 5. Jobs processing time (d=30).

• A.    Security

In grid computing, there are many security solutions [16, 21, 22, 24, 25]. Each one of these solution is explained in detail in their papers to provide insight as to their unique methods of accomplishing grid security. Any secure grid environment must employ mechanisms to secure authentication, authorization, data encryption, resource protection, and secure communication.

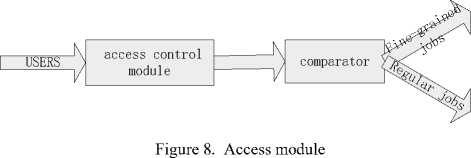
Like other grid environment, access control policy should be adopted in fine-grained job scheduling grid environment. In our system, a “ super scheduler ” must determine list of possible hosts if it has not already been defined, then must decide if a user is allowed to execute on those hosts. And to defend injection attack, the scheduler must also decide which user can submit the fine-grained jobs. We can adopt trust-based solution to decide which node is a secure one. Ref. [16, 24] provide two access control ways based on trust model.

In Fig.8, before jobs send to comparator the user should be authorized by access control module. If the trust degree of user is too low, the user can’t pass. All in all, the chief benefit of this system is that it merges security and resource management rather than pits them against each other.

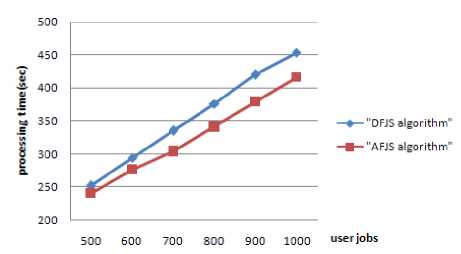
Figure 6. Jobs processing time (d=60)

• B.    Fault tolerant

If a malicious custom had been authorized, or a finegrained job had broken down, other security module or we can call it a fault tolerant mechanism should be added in our system.

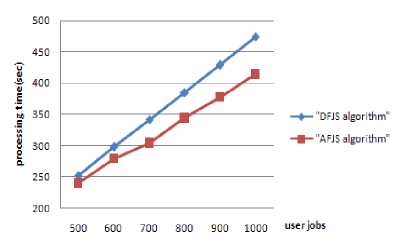
Figure 7. Jobs processing time (d=90)

• V.    Security and Fault Tolerant

In the system, sliding windows scheme is used to group fine-grained jobs. As we know, each coarsegrained job the scheduler submits to the resource is grouped by many fine-grained jobs. Each fine-grained job is stored in a sliding window. And a coarse-grained job is constituted by a group sequential sliding windows.

Fine-grained job i will break down in the following two cases: (1) a malicious custom was authorized by access control module accidentally; (2) some accidents happen in resource, just like electricity fails, the resource can’t obtain anymore. In the first case, though we can compute the next fine-grained jobs, the computing result is no longer worth trust. And in the second case, all the next fine-grained jobs have lost; we can’t obtain the computing results.

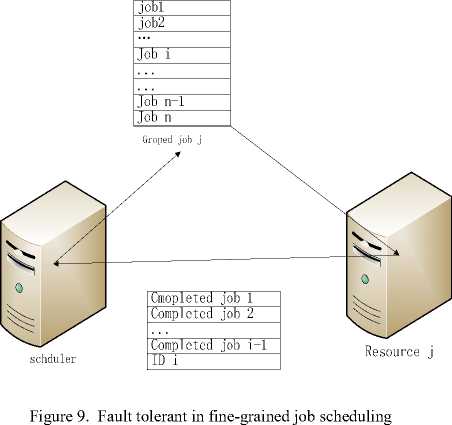
As is shown in Fig.9, if job i breaks down, all of finegrained jobs in the sliding windows behind it should be discarded. And the resource will submit the ID of job i and the computing result of the fine-grained jobs before job i to the scheduler. Then the scheduler will reschedule the fine-grained jobs behind job i , and analyze the finegrained job i , if it is a computer virus, the trust degree of the custom who submit it should be declined. If the failing execution of coarse-grained job is caused by resource, the job i will be rescheduled. Though we will reschedule all the fine-grained jobs behind the position i in sliding windows, this makes the system more security and fault tolerant. And from the scheduling algorithm, we know that the fine-grained job with lager MI always have a forward position in sliding windows. Then the reschedule jobs have a smaller MI, and they are easily grouped into another coarse-grained job.

• VI.    Conclusion

The purpose of this paper was to research fine-grained jobs scheduling in grid computing. Though there are many job scheduling algorithm in grid computing, little of them is concentrate on the fine-grained jobs scheduling. In order to utilize grid resources sufficiently, an adaptive fine-grain job scheduling algorithm is proposed. The grouping algorithm integrated Greedy algorithm and FCFS algorithm to improve the processing undertake of fine-grained jobs. The algorithm considers the dynamic characteristic of the grid environment. To protect the system from the injection attack, an access control module is engaged in. A fault tolerant mechanism is also used to process errors. Numeric experimental results demonstrate efficient and effective of our algorithm.

Though the proposed algorithm can reduce the executing time, its time complexity is higher than DFJS algorithm, and some improvement should be done in this aspect. Additionally, the simulation environment is semidynamic and it can’t reflect the real grid environment sufficiently. To further test and improve the algorithm and the system, some dynamic factors (e.g. local job with a higher priority) and inhibitory factors (e.g. network delay) will be taken into account. Also some experiments should be done under attack to test the reliability of the fault tolerant module.

Acknowledgment

The authors wish to thank the editors and the anonymous reviewers for their helpful comments and suggestions. The work is supported by National Natural Science Foundation of China (NSFC) under grants No.50675166 and 50620130441.