Research on the Quick Construction of the Edge-balance Index Sets of a Nested Graph with Infinite Paths and Power Circles
Автор: Hongjuan Tian, Yuge Zheng
Журнал: International Journal of Modern Education and Computer Science (IJMECS) @ijmecs
Статья в выпуске: 10 vol.4, 2012 года.
Бесплатный доступ
The research of Boolean index sets of graphs is one of the most important graph theories in the graph theory . Boolean index sets of graphs are to use the vertex sets and the edge sets of graphs to study the characteristics of various graphs and their inherent characteristics through corresponding the mapping function to Z_2. It’s theory can be applied to information engineering, communication networks, computer science, economic management, medicine, etc. The edge-balance index set is an important issue in Boolean index set. In this paper, we defined edge-friendly labeling of the graph, edge-balance index set of the graph and the graph {[C_(3^m)×P_(m_3)](m≥3)}. we completely determine the edge-balance index sets of the graph [C_(3^m)×P_(m_3)] for the integer [m≡3,0 (mod 4)] and solve formula proof and graphic tectonic methods.
Edge-friendly labeling, Edge-balance index set, Nested graph
Короткий адрес: https://sciup.org/15014495
IDR: 15014495
Текст научной статьи Research on the Quick Construction of the Edge-balance Index Sets of a Nested Graph with Infinite Paths and Power Circles
Binary labeling is a simplification of graceful labeling, introduced by Cahit[1]in his seminal paper on cordial graphs. Since then, other nation of balance in binary labeling([2]and[3] for example) have been introduced and much work has been done to classify graphs. So far, the problem is far from complete, though there are classification of index sets for specific graph classes (see [4]and[5] for example ).
Our objective is to assign a binary labeling to some substructure of graphs so that the assignment is balanced and induces a labeling on some other substructure. We then attempt to classify the degree of imbalance in the induced labeling of the graph. We hope that such an index set could form an invariant that in some way can distinguish classes of graphs. In this paper, we focus on the edge-balance index set of a class of nested network graphs.
For basic graph theoretic nation and definitions see Diestel [6]. All graphs G ( V , E ) are finite, simple, and undirected with vertex set V and edge set E . The number of vertices is denoted v ( G ) and the number of edges is denoted e ( G ) .
Let G(V, E) be a graph with vertex set V and edge set E . Integers set Z = {0,1} . Given an edge labeling functions f : E(G) ^ Z2. That is to say, Ve e E(G), f {e} =0 or 1. According to the edge labeling f, we define an associated partial vertex labeling f+ : V(G)^ Z2 as follow. Define f + (V) to be 0 if it is incident to more 0-edges than 1-edges and 1 if it is incident to more 1-edges than 0-edges, if the vertex v is incident to an equal number of 0-and 1-edges, leave it unlabeled. Hence f+ is a partial function. For each i e{0,1} , let ef (i ) = |{uv eE : f (uv ) = i} , and vf (i ) = |{v e V : f + (v ) = i} . If no ambiguity occurs, we could omit the subscript and simply write e(i) and v(i) respectively.
Definition 1.1 An edge labeling f: E(G)^{0,1}of the graph G is said to be edge-friendly if |e^ (0)- e^ (1) < 1
where e
-
( i ) is the cardinality of the set { e e E ( G ) : f ( e ) = i }
for i e { 0,1 } .[7]
Definition 1.2 The value |V/ (0) — V/ (1) is called on edgebalance index of G under an edge-friendly labeling f . The edge-balance index set of the graph G , denoted by EBI (G ), is defined as the set of all possible edge- balance indices of G . that is the set {V/. (0)- v^ (1) : f is an edge friendly labeling of G}.[7]
Specifically, the maximum of edge-balance index denoted by max { EBI ( g )}
The following construction of graph were considered in[8].
Definition 1.3 The graph is denoted by P , which is the nm paths which is m vertex in each path and every vertex has n bifurcates except the last vertex of path.
Definition 1.4 The graph is denoted by C , which is nm the m circle which is the inner circle containing n vertex and the vertex number of m circle from inside to outside successively increase by power exponent.
Definition 1.5 The sigh C m x P m denotes the power circles nested network graph by the power circles graph, C m , and the paths shape graph, P m .
We call an edge labeling of f ( xy ) is 1 to be 1-edge and an edge labeling of f ( xy ) is 0 to be 0-edge, the vertex labeling is 1 to be 1-vertex and the vertex labeling is 0 to be 0-vertex when the context is clear.
Example: The figure 1 gives several C^m x P m^
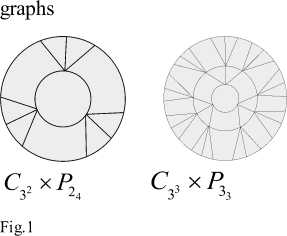
C 3 4 x P
For convenience, we will have the following label for the power circles nested graph :
The vertices of the inner circle in clockwise order were labeled as follows:
( I ) . . ( • ) =
( 1 ) . - I , ( . ).
, Similarly,
from inside to outside the vertices of the circle in clockwise were labeled as follows:
( m ) i . ( m ) 2 . ( m ) 3 . ( m ) 4... , ( m ) n m — I . ( m ) n m
Among them, symbols ( j ) says the i th vertex in the j th circle.
For the edge-friendly labeling of the graph C 3 m x P m ( m > 3 ) . Y stands for the total edges of the graph. We discuss the edge-balance index set of this graph from the following four parts:
m = 2 ( mod4 ) ; m = 3 ( mod4 ) ; m = 0 ( mod4 ) ;
m = 1 ( mod 4 ) . But. in this paper. we only research it when m = 3 ( mod4 ) and m = 0 ( mod4 ) . In the following we calculate EBI for the nested graph with infinite paths and power circle, using an approach which calculates the edge-balance indices by considering the existence of certain types of edge. First of all, we need the following lemma. Specifically, all the parameter is integer.
-
II. the edge-balance index sets of nested graph
C 3 m x P m 3 ( m = 3 ( mod4 ))
Lemma 1: For the graph C3 m x P^ for the integer m > 3 , when m = 3 ( mod4 )
max{ EBI ( C 3 m x P m 3)} = 3 m .
Proof: First, structure the graphics with the maximum edge - balance index:
Because the power circles nested graph were nested by the power circle graph and the paths shape graph. For convenience, we will label respectively the power circle graph and the paths shape graph.
In the paths shape graph, we mark all edges for 0-edge which are in the paths ( j - 2 ) a ( j - 1 ) b ( j ) c ( j + 1 ) d ( j + 2 ) e
' j = 4 k+1.2 < j < m;1 < a < 3j-2; b = 2 + 3 r .1 < b < 3j-1;'
c = 4 + r+9 s. r e{0.1.2} .1 < c < 3j; d = 10 + r + 27 s.
v 0 < r < 8.1 < d < 3 j + 1. e = 28 + r + 81 s .0 < r < 26.0 < e < 3 j + 2 ,
At the same time, the all edges in which ( j -1)b( j)C( j + 0d ( j + 2)e f j = 4k +1.2 < j < m;b = 1 + 3s.1 < b < 3j-1;
c = 3 + 9s.1 < c < 3j; d = 7 + r + 27s. r e {0.1.2}.
v 1 < d < 3 j + 1; e = 19 + r + 81 s .0 < r < 8.1 < e < 3 j + 2 ?
' j = 4 k +1.2 < j < m ; b = 3 + 3 r + 9 s . r e { 0.1 } .
( j - 1 ) b ( j ) c ( j + 1 ) d ( j + 2 ) e
1 < b < 3 j - 1; c = 7 + 9 r + 27 s . r e { 0.1 } .1 < c < 3 j ;
d = 19 + r + 27 s + 81 t . r e { 0.1.2 } . s e { 0.1 } .1 < d < 3 j + 1;
ve = 55+r+81 s+1271.0 (j) c (j+1) d (j+2) e 1 < c< 3j; d = 73 + 81 s .1 < d< 3j+1; ve = 217 + r+243s. r e{0.1.2} .1 < e< 3j+2? were marked as 0. And let the label of edges (j-1) b (j) c (j = 4 k+1,2 < j< m; b = 9+9 r ,1 < b< 3j-1;) (c = 26+27r ,1 < c < 3j; k, s eN were signed 0-edges. In addition, the edges (1)a (2)b (3)c (a e{1,2,3};b e{3,4,5,6,7} ;7 < c < 21) are the 0-edges, the other edges in the paths is labeled as 1. In the power circles graph, let the edges (j-1),( j-1)w (j-1)^2 (j = 4 k+1,2 < j < m;i = 1+3r ,1 < i < 3j-1) were signed 0-edges in the circle j-1(j = 4k+1,2< j< m). Let the edges were signed 0-edge except the edges (j )i (j )i+1(j = 4k +1,2 < j< m; i = 25 + 27r, 1 < i< 3j) in the circles j (j = 4k+1,2 < j< m). We mark all edges for 0-edge which are in the circles j+1(j = 4k+1,1 < j< m) . Let the edges ^j = 4 k+1,2 < j< m; i = 1+2 r+63 s+81u (j+2)i( j+2),1 vor220+2t+243u ,0< r< 8, s e{0,1}, t e{0,1,2} ,1 < i< 3j+2; ( 3)5 ( 3 +( 3 ( 3 ) 26 1 ( 3 ) 25 ( 3 )24 1 ( 3 )23 ( 3 ) 22 were also labeled as 0, the others edge in the circles is labeled as 1. In the graph, there are у = 3m+1— 6 edges, of which 3m+1 -7 are the 0-edges . According to the definition 2 of edge-friendly labeling, | e(0) — e(1) |< 1, we can get the edge-friendly labeling of the labeled graph by calculation. In this labeled graph, all the vertices j = 4 k+1,1 < j< m; Ii = 2+3t ,1 < i< 3 j—1J ,(j )i ^ j = 4 k+1,1 < j< m; 4 i = 3+s+91,0 < s < 4,1 < i < (j)(j = 4 k +1,1 < j < m; i = 21 + s + 27t ,0 < s < 3,1 < i < 3j), (j + 1)3ir( j = 4 k+1,1 < j < m; i = 3+s+9t ,0 < s < 4,1 < i < 3j+1), (j+1)зД j = 4 k+1,1 < j < m; i = 21+s+27t ,0 < s < 3,1 < i < 3j+1), (j +1)( j = 4 k +1,1 < j < m; i = 73+81t ,1 < i < 3 j+1) are 0-vertex. In addition, the vertices (1)2,(2) (i = 3,---,7) are also 0-vertex, others are 1-vertex. Thus, we can gain m v (0 ) = 3-3 . Due to V (G ) = 3 (3m—1) vertices in this graph which is defined by the f+, one of the vertices is not defined, then v(1) = 5X3-3 . After this |v(0)-v(1)| = 3m. We can prove EBI(C^m X p) = 3m is the maximum of edge-balance index in the graph C^m X p (m > 3) . In this labeled graph, the vertices of the outside circle have 3 adjacent edge, and the edges adjacent to the vertices of the inner circle are 5, the edges next to the vertices of others circles are 6. The degree of all 0-vertex is six. Others vertices with six degree except one is unlabeled is 1-vertices. All the vertices with five and three degree is 1-vertices. What’s more, the adjacent edges with 0-vertex is 0-edge, the adjacent edge with 1-vertex whose degree is six and five is two, the adjacent edges with 1-vertex whose degree is three is only one. When we change the 0-vertex into 1-vertex or unlabeled vertex, we must take out three 0-edges. Thus, we exchange one 0-edge and 1-edge at random, the difference value of v (0) and v (1) must decrease. So the difference value is maximum, that’s to say: max{EBI(C3m x?m3)} = 3m. Lemma 2: In the graph Cm x p^ for the integers m > 3 , when me3(mod4),{3m - 1,...,1,0}CEBI(Cm xPm3). Proof: In the lemma 1, when m = 3 (mod 4) , we get max{EBI(C3m x Pm3)} = 3m. Below transform is based on the biggest index labeled graph constructed form lemma 1, and every step all proceeds is based on the previous step to transform, which in turn constructs labeling graphs corresponding with the index. Among the (2k - 1)r(2k)^ ^ (2k)5(2k)s+1means that we exchange (2k -1)^(2k)s and (2k)Д2k)5+1 which are 0-edge and 1-edge respectively. First, build an even index set: Step 1: Exchange (1) (1)2^ (1)] (2),, we can obtain the edge-balance indexes which is ^(0)-v(1)|= 3m -1. Step 2: In turn exchange (2)1 (2)2 ^(2)1 (3)3 , (2), (2)9 ^(2)8 (3)24 and (2 )9( 2 ^o( 2 )9( 2 )27 , we can obtain 3 labeled graphs of even edge-balance indexes which are {3m - 3,3m - 5,3m - 7} . Step 3: In turn exchange (2)a(3).«(3).(3)b-.(a-W;b =7-r-37 '•},72b221) - we can obtain 10 labeled graphs of even edgebalance indexes which are {3m -9,- • *,3m -27}■ Step 4 : In turn exchange (j-1).(j- 2). «(j- 2).(j- 2).-1 ' j = 4 k -1,12 j 2 m; a = 7 - 5 - 27t - 81« ,12 a 2 3j-1; b = 19 - r' ^-3 s - 81t - 243u, r e{0,1} ,12 b 23j-2;02s214, t e{0,1} , we can obtain these labeled graphs of even edge-balance indexes which are Step 5: In turn exchange ( j -1).( j - 2). «( j - 2).(j- 2) b-1 ^j = 4 k -1,12 j 2 m; a = 61 - s - 81u ,12 a 2 3j-1; чb = 181 - r - 3 s - 243u, r e{0,1} ,12 b 2 32,0 2 s 214 , we can obtain these labeled graphs of even edge-balance indexes which are J 1(3m -27)-2,---, —(3m -29)|. I2V ' 60V Step 6: In turn exchange (j-1) a(j-1) a-1 «(j-1) a(j- 2) b ' j = 4k -1,12 j 2 m; a = 1 - r - 21 s - 27t,12 a 2 3j-1;' vb = 3-3r-64s-81t,12 b 2 3j-2,0 2 r 2 4,s e{0,1}? we can obtain these labeled graphs of even edge-balance indexes which are J1670 (3■ -27)-2,—,310 (3 • -27)} ■ Step 7: In turn exchange ( j -1) a( j -1) a-1 «( j -1) a( j - 2) b ^ j = 4k -1,12 j 2 m; a = 74 - r - 81 s,12 a 2 3j-1; v b = 222 - r - 243s ,12 b 2 3 j-2; r e{0,1} , we can obtain these labeled graphs of even edge-balance indexes which are J — (3m -27)-2,---, —(3m -29)I■ [30v 7 60v 7 J Step 8: In turn exchange (j - 2) b(j - 2) b-1 «(j - 2) b(j - 2) b-1 (j = 4 k -1,12 j 2 m; b = 220 - 243r ,12 b 2 3j-2) we can obtain these labeled graphs of even edge-balance indexes which are J—(3m -29)-2-•••-—(3m -2?)I■ I60v ’ 120v 7I Step 9: In turn exchange ( j - 2) b( j - 2) b-1 «( j - 2) b+1( j - 2) b +2 (j = 4k -1,12 j 2 m; b = 224 - 243r, 12 b 2 3j-2) we can obtain these labeled graphs of even edge-balance indexes which are J — (3m -27)-2-•••-2-01 ■ [120v 7 J Odd index collection structures as follows: Step 1: In turn exchange ( 2)1 ( 2)2 «( 2)1 ( 3)э , (2)8 (2)» «(2)8 (3)24 and (2 )9( 2 )«(2 )9(2 )27, we can obtain 3 labeled graphs of odd edge-balance indexes which are {3m - 2,3m - 4,3m - 6} . Step 2: In turn exchange ( 2)a (3)b «(3)b (3)b-. (a ={3-•••-?};b = 7-r-3s,r e{0,1),7 2b 2 21), we can obtain 10 labeled graphs of odd edgebalance indexes which are {3m - 8,---,3m - 26} ■ Repeat the fourth, fifth, sixth, seventh, eighth, ninth step when the even index set were structured, we can obtain these labeled graphs of odd edge-balance indexes which are respectively {3m - 28,- • *,3,1} . In conclusion, we can prove {3m -1,3m -2,-..,1,0} c EBI(C3m xPm3). III. the edge-balance index sets of nested graph C3mxPm3 ( m = 0( mod4)) Lemma 3: For the graph C3m x p^ (m > 3) , when m = 0(mod4) max{EBI(C3m x Pm )} = 3m. Proof: First, structure the graphics with the maximum edge - balance index: Because the power circles nested graph were nested by the power circle graph and the paths shape graph. For convenience, we will label respectively the power circle graph and the paths shape graph. In the paths shape graph, we mark all edges for 0-edge which are in the paths ( j - 2) a( j - 1) b( j ) c( j -1) d( j - 2) e ' j = 4k+2,3 2 j 2 m;12 a 2 3j-2;b = 2 -3r,12 b< 3j-1; ' c = 4-r-9s,r e {0,1,2},12 c 2 3j;d = 10-r-27s, 40 2 r 2 8,12 d 2 3j-1; e = 28 - r - 81 s,0 2 r 2 26,0 2 e 2 3j-2? At the same time, the all edges in which (j-1) b(j ) c(j+1) d(j+ 2) e 2 j = 4k + 2,3 < j< m;b = 1 + 3s,1 < b< 3j-1; c = 3 + 9s,1 < c< 3j;d = 7 + r + 27s,r e {0,1,2}, (1 < d< 3j+1; e = 19 + r + 81 s,0 < r< 8,1 < e< 3j+2J (j -1) ь (j ) c( j +1) d(J+ 2) e 'j = 4k+2,3<j<m;b = 3+3r+9s,r e{0,1),1 <b<3j-1;c = 7+9r ' +27 s, r e{0,1} ,1 < c < 3j; d = 19+r+27 s+81/, r e{0,1,2}, s e{0,1}, J < d < 3j+1; e = 55 + r+81 s +127 t ,0 < r < 8, s e{0,1} ,1 < e < 3j+2 , and ( j ) c( j +1) d( j + 2) e 2 j = 4k+2,3 < j< m;c = 25 + 27s, 1 < c< 3j; d = 73 + 81 s,1 < d< 3j+1; (e = 217 + r + 243s,r e {0,1,2} ,1 < e < 3j+2, were marked as 0. And let the label of edges (j -1) b(j) c 2j = 4k+2,3 < j< m;b = 9 + 9r, 2 (1 < b < 3j-1; c = 26 + 27r,1 < c < 3j J were signed 0-edges. In addition, the edges (1)o (2)b (3)( (a e {1,2,3};b e {3,4,5,6,7};7 < c< 21) and (1)1 (2)2, (1)1 (2),. (1)2 (2),-(1)2 (2M1), (2),•(!), (2), are the 0-edges, the others edges in the paths is labeled as 1. In the power circles graph, let the edges (j-1) i (j -1) i+1 (j-1)i+2 (j=4 k+2,3 < j< m; i = 1+3r ,1 < i< 3j-1) were signed 0-edges in the circle j -1( j = 4k+2,3 < j< m). Let the edges were signed 0-edge except the edges (j )i (j ),+i (j = 4 k+2,3 < j< m; i = 25+27r, 1 < i< 3j) in the circle j (j = 4k+2,3 < j < m). We mark all edges for 0-edge which are in the circles j+1( j = 4k+2,1 < j < m) . Let the edges edges (2 ), (2 )1- ( 2 ). ( 2 ), in the second circle. The edges (4)i(4)i.1(i = 1 + 2r,1 <i< 5) and (4), (4LCi = 81 - 2r,52 < i< 81) were also labeled as 0, the others edge in the circles is labeled as 1. In the graph, there are у = 3m+1- 6 edges, of which 3m+1 - 7 is the 0-edge. According to the definition of edge-friendly labeling, | e(0) - e(1) |< 1, we can get the edge-friendly labeling of the labeled graph by calculation. In this labeled graph, all the vertices (j -1) _ (j = 4 k + 2,1 < j < m; i = 2 + 3t ,1 < i < 3j-1), (j)(j = 4 k+2,1 < j< m; i = 3+s+9t, s e{0,1,2.3,4} ,1 < i< 3j), (j)(j = 4 k + 2,1 < j< m; i = 21 + s + 271, s e{0,1,2,3} ,1 < i< 3j), 2 j = 4k + 2,1 < j< m; i = 3 + s + 9t,л (s e{0,1,2,3,4} ,1 < i< 3j+1 ? , (j +1) 2 j = 4k + 2,1 < j< m; i = 21 + s + 271,2 (s e {0,1,2,3} ,1 < i< 3j+1 v (j +1)( j = 4 k + 2,1 < j< m; i = 73 + 81t ,1 < i< 3j+1) are 0-vertex. In addition, the vertices ( 2 )(i = 1,2,3,4 ),( 3\( i = 3,4,--.,15 ) are also 0-vertex. The others are 1-vertexs. Thus, we can , . 3m - 3 gain v ( 0) =------- . Due to V(G) = ^(3 -1) vertices in this graph which is defined by the f+ , one of the vertices is not . _ . . 5 x 3m - 3 . defined ,then v(1) =-----------. After this (j+2)i( j+2)i+1 j = 4 k+2,3 < j< m; i = 1 + 2 r + 63 s+81u or220 + 2/ + 243u, 0 < r< 8, s e {0,1}, v/ e {0,1,2} ,1 < i< 3j+2 у Iv(0)-v (1)1 = 5 x 3m - 3 3m - 3 - 3m. were signed 0-edge in the circle j+2(j = 4k+2,3 < j< m). In addition, let the edges were signed 0-edges except the we can prove EBI(C3W x pз) = 3m is the maximum of edge-balance index in the graph Cm x Pm (m = 0 (mod 4)). In this labeled graph, the vertices of the outside circle have 3 adjacent edges, and the edges adjacent to the vertices of the inner circle are 5, the edges next to the vertices of others circles are 6. The degree of all 0-vertex is six. Others vertices with six degree except one is unlabeled is 1-vertices. All the vertices with five and three degree are 1-vertices. What’s more, the adjacentedges with 0-vertex is 0-edge, the adjacent edge with 1-vertex whose degree is six and five is two, the adjacentedges with 1-vertex whose degree is three is only one. When we change the 0-vertex into 1-vertex or unlabeled vertex, we must take out three 0-edges. Thus, we exchange one 0-edge and 1-edge at random, the difference value of v (0) and v (1) must decrease. So the difference value is maximum, that’s to say: max{EBI(C3„ xp)} = 3m. Lemma 4: In the graph C x P (m > 3) , when m = 0(mod4) , {3m -1,3m -2,---,2,1,0} c EBI (C3 m x Pm) Proof: In the lemma 3, when m = 0 (mod 4) , we get max{EBI(Cm x Pm3)} = 3m. Below transform is based on the biggest index labeled graph constructed form lemma 5, and every step all proceeds is based on the previous step to transform, which in turn constructs labeling graphs corresponding with the index. Among the (2k - 1)Д2k)5° (2k)Д2k)5+1 means that we exchange (2 k - 1)r(2 k )s and (2 k )Д2 k )s+1 which are 0-edge and 1-edge respectively. First, build an even index set: Step 1 Exchange (1) ( 2)2°(1)(2), we can obtain v (0) - v (1)| = 3m-1. Step 2: Exchange(3) (3)2° (3) (4)t, we can obtain v (0)- v (1) = 3m - 3. Step 3: In turn exchange ( 3) a ( 3) a+1 °( 3) a ( 4) b (» = 18 +Г;Ь = 52 + 3Г, Г Ф1,-,8}) , we can obtain 10 labeled graphs of odd edgebalance indexes which are {3m -5,3m -7,3m -9,-,3m -19,3m -21}. Step 4: In turn exchange . x , . ( X ( X fa = 3+r; b = 7 + r+3 s, ) (3)a(4)b ° (4)b (4)b+1 ^re{0,1}, s e{0,1,2, - • • ,14}J ’ we can obtain 10 labeled graphs of odd edgebalance indexes which are {3m -23,3m -25,---,3m -59,3m -81}. Step 5: In turn exchange ( j+1) g ( j+ 2) ь °(j+ 2) ь(j+ 2) ь+, ' j = 4 k+2,1 < j< m; a = 7+s+271+81u ,1 < a< 3j+1; b = 19+r ^, +3 s+81t+243и, r e{0,1} ,1 < b< 3j+2; s e{0,1,-,14}, t e{0,1}? we can obtain these labeled graphs of even edge-balance indexes which are Step 6: In turn exchange ( j +1) a( j + 2)b °( j + 2)b( j + 2) b+1 fj = 4 k+2,1 < j < m; a = 61+s+81и ,1 < a < 3j+1; , v b = 181+r+3 s + 243u, r e{0,1} ,1 < b < 3j+2; s e{0,1,-,14}v we can obtain these labeled graphs of even edge-balance indexes which are J 1(3m -81)-2,..., 17(3m -81)I. L 2V ’ 60v 7J Step 7: In turn exchange ( j +1)a( j +1)a+1 °(j+1)a( j + 2) b (j = 4 k+2,1 < j< m; a = 1+r+21 s+271,1 < a< 3j+l; ) V b = 3+3 r+64 s+81t ,1 < b < 3 j+2; r e{0,1,2,3,4}, s e{0,1}v we can obtain these labeled graphs of even edge-balance indexes which are J—(3m - 81) - 2,--, — (3m - 81) I. L60' 1 , ’30v Step 8: In turn exchange ( j + 1)a( j + 1)a+1 °( j + 1)a( j + 2) b " j = 4k + 2,1 < j < m; a = 74 + r + 81 s,1 < a < 3j+1;" 4 b = 222 + r + 243s ,1 < b < 3j2; r e{0,1} we can obtain these labeled graphs of even edge-balance indexes which are J — (3m -81)-2,..., —(3m -81)I. L30v 7 607 Step 9: In turn exchange / X X Z X Z X f j = 4k + 2,1 < j< m; (j+2).(j+2). . °(j+2).(j+2). I V jbV )b+1 V )bV b--1(b = 220+243r ,1 < b< 3 j+2 we can obtain these labeled graphs of even edge-balance indexes which are J Х(зm -81)-2,..., —(3m -81) 1. L 60v 7 , ’120v 7J Step 10: In turn exchange (j + 2) b (j + 2) b+1 °(j + 2) b+1 (j + 2) b +2 we can obtain these labeled graphs of even edge-balance indexes which are J — (3m -81)-2,---,2,0 1 I120V 7 J j = 4 k+2,1 < j < m; b = 224+243r ,1 < b< 3j+2 Odd index collection structures as follows: Step 1: Exchange (3)1 (3)2 «(3), (4),, we can obtain the edge-balance indexes which is |v(0)-v(1)| = 3m -2. Step 2: In turn exchange (3! .(3).„,«( 3).(4) J" =184r;b = 52■3r,r ef».1.-.8}) we can obtain 9 labeled graphs of odd edgebalance indexes which are {3m -4.3m -6,3m -8,—,3m -18,3m -2»} . Step 3: In turn exchange
(3). (4)b ~(4)b (4)ь.
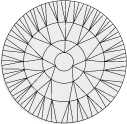
(. = 3 + r; b = 7 + r + 3 s, r e {0.1}, s e {0,1,2, •••,14}). we can obtain 30 labeled graphs of odd edgebalance indexes which are {3m - 22,3m - 24, • • • ,3m - 56,3m - 58,3m - 60} . Repeat the fifth, sixth, seventh, eighth, ninth, tenth step when the even index set were structured, we can obtain these labeled graphs of odd edge-balance indexes which are respectively {3m -62,3m -64,3m -66,---,7,5,3,1}. In conclusion, we can prove {3m -1,3m -2,...,2,1,0} о EBI(C3m XPm3). IV. CONCLUSION According to lemma 1,2 and lemma 3,4, we can get the following theorem: Theorem 1: In the graph Cgm x P^ for the integers m > 3 , m = 3,0(mod4) , EBI(Cm xPB))= {3m,--,1,0} Acknowledgment Thanks for project supported by the Innovating Foundation of Henan Polytechnic University for the Master Thesis. Thanks for project supported by Applied Mathematics Provincial-level Key Discipline of Henan Province and Operational Research and Cybernetics Key Discipline of Henan Polytechnic University. Thanks for project supported by the Ph.D. Foundation of Henan Polytechnic University Grant No.B2011-085.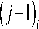

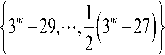
Список литературы Research on the Quick Construction of the Edge-balance Index Sets of a Nested Graph with Infinite Paths and Power Circles
- S-M. Lee, A LIU, and S K Tan, On balanced graphs, Cong. Numer, 87(1992),pp.59-64.
- M.K and S-M Lee, on edge-balanced graphs, Graph Theory, Combinatories and Algorithms, 1(1995),711-722.
- B.L.Chen, K.C. Huang and Shi-Shen Liu, On edge-balanced multigraphs, Journal of Combinatorial Mathematics and Combinatorial Computing, 42 (2002), 177-185.
- D.Chopra, S-M Lee and H.H.Su, On edge-balanced index sets of wheels, Int.J.Contemp.Math.Sciences, 5(2010), no.53,2605-2620.
- R.Diestel, Graph theory, Third Edition, Springer-Verlag, Heidelberg Graduate Texts in Mathematics,vol 173,2005.
- Yuge Zheng, Juan Lu, S-M Lee and Ying Wang, On the perfect index sets of the chain-sum graphs of the first kind of K4-e, 2009 2nd International Conference on Intelligent Computing Technology and Autination, v4, 586-589, 2009.
- Yuge Zheng, Hongjuan Tian, On the edge-balance index sets of the power circle nested graph {[C_(2^m)×P_(m_2)][m≡0 (mod 2)]}, Advanced Science Letters, vol 7(2012),534-536.


