Решение для фундаментальной моды ступенчатого оптического волоконного волновода с керровской нелинейностью

Прогресс в области создания волоконных фемтосекундных лазеров и их приложений [1-6] делает крайне актуальной задачу моделирования процессов распространения в оптических волоконных волноводах ультракоротких импульсов большой мощности. Уже сегодня с помощью таких лазеров получены импульсы длительностью менее 30 фемтосекунд с пиковой мощностью до 81 ГВт и энергией 2,6 МДж [1-3]. При таких значениях пиковой мощности нельзя не учитывать зависимости параметров мод оптического волновода от нелинейности [7-8].

Для световодов из плавленого кварцевого стекла можно полагать, что при фемтосекундных длительностях импульсов можно ограничиться учетом только нелинейности Керра [9-10]. При этом условии в [11] методом приближения Гаусса [12-14] было получено аналитическое решение для фундаментальной моды кварцевого ступенчатого оптического волокна с учетом влияния керровской нелинейности. Однако авторы [11] полагали, что мощность достаточно мала, чтобы пренебречь составляющими, включающими оптическую мощность во второй степени. Следует ожидать, что при значениях пиковой мощности порядка десятков мегаватт это недопустимо.

В данной работе рассмотрено решение для фундаментальной моды ступенчатого оптического волоконного волновода из кварцевого стекла, учитывающее все составляющие зависимости показателя преломления материала от пиковой мощности оптического излучения вследствие нелинейности Керра. Представлены результаты анализа зависимостей радиуса пятна и постоянной распространения фундаментальной моды такого волновода от пиковой мощности оптического излучения, обусловленных керровской нелинейностью.

Постоянная распространения фундаментальной моды кварцевого ступенчатого оптического волновода с керровской нелинейностью

При выводе выражения для постоянной распространения фундаментальной моды ступенчатого волоконного световода с керровской нелинейностью как в [11] воспользуемся методом приближения Гаусса [12-14]. В частности, используем представленную в [14] форму записи общей формулы для постоянной распространения некоторой моды заданных азимутального и радиального порядков круглого оптического волновода с произвольным профилем показателя преломления:

Р” = R2«2wfe°w]2^—(1) о                      a"Rg x = (R/ К0У ; R = r/ а; Ro = г0/ а,   (2)

где β – постоянная распространения моды; к = Тл / X – постоянная распространения в свободном пространстве; λ – длина волны; n – показатель преломления материала оптического волокна; a – радиус сердцевины оптического волокна; r ₀ – эквивалентный радиус пятна моды; F^P (х) – функция радиального распределения поля моды азимутального порядка l и радиального порядка m по сечению оптического волокна; C_l,m – константа, определяемая в зависимости от азимутального порядка и радиального порядка моды; r – радиальная координата.

С учетом вклада нелинейности Керра распределение показателя преломления вдоль радиуса ступенчатого оптического волокна описывается формулой [7]:

n_N(R) = n_s + п₂I(R),          (3)

где n ₂ – параметр керровской нелинейности, мкм ² /Вт; I ( R ) – распределение интенсивности оптического излучения вдоль радиуса волокна; n_s ( R ) – профиль показателя преломления ступенчатого оптического волокна без учета нелинейности, который, согласно [12], описывается соотношением:

ns№

пс ,R<1; nd,R>V

Предполагается, что распределение интенсивности оптического излучения в волоконном световоде имеет осевую симметрию и согласно приближению Гаусса [12] распределение фундаментальной моды по сечению волоконного световода описывается с учетом (2) как

F,P4x) = exp(-x/2).         (5)

Тогда, согласно (2)-(5), если в ступенчатом оптическом волокне распространяется только фундаментальная мода, то его профиль показателя преломления может быть представлен как:

n_N (л) = n_s (R) + и₂              ,     (6)

Tia 2R0

где Pm – пиковая оптическая мощность. Здесь учитывали, что радиус пятна моды волоконного световода в два раза больше его эквивалентного значения по аппроксимации Гаусса [15]. Подставляя (5) и (6) в (1), получаем:

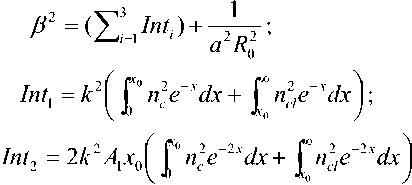
Int₃ = A^y^Xg I e ^3xdx ;

4 ^{= n}i P_m / 2^a²; x₀ = 1 / R³.

Интегрируя (7) согласно [16-18], получаем выражение для постоянной распространения фундаментальной моды в ступенчатом оптическом волокне с учетом нелинейности Керра:

P" = к2н3 —k^NA’e '° —k^^nA^Xg e 23|J +

+ k³n A x -vk^A^x¹ /3 —x (a¹           (8)

В отличие от решения, представленного в [11], выражение (8) включает все составляющие показателя преломления материала, обусловленные нелинейностью Керра.

Характеристическое уравнение относительно эквивалентного радиуса пятна фундаментальной моды кварцевого ступенчатого оптического волновода с керровской нелинейностью

Согласно методу приближения Гаусса [12] уравнение относительно эквивалентного радиуса пятна моды получаем, дифференцируя выражение для постоянной распространения моды по эквивалентному радиусу пятна моды и приравнивая эту производную к нулю, что эквивалентно уравнению z^ = o . Дифференцируя (8) по х ₀ и

5x0                                     0

приравнивая полученную производную к нулю, получаем следующее характеристическое уравнение:

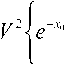
NA2

[az?(2x₀ -l)e ^2a°

-n

XApxp 3NA2

V² = k²a²NA², NA" = n² - up , A/z = n_c - n_cl.

В отличие от известного решения, представленного в [11], уравнение (9) учитывает все со- ставляющие показателя преломления материала, обусловленные нелинейностью Керра.

Анализ влияния керровской нелинейности на радиус пятна фундаментальной моды ступенчатого оптического волновода

В целях оценивания зависимости эквивалентного радиуса пятна от пиковой мощности оптического излучения были рассмотрены примеры волоконного оптического волновода с диаметром сердцевины 2,0 мкм (см. пример №1); 4,15 мкм (пример №2) и 8,0 мкм (пример №3). Значения показателя преломления материала сердцевины и оболочки, параметра керровской нелинейности были заданы как для стандартного ступенчатого оптического волокна SMF-28 [19]. Для примера №1 расчеты были выполнены на длине волны 800 нм, а для примеров №2 и №3 на длине волны 1550 нм. Соответственно, в примере №2 рассмотрено оптическое волокно типа SMF-28 с учетом керровской нелинейности на длине волны 1550 нм.

На рис. 1 приведены результаты решения уравнения (8) для примера №1, а на рис. 2 – для примеров №2 и №3. Анализ уравнения (9) и результатов вычислений показал, что, как и ожидалось, вследствие нелинейности Керра с увеличением мощности оптического излучения радиус пятна моды уменьшается. В зависимости от величины «₂^Рт ^Пс / ^ можно выделить три области решения уравнения (9). При значениях этой величины до 0,8 - 0,9 существует только одно решение уравнения. При значениях более 0,9 появляется второе решение. Однако уже при и₂ Р„, п_с /2^1 уравнение (9) не имеет решений. Вопрос о физическом смысле второго решения характеристического уравнения выходит за рамки статьи и здесь не рассматривается.

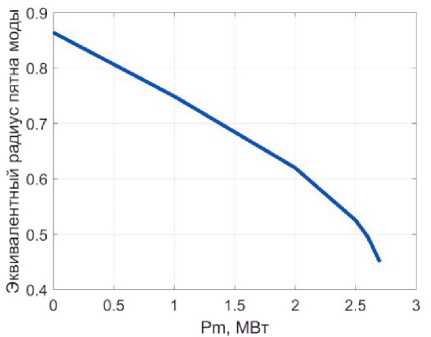
Рис. 1. Результаты решения уравнения (8) для примера №1

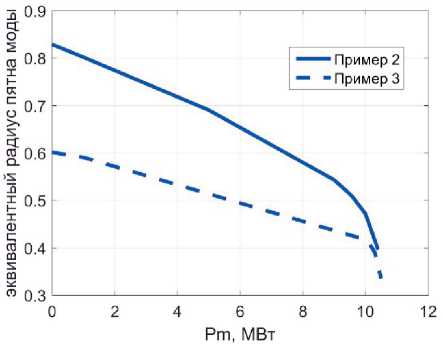
Рис. 2. Результаты решения уравнения (8) для примеров №2 и №3

Анализ влияния керровской нелинейности на постоянную распространения фундаментальной моды ступенчатого оптического волновода

На рис. 3 и рис. 4 приведены результаты вычислений зависимостей постоянной распространения фундаментальной моды от пиковой мощности в ступенчатом оптическом волокне с керровской нелинейностью по формулам (8 - 9).

Анализ полученных зависимостей показал, что они с высокой степенью точности могут быть аппроксимированы полиномами второй степени. В таблице 1 приведены значения коэффициентов аппроксимации и оценки максимальной погрешности такой аппроксимации для рассмотренных примеров. Во всех рассмотренных случаях погрешность не превысила 0,01%.

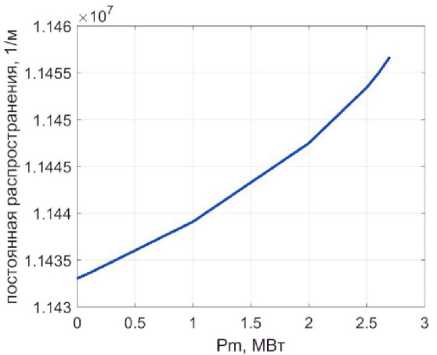
Рис. 3. Зависимость постоянной распространения фундаментальной моды от мощности оптического излучения для примера №1

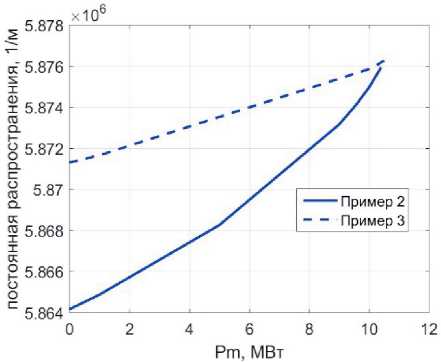
Рис. 4. Зависимость постоянной распространения фундаментальной моды от мощности оптического излучения для примеров №2 и №3

Заключение

В работе представлен вывод выражения для фундаментальной моды кварцевого ступенчатого волоконного световода с керровской нелинейностью и характеристического уравнения для нее. В отличие от известных решений представленное в данной работе учитывает все составляющие показателя преломления материала, обусловленные нелинейностью Керра.

Таблица 1. Значения коэффициентов аппроксимации и оценки максимальной погрешности

Номер примера	/?-Ю~6 = а+ЪРт+сР;			^ max, %
	а	b	С
1	11,43	3,9-10"3	1,74-10"3	0,004
2	5,86	0,5-10"3	5,78-10"5	0,006
3	5,87	0,3-10"3	1,57-10"5	0,001

Для ряда примеров приведены результаты вычислений зависимостей эквивалентного радиуса пятна моды и постоянной распространения моды от мощности оптического излучения при условии распространения в световоде только фундаментальной моды.

Показано, что в этом случае с погрешностью менее 0,1% зависимость постоянной распространения фундаментальной моды от мощности оптического излучения может быть аппроксимирована полиномом второй степени. Для рассмотренных примеров волоконных волноводов из кварцевого стекла получены значения коэффициентов аппроксимации. Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-60015 мол_а_дк.