Решение и уравнения пузырькового потока

Zuber) Они предполагали, что господствующий механизм теплообмена -теплопроводность. (Плезет и Цвик) Они предполагали единичный сопротивление теплообмена, обеспеченное тонким жидким оболочка окружающим пузырь.

Решение уравнения роста пузыря может быть упрощено, рассматривая последовательность трех режимов пузыря:

-поверхностное напряжение управляла стадией, где пузырь растет от критического радиуса (зарождение, нуклеация). Самый маленький пузырь, способный к росту имеет радиус:

2ст

Р -Р sat s

-инерция управляла стадией, где пузырь растет по постоянной норме, определенной давлением пара и плотностью перегретой жидкости. Этот процесс имеет место очень быстро (в порядке микросекунд) и заключительный радиус пузыря - приблизительно в 10 раз ri: Г2 * 10.Г dR dt

2(Pb - P) 3Pl

асимптотическая стадия, где пузырь растет, ограничена теплообмена, и следует Плезет и Цвик отношение или другая корреляция

Уравнение Плезет и Цвик

R

0.5

R0 Г« пц V 3t)

Г з )0.5 k (To - Tb)  1

V п )     L p D 0.5 1 0.5

В работе предложено отношение для роста пузыря, которое для асимптотических случаев «медленного и быстрого роста пузыря.

dR m= dτ

m

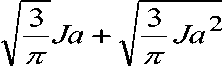
+ 2 Ja

J a =

ρ ′ C_p Δ T

ρ′′L

R п = R kp

dR

+- — d τ

4 3 m_п = πρ ₂ Rп

4Γ3′2 + Γ3′′2 = N  π.Rп ρ2

где р'- плотность жидкости; р”- плотность пара; AT=T^-Ts “жидкость на бесконечности - поверхность пузырька ”; Ср- удельная теплоемкость жидкости при постоянном давлении; L- теплота фазового перехода; R-радиус пузыря; т- время; а- теплопроводность.