Решение игры с природой с нечеткими лингвистическими параметрами
Бесплатный доступ
Рассматривается ситуация, требующая принятия решения, формализуемая как игра с природой. Для учета возможных неопределенностей в оценке исходных параметров игры вероятности проявления тех или иных состояний природы и элементов платежной матрицы предлагается их представление в виде нечетких, лингвистических утверждений без ограничений на вид функций принадлежности соответствующих нечетких множеств. Учет влияния возможных состояний природы предлагается осуществить через изменение истинности нечетких оценок последствий возможных решений (элементов платежной матрицы). Выбор наилучшей стратегии основывается на интегральной оценке последствий возможного решения по всему пространству состояний природы, получаемой в виде эквивалентного нечеткого множества с треугольной функцией принадлежности с последующим вычислением отношения координаты центра тяжести этого множества к уровню его размытости. Значение этого отношения характеризует уровень соответствия имеющихся вариантов решений предположению о предпочтительности.
Игра с природой, платежная матрица, нечеткое множество, лингвистическое значение, функция принадлежности
Короткий адрес: https://sciup.org/148330361
IDR: 148330361 | УДК: 519.816 | DOI: 10.18137/RNU.V9187.24.04.P.44
Текст научной статьи Решение игры с природой с нечеткими лингвистическими параметрами
Среди задач исследования операций можно отметить два вида, которые имеют определенные сходства в формулировании исходных условий. Первый – это так называемые игры с природой, которые задаются следующим набором:
A= {ai :i=1,N} - множество стратегий рационального участника ситуации, требующей принятия решений;
S= {Sj:j=1,M} - множество объективных условий, в которых приходится принимать решения (состояния природы);
Решение игры с природой с нечеткими лингвистическими параметрами
Чернов Владимир Георгиевич доктор экономических наук, профессор, профессор кафедры вычислительной техники и систем управления, Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, город Владимир. Сфера научных интересов: исследование операций, модели и методы поддержки принятия решений в условиях нестатистической неопределенности, прикладные нечеткие системы. Автор более 150 опубликованных научных работ. ORCID:0000-0003-1830-2261, SPIN-код: 2123-9670, AuthorID:16400.
распределение вероятностей на S –
P(S)= { p(S j ):j=1M ) ; (1)
распределение оценок последствий выбора стратегии V a i е A при j -м состоянии природы (платежная или оценочная матрица) –
G= { g ij :i=1N,j=1M } . (2)
Второй вид – это антагонистическая игра, предложенная Дж. Харшаньи [1], в которой предполагается, что каждый из участников формирует так называемый тип другого игрока в виде распределения вероятностей его возможного выбора. Таким образом, для каждого участника возникает ситуация, аналогичная игре с природой, где в качестве природы выступает тип другого участника.
Традиционные подходы к решению подобных задач основаны на числовом представлении исходных параметров, и значения вероятностей (1) и элементы оценочной матрицы (2) задаются как точечные числа.
В ряде работ [2] отмечается, что определение значений соответствующих вероятностей и элементов матрицы (2) сопряжено с достаточно большими трудностями и следует принимать во внимание неточный характер этих оценок. В связи с этим в большом количестве известных исследований отмечается, что более реалистичными могут оказаться модели, в которых значения элементов платежной матрицы (функции потерь) задаются приближенно, для чего используются нечеткие числа [3–10]. В то же время в этих работах рассматриваются ситуации, когда априорные вероятности состояний природы остаются в форме точечных чисел, а для выбора наилучшего решения используется байесовский принцип [6–9]. Кроме того, из-за сложности используемых математических преобразований в этих работах ограничиваются использованием только нечетких чисел в LR-представлении (треугольных или трапецеидальных), что лишает общности получаемые результаты. Ранее отмечалось, что модель Дж. Харшаньи может рассматриваться как аналог игры с природой. В работе [11] рассматривается нечеткий вариант модели Дж. Хар-шаньи, в которой априорная вероятность, характеризующая тип участника (аналог природы), задается в виде нечеткого числа.
Наиболее общей постановкой рассматриваемой задачи в нечеткой форме будет представление параметров ситуации, требующей принятия решений, в виде нечетких, лингвистических утверждений.
Постановка задачи
Ситуация, требующая принятия решений, задана:
-
- множеством стратегий рационального участника ситуации, требующей принятия решений,
A= [ a i :i=1,N } ;
-
- множеством объективных условий, в которых приходится принимать решения (состояния природы)
S= { S j :j=1,M } ;
-
- множеством нечетких оценок возможности возникновения S j е S
P (S) = [ ~p (Sj ) :j=1N} ;(3)
-
- матрицей нечетких оценок последствий принятия решения a i е A при условии S j е S
G= { gij:i=1N,j=1M }.(4)
Определены терм-множества нечетких лингвистических значений для (3)
L(P)= {lk(p):k=1K }.(5)
Например: {маловероятно, достаточно вероятно, очень вероятно}. Термин «вероятно» здесь используется не в статистическом смысле. Сразу отметим, что такой набор используется только в качестве примера. Для каждой задачи он будет формироваться специально.
Аналогично должно быть построено терм-мно же ство для элементов матрицы G :
L(G )= [lq(g):q=1Q }.(6)
Элементы терм-множеств (5), (6) формализуются нечеткими множествами
M(P) = {pik (x)/ x : x е [0,1]},
M(G) = [pq(У)/ У : У е [Уmin, ymax ]},
[ y min , y max ] – область определения элементов матрицы G.
Ограничений на выбор функций принадлежности (7) и (8) не накладывается. Следует только отметить, что, выбирая тот или иной вид функций принадлежности, можно моделировать различный уровень неопределенности соответствующих оценок [12; 13].
В традиционных ситуациях, требующих принятия решений и формализуемых как игра с природой, влияние вероятностей состояний природы учитывается через вычисление средней оценки возможного решения по всему множеству состояний природы.
В случае лингвистических оценок это невозможно. Поэтому влияние неуверенности в оценке состояний природы предлагается учитывать через изменение истинности лингвистических значений последствий возможных решений.
В общем случае функция принадлежности – это непрерывная функция соответствующего аргумента. В практических расчетах используется конечное, дискретное множество значений функции принадлежности. Для учета влияния нечетких, лингвистических оценок возможности возникновения каких-то состояний природы на истинность оценок последствий принятого решения предлагается следующая процедура, которую можно рассматривать как аналог процедуры «мутация», известной в генетических алгоритмах и которая состоит в случайном изменении параметров некоторых, случайно выбранных, элементов популяции.
Решение игры с природой с нечеткими лингвистическими параметрами
Рассмотрим некоторую стратегию a i е A и состояние природы S j е S . Пусть функция принадлежности нечеткой оценки для этой комбинации задана множеством ее дискретных значений M(a i ,S j ). Для сокращения записи опустим символы a , s , оставив только индексы i и j : Y= { yt:t=1,T }
M ( i , j ) = К j ( yt ) : t е 1, T }, V i , j ( yt ) е [0, 1], yt е [ У min , У max ].
Множество Y={yt:t=1,T} будем рассматривать как некоторую популяцию, элементы которой обладают свойством v i j ( yt ). На популяцию оказывает воздействие некоторое внешнее влияние, характеризуемое набором состояний W={w j :j=1,J} с интенсивностью V ( W j ) е [0,1], возникающее случайно. Мутация популяции состоит в случайном выборе пары ( y t ,w j ), а изменение свойств элементов популяции определяется как
V ( yt ) = min [ V , j ( yt ), Ж w j ) ] . (9)
( yt , w j )
Описанное преобразование применяется ко всем элементам строк матрицы (4), в результате чего каждому из них будет соответствовать нечеткое множество с функцией принадлежности вида (9).
Если рассматривать в целом всю совокупность нечетких множеств вида (9) конкретной строки матрицы (4), то ее можно интерпретировать как нечеткое множество
MaS y ) = Ж 4 yt )}, VaS yt ) е [О,!], yt е [ y min , y max ], i = 1 M U0)
с произвольным распределением значений функций принадлежности V a ( yt ), что делает практически невозможным нахождение наилучшего решения.
В связи с этим предлагается применить к нечетким множествам (10) преобразование FztoTriangle, определенное в нечеткой таблице FuziCalc фирмы FuzzyWare, которое состоит в замене произвольного нечеткого множества эквивалентным нечетким с треугольной функцией принадлежности. При этом оба множества имеют одинаковые носитель и координату центра тяжести. Координата модального значения эквивалентного нечеткого множества yR=3*yCG SyL+yRS, (ii)
CG L R где Уа - координата центра тяжести нечеткого множества Ma. (y); ya. ,Уа соответственно, левая и правая границы носителей нечетких множеств.
Значение функции принадлежности эквивалентного нечеткого множества в точке ya,
V ( y * ) = max [ V a. (y t)] .
yt
Построенные таким образом эквивалентные нечеткие множества можно интерпретировать как нечеткую интегральную оценку последствий возможного решения на пространстве состояний природы.
Обозначим как
E (ai) = { V E(a,)( y ) >y е [ yL,yR ]},i = 1N , U2)
эквивалентное нечеткое множество, соответствующее стратегии ai. Для выбора наилучшего решения необходимо каким-то образом сравнить эти множества. В данном случае критерии сравнения должны учитывать по крайней мере два параметра сравниваемых множеств (12) – положение на области определения и уровень нечеткости. В качестве первого критерия можно использовать координату центра тяжести множества (12) либо координату его модального значения. Второй критерий – показатель размытости (нечеткости) – может определяться различными методами [14]. Показатель размытости имеет и самостоятельное значение, так как он свидетельствует о том, что выбранное в качестве наилучшего решение лишь в какой-то степени соответствует этому предположению. Одним из методов определения этого показателя нечетких множеств может быть метод, предложенный в [15], согласно которому размытость определяется как
F(x) = 2 ^ (xi)(1 - ^ (xi )
В качестве обобщенного критерия определения наиболее предпочтительного решения предлагается следующий:
•
. Y~ F“(y)’ где ya - координата центра тяжести нечеткого множества (12) либо координата его мо- дального значения.
Очевидно, что чем больше (правее на области определения) значение ya и меньше размытость Fa (у) , тем больше оснований считать альтернативу a i наиболее предпочтительной.
Для подтверждения работоспособности предлагаемых решений рассмотрим следующий пример.
Множество состояний природы S=(s1,s2,s3,s4) - нечеткие оценки, возможности возникновения которых формализованы нечеткими множествами с треугольными функциями принадлежности, представленными на рисунке, выбраны только из соображений простоты графического представления.
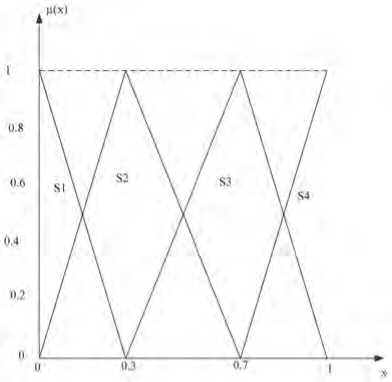
Рисунок 1. Функции принадлежности нечетких оценок возможностей состояний природы
Источник: здесь и далее рисунки выполнены автором.
Решение игры с природой с нечеткими лингвистическими параметрами
Рациональный участник располагает стратегиями A=(a1,a2,a3,a4), нечеткие лингвистические оценки последствий которых при различных состояниях природы заданы таблицей. Соответствующие функции, принадлежности приведены на Рисунке 2.
Таблица
Нечеткая платежная матрица
|
s 1 |
s 2 |
s 3 |
s 4 |
|
|
a 1 |
S |
LM |
M |
HM |
|
a 2 |
LM |
HM |
M |
B |
|
a 3 |
LM |
M |
M |
HM |
|
a 4 |
S |
HM |
HM |
LM |
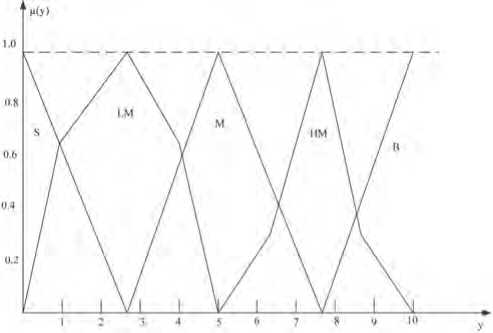
Рисунок 2. Функции принадлежности нечетких элементов платежной матрицы
Необходимо отметить, что значения, указанные в Таблице, были выбраны произвольно, как и функции принадлежности, чтобы проиллюстрировать возможности предлагаемого метода.
На Рисунках 3 и 4 представлены результаты выполнения описанных выше преобразований для двух стратегий a 2 и a 3 (см. Таблицу).
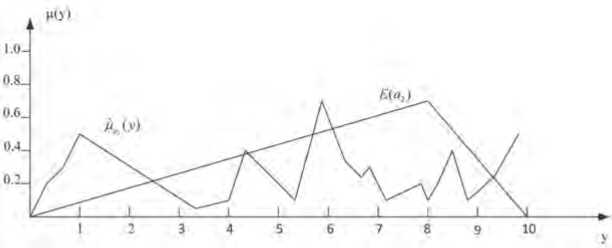
Рисунок 3. µ ˆ a (y) – результат преобразования (9) для стратегии a 2 ;
E(a2 ) – эквивалентное нечеткое множество
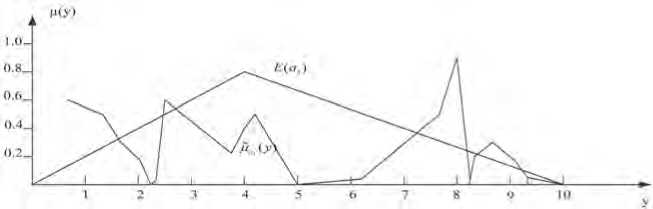
Рисунок 4. fa (y) - результат преобразования (9) для стратегии a 3 ;
E(a3 ) - эквивалентное нечеткое множество.
Расчеты по соотношению (13) дали следующие результаты: Y (a1)=0,06 ; Y (a2)=2,03 ; Y (a3)=0,67 ; y (a4)=1,38 ; соответствующее распределение предпочтительности a2 > a4 > a3 > a 1 .
Важным вопросом будет повторяемость результатов при различных реализациях алгоритма формирования нечетких множеств (10). Очевидно, что значения соответствующих координат центров тяжести и модальных значений, а также оценки (13) будут меняться, но при этом при различных реализациях должно сохраняться распределение предпочтительности.
На Рисунке 5 представлены результаты проверки повторяемости при различных реализациях предложенного метода, естественно, при одних и тех же исходных данных, то есть полученное ранее распределение предпочтительности сохраняется.
Расчеты по соотношению (13):
Y (a1)=0,208; Y (a2)=2,17; Y (a3)=0,58; Y (a4)=1,43 , a 2 > a 4 > a 3 > a 1 .
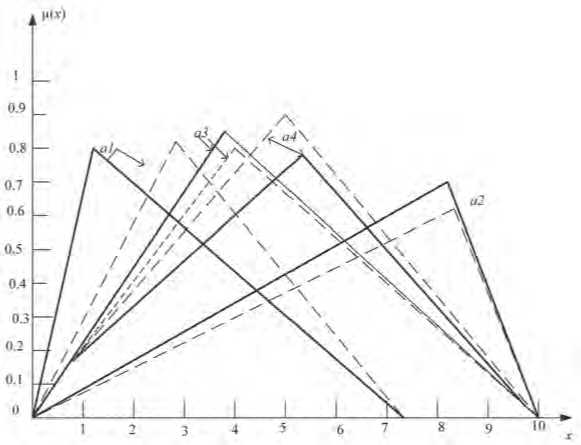
Рисунок 5. Проверка повторяемости результатов предложенного метода
Решение игры с природой с нечеткими лингвистическими параметрами
Заключение
Предложенный метод позволяет находить наиболее выгодные стратегии в ситуациях, требующих принятия решений, формализуемых как игра с природой, в условиях, когда исходные параметры имеют форму нечетких, лингвистических утверждений без ограничений на вид функций принадлежности соответствующих нечетких множеств.
Список литературы Решение игры с природой с нечеткими лингвистическими параметрами
- Харшаньи Дж., Зелтен Р. Общая теория выбора равновесия в играх / Пер. с англ. Ю.М. Донца, Н.А. Зенкевича, Л.А. Петросяна и др. СПб.: Экономическая школа, 2001.424 с. ISBN 0-262-08173-3.
- Сигал А.В. Теория игр для принятия решений в экономике: монография. Симферополь: Диайпи, 2014. 303 с. ISBN 978-966-491-551-7. EDN UJCIGT.
- Maschenko S.O. On a value of matrix game with fuzzy sets of player strategies // Fuzzy Sets and Systems. 2023. Vol. 477. No. 1. Article no. 108798. P. 2–14. DOI: https://doi.org/10.1016/j.fss.2023.108798
- Acozhen Situ Evolutionary Stable Strategies in Game with Fuzzy Payoffs // Artificial Intelligence Evolution. 2020. Vol. 1. No. 2. P. 63–71. DOI: https://doi.org/10.37256/aie.122020420
- Whalen T. Decision making under uncertainty with various assumptions about available information // IEEE Transactions on Systems, Man, and Cybernetics. 1984, Nov.-Dec. Vol. SM C-14. No. 6. Р. 888–900. DOI: 10.1109/TSM C.1984.6313316
- Шведов А.С. О допустимых и байесовских решениях при нечетких значениях функции потерь // Дискретная математика. 2021. Т. 33. № 2. С. 166–174. EDN EHM PYG. DOI: https://doi.org/10.1515/dma-2022-0013
- Viertl R. Statistical Methods for Fuzzy Data. Chichester: Wiley, 2011. 256 p. ISBN 0470699450.
- Kahraman C., Kabak Ö. Fuzzy statistical decision making // Kahraman C., Kabak Ö. (Eds) Fuzzy Statistical Decision-Making. Studies in Fuzziness and Soft Computing. Vol. 343. Springer, Cham, 2016. DOI: https://doi.org/10.1007/978-3-319-39014-7_1
- Zhen Z., Runtong Z., Yan P., Yihong R., Jie W. Fuzzy valuation-based system for Bayesian decision problems // Journal of Intelligent & Fuzzy Systems. 2016. Vol. 30. No. 4. P. 2319–2329. DOI: https://doi.org/10.3233/IFS -152002
- Wenting Xue, Zeshui Xu, Xiaomei Mi. Solving hesitant fuzzy linguistic matrix game problems for multiple attribute decision making with prospect theory // Computer & Industrial Engineering. 2021. Vol. 161. November. Article no. 107619. DOI: https://doi.org/10.1016/j.cie.2021.107619
- Чернов В.Г. Выбор решений в конфликтной ситуации с нечеткими типами участников // Искусственный интеллект и принятие решений. 2022. № 4. С. 24–36. EDN EWXKIN. DOI: 10.14357/20718594220403
- Dubois D., Prade H. Théorie des possibilités Applications à la représentation de connaissances en informatique. Paris: Masson, 1980. 292 p. ISBN 2-225-81273-X.
- Чернов В.Г. Выбор решения на основе нечеткой игры с природой // Прикладная информатика. 2021. Т. 16. № 2 (92). С. 131–143. EDN KQDDLI. DOI: 10.37791/2687-0649-2021-16-2-131-143
- Ибрагимов В.А. Элементы нечеткой математики. Баку: Изд-во АГПУ, 2010. 392 с.
- Dubois D., Prade H. New Results about Properties and Semantics of Fuzzy Set-Theoretic Operators // Wang P.P., Chang S.K. (Eds) Fuzzy Sets. Springer, Boston, MA. Pp. 59–75. DOI: https://doi.org/10.1007/978-1-4684-3848-2_6


