Решение интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом с помощью системы символьной (аналитической) математики Maple

Solving of a Fredholm’s integral differential equations with time delay using the system of symbolic (analytical) mathematics Maple

В работе [2] рассматривается начальная задача:

7=0 1=0

+л J Kti (х, nV’ («, Ш^пА = У(Х),   ^

КДх,?) =

= f ^(хл)

у⁽Ди/х)) = фДи/х_))Д = 0,п-1,х е E_v (2) где w₀(x) = x, иДх)<х, функции иДх), /) (х) и Дх) - непрерывны, ядра К., (х,^) -регулярны в квадрате а<х,г]<Ь, Е =

= lEi , Е* - множество точек, для кото- рых соответствующие иДх)йх при х>х0 y/ = U, а Е^ = [а, хо], функции фДх^ -заданы.

В этой работе с опорой на одну из модификаций функции гибкой структуры было показано, что задача (1)-(2) для уравнений запаздывающего типа (еслиД(х) = 0 и К,,Дх,7^ = 0 Ч] = Ц,а /л0(х) = 1) всегда сводится к разрешающему интегральному уравнению смешанного типа Вольтерра-Фредгольма с обыкновенным аргументом

I ¹¹ Ло /^р£ J еДх.^р^¹*

7-0

-t)

J Д(хд)^(г)(/Г = Дх), где ядра Q^x,0, Nj(x,t) и функция S(x)

находятся по следующим формулам:

+К^х,0, j^0 j=0t=|

+л I к„ (х,?)-----—^1+

с

‘7

Задачу (1Д2) преобразуем к разрешающему уравнению (3), используя математический пакет Maple, который имеет собственный язык программирования, позволяющий создавать пользовательские программы, и отличается от других языков программирования тем, что в нем уже реализованы многие алгоритмы. Например, команды diff(F,x), int(F,x), которые дифференцируют и интегрируют функцию F по переменной х.

В Maple имеется довольно широкий набор команд и конструкций, аналогичный существующим в известных языках программирования (например, в языках Pascal или С): операторы присваивания, ветвления, цикла for, while, операторы прерывания и обработки ошибок. Также преду-

Г.А. Шишкин, ОД. Ринчинова. Решение интегро-дифференциальных уравнений Фредгольма с запаздывающим аргументом с помощью системы символьной (аналитической) математики Maple                    14$ смотрены способы объявления процедур и модулей.

Для        решения        интегро- дифференциального уравнения Фредгольма создадим модуль, из которого будут экспортироваться ядра 5y(x,f), N^хД и функция В^, с опцией «пакет». Локальные процедуры: MatrD, MatrDelta, С, вы-

• >    tdyf:=module()

export QNucleus,NNucleus,BNucleus;

option package;

local MatrD,MatrDelta,c;

MatrD:=proc(R,n)

end proc:

MatrDelta: = proc(MD,R,S Str, Variables)

end proc:

c:= proc(u,xO,b)

считывают, соответственно, матрицы D, As и корни с , которые определяются из уравнения и^х^-х^ на отрезке [х₀, />], если же таковых нет, то выбираются соответствующие Cj = b.

Процедуры, используемые в модуле:

end proc:

QNucleus: = proc(R,U,F,n,l)

local Q,i,j;

Q:=array(l..l+1);

for j from 1 to 1+1 do for i from I to n+1 do ifi> 1 then

Q[j]: = Q[jl + F[i,j]*diff(det(MatrDe!ta(MatrD(R,n),R,n,U[j]-t,n)),x$(i-l)); else

Q[j]:=F[i,j]*det(MatrDelta(MatrD(R,n),R,n,U[j]-t,n)); fi; od;

Q[j]:=det(MatrD(R,n)A(-l))*Q[j];

od;

eval(Q);

end proc:

NNucleus: = proc(R,U,K,nJ)

end proc:

BNucleus:= proc(R,U,K,F,f,xO,b, lambda, Phi, nJ)

end proc:

save idyfj’idyf.m"; end module;

Программа позволяет пользователю получить из начальной задачи (1)-(2) разрешающее интегральное уравнение смешанного типа Вольтерра-Фредгольма с обыкновенным аргументом (3).

уДх) + хуДх - 1)-2 ^цуСДВц = хе^х~\ о

- у(х) = х,у'(х) = 1 на Eq = [0], /(х-1)=х-1,У(х-1) = 1 на Е'_й =[-1,0].

Для получения доступа к процедурам пакета его необходимо подключить командой (with(idyf);). Зададим исходные данные:

Рассмотрим задачу Коши при начальном значении т, =0 для уравнения запаздывающего типа:

• >    п:=2:

• 1:    = 1:

а:=0:

b:=i:

F: = matrix([[0,0],[0,x],[l,0]]):

K:=matrix([[eta*exp(x),0],[0,0],[0,0J]):

U:=vector([x,x-I ]):

Phi: = matrix([[x,l ],[x-l, 1 ]]):

R: = vector([0,l J):

x0."0:

f:=x*exp(x-1):

lambda:=2:

R - определитель Вандермонда, составленный     из неопределенных параметров       rpj = 1,н, которые определяются в ходе решения задачи, исходя из оптимальности ее решения. В данном примере взято (0, 1).

Обратимся к процедурам QNucleus, NNucleus, BNucleus

QNucleus(R,U,F,n,i);

NNuckus(R,U,K,nJ);

BNucleus(R,U, K, F,f,xO,b, lambda, Phi, nJ);

Первая процедура вычислила ядра ^y(xJ) и результаты выводятся на рабочий лист

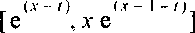
Соответственно, ядра No и М

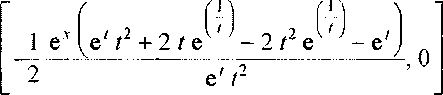
и функция 5(х)

-2 еЛ -

Таким образом, мы имеем разрешающее интегральное уравнение смешанного типа Вольтерра-Фредгольма с обыкновенным аргументом вида (3).