Решение электротехнических задач методом преобразования Лапласа при помощи математического пакета MathCAD

Рассмотрим одиночный замкнутый электрический контур со следующими параметрами (Рис.1.)

R

e(t) i(t) C

L

I___mm_______

Рис. 1. Электрический контур

В этом контуре находится генератор, создающий переменное во времени напряжение e(t) , которое вызывает в контуре ток i(t). Падение напряжения равно L^ на индуктивности, Ri — на сопротивлении и ¹ ^ i(t)dt — на емкости. Согласно закону Кирхгофа, суммарное падение с ^-^ напряжения в контуре равно приложенной электродвижущей силе e(t), следовательно, имеет место уравнение (1).

t

di

Ldt + Ri + c

J i(r)dT = e(t)

-та

Это интегро-дифференциальное уравнение, определяющее ток i(t), можно преобразовать в дифференциальное уравнение второго порядка (2)

если в качестве новой переменной ввести заряд конденсатора k⁽t) = il_mi⁽T№.

d2k    dk 1

-      ■       '              ■                   (2)

В дальнейшем в целях лучшей обозримости вычислений примем, что контур в момент времени t = 0 находился в состоянии покоя.

Тогда для уравнения (1) соответствующим ему изображающим уравнением будет:

LpI(p) + RI(p) + -^I(p) = E(p) Lp

Введя для

сокращения записи обозначение Lp + R + -1 = Z(p), получим уравнение (3).

Z(p)I(p) = E(p)     (3)

Функцию I(p) назовем током , а функцию E(p) — напряжением .

Тогда на языке пространства изображений уравнение (3) будет выражать не что иное, как закон Ома, если только функцию Z(p) назвать сопротивлением. Однако вместо этого названия для функции Z(p) принят термин импеданс.

Для примера решим следующую задачу. Дана схема (Рис.2) со следующими исходными данными: E = 100 В, R 1 = 20 Ом, R 2 = 5 Ом, L = 100мГн, L = 10мкФ. Пусть в момент коммутации емкость была

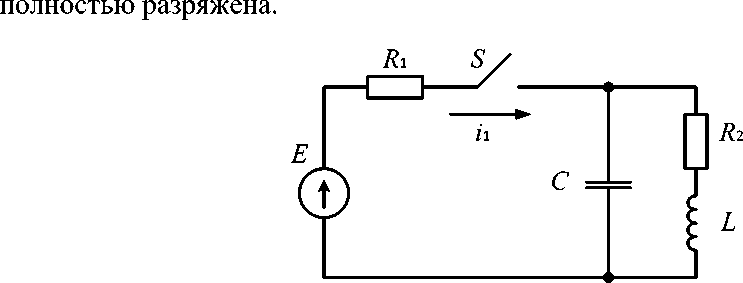
Рис. 2. Исходная схема электрической цепи

Необходимо определить значение входного тока после замыкания ключа.

Изобразим операторную схему замещения (Рис.3)

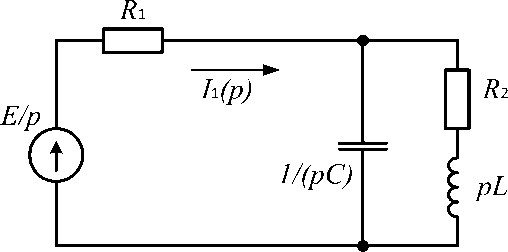
Рис. 3. Операторная схема замещения

Общее операторное сопротивление цепи равно:

(Кг + рС)-1

2(р) = Ri +--------РГ

й2 + РС+рс

Преобразовав это выражение и, для упрощения расчетов, введя новые переменные, получим:

Ьгр2 + bip + Ьо

Р    а2р2 + а1р + 1,

где Ь2 = К^Г, Ь1 = К1К2Г + L, b0 = R1 + R2 ,а2 = СГ, а1 = К2Г

Изображение тока 1 1 (р) по закону Ома будет

;    _ Е _ Е(а2р2 + а1р + 1)

1р pZ(p) р(Ь2р2 + Ь1р + Ьо)

Приравняв нулю знаменатель этого выражения, мы, как и следовало ожидать, получим нулевой корень, соответствующий действию в цепи источника постоянной ЭДС, и еще два корня

• -Ь1 ±1Ь12-4Ь2Ьо

• ^р 1'2 = -------- 2Ь 2---------

  при исходных данных задачи равные р 1 = -261 и р₂ = -4789

Для определения оригинала тока воспользуемся выражением

_ F1(Р) _ F1(Р) , V  Fi(Pk) Ptt _

• (Р)  F2 (р)  F3(p) + LlpkF'2(Pk)      Ю

к=0

Тогда ток 1 1 (f) будет равен

() = Е_  Е(а2р12+а1р1 + 1)  1t Е^2 + Я1Р2 + 1)

• 1      bo      Р1(2Ь2Р1 + Ь1)              Р2(2Ь2Р2 + Ь1)

Подставив числовые значения, окончательно получаем:

i1(t) = 4 - 4,46e-261t + 5,46e-4789t (А)

Построим график в программе MathCAD (Рис.4).

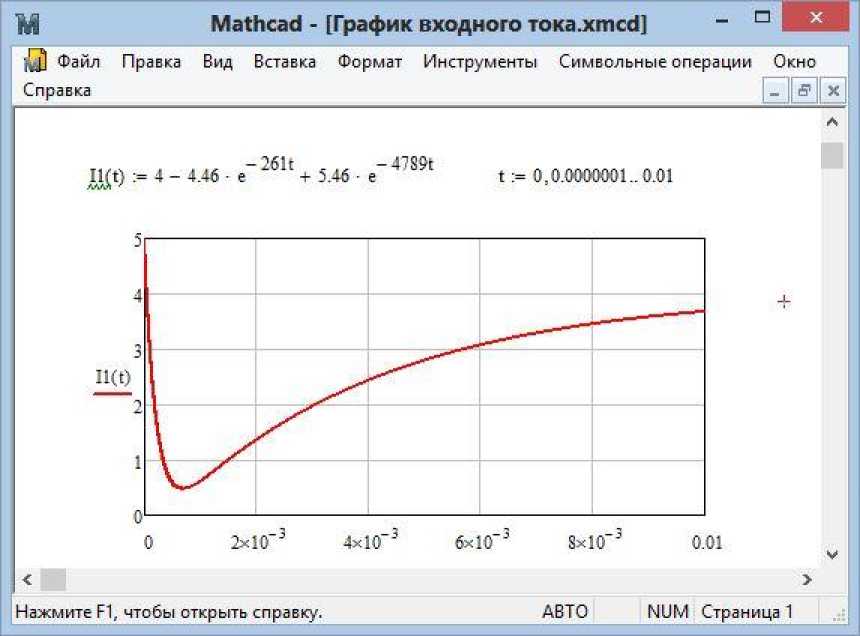
Рис. 4. График входного тока в MathCAD

При помощи встроенной функции обратного преобразования Лапласа в математическом пакете MathCAD, можно решить данную задачу гораздо быстрее. Пример такого расчета приведем ниже (Рис.5).

Сравнивая уравнения для тока, рассчитанного "вручную" и при помощи программы MathCAD, можно сказать, что они идентичны, т.к. если представить гиперболический синус и гиперболический косинус в виде экспонент, то мы придем к такому же уравнению, что получили ранее.

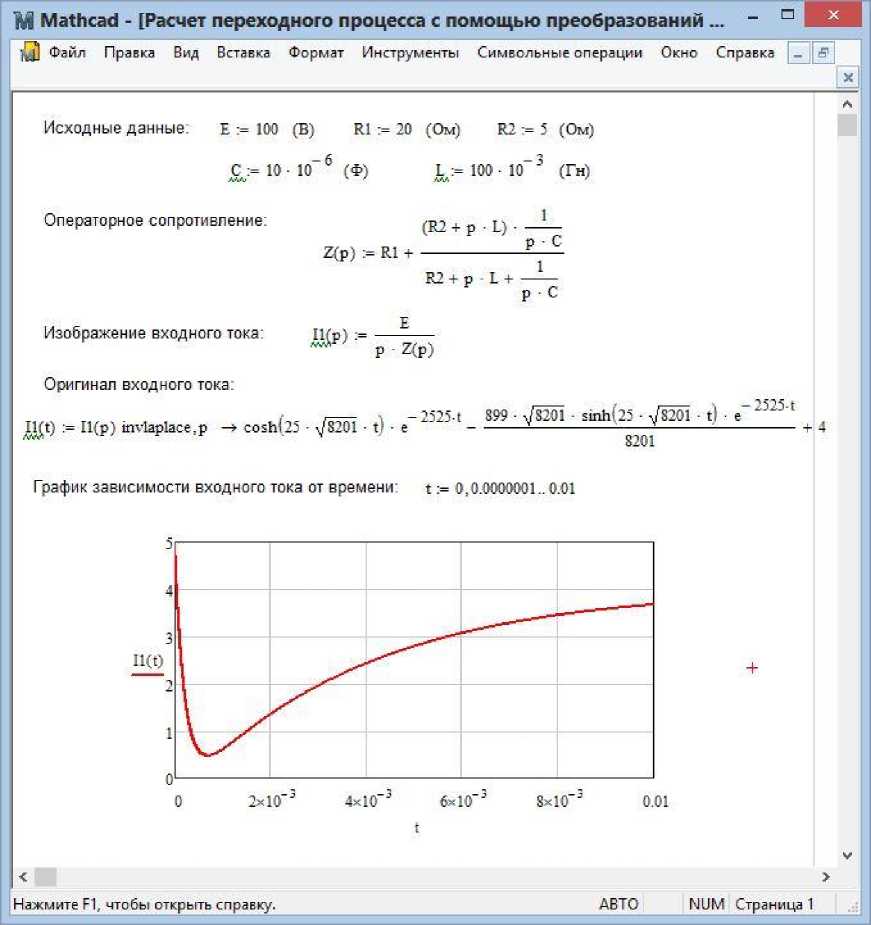
Рис. 5. Пример расчета в программе MathCAD

Таким образом, использование обратного преобразования в математическом пакете MathCAD намного упрощает задачу нахождения параметров электрической цепи.