Решение линейной обратной задачи с использованием компьютерной технологии "GRANM"

Важнейшей проблемой в геофизике, в частности в гравиметрии, является решение обратной задачи: по наблюденному гравитационному полю на поверхности Земли найти распределение масс в толще Земли, ответственное за наблюденное поле. Существуют два подхода к решению обратной задачи. Первый – это метод подбора.

Метод подбора заключается в многократном решении прямой задачи для некоторого пробного множества распределений масс, пока не найдется элемент множества, расчетное поле которого будет наиболее близко по какому-либо критерию к наблюденному полю. Метод подбора довольно трудоемкий, поскольку требует решения большого объема прямых задач.

Второй поход заключается в прямом (аналитическом) продолжении заданных на поверхности Земли значений поля в нижнее полупространство и основывается на том, что в результате аналитического продолжения однозначно устанавливаются некоторые неправильности расчетного поля. В этих неправильностях (особых точках) значения гравитационного поля ме-

няются скачкообразно или обращаются в бесконечность. Найденные особые точки одновременно представляют геометрические особенности контуров поперечных сечений поверхностей возмущающих тел, которые могут быть выражены в виде резких изломов, разрывов и других искажений. Таким образом, по поведению расчетного аномального поля, полученного в результате аналитического продолжения измеренных значений поля на поверхности Земли, косвенно определяется и поверхность возмущающего тела. Что касается избыточной плотности тела, то она устанавливается по гравитационной аномалии.

В ранних работах в рамках второго подхода (Андреев, Клушин, 1965) задача аналитического продолжения решалась с использованием сеточного метода и некоторых математических теорем. Например, в двумерном случае использовалась теорема о том, что значение гармонической функции в центре окружности равно среднему арифметическому значений функции на самой окружности. Тогда, с использованием этой теоремы, по измеренным на поверхности Земли (z=0) и на уровне (профиле) выше поверхности на шаг сетки (z=h) значениям гравитационного поля можно найти значения поля на уровне (профиле), расположенном на глубине в один шаг сетки в нижнем полупространстве. Найденные значения используются для вычисления поля на уровне, находящемся на глубине уже в два шага сетки в нижнем полупространстве и т.д. Этот последовательный пересчет сверху вниз от уровня к уровню и от узла сетки к узлу на данном уровне приводил к быстрому накоплению погрешностей, неизбежно сопровождающих процесс вычислений (это погрешности, связанные с ошибками измерений, погрешности при округлении и т.п.). Как отмечают сами авторы (Андреев, Клушин, 1965), поле удавалось продолжить в нижнее полупространство всего на 1-3 шага сетки.

Эта ситуация начала меняться в результате появления в начале этого века высокопроизводительной вычислительной техники. Теперь задачу аналитического продолжения наблюденных значений поля в нижнее полупространство можно свести к задаче составления и решения систем линейных алгебраических уравнений больших порядков. Использование современных вычислительных систем позволяет решать такие системы за приемлемое время. Редуцирование задачи аналитического продолжения к задаче составления СЛАУ осуществляется путем замены непрерывного пространства сеточным пространством и применения дискретного уравнения Лапласа (Самарский, 1971). Поскольку в этом случае значения поля вычисляются сразу во всех узлах заданного сеточного слоя в нижнем полупространстве и нет последовательного пересчета, то погрешности, о которых речь шла выше, перераспределяются в процессе решения СЛАУ между всеми значениями поля и тем самым нивелируются.

Вместе с тем при реализации второго подхода к решению обратной задачи, основанного на аналитическом продолжении заданных на поверхности Земли значений гравитационного поля с использованием уравнения Лапласа, возникают определенные трудности математического характера. Первая проблема возникает при постановке задачи аналитического продолжения наблюденных значений поля в заданный сеточный слой в нижнем полупространстве. С математической точки зрения решение задачи аналитического продолжения означает решение задачи Дирихле для уравнения Лапласа в прямоугольнике в предположении, что известны краевые условия по контуру прямоугольника (в условиях двумерной задачи). В гравиметрии заданные, т.е. наблюденные на поверхности Земли, значения поля расположены только на части контура прямоугольника (заданного сеточного слоя) – стороне прямоугольника, противоположной его основанию. Очень редко заданные значения поля известны по боковым сторонам прямоугольника (только в случае, если гравиметрическая съемка проводилась в шурфах или подземных выработках). Что касается значений поля, расположенных на основании прямоугольника, то их как раз и необходимо найти в результате аналитического продолжения вниз.

Таким образом, задача аналитического продолжения наблюденных на поверхности Земли значений гравитационного поля в нижний заданный сеточный слой является некорректно поставленной. Некорректность постановки задачи приводит к неустойчивому решению СЛАУ, возникающей в результате редуцирования непрерывной задачи аналитического продолжения к задаче составления и решения систем линейных алгебраических уравнений. Некорректно поставленная задача решалась путем «принудительной» регуляризации, состоящей в присоединении дополнительных уравнений к прежней СЛАУ. Для этого рассматривались совместно две и более дискретные аппроксимации дифференциального оператора Лапласа и полученные таким образом переопределенные СЛАУ решались уже устойчиво (Страхов и др., 2001).

Следующая проблема состояла в необходимости разработать метод устойчивого решения систем линейных алгебраических уравнений больших порядков. Такой метод был предложен академиком В.Н. Страховым (Страхов В.Н., Страхов А.В., 1999) и основывался на классическом подходе к использованию полиномов от матриц вместе с идеей подавления компонент спектра полезного сигнала.

Далее было необходимо разработать методику оценки точности расчетных значений поля в модельных примерах, полученных в результате решения СЛАУ в нижнем полупространстве, чтобы оценить степень близости интерпретационной картины, полученной в результате аналитического продолжения, к истинной. Если рассматривать тела простейших геометрических форм в качестве возмущающих объектов, то соответствующие интегралы, описывающие поля гравитационного потенциала и его производных (решения так называемой прямой задачи), вычисляются в конечном виде. Особенно простой вид решения прямой задачи имеют в двумерных условиях, которые здесь и рассматриваются. Следовательно, если в результате решения прямой задачи иметь в распоряжении аналитические формулы для гравитационных полей возмущающих тел простейших форм и принимать их значения в задаче аналитического продолжения в качестве заданных (измеренных) значений поля на поверхности Земли, а полученные в результате решения СЛАУ значения поля в нижнем полупространстве сравнивать по какой-либо норме с точными решениями той же прямой задачи в соответствующих точках, то можно оценивать точность значений поля, полученных в нижнем полупространстве при аналитическом продолжении.

Помимо решения задач постановочного характера и оценки точности расчетных значений поля решались следующие проблемы: фильтрация (обработки) вектора заданных значений поля, осложненного высокочастотной помехой; разработка технологий, позволяющих повысить точность расчетных значений поля в нижнем полупространстве; приведение результатов гравиметрической съемки к виду, необходимому в технологии оконтуривания при решении практических задач, и др.

Для решения вышеуказанных задач были разработаны соответствующие компьютерные программы, объединенные затем в пакет программ «GrAnM» . В состав пакета также входит специальная компьютерная программа, визуализирующая результаты расчетов.

С использованием пакета программ «GrAnM» были проведены многочисленные вычислительные эксперименты в модельных условиях для установления закономерностей в поведении расчетного поля в нижнем полупространстве при аналитическом продолжении заданных значений гравитационного поля на уровнях z=0, z=-h (h – шаг сетки; ось Oz направлена вниз) в нижнее полупространство с помощью дискретного уравнения Лапласа ( Арсану-каев , 2003, 2004, 2009, 2010, 2013, 20142017). В качестве аномалиеобразующих объектов принимались, как уже отмечалось, однородные тела простейших геометрических форм и их комбинации. Например, рассматривались модельные примеры для разрезов (все бесконечной протяженности в направлении оси Oy), состоящих: а) из трех прямоугольных параллелепипедов – вертикальных пластов (геологический аналог – блоковые структуры типа горстов или грабенов) с различными избыточными плотностями; б) куполовидной структуры, также сложенной из вертикальных пластов (геологический аналог – соляные купола или карстовые пустоты); в) кругового горизонтального материального цилиндра (геологический аналог синклинальных или антиклинальных складок) и др. Параметры математических моделей этих разрезов (а именно шаг сетки, длина профилей, на которых расположены значения гравитационного поля, расстояние до верхней кромки возмущающих тел, геометрические размеры тел, избыточные плотности) принимались примерно одинаковыми.

«Измеренные» значения аномального гравитационного поля для этих разрезов находились в результате решения прямой задачи для вертикального пласта (в случае куполовидной структуры принималась суперпозиция решений прямых задач для пластов, слагающих структуру) и кругового горизонтального материального ци- линдра, представленных в виде соответствующих интегралов, каждый из которых вычисляется в квадратурах и, таким образом, дает точное решение прямой задачи соответственно (1), (2) (Андреев, Клушин, 1965):

Ag = fa x In (x2 + z2)+ 2arctgx z x2z2

, (1)

x ₁ z ₁

~ h

Ag = 2 fX^-y (2). x2 + h

Как уже отмечалось, точные решения прямой задачи (1), (2) используются не только в качестве заданных значений поля на уровнях z=0, z=-h при решении задачи аналитического продолжения, но и для оценки точности расчетных значений поля в нижнем полупространстве, получае- мых в результате аналитического продолжения. Следует отметить, что пакет программ «GrAnM» обладает «открытой архитектурой», т.е. позволяет менять модули с решением прямых задач и моделировать таким образом различные геоплот-ностные неоднородности.

Прежде чем продолжить, дадим сведения о порядке СЛАУ, возникавших здесь при рассмотрении дискретного уравнения Лапласа совместно на двух шаблонах «прямой крест» и «косой крест» (две дискретные аппроксимации дифференциального оператора Лапласа).

Порядок матриц (А) и векторов правой части (f) при аналитическом продолжении до соответствующих отметок в нижнем полупространстве для модельного примера возмущающих тел (шаг сетки 0.2 км, длина профилей, на которых расположены значения гравитационного поля, равна 32 км, расстояние до верхней кромки возмущающих тел равно 4 км, геометрические размеры тел в виде прямоугольного сечения 4.8 км x 4.4 км, избыточная плотность равна 0.1г/см3) следующий:

4км: A=6360x3220; f=6360x1,

4км: A=6996x3542; f=6996x1,

5 км: А=7950x4025; f =7950x1,

6км: А=9540x4830; f =9540x1, где

4 км – отметка верхней кромки возмущающих тел; 4.4 км – отметка на 2 шага сетки ниже отметки верхней кромки; 5 км – отметка вблизи центра тяжести возмущающих объектов; 6км – отметка вблизи центра тяжести возмущающих объектов.

В результате проведенных исследований было установлено, что элементы залегания (отметки верхней кромки и центра тяжести тел) для всех возмущающих тел определяются с хорошей точностью, а закономерности в поведении расчетного поля одни и те же. Что касается определения нижней кромки возмущающих тел, то в простейших случаях она определяется однозначно по отметкам верхней кромки и центра тяжести тел; в более общем случае для нахождения нижней кромки тел требуется априорная информация. Различия в поведении расчетного поля в нижнем полупространстве проявляются при построении функции Березкина, включающей вторые производные от расчетного гравитационного поля. Эти различия в поведении обусловлены различием форм поверхности возмущающих тел. В результате исследований по поведению расчетного поля было также установлено положение верхних особенностей по оси x отдельных элементов сложно построенного разреза ( Арсанукаев, 2017 ).

Выявленные выше закономерности в вычислительных экспериментах при аналитическом продолжении заданных значений гравитационного поля в нижнее полупространство были положены в основу компьютерной технологии оконтуривания перспективных разрезов, имеющей одноименное название с пакетом программ «GrAnM» ( Арсанукаев, 2010; Арсанукаев, Рудаковская , 2013 ). С помощью этой технологии создается библиотека решений для различных разрезов с построением атласа аномальных кривых.

Рассмотрим теперь, как в двумерном случае с использованием технологии «GrAnM» решается линейная обратная задача в модельных условиях для двух слоистых структур 1, 2 ( рис. 1, 2).

Как можно видеть из рис. 3, поведение расчетных полей в нижнем полупространстве примерно одинаково для обеих структур, отметки верхней кромки и отметки центра тяжести структур. Различие в поведении полей заметно только для функции Березкина (рис. 3, г). Таким образом, по технологии оконтуривания «GrAnM» c хорошей точностью устанавливаются положения верхней кромки и центра тяжести обеих структур. Определение нижней кромки для структуры 1 затруднительно без наличия априорной информации. Положение нижней кромки структуры 2 уверенно устанавливается по результатам определения положения нижних кромок каждого из 5 слоев в отдельности, составляющих структуру, при аналитическом продолжении с использованием технологии оконтуривания. Следует также отметить, что определение контура структуры 1 с хорошим приближением всё же не устраняет неоднозначности в определении избыточных плотностей слоев, слагающих её. Действительно, в работе (Арсанукаев, Рудаковская, 2013) рассматривалось решение прямой задачи для слоистой структуры 1 (рис. 1) с использованием всех вариантов чередования 5 слоев с 8 наборами заданных плотностей, т.е. 85 вариантов. Расчеты показали, что даже при очень низком уровне погрешности между «наблюденными» значениями и решениями прямой задачи для данного плотностного состава разреза, в качестве значимых решений следует рассматривать 17 интерпретационных моделей разреза, из которых один наиболее близок к искомому. Как было отмечено в работе, неоднозначное решение обратной задачи в случае слоистой структуры 1 в значительной степени объясняется тем, что гравитационный эффект от погребенного нижнего слоя перекрывается гравитационным эффектом от вышележащего слоя.

Таким образом, слоистая структура 1 оказалась малопригодной при решении линейной обратной задачи, и значения избыточных плотностей определялись по «наблюденным» значениям гравитационного поля для слоистой структуры 2, контур которой уже найден с использованием технологии «GrAnM» .

32 X, км

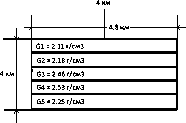
Рис. 1. Слоистая структура 1

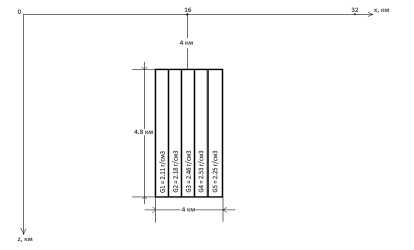
Рис. 2. Слоистая структура 2

Значения избыточных плотностей находятся в результате решения переопределенной системы линейных алгебраических уравнений, имеющей порядок 161x5:

ff i L₁ ( X₁,z₀₎ + ... + a₅L₅ ( X₁,z_O ) =q ( X₁,z_O )

O i L iq X^Z o) + ... + a₅L₅ ( X₂,Z o) = q ( X 2 ,Z o)

………………………………….... (3) ^ol^Ll(^X161^,zo) ⁺ •••^+o 5 ^L 5 ⁽-⁾ = q (^x161^,zo) , где o₁ ..o - — искомые значения избыточных плотностей ;

L i⁽ X i ,Z o⁾ ,L 2⁽ X i ,Z o⁾ .^L₅(X i6i ,z₀) - значения гравитационного поля, создаваемого каждым из 5 вертикальных пластов с единичной избыточной плотностью , составляющих слоистую структуру 2 в точках наблюдения ( X [ ,z₀) (i=1...161), расположенных на уровне z=0;

q(x₁,z₀) ... q(x₁₆₁,z₀) - заданные ( «измеренные») значения гравитационного поля, создаваемого слоистой структурой 2 в точках наблюдения ( X [ ,z₀) (i=1.161) структур на отметках 2 км, 4 км, 6 км (рис. 3, а, б, в), т.е. соответственно для отметки, равной половине расстояния между уровнем z=0 и верхней кромкой.

Подставляя в систему (3) значения L i⁽ X i ,Zo' ⁾ ,L 2⁽ X i ,Zo' ⁾ ..L₅(X i6i ,Z o ) , вычисленные по формуле (1) и значения q(x₁,z₀) .q(x₁₆₁,z₀), полученные в результате суперпозиции решений по формуле (1) для пяти вертикальных

Слоистая структура 1

Слоистая структура 2

а

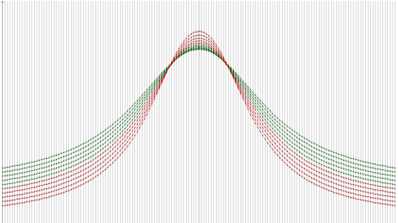
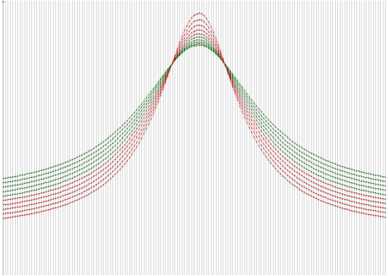
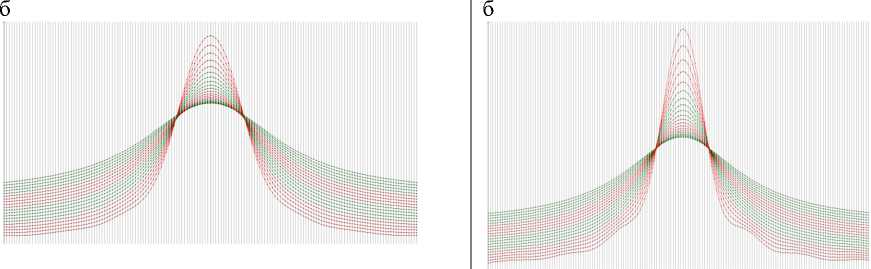
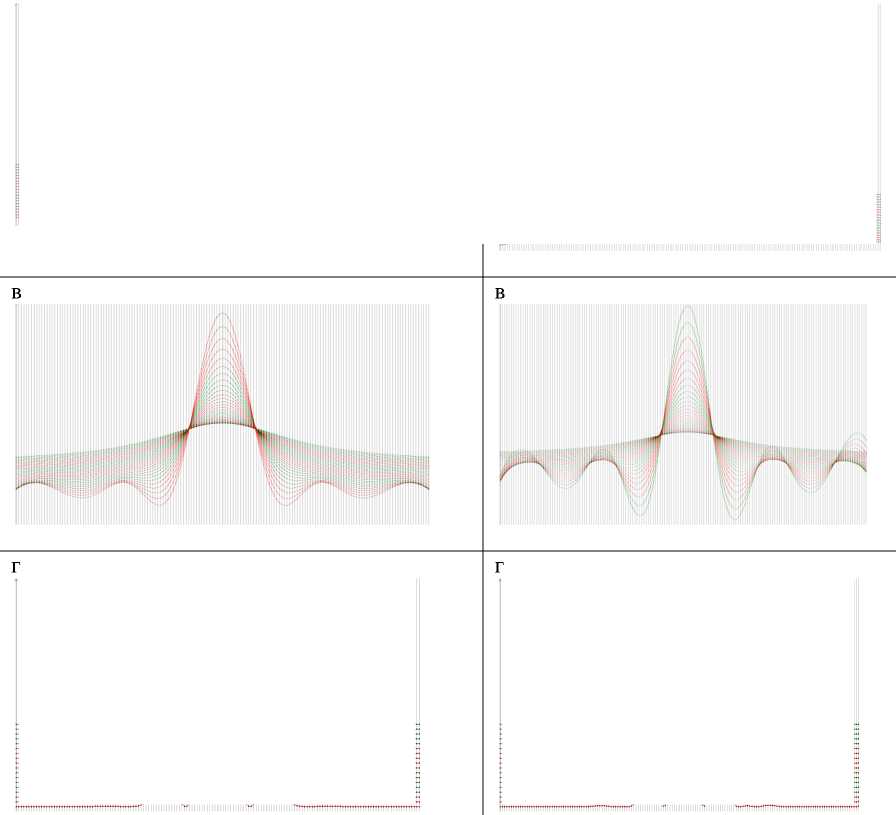
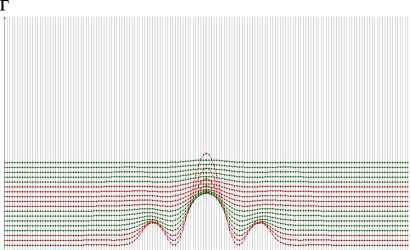
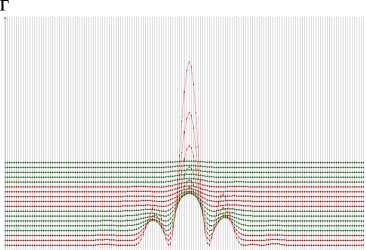
Рис 3 . Аномальные кривые и графики функции Березкина расчетных значений гравитационного поля (в 161 точках на каждом уровне) для модельного примера двух слоистых структур на профиле длиной 32 км при шаге сети, равном 200 м, при аналитическом продолжении в нижнее полупространство до отметки, равной: а – 2 км (10 кривых); б – 4км (20кривых); в – 6км (30 кривых);г– функция Березкина на отметке 4км пластов с известными плотностями (рис. 2) , составляющих слоистую структуру 2, получим систему (3’):

a ₁ 0.0131 +   + a ₅ 0.0093 = 0.0163

^0.0134 + ... + a ₅ 0.0095 = 0.0167 (3 ’ )

^0.0143 + . + a ₅ 0.0101 = 0.0178

Для решения системы (3^’) использовался метод Хаусхолдера, представляющий собой разновидность прямых методов решения СЛАУ ( Уилкинсон, Райнш, 1976 ). Были получены следующие значения избыточных плотностей (избыточные плотности находятся вычитанием из абсолютных плотностей пластов абсолютной плотности вмещающей среды, равной 2 г/см³ ):

a1 = 0.109926977696360, a2 = 0.180380071080015, a3 = 0.459271991074711, a4 = 0.530610244560195, a15 = 0.249810664371966.

Как можно видеть, расчетные значения избыточных плотностей очень близки искомым значениям.