Решение многоэкстремальных задач методом делящихся роев

Среди эвристических алгоритмов был выбран метод, наиболее подходящий для решения координатных экстремальных задач, а именно, канонический метод роящихся частиц (КМРЧ). Исследователи, основываясь на законах механики движения, предложили его модификацию для приближения предлагаемой математической модели к описанию поведения роя в природе (учитывая биологические и социальные признаки) и алгоритм, позволяющий исследовать многоэкстремальные поверхности [1].

Метод делящихся роев (МДР). В КМРЧ частица в каждый момент времени, т.е. на всех итерациях расчета t , характеризуется вектором координат x_it , определяющими ее положение, векторами скорости V i t и ускорения [2]. Далее в каждой точке x i t вычисляется значение целевой функции (критерия оптимизации) Q i t ( x i t ) (где i - номер частицы). Исходя из полученного значения Q по заданным правилам, частица меняет направление и значение ускорения, что влечет изменение скорости и положения. Закон изменения скорости частицы выражается в виде уравнения:

• V i, + 1 =« V i,t + U [0, P l ® ( x ^t — хщ ) , (1) где х^ь - вектор координат частицы с наилучшими значениями целевой функции Q ( о ) , заданной

в виде функциональной зависимости f ({ x i }) ; U [0,в] - вектор псевдослучайных чисел, равномерно распределенных в интервале [0, в]; а - свободный параметр, определяющий инерционное свойство частицы; V i, _t - скорость i -й частицы в t- й момент условного времени.

Закон изменения положения частицы выражается в виде уравнения:

• ^x i , t + 1 = ^x i , t ⁺ V i, t + 1 . ⁽²⁾

С целью применения КМРЧ к многоэкстремальным функциям выполняется его модификация в МДР. Первая модификация связана с введением понятия «антисоциальной» частицы. Такие частицы двигаются в противоположную сторону от центра притяжения, что позволяет обнаружить другие локальные и глобальные экстремумы, иными словами, это частица глобального поис- ка, повышающая эффективность обнаружения экстремумов и снижающая риск зацикливания на локальном экстремуме.

Вторая модификация связана с организацией параллельного роения нескольких роев. При обнаружении «антисоциальной» частицей области предположительного экстремума она становится центром нового роя, т.е. запускается параллельный процесс роения. Обычно новый рой имеет такие же характеристики, как и предыдущий.

В МДР рой характеризуется двумя радиусами: исходный построенного роя R^b и минимальный, т.е. создается не центр, а область притяжения роя на некотором расстоянии R^е от точки с координатами частицы.

Введенные модификации нашли отображение в математической модели КМРЧ. Уравнение закона изменения положения частицы (2):

xk , = xki f + Vk At; к = 1, Kf ,(3),

• i,    J, t+1 i, J, t i, J, t+1       ;                  ’ t ,

где K t – количество роев, образовавшихся к t - у этапу; Δ t – темп поиска, введенный в рассмотрение для облегчения настройки процесса поиска; k – номер роя.

Уравнение изменения скорости (1) принимает вид

Vk , = V, , + Ak t1 ; k = 1,Kf ,(4),

• i,    J,t + 1           i,J,t           i, J,t        ;               t ,

где А – общее ускорение частицы, которое определяется действием различных сил (сила притяжения и торможения):

\J,t = ^АР^J-t + МАtri,J,t , где ц - коэффициент «социальности» поведения частицы, р = +1 - для «социальных» частиц, т.е. частиц локального поиска, и ц = -1 - для «антисоциальных» частиц, т.е. частиц глобального поиска; p – коэффициент силы притяжения; tr – коэффициент силы торможения.

В формуле (5) каждая составляющая ускорения рассчитывается с учетом флуктуирующего параметра на основе случайной функции с симметричным распределением относительно номинала его настройки r (X, c) = X[1 + 2е( rnd(1) - 0,5)],                              (6)

где X - номинальное значение флуктуирующего параметра; е - отклонение от номинального значения.

Таким образом, результирующее уравнение закона изменения скорости для частицы локального поиска (ЧЛП) и частицы глобального поиска (ЧГП) имеет вид

• V J +, = V J ±[ ( x kГ - R kl, ) r c (^X c . е С ) - x k „] r p (^X p . е p ) ± Ot(^X t - е t ) ,   (7)

где r c ( X _c e c _c ) — обеспечивает неоднозначность положения центра притяжения; г_р(к_р,г_р) - обеспечивает неоднозначность величины ускорения; r_t(k_t,г , ) - обеспечивает неоднозначность величины коэффициента трения; х,’ _t ^extr - J -я координата наилучшего по критерию Q положения точек к -го роя за всю историю его движения от 0 до t ; R^k,j_t - проекция отрезка вектора x,^ - x i^t длиной R^e | на J -ю ось параметрического пространства поиска.

В результате роения исходного роя по законам изменения (3) и (7) ЧЛП будет найден один из экстремумов. В процессе роения заданный процент ЧЛП-частиц на определенное время становятся ЧГП, что позволяет осуществить поиск областей предположительного нахождения других экстремумов и построить новые рои, которые начнут свое параллельное роение независимо от стартового. В результате параллельно с исходным может роиться любое количество роев, каждый из которых может либо найти новый экстремум, либо сместиться в зону роения другого. Это приводит к объединению обоих роев в один.

Таким образом, МДР позволяет выполнить эффективный поиск множества экстремумов сложных функций. Результативность МДР иллюстрируется примерами его применения для нахождения экстремумов тестовых функций.

Примеры применения МДР для поиска экстремумов сложных функций. Особенность всех эвристических алгоритмов заключается в невозможности использования математического исследования их свойств и выработки эффективных настроек. В связи с этим исследование таких алгоритмов осуществляется методами имитационного моделирования на статистически значимых выборках вариантов объектов оптимизации. Таким образом, исследование МДР происходит в процессе его применения для решения задачи поиска экстремумов усложненной одномерной функции Нейдорфа и двумерной функции Химмельблау на заданном диапазоне.

При исследовании функций для одного опыта строится 50 случайно сформированных роев с заданным начальным радиусом R_b и различными центрами. Процесс роения для каждого роя происходит за заданное число итераций N all , N all = 200 .

Метод роящихся частиц с механизмом деления роя, как и большинство эвристических алгоритмов, основывается на множестве параметров настройки, т.е. результативность метода зависит от выбранных значений этих параметров. При этом значения некоторых из этих параметров зафиксированы с расчетом на правильность выбранных значений, с учетом оценок, полученных из предыдущих опытов МРЧ. К таким параметрам относятся: деморазмер роя ( m ) , исходный радиус роя ( R b ), флуктуирующие составляющие ускорения ( X p , е p ), флуктуирующие составляющие трения ( X t , е t ), флуктуирующие составляющие центра роя ( X с , е с ). Кроме этого интуитивно понятно, что данные параметры не являются значимыми для МДР. В свою очередь, значения параметров – конечный радиус R_e , процент ЧГП ( N_cr ) и число итераций, на которые частица из группы ЧЛП переходит в группу ЧГП ( H ), варьируются, так как они напрямую связаны с объектом исследования и являются ключевыми в МДР. Поэтому для оценки влияния R_e , N_cr и Н на результирующее решение по трем критериям и совместного влияния всех параметров проводится полнофакторный эксперимент (ПФЭ). Исследование по критериям оценки проводится по результатам роения 50 роев ( N_n = 50 ), состоит из 5 независимых опытов для каждого из 8 различных условий. В итоге необходимо провести 2000 опытов, что позволит оценить устойчивость результатов и влияние случайных исходных данных на эффективность оптимизации.

При проведении ПФЭ оценка свойств МДР, по опыту проведенных исследований и сути решаемой проблемы, проводится по четырем важным и показателям:

• -    Е ({ a i }) , эффективность нахождения всех точек экстремума исследуемой области. Данный критерий характеризует метод применительно к многоэкстремальным задачам. Он формируется как относительное среднее количество экстремумов, найденных МДР, заранее известному количеству экстремумов исследуемой функции;

• -    S ({ a i }) , ресурс, который определяет минимальное количество итераций, необходимых для нахождения локального экстремума. Для данного исследования он вычисляется как среднее число итераций, за которое центр роя достигает области нахождения одного экстремума, относительно общего числа итераций локального поиска, N all = 200 ;

• -    А ({ a i }) , точность оценки величины экстремума, т.е. средняя оценка близости найденного значения оптимума к заранее известному при тестировании значению экстремума;

• -    Sg ({ a i }) , глобальный ресурс, определяет количество итераций, за которое будут найдены все экстремумы. Он вычисляется как среднее количество итераций, за которое центры множества роев достигли области нахождения всех экстремумов к числу найденных экстремумов.

При этом эффективность метода является ключевым критерием, а три остальных – вспомогательными и могут накладывать дополнительные ограничения на значения параметров, если они не противоречат результатам оценки по критерию E .

Пример 1. Исследование многоэкстремальной одномерной функции.

Для исследования выбрана следующая функция Нейдорфа, график которой изображен на рис.1:

, _х   (1 - x )² + 15sin(1,1 x + 2)

У (x ) = -—  ,      -----

-\j x + 0,5

Исследование функции проводится на интервале x е [ - 20,20] , где функция имеет 6 минимумов: (–13,72; 15,22), (–8,38; 9,03), (–2,83; 0,42), (2,04; –5,7); (7,64; 4,12) и (13,01; 10,42).

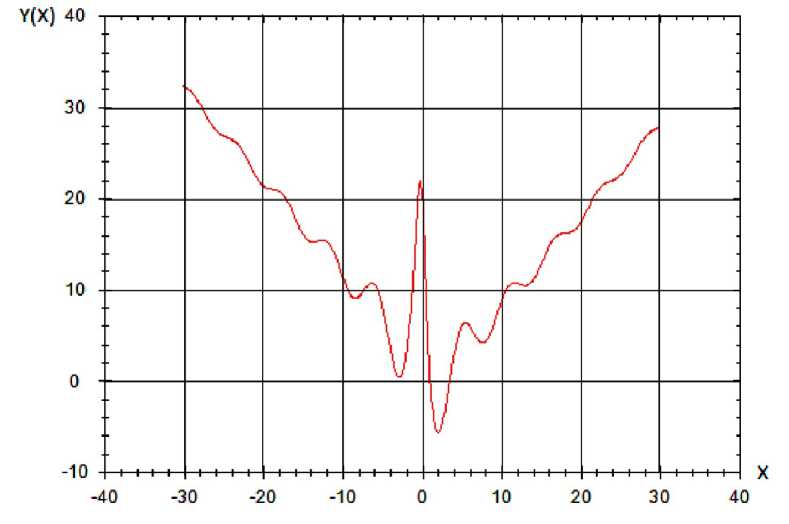
Рис.1. График функции Нейдорфа

Ставится задача нахождения экстремумов рассматриваемой функцией МДР. Для решения данной задачи были выбраны следующие параметры эксперимента: m = 50 частиц; R b = 2 (5 % от размера пространства поиска); X p = 0,06 , е p = 1 ; X t = 1 , е t = 0,7; | R_e | = 1,0,6,0,2 ; N cr = 10 %, 20 %, 30 % ; H = 5,15,20 .

Анализ результатов проведенного ПФЭ показывает, что для оптимальной эффективности МДР, т.е. нахождения всех экстремумов, необходимо установить максимальное значение параметров R_e и H . В свою очередь, оптимальные значения по другим критериям оценки получаются при минимальном значении параметра N_cr . Таким образом, в качестве эффективных значений факторов, при которых достигаются лучшие значения по всем критериям, выбираются: R e = 1 , N_cr = 10 и H = 20.

Для уточнения полученных значений параметров настройки проводится дополнительный ПФЭ с более узкими интервалами варьирования факторов. В качестве центра плана выбирается точка эффективных значений из предыдущего ПФЭ.

В результате происходит уточнение значений параметров настройки: R e = 1 , N_cr = 10 и H = 25. При данном наборе факторов критерии оценки имеют следующие значения: Е=1 (найдены все 6 экстремумов), S = 0,043, А = 2,77E–07, Sg = 0,0304.

Процесс выполнения МДР проиллюстрирован на рис.2. По оси Х откладываются итерации роения, а по оси Y – значения функции в центре роя на каждой итерации. Сплошными линиями обозначены траектории движения центров роев, которые в итоге нашли экстремумы, пунктирными линиями, в свою очередь, обозначены траектории роев, которые перешли в область локализации уже найденных экстремумов. Кроме этого представлена иерархия роев, т.е. показано, сумасшедшие частицы какого роя создали следующие рои.

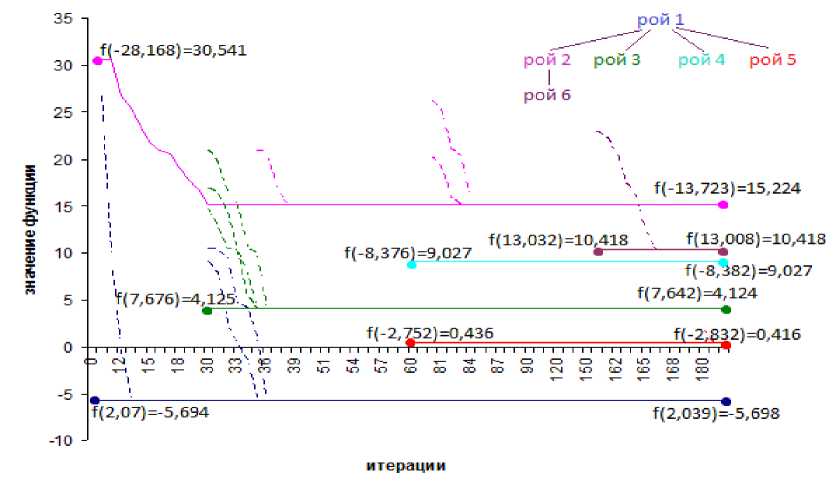
Рис.2. Графическое отображение процесса МДР

Для более наглядного представления траекторий движения роев, нашедших экстремумы, они строятся в логарифмических координатах по значению функции (рис.3).

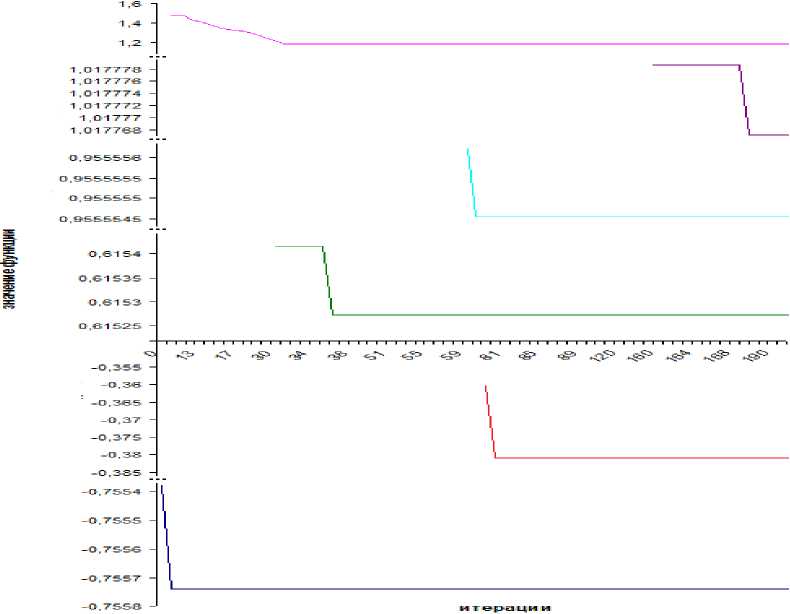
Рис. 3. Траектория движения роев в логарифмических координатах

Таким образом, показана эффективность применения МДР для нахождения экстремумов одномерной функции при определенных значениях параметров настройки.

Пример 2. Исследование двумерной функции Химмельблау (ФХ). Следующая по сложности тестовая многоэкстремальная функция Химмельблау. Она имеет четыре глобальных минимума, значения в которых равны нулю: (-2,8051; 3,1313), (-3,7793; -3,2832), (3,2), (3,5844; -1,8481). На рис.4 представлен график поверхности и линии уровня функции Химмельблау с отмеченными экстремумами.

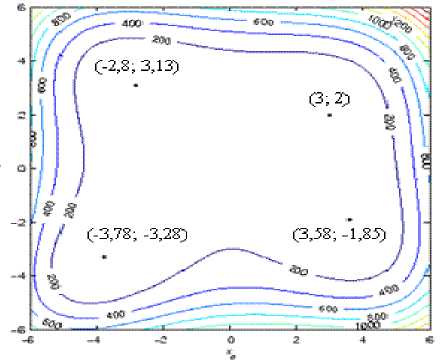
Рис.4. График поверхности и линии уровня функции Химмельблау

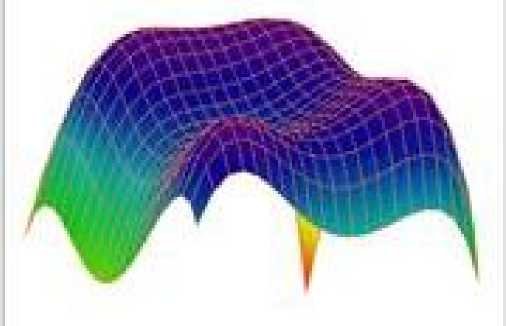
(перевернутый вид)

Для решения данной задачи выбираются следующие параметры эксперимента:

• -    фиксированные параметры: m = 800 частиц, R b = 6 , X p = 0,5 , е p = 0,05 , е t = 0,071 , X t = 0,71 , X с = 1 , е t = 0,08 ;

• -    варьируемые параметры: N cr = 10 %, 20 %, 30 %, R e | = 1,5; 1; 0,5 , H = 5,15, 20 .

В результате проведения серии ПФЭ получается вектор эффективных значений факторов: R e = 1,5 , N cr = 30 и H = 20. При этом получены следующие оценки критериев: Е = 1 (найдены все 4 экстремума), S = 0,025, А = 3,944, E = 31, Sg = 0,0071.

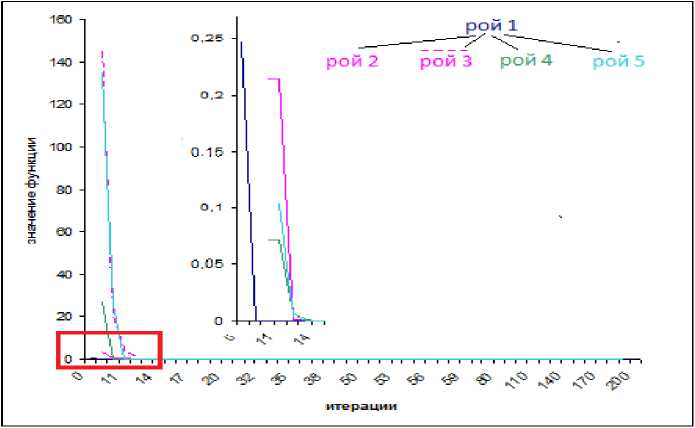
Рис.5. Процесс МДР для ФХ

Отображение процесса МДР представлено на рис.5. В связи с тем, что все экстремумы имеют нулевое значение функционала, то все центры роев находят одно и то же значение функции, но при различных значениях аргументов. В данном случае рой 1, 2, 4 и 5 нашли глобальные минимумы, а рой 3 переместился в область локализации экстремума, который был найден роем 2. Для большей наглядности процесс деления роев представляется в логарифмических координатах по оси «Значение функции» (рис.6).

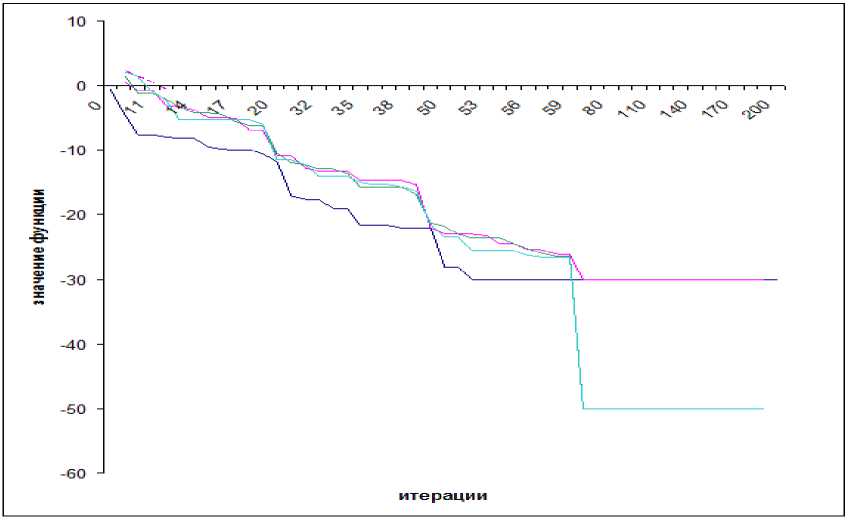
Рис.6. Процесс МДР для ФХ (в логарифмических координатах)

Заключение. Показано, что метод деления роя является эффективным инструментов для поиска множества экстремумов сложных функций, т.е. для решения многоэкстремальных задач. Эффективность МДР зависит от выбранных значений параметров настройки, которые могут отличаться при решении различных задач.