Решение некоторых проблемных задач механики движущихся масс

В классической механике законы сохранения массы и энергии трактовались как законы сохранения материи и движения (Фи-зический…,1983). Однако экспериментально наблюдаемая зависимость массы от скорости характеризовала не только количество материи, но и её движение. Понятие энергии подверглось изменению: полная энергия пропорциональна массе. Эта взаимозависимость массы и энергии привела к тому, что классическая механика была заменена релятивистской механикой, в которой объединены законы сохранения массы и энергии, существовавшие в классической механике по отдельности. В релятивистской механике невозможно характеризовать количество материи, не принимая во внимание её движения и взаимодействий   (Физиче- ский…,1983).

Цель исследования

Закон сохранения массы и энергии релятивистской механики является фундаменталь- ным законом физики. Он применим к любым физическим процессам независимо от природы сил, участвующих в них.

Целостность атомных ядер обусловлена сильным взаимодействием между нуклонами (ядерные силы); целостность атомов – электромагнитным взаимодействием; Солнечная система существует благодаря силам взаимного тяготения.

Исследования

Рассмотрим три простейшие реакции синтеза ядер (Трофимова, 2006).

• I.    6 Li + 2 H ^2 ⁴ He +₂ ⁴ He

(Qi = 22,4 МэВ), где 6Li – изотоп лития; 2H – изотоп водо рода (дейтерий);      – изотоп гелия; Q1 – количество теплоты, выделяемой в результате реакции.

Для этой ядерной реакции закон сохранения массы и энергии имеет вид (Трофимова, 2006)

E 1 = c²[(M 6 L + M 2 H ) -

-(M 4He+M 4He)]=c2ΔM1, где E1 – энергия, выделяемая в реакции; М – массы ядер; с – скорость света в вакууме; ΔМ – дефект масс, определяющий энергию связи нуклонов (Физический…,1983).

Проведем вычисления, пользуясь «Справочными материалами», приведенными в конце статьи:

M 6 + M 2   =8.02922457 а.е.м.;

M 4    + M 4    =8,00520651 а.е.м.;

Δ M 1 =0,02401806 а.е.м.     (1)

Энергия этой реакции

E 1 =Δ M 1 ∙c² =3,58449865∙10^-12Дж= =22,3725054МэВ = 22,4 МэВ.

Эта энергия равна количеству теплоты Q 1, выделяемой в результате реакции

E 1 = Q 1 .

Ядра изотопов ⁴ He в момент их образования образуют консервативную систему, т.к. отсутствуют внешние силы. Для такой системы количество теплоты Q 1 эквивалентно кинетической энергии этих ядер 2(Е к ) 4_{2 He}

Q 1 =2(Е к ) 4 _He = 2[(M ₂ 4 He · V ² ₂ 4 He )/2] =

= M 4 _He · V ² 4 _He .

Отсюда определим скорость ядра ⁴ He :

V ² 4^ = -Q1- =0,232230440 8 м =

2 He    _{M 2                 с}

4 ^He

= 0,23-10 8 м .

с

Ядро ⁴ He в этой реакции имеет достаточно большую скорость, поэтому его можно отнести к релятивистской частице. Но в этом случае масса m движущейся частицы зависит от скорости (Физический…,1983):

m 0

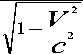
где m 0 – масса покоя частицы; V – скорость частицы; с – скорость света.

Изменения Δ m :

A m = m — m„ = m „ ( , ¹  . -1).

0     0      _V 2

1 ¹      2

c

Определим изменение массы ядра 4He при скорости V , принимая за массу покоя 42 He ядра гелия M = 42 He

=4,00260325 а.е.м.

A M 4 He = M 4 He ( ,        — 1) =

V 2 ⁴ He

1 ¹      c¹

=0,0120633 а.е.м. ^ 0,012 а.е.м.

Для двух ядер изменение массы удваивается:

2Δ M 4 He =0.024 а.е.м.

Это изменение масс равно дефекту масс Δ М 1 , найденному в соответствии с законом сохранения массы и энергии, т.е. дефект масс может быть найден из знания скорости ядер ⁴ He .

• II.   2 H + 3 H >. 4 He, + J n

Q2=17,4МэВ), где 3H – ядро изотопа водорода (трития);

1n – нейтрон; Q2 –количество теплоты, вы- деляемой в этой реакции.

Используя аналогию с предыдущими рас- четами и справочные материалы, находим: M2H +M 3H=5,0301510 а.е.м.;

M 4 He + M 1 =5,0112687 а.е.м.;

Δ M 2 =0,0182288 а.е.м.      (2)

Энергия этой реакции

Е 2 = Δ M 2 с² =2,81811661∙10^-12Дж=

=17,5893019МэВ = 17,6МэВ.

Эта энергия равна количеству теплоты Q 2 , выделяемой в данной реакции.

Ядро изотопа 4He и нейтрон 1n в момент их образования образуют консервативную систему. Для такой системы справедлив закон сохранения импульса (Физиче-ский…,1983):

V 4 He ∙ М 4 He + V ₁ 0 n ∙ М ₁ 0 n = 0. (3)

Из этого уравнения определим скорость нейтрона V ⁰ n через скорость ядра гелия ^{V 4} He ^:

V ₁ 0 n

V 4 M 4

He    He

.

M 1

1 _{0 n}

Количество теплоты, выделяемой в этой реакции, равно сумме кинетических энергий нейтрона (Ек) 0n и гелия (Ек) 4

Q2=(Ек) 10n +(Ек) 4He=

M 1 V ^{2 1} 0 n    M 4 V ² 4

=    0n      +    2He    2He .(5)

Подставим уравнение (4) в уравнение (5)

и найдем скорость V 0

что с высокой точностью соответствует дефекту Δ М 2 , найденному в соответствии с за-

M 4 _{2 He}V ² 4 _{2 He}

M 4 V ²

M (   ^{2 He}

^{10 n}          M 1

+------------ 0 n

M 4 _HeV ²

( 1+ ^> ) ;

M 1

¹ 0 ⁿ

^{V 4} He

2 QM 1

0 ⁿ

M 4 ( M 1 + M 4   )

₂ He      ₀ n       ₂ He

⁴ 2 He ) ²

коном сохранения массы и энергии.

III. 2 H+ 2 H ^ 3 ^Не + 0 n ( Q 3 = 3.3МэВ),

где ³ He - ядро изотопа гелия; Q 3 - количе-

=0,1306463^10 8 м = 0,13•10⁸ м .

сс

ство теплоты, выделяемое в этой реакции.

Используя аналогию с расчетами реакции I и «Справочные материалы», имеем

ЛМ з =0.00359319 а.е.м.;        (6)

Е з =ЛМ з с² =0,52373721 •10 ' ¹²Дж=

=3,26891085МэВ = 3,3МэВ.

Применяя закон сохранения импульса, по аналогии с расчетами реакции II определим

Кинетическая энергия ядра гелия

(Е к ) 4 He

M 4 V ² 4

₂ He     ₂ He

^{V 3} He

2 Q M

3       1 _{0 n}

M (M + M )

³ ₂ He      ¹₀ n         ³₂ He

=0,5672285640 ' ¹²Дж=

=3,54036253 МэВ = 3,54МэВ.

Из уравнения (3) найдем скорость V 0 _п :

V 0 _п =0,51843445-10 8 м = 0,52-10⁸ м .

сс

Кинетическая энергия нейтрона

M 1 V ² 1 0 ⁿ       0 ⁿ

(Е к ) 0 n

=2,2508871240 ' ¹²Дж = 14,05МэВ.

Сумма (Е к ) 0 „ + (Е к ) ₄ He = Q 2 =

= 17,59МэВ = 17,6МэВ.

Таким образом, энергия Е 2 , найденная из

закона сохранения масс, численно равна количеству теплоты Q 2 :

Е 2 = Q 2 .

Как для реакции I, найдем изменения масс нейтрона Л M 1 и ядра гелия Л M ₄„ , 0 n                                          2 He

учитывая их скорости:

Л M , = M 1 ( ,   ¹    - 1 ) =

¹0 ^{n               1} 0 ⁿ                          2

^{V 0} 1 n

• 1 -    _c 2

=0.01542908 а.е.м.;

Л М . = М ₄   (      ¹    - 1 ) =

• ⁴2 He         ⁴ 2 He                     2

V ₂ 4 _He

• 1    - _{c 2}

=0,003 80614 а.е.м.

Их суммарная масса

Л М, +Л М , =0,01923 522 а.е.м. =

• ¹ 0 n                ⁴2 He       ^,

=0,019 а.е.м.,

=0,07239963-10 8 м .

с

Соответственно

V 1 =0,21648423-10 8 м = 0,22-10⁸ м .

0 ⁿ                         _{с                с}

Для реакции III по аналогии с методикой, примененной в исследовании реакций I и II, найдем изменение масс ядра ЛМ 3 е и нейтрона ЛМ 1 и:

Л М   =0,00087988 а.е.м.;

3 He

Л М 1 =0,026466162 а.е.м.

1 _{0 n}

Их суммарная масса определена:

Л М₃   +Л М , =0,03 520042а.е.м. =

³ ₂ He           ¹₀ n

= 0,035 а.е.м., что с высокой точностью соответствует дефекту масс ЛМз, найденному в соответствии с законом сохранения массы и энергии.

В исследованиях реакций I, II, III использованы наши опубликованные работы (Петров и др., 2016а), (Петров и др., 2016б).

Рассмотрим закон сохранения массы и энергии при образовании атома водорода:

p+e ^ J H, где p - протон; e - электрон; 1H - атом водорода (протий).

Предположим, что электрон движется вокруг ядра (протона) по круговой орбите радиуса R 1 . При этом кулоновская сила взаимодействия между ядром и электроном сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона,

движущегося по окружности под воздействием кулоновской силы, имеет вид q2 e    niV2

4 πε R ² R ^.

^m 0     ,        V ²

1-c2

Отсюда кинетическая энергия электрона

E) . = m^ =^, 2    8 n^ R

Решение этого уравнения определяет, что скорость V =2,5963∙10⁸м/с.

Эта скорость близка к скорости света с .

где q e – заряд электрона; R 1 – радиус первой боровской орбиты (основное состояние); m e

Результаты

– масса электрона; ε – электрическая по-

стоянная.

Из уравнения (7), используя «Справочные материалы», найдем скорость электрона

V e =

qe

4 πε ₀ R ₁ m_e

=0.0218769∙10⁸ м .

с

Определим изменение массы электрона Δ m e при его скорости V e , принимая массу покоя m e =5.4858026∙10^-4 а.е.м.

A m e =m e (

-

V ²,

- 1) =

Скорости, близкие к скорости света, достигаются на ускорителях элементарных частиц. В реакциях синтеза (I), (II), (III) и при формировании атома водорода имеем уменьшения масс на дефект масс (1), (2), (6), (9). Следовательно, масса, как источник гравитационного поля, убывает. При скорости V =2,5963∙10⁸м/с масса, в обычном понимании как масса гравитационная, исчезает. В публикациях по адронному калайдеру при скоростях, близких к скорости света, адроны исчезают, хотя из общепризнанной зависимости

c

m =

m ₀

=1,460689∙108а.е.м.             (8)

1 -

Для атома водорода закон сохранения

V ² c ²

следует, что масса должна расти

массы и энергии имеет вид

E4=c2[(mp+me)- M 1 H ]=c2ΔM4, где mp – масса протона; M 1H – масса атома;

Δ М 4 – дефект массы.

Вычислим дефект массы, пользуясь «Справочными материалами»:

m p + m e =1,0078250526 а.е.м.;

M 1 H =1,007825036 а.е.м.;

Δ M 4 =1,426∙10^-8а.е.м.           (9)

Численное значение дефекта массы Δ М 4 (9) с достаточной степенью точности соответствует изменению массы электрона Δ m e , обладающей скоростью V e .

Из уравнения (8) найдем относительное изменение массы:

с увеличением скорости V и что это должно привести к появлению так называемой «черной дыры» с бесконечной массой. «Черная дыра» не появилась, а массы исчезли.

В нашей работе (Петров, 2011) проведены исследования движения планет Солнечной

системы исходя из зависимости изменения массы Δ m пл от скорости планет V пл. Получено

следующее соотношение:

^A m nn ₌V\ _ Ю пл R² пл m„   2 c²      2 c²

где ω пл – угловая частота вращения планеты вокруг Солнца; R пл – среднее расстояние планеты от центра Солнца.

В работе (Петров, 2013) приведены ре-

Δm m0         V2.

1- c

Из этого уравнения следует, что чем больше скорость V , тем больше ^m .

зультаты зависимости

Δ m_пл

от величины

1^0

. По данным вычислений построен гра- ^R пл

Определим, при какой скорости V дефект массы Δ m будет равен массе m e, т.е.

фик (рисунок).

Эту зависимость можно отобразить, используя уже сделанные вычисления (Петров, 2013), соотношением

Δ m_пл

m пл

7,398 ⋅ 10² R пл

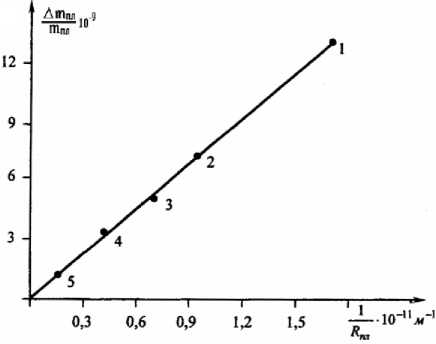
Зависимость Δm пл /m пл от 1/R пл : 1 – Меркурий; 2 – Венера; 3 – Земля; 4 – Марс; 5 – Юпитер

Используя (10), перепишем это соотношение:

7,398 ⋅ 10²   7,398 ⋅ 10²

R пл =           =           .

Δ m_пл / m_пл   V ² пл /2 c ²

Изменение массы Δ m пл будет равно массе планеты при её скорости, равной V =2,5963∙10⁸м/с.

Результаты вычислений дают значение

R пл =1972,963м.

Общая теория относительности определяет радиус «черной дыры» (радиус сферы Шварцшильда) для Солнца:

r ч.д . =

4 GM

3 c ²

=1968,739м,

где G - гравитационная постоянная; М с – масса Солнца.

Относительная погрешность двух вычислений:

^R пл ^{- r} ч . д .

^r ч . д .

⋅ 100% ≅ 0,2%

Исходя из наблюдений за движением планет Солнечной системы и используя эффекты общей теории относительности, мож- но заключить, что совпадение двух вычислений высокое.

Выводы

Исследования, проведенные с учетом сильных электромагнитных взаимодействий атома водорода, которые полностью соответствуют закону сохранения массы и энергии, позволяют утверждать, что этот закон справедлив для масс, вызывающих силы всемирного тяготения. А потому «черная дыра» связана не с массой, стремящейся к бесконечности, а с массой, равной нулю.

Справочные    материалы    (Физиче- ский…,1983)

M ⁶ L = 6,0151228а.е.м.;

M ² H =2,01410179а.е.м.;

M ⁴ He = 4,00260326 а.е.м.;

1 а.е.м. = 1,66056554·10^-27 кг;

c = 299792458м/сек ;

M ³ H = 3,01604928 а.е.м.;

M ¹ n = 1,00866501 а.е.м.;

M ³ He =3,01602932 а.е.м.;

M ¹ H = 1,007825036 а.е.м.;

m p = 1,007276470 а.е.м.;

m e = 5,4858026·10^-4а.е.м.;

1 эВ = 1,60218929·10^-19Дж;

G = 6,6720·10-11н∙м2/кг2;

M c = 1,989·10³⁰кг;

R 1 = 0,52917706·10^-10м;

ε = 8,85418782·10^-12ф/м;

q e = 1,6021892 ·10^-19кл