Решение обратной задачи гравиразведки для 2D призматических тел методом статистических испытаний

Обратная задача геофизики состоит в формировании модели геологической среды по результатам измерений геофизического поля при условии, что известен оператор прямого преобразования модели среды в соответствующие характеристики поля (Яновская, Порохова, 2004). Моделирование геологического строения по гравиметрическим данным, по Е. Г. Булаху, сводится к следующей задаче (Булах, 2010). На основании всех имеющихся сведений о геологическом строении площади исследований и петрофизической информации, а также с учетом результатов визуального анализа аномального поля и его трансформант осуществляется построение начальной схемы геологического строения. Местоположение и размеры геологических объектов характеризуются параметрами p 1 , p 2 , .. . p m , а значения плотности σ будем считать априорно известными. Таким

образом получим m -мерный вектор Р = { р 1 , р 2 , ..., р т } параметров среды . Можно говорить о функциональном пространстве Q, где каждой конкретной схеме соответствует своя точка Р : Р ∈ Q. Значения аномального поля можно представить как некоторый n -мерный вектор V = { v 1 , v 2 ,..., v n }. Пространство W объединяет различные совокупности V : V ∈ W.

Функциональные пространства W и Q связаны между собой. Установлено некоторое правило, по которому для значений параметров среды однозначно определяются значения аномального поля – алгоритм решения прямой задачи. В общем виде прямую задачу можно описать оператором L , который каждой точке пространства Q ставит в соответствие определенную точку из пространства W :

V =L( P ), V ∈ W, P ∈ Q. (1)

Обратная задача состоит в том, чтобы по заданным значениям компонент поля V определить вектор Р . Таким образом, обратная задача в операторной форме может быть записана так:

P = L^-1 ( V ), P ∈ Q , V ∈ W,     (2)

В общем, уравнение (2), использующее нелинейный обратный оператор L^-1 , не всегда имеет решение и требует привлечения дополнительных сведений, обеспечивающих устойчивость вычислительного процесса и геологическую содержательность результатов (Жданов, 2007). Таким образом, обратная задача гравиразведки (в наиболее важной для практики нелинейной постановке) состоит в нахождении пространственного распределения масс P по заданному гравитационному полю V этих масс.

В сложных физико-геологических условиях для решения обратной задачи (2) гравиразведки применяют метод подбора. Суть этого метода состоит в последовательном переборе уточняющихся геоплотностных моделей, расчете гравитационного эффекта от этих моделей с помощью решения прямой задачи (1), сопоставлении полученных значений модельного поля ^д мод с наблюденным полем Ад_н аб . Необходимым условием завершения итерационного процесса уточнения параметров модели является достижение высокой степени совпадения полей

^△днаб   △дмод || — £’ где £ > 0 - достаточно малая величина, соизмеримая с точностью определения аномалий Буге для использующейся гравиметрической съемки.

Метод реализуется в двух вариантах: неформализованный подбор, когда корректировка параметров модели выполняется вручную, на основании интуиции и опыта интерпретатора, и автоматизированный подбор, основанный на решении задачи многомерной оптимизации с ограничениями на вектор переменных P (Ягола и др., 2014). Также для этой цели могут использоваться методы случайного поиска, в частности – алгоритм с непрерывным самообучением, описанный в работе (Старостенко, 1978).

В данной статье будет рассмотрен простой по структуре алгоритм решения нелинейной обратной задачи гравиразведки для моногеничной аномалии, реализующий метод статистических испытаний (Монте-Карло). Данный алгоритм был разработан с целью обучения студентов и позволяет на практике получать необходимые представления о методе подбора, разрешающей способности гравиразведки, неоднозначности и неустойчивости решения обратной задачи, имитационном моделировании, модельных классах источников поля, множестве допустимых решений и т.п. Также будет представлен пример решения практической задачи – локализации рудоносной интрузии в Норильском районе с применением гарантированного подхода.

Краткая характеристика алгоритма

Метод Монте-Карло был предложен Станиславом Мартином Уламом (Stanisław Marcin Ulam) и Джоном фон Нейманом (John von Neumann) в 1949 г. для моделирования нейтронной диффузии в процессе работы в Лос Аламосе по «Проекту Манхэттен» («Manhattan Project»), реализующим программу США по разработке ядерного оружия (Каханер и др., 2001). Суть метода заключается в описании случайного процесса математической моделью, допускающей выполнение большого объема вычислений с различными входными данными, полученными путем генерации случайных чисел, с целью определения статистических характеристик рассматриваемого процесса (Буслен-ко, Шрейдер, 1961; Robert, Gasella, 2004). Прямое моделирование методом Монте-Карло какого-либо физического процесса подразумевает моделирование поведения отдельных элементарных частей физической системы (Rubenstein, Kroese, 2007).

В данном случае при решении 2D обратной задачи гравиразведки для одиночного изолированного аномалиеобразующего объекта, расположенного в однородной среде и обладающего эффективной плотностью О’, в роли элементарных частей системы выступают прямоугольные координаты его угловых точек. В алгоритме используются три модельных класса тел: горизонтальные пря- моугольные призмы, наклонные пласты (параллелограммы), горизонтальные четырехугольные призмы. Согласно теореме Новикова, решение обратной задачи гравиразведки в этих классах тел, звездных относительно заданной точки, при известной постоянной эффективной плотности является единственным (Блох, 2009). Однако на практике, в силу дискретного задания значений наблюденного поля Ад наб и ограниченной длины профиля наблюдений, эту возможность реализовать невозможно.

Во всех случаях вектор параметров модели имеет размерность т = 8 и выглядит одинаково: Р = {х 1, z 1 х ₂ , z ₂ , х ₃ z ₃ х ₄ , z₄ , }. Интерпретатором задается начальное приближение - вектор Р₀, затем выполняется внешний цикл, состоящий из K итераций, результатом которого является последовательность векторов Р 1, Р ₂ ,^,Р _К , обеспечивающих уменьшение невязки наблюденного и модельного полей в евклидовой метрике:

Е2=^(Ад наб -Ад мод )²/^ (3)

где N – число точек измерений поля. Степень близости полей также контролируется в метрике Чебышева: ЕМ = тах|Дд_на б — △ д_мод|, характеризующей максимальное по модулю различие амплитуды полей в точке наблюдений. Необходимым условием внешнего цикла вычислений является выполнение неравенства Е2^к+1< Е2^к , где к = 1, К - номер итерации. Рекомендуемое число итераций K составляет 20–50.

В пределах внутреннего цикла (отдельной итерации) генерируется M случайных векторов Р, при этом выполняется следующая последовательность операций:

• •    определяются минимальные и максимальные значения координат угловых точек уже имеющегося аномалиеобразущего объекта х^mln,z^mln,х^max,z^max (первоначально используется вектор Р₀);

• •    по имеющимся значениям х^т1П, z^mm, х^тах, z^max вычисляются координаты (х _ц ,z _ц ) центра прямоугольника, описанного вокруг этого объекта. Размеры этого

прямоугольника являются ограничениями при дальнейшем построении пробных тел (рис. 1);

• •    вычисляются новые координаты угловых точек для горизонтальной четырехугольной призмы с использованием восьми псевдослучайных чисел т, равномерно распределенных внутри интервала [0,1]: х = х ц ± т(х^тах-х^тт), z = z _ц ± _T(z^max-z^min) Для прямоугольной призмы достаточно случайным образом определить координаты верхней левой и нижней правой угловых точек, используя только четыре числа т, т.к. х 1 = х ₂ ,х ₃ = х ₄ , z 1 = z ₄ ,z ₂ = z ₃ . Расчет горизонтальной и вертикальной мощности, а также угла падения наклонного пласта требует пяти псевдослучайных чисел т, т.к. в этом случае z 1 = z ₄ ,z ₂ = z ₃ , х ₄ — х 1 = х ₃ — х ₂ .

• •    выполняется решение прямой задачи гравиразведки для нового аномалиеобразующего тела по формулам Е. Г. Булаха (Булах, 2010) и вычисление невязки Е2^к по формуле (3);

• •    в случае, если полученная невязка полей Е^к< Е^к-1 , где k - номер текущей итерации, выполняется выход из внутреннего цикла. При Е^к > Е^к-1 осуществляется переход к началу цикла. Число M (количество пробных тел) задается пользователем и обычно составляет от 10² до 10⁵.

Следует добавить, что данный алгоритм во многом базируется на положениях интерактивного динамического моделирования двумерных плотностных и магнитоактивных разрезов INTERACT (Гольцман, Калинина, 1991). Его прообразом является ранее предложенная более сложная вычислительная схема (Долгаль, Шархимуллин, 2011), впервые использующая построение функции локализации.

Программа PODBOR_ST и результаты имитационного моделирования

Алгоритм был реализован в виде программы PODBOR_ST, написанной с исполь-

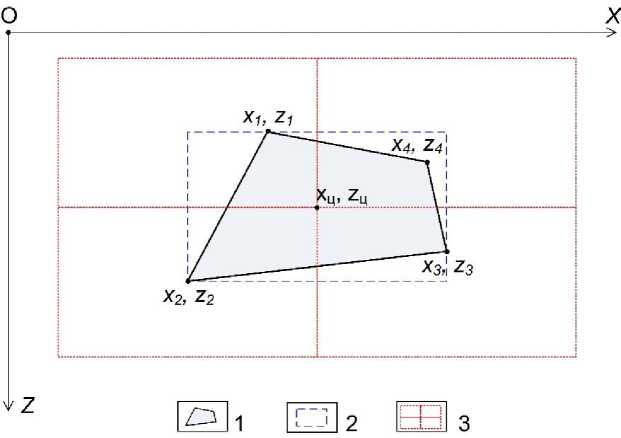
Рис. 1. Схема, поясняющая алгоритм решения обратной задачи гравиразведки в классе 2D горизонтальных четырехугольных призм: 1 – аномалиеобразующий объект; 2 – описанный прямоугольник; 3 - четыре подобласти, в пределах которых определяется местоположение угловых точек нового объекта

зованием объектно-ориентированного языка программирования Delphi.

Перед решением обратной задачи необходимо выбрать модельный класс тел, задать количество точек измерений N, шаг между точками (в км), эффективную плотность тела (в г/куб. см), требуемое количество итераций K, число случайных векторов M, а также вы-ключить/включить опцию «Случайность». Последнее означает использование/отказ от использования одной и той же последова- тельности псевдослучайных чисел {т}, имеющей очень большую периодичность. В случае отказа включается процедура RANDOMIZE, что иногда помогает улучшить результаты случайного поиска. Затем вводятся имя DAT-файла, содержащего порядковые номера, высотные отметки и значения аномального гравитационного поля в точках наблюдений, а также имя BLN-файла для начального приближения моделируемого объекта.

Номер итерации

“Число точек N [26

Чис ло итераций К |25

Шаг по профилю

Чис ло векторо в М |1000

ЭФФ. плотность

Случайность (Г OFF С ON

Модельный класс тел (• ■ прямоугольная призма С - наклонный пласт С • четырехугольная призма

Рис. 2. Главное окно программы PODBOR_ST

Алгоритм не требует «хорошего» начального приближения и характеризуется высоким быстродействием: при N = 26, K = 25, M = 10000 время решения задачи на компьютере с процессором Intel(R) Core(TM) i7-4710HQ с тактовой частотой 2.50GHz составляет около 3 с.

Выходными данными программы являются BLN-файлы, содержащие модели источников, полученные на каждой итерации и DAT-файлы полей, созданных этими источниками. Также записывается текстовый файл протокола расчета, в каждой строке которого содержатся номер итерации k , значения функционалов F2 и FM , прямоугольные координаты центра описанного прямоугольника х ц ,г ц . Варьируя значениями К и М, практически в любых случаях удается достигнуть необходимой точности решения поставленной обратной задачи.

Известно, что имитационное моделирование является основным инструментом тестирования компьютерных технологий решения обратных задач геофизики. Согласно В. Н. Страхову (Страхов, 2005), оно заключается в следующем:

• 1.    Создание набора адекватных реальности числовых моделей изучаемого фрагмента геологической среды или геологического объекта;

• 2.    Расчет аномальных эффектов для каждой из построенных моделей путем решения прямой задачи геофизики;

• 3.    Осложнение полученных модельных полей искусственной помехой с некоторыми ожидаемыми на практике параметрами;

• 4.    Решение целевых задач интерпретации для полученного набора данных, имитирующих изучаемый фрагмент среды или объект;

• 5.    Сопоставление результатов, полученных для набора различных моделей и помех во входных данных

• 6.    Оценка на качественном уровне надежности и точности решения поставленной задачи.

Решение обратной задачи программой PODBOR_ST проведено с использованием весьма «плохого» начального приближения (резко отличающегося по форме, размерам и местоположению от истинного источника аномалии) в классе четырехугольных призм произвольного сечения. После выполнения 25 итераций при числе случайных векторов M = 25000 построена модель источника, перекрывающая более 80% площади сечения истинного тела (рис. 3). Достигнута высокая степень совпадения наблюденного и модельного полей. Ход итерационного процесса представлен на рис. 4.

Для других модельных классов тел алгоритм также позволяет получить вполне удовлетворительные результаты моделирования (квазирешения задачи [0] ), приведенные на рис. 5. Начальное приближение и параметры решения задачи были аналогичными ранее приведенному примеру.

Для оценки помехоустойчивости алгоритма были получены три новых решения обратной задачи по осложненному нормально распределенной помехой полю Ад _наб . Помеха δ , обладающая нулевым математическим ожиданием и среднеквадратическим отклонением 0.2 мГал, была получена процедурой RANDN(0, 0.2) в программе SURFER 13.0 (Golden Software Inc). Полученные результаты свидетельствуют о достаточно высоких возможностях работы алгоритма в условиях случайных помех (рис. 6). Все построенные модели могут использоваться для локализации возмущающего объекта, значения невязки наблюденного и модельного полей соизмеримы с уровнем наложенной помехи δ (табл. 1).

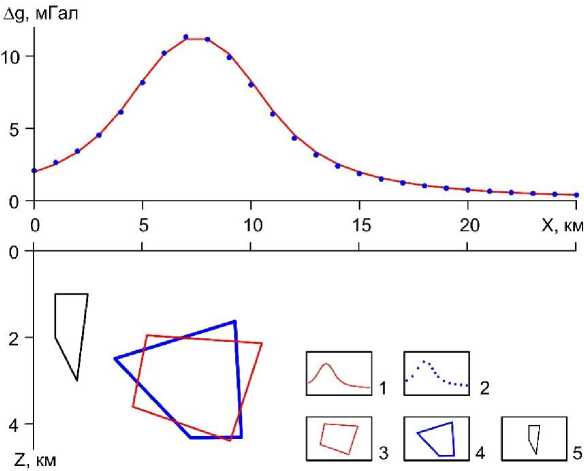
Рис. 3. Решение обратной задачи в классе четырехугольных призм произвольного сечения: 1 – наблюденное поле; 2 – модельное поле; 3 – возмущающий объект; 4 – подобранная модель источника; 5 – начальное приближение

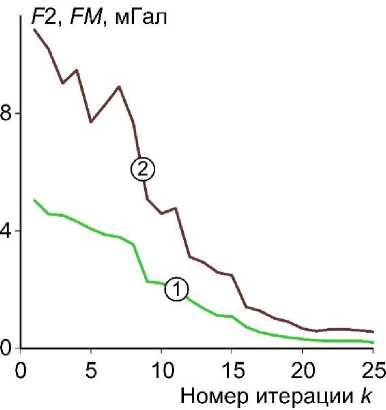
Рис. 4. Графики изменения невязки F1 (1) и FM (2) в процессе решения обратной задачи

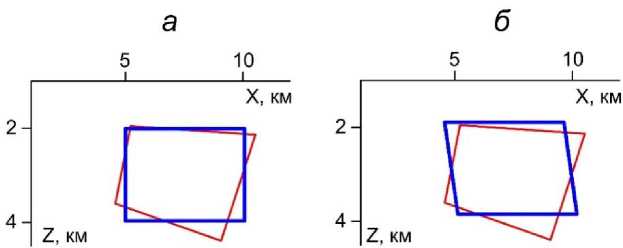
Рис. 5. Результаты решения обратной задачи в классах прямоугольных призм (а) и наклонных пластов (б). Условные обозначения даны на рис. 3

Таблица 1. Показатели точности решения обратной задачи гравиразведки с использованием точных и осложненных помехой значений наблюденного поля

Модельный класс	Наличие помех δ	Показатели точности, мГал
		F2	FM
Четырехугольная призма	нет	0.05	0.15
	да	0.20	0.54
Прямоугольная призма	нет	0.06	0.13
	да	0.24	0.57
Наклонный пласт	нет	0.09	0.19
	да	0.20	0.59

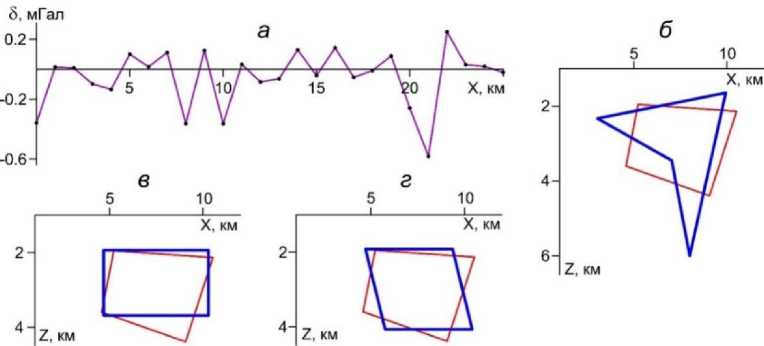
Рис. 6. График случайной помехи (а) и результаты решения обратной задачи по осложненному помехой полю в классах: четырехугольных призм (б); прямоугольных призм (б); наклонных пластов (г). Условные обозначения даны на рис. 3

Важнейшим моментом при использовании метода является выбор числа статистических испытаний М X К. Для схемы независимых испытаний погрешность метода Δ убывает пропорционально (М X К)-0 5, т.е. весьма медленно [0]. Экспериментальные результаты, приведенные в табл. 2, позволяют предположить, что в большинстве случаев для решения обратной задачи гравиразведки в программе PODBOR_ST достаточно выбрать число М X К = (1 — 5) X 106. При низком уровне помех δ выполнение этого условия может обеспечить получение невязки (3) ∼(1–2)% от максимальной амплитуды интерпретируемой аномалии.

Таблица 2. Зависимость точности и времени решения обратной задачи гравиразведки от числа испытаний M при выполнении 40 итераций

№ /№	M	Точность решения, мГал		Время счета, с
		F2	FM
1	500	0.25	0.65	2
2	1000	0.25	0.65	4
3	5000	0.15	0.45	14
4	10000	0.14	0.35	22
5	50000	0.09	0.22	36
6	100000	0.08	0.18	63
7	500000	0.06	0.11	782
8	1000000	0.05	0.13	1352

Решение практической задачи: гарантированный подход

Традиционно оценка качества количественной интерпретации в гравиразведке базируется на оценке степени перекрытия вертикальных сечений (для 2D обратной задачи) или объемов (для 3D обратной задачи) модельного S* и истинного S аномалиеобразующих объектов:  ||S* — S||. Модельный объект S* в данном случае представляет собой один элемент из множества Q допустимых решений обратной задачи, удовлетворяющих априорной информации и обеспечивающих выполнение условия F2 < £, где s – малая величина, сопоставимая с точностью интерпретируемой гравиметрической съемки. Однако существуют непосредственные оценки истинного решения обратной задачи, не связанные с одним из допустимых вариантов интерпретации – гарантированный подход (Балк, Долгаль, 2020).

Для обратной задачи гравиразведки рудного типа к этому типу оценок можно отнести минимальную и максимальную области геологического пространства D 1 и D ₂ , обеспечивающие неулучшаемые включения:

D2c ScDt.    (4)

Множество «пересечения решений» обратной задачи D 2 будет давать фрагмент, гарантировано принадлежащий возмущающему объекту S , а множество «объединения решений» позволяет оконтурить область пространства D 1 , в котором может содержаться искомый объект. Предложенный алгоритм позволяет осуществлять построение множества Q различными способами: использованием различных начальных приближений (векторов Р₀); генерацией разных последовательностей случайных чисел {т_п}; изменением модельного класса тел. Рассмотрим пример локализации рудоносной интрузии габбро-долеритов по данным крупномасштабной гравиметрической съемки, выполненной над месторождением медно-никелево-платиновых руд Норильск-1 (рис. 7). Гравитационная аномалия Дд_на6, полученная после исключения линейного регионального фона, предположительно обусловлена рудоносной интрузией базит-гипербазитового состава, обладающей эффективной плотностью 0.25 г/см ³ по отношению к вмещающим породам туфолавой толщи. Точность выполненной гравиметрической съемки составляет 0.15 мГал.

дд, мГал

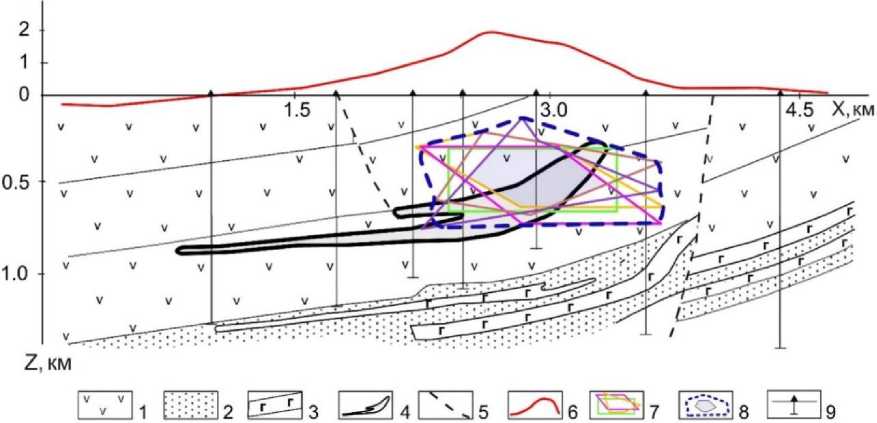
Рис. 7. Результаты количественной интерпретации аномального гравитационного поля над месторождением медно-никелево-платиновых руд Норильск-1: 1 – породы туфолавовой толщи; 2 – отложения тунгусской серии; 3 – силлы габбро-долеритов; 4 – рудоносная интрузия; 5 – дизъюнктивные нарушения; 6 – локальная составляющая гравитационного поля в редукции Буге; 7 - частные решения обратной задачи гравиразведки; 8 - области D 1 (синий пунктир) и D 2 (полупрозрачная заливка); 9 - буровые скважины

На рис. 7 показаны пять частных решений обратной задачи, полученных программой PODBOR_ST с использованием трех модельных классов тел, при K = 40, M = 25000, во всех случаях финальные значения F2 <  0.15 мГал. Осуществлен синтез этих решений на основе гарантированного подхода (4). Выход за пределы области D 1 маломощных субгоризонтальных фрагментов рудоносной интрузии в левой части геологического разреза объясняется их очень слабым гравитационным эффектом. Смещение области D ₂ в верхнюю часть разреза относительно фактического положения интрузии можно объяснить неучтенным в интерпретационной модели ореолом надинтрузивного уплотнения вмещающих эффузивных пород. Тем не менее очевидным фактом является возможность гарантированного подсечения интрузии при разбуривании области D₂ до глубины 600–800 м.

Следует добавить, что для более достоверной локализации областей D 1 и D ₂ требуется синтез около 300–1200 решений обратной задачи, что может быть реализовано на современных компьютерах без существенных затрат времени.

Заключение

Разработан и программно реализован алгоритм приближенного решения нелинейной обратной задачи гравиразведки для 2D аномалиеобразующих призматических тел четырехугольного сечения методом статистических испытаний.

Используется генерация случайных многомерных векторов координат угловых точек модели, в процессе анализа пробных решений контролируется величина невязки наблюденного и модельного полей в евклидовой метрике. Каждое последующее приближение строится с учетом ранее полученной информации о координатах центра тяжести и размерах ранее построенного возмущающего объекта, содержащейся в параметрах описанного прямоугольника. Тестирование показало достаточно высокую точность, помехоустойчивость и быстродействие программы PODBOR_ST.

Данный алгоритм прост, интуитивно понятен и легко воспринимается студентами в процессе обучения. Лабораторные работы, выполняющиеся студентами на протяжении нескольких лет с использованием программы PODBOR_ST, позволяют познакомиться с методикой имитационного моделирования и на практике закрепить основные понятия из области теории решения некорректных задач математической физики. Важной особенностью программы как средства обучения является уникальный характер каждого вычислительного цикла, позволяющий судить о самостоятельном получении имеющихся результатов расчета. Программа также позволяет осуществлять решение ряда практических задач и может эксплуатироваться в производственных организациях.

Метод статистических испытаний может успешно использоваться в качестве инструмента построения конечных множеств допустимых решений обратной задачи рудного типа с целью применения детерминированных (гарантированный подход) и статистических (аддитивные технологии) способов количественной интерпретации.