Решение оптимизационных задач при формировании стратегий разработки группы газовых месторождений

В отделе математических методов регионального программирования Вычислительного центра, им. А. А. Дородницына. ФИЦ «Информатика, и управление» РАН в течение многих десятилетий ведутся работы по решению задач комплексного освоения территорий. В рамках концепции регионального программирования [1] были разработаны модели, методы и алгоритмы, созданы программные комплексы для решения задач перспективного планирования газо- и нефтедобывающих регионов, проектирования генеральных схем обустройства, нефтяных и газовых месторождений и т. д.

В частности, была, разработана. Система, перспективного планирования добычи газа. (СПДГ) [2], предназначенная для формирования долгосрочных планов разработки группы газовых месторождений и обеспечивающая расчет объемов добычи газа, и основных технико-экономических показателей добычи в динамике на. долгосрочную перспективу. Система, многократно использовалась при расчетах долгосрочных планов добычи газа, по различным объектам газодобычи: группам месторождений Северо-Тюменской газоносной провинции, Восточной Украины, шельфа Черного моря, Ямбургскому и Оренбургскому месторождениям и т.д.

Необходимость анализа долгосрочных перспектив добычи газа и экономической эффективности добычи для принятия стратегических управленческих решений по освоению новых газодобывающих регионов страны, в первую очередь на Востоке и Крайнем Севере, обусловливает актуальность перспективного планирования и прогнозирования в газовой отрасли. Несколько лет назад была разработана Система моделирования и оптимизации добычи газа (СМОД) [3, 4]. Система является дальнейшим развитием системы СПДГ в современных условиях и обеспечивает формирование стратегий разработки группы газовых месторождений на основе совместного использования имитационного моделирования, дискретной и многокритериальной оптимизации.

Работа обеих систем основана на аппроксимирующей имитационной модели группы месторождений и многошаговом алгоритме [2], который по минимальной входной и управляющей (план добычи по группе месторождений, порядок ввода месторождений в эксплуатацию) информации позволяет распределить планируемую добычу газа в динамике между месторождениями. Алгоритм для каждого года пытается выполнить план добычи, «набирая» его из объемов добычи отдельных месторождений, вводимых в заданном порядке. Для полученных объемов добычи газа в динамике формируются многочисленные технологические и экономические показатели добычи и транспорта газа.

План добычи является важнейшим управлением для модели группы газовых месторождений, поскольку именно он определяет распределение и динамику добычи по отдельным месторождениям и, соответственно, все остальные показатели разработки группы месторождений. Если при централизованном планировании целью функционирования группы месторождений являлось выполнение заданного плана добычи, часто заданного без учета экономической эффективности и ограничений на ресурсы, то в условиях рыночной экономики план добычи нельзя считать заданным, то есть возникает задача формирования и оптимизации стратегий разработки группы газовых месторождений. Кроме того, оставаясь в рамках только имитационной модели, невозможно оценить экстремальные варианты планов, часто представляющие наибольший интерес.

Задача нахождения наилучшей стратегии разработки для группы месторождений по своей сути является многокритериальной. Важнейшим критерием является накопленная добыча газа (извлекаемые запасы газа); максимизация накопленной добычи — это и удовлетворение растущего спроса на газ, и валютная выручка, и эффективное использование запасов. С другой стороны, чистая стратегия максимизации накопленной добычи является весьма затратной (большие объемы буровых работ) и неэффективной с точки зрения транспорта газа.

Предлагается искать приближенное решение оптимизационной задачи в дискретной постановке с использованием методов дискретной оптимизации, причем искать не только оптимальное решение для заданного критерия, но и множество близких к нему решений [5]. Для каждого такого решения по результатам моделирования определяются значения дополнительных критериев, что позволяет осуществлять многокритериальный выбор стратегии для реализации.

Постановка задачи

Для сложных систем в настоящее время часто отказываются от аналитических методов исследования и поиска оптимума с переходом к комбинаторным методам оптимизации. При этом нередко используются сеточные методы [6], когда значение функции от многих переменных вычисляется и оптимизируется лишь в точках некоторой сетки, покрывающей область изменения значения каждого параметра. Очевидно, что для сеточных методов невозможно оценить абсолютную погрешность алгоритма поиска приближенного решения.

Приведем постановку и решение задачи оптимизации накопленной добычи газа для группы газовых месторождений. Классическая кривая объема добычи газа на месторож- дении (группе месторождений) имеет регулярный вид и состоит из трех участков: а) выход на «полку» — уровень постоянной добычи (УПД) как монотонно неубывающая функция; б) нахождение на УПД; в) падение добычи (монотонно убывающая функция). При заданных характеристиках каждого месторождения (запасы, полки, дебиты и т.д.) управлениями для группы месторождений являются план добычи по группе и последовательность ввода месторождений в эксплуатацию. В соответствии с имитационной моделью [2] поведение каждого месторождения группы и всей группы определяется траекторией выхода на УПД и величиной УПД для группы.

Исходная непрерывная задача оптимизации накопленной добычи сводится к дискретной задаче за счет введения равномерной сетки, которая покрывает область выхода траекторий плана добычи по группе месторождений на уровень постоянной добычи. На координатной плоскости «Время/План добычи» определяется область D выхода траекторий планов добычи газа Р (t) на УПД. Это прямоугольная область, где правый верхний угол имеет координаты ( T_maxi Р_тах), г де T_max — максимально возможное время выхода добычи по группе на УПД, a Pmax — максимально возможный УПД для данной группы месторождений.

Область D покрывается равномерной сеткой с параметрами (п,т) п — количество узлов по оси абсцисс, а т — по оси ординат. Предлагается искать приближенное оптимальное решение задачи на некотором конечном подмножестве G допустимых траекторий планов добычи Р *(t), проходящих через узлы равномерной сетки.

Любая траектория Р * (t) может быть задана на сетке целочисленным вектором плана у = (уі , у2 ,..., у _п ). Здесь yi — номер узла сетки по оси ординат, соответствующий узлу сетки с номером г по оси абсцисс при прохождении траектории плана Р *(t) через точку (г,уг ) сетки, где г = 1,п, уг = 1,т. На рис. 1 показаны векторы у^ = (2,4, 5, 5) и у^в = (1,1, 2,4) при п = 4, т = 5 и нижнем о граничении Pmin (t) на траектории планов.

Любой вектор плана является кортежом декартова произведения (Go )^п, Go = {1,2, ...,т}. В силу условия Р (t) 6 Р (t + 1), то есть технологически обусловленного неубывания планов добычи, среди всех кортежей данного декартова произведения рассматриваются лишь кортежи с неубывающими значениями. Это — элементы множества G С (Go)^п — векторы планов, для которых yi 6 Уг+һ г = 1, п — 1.

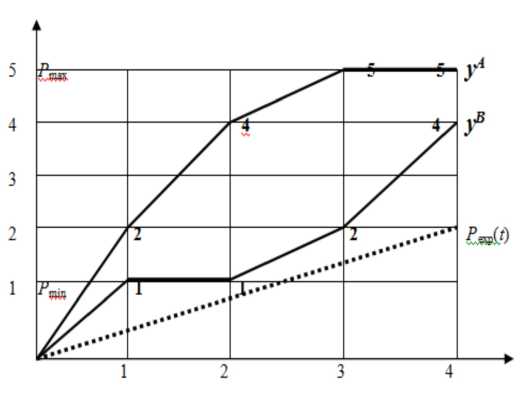
Рис. 1. Область G и векторы траекторий планов добычи

С учетом сказанного выше задача оптимизации накопленной добычи для группы месторождений в дискретной постановке ставится следующим образом.

Пусть G — конечное множество всех допустимых векторов планов для сетки с параметрами (п,т), G С (Go)п, Go = {1, 2,..., т}. Пусть на G определена функция /(у), у ЕС, характеризующая эффективность соответствующего вектору у плана добычи по группе месторождений Р* (t), то есть накопленную добычу по группе месторождений за заданный период времени Т.

Необходимо найти такое решение у* G G, что

/ (у*) = max / (у), yeG а также множество решений N, близких к оптимальному, такое что

/(у) > /(у*) - R, у G N С G, где / — функционал накопленной добычи по группе месторождений, a R — заданная ве личина.

Для решения оптимизационной задачи используется модифицированный метод ветвей и границ (ММВГ) [7] позволяющий находить не только оптимальное, но все близкие к нему по значению функционала накопленной добычи решения из N [8, 9]. Как известно, при использовании МВГ основной проблемой является определение способа разбиения на подмножества и нахождение оценок подмножеств разбиения. При этом условием применимости МВГ при решении задач максимизации является нахождение такого способа разбиения на подмножества множества исходных вариантов и такой верхней оценки этих подмножеств разбиения, которая бы не возрастала по мере дальнейшего разбиения.

Для сетки с параметрами (п, т) будем строить подмножества разбиения следующим образом. Каждое подмножество разбиения Gi,j, г = 1,п, j = 1,т, будет содержать такие вектора планов, что для любых у¹, у² G Gt,j (индеке г увеличивается с конца планового периода):

• -    у1 = у2 у^у ² > ^{j П}Р^{И t}< ^г

• -    у1 = у² = Р

• — у1, у² произвольны, у1, у2 6 j при г < t 6 п.

Разбиение множества решений G на подмножества при реализации ММВГ производится справа налево — от конца временного периода выхода на УПД. Тогда в каждом подмножестве Gi,j будут находиться векторы планов, у которых правые части совпадают, а левые — не определены. То есть элементами каждого подмножества являются планы добычи с одинаковым УПД, но с разными годами и разными траекториями выхода на УПД.

Был разработан алгоритм, обеспечивающий систематическую генерацию всех неубывающих кортежей декартова произведения — векторов планов, удовлетворяющих заданным ограничениям; алгоритм также позволяет по номеру варианта восстановить вектор плана и рассчитать полный комплекс показателей для данного варианта плана добычи. Алгоритм работает по принципу «счетчика такси»: каждый раз при переходе к новому варианту уве личивается на единицу самый последний элемент вектора плана у.

Данная задача дискретной оптимизации является неполиномиальной с оценкой О(т^п).

Оценка может быть существенно улучшена: мощность множества х_т,_п допустимых решений G для задан ной сетки (п, т) с учетом неубывания значений векторов планов может

быть оценена [5] с помощью рекуррентных соотношений вида х_т,_п

хт,п

Ет к=1 хк,п-1-

— ^хт,п- 1 + ^хт- 1,п

ИЛИ

Область допустимых решений G можно еще более сузить за счет введения следующих

ограничений на допустимые варианты планов:

е эксперт может задать верхние L1 (t) и нижние L2(t) ограничения на возможные траектории выхода плана добычи на УПД;

• •    L3(t) задает максимально крутой выход плана добычи по группе на УПД с учетом заданных максимальных допустимых приростов годовой добычи для каждого месторож

дения;

• •    L⁴(t) определяется как сумма полок всех месторождений группы; очевидно, что Р (t) 6 L4 (t);

• е    L⁵(t) отражает возможность наличия накопленной добычи на начало планового периода; очевидно, что Р (t) > L⁵(t) в силу неубывания планов добычи при выходе на УПД.

Кроме того, обеспечивается:

• •    округление в ту или иную сторону значений ограничивающих траекторий L¹ (t) — L5 (t) до значений в ближайших узлах сетки;

• •    автоматическое построение итоговых верхнего и нижнего ограничений на планы добычи L^max (t) = min(L1 (t), L³(t), L⁴(t)), L^min(t) = max(L²(t),L⁵(t)), t = 1,n.

Верхние оценки подмножеств разбиения

Пусть Q _y (t) — функция добычи газа по группе месторождений для плана у G G, тогда накопленная добыча на [0,Т] есть f(у) = /^ Q_y(t)dt. Определим оценочную функцию добычи Qy (t) и оценочную функцию накопленной добычи f* (у) = J^ Q* (t) dt так, чтобы для любого плана добычи у G G и любого t G [0,Т] выполнялись условия Qy(t) >  Q_y (t), f* (у) > f(у)

Qy (t) = Q_y (t) до момента, начала, падения добычи по группе при УПД р;

Qy (t) = Р на этапе падающей добычи по группе.

Функции Q_y (t) и Qy(t) приведены на рис. 2, причем Qy (t) выделена утолщенной линией, а для динамики добычи Q_y (t) отмечены три этапа: 1 — этап роста добычи (выхода на УПД), 2 — этап постоянной добычи при УПД р и 3 — этап падения добычи.

Для оценочной функции добычи Q* (t) также определяется оценочная функция накопленной добычи f* (у) = ]^q Q* (t) dt. Заметим, что f* (у) = f(у), если соответствующий вектору плана у план добычи по группе месторождений полностью выполняется до конца планового периода.

Поскольку для любого плана у G G и любого t G [0,Т] справедливо Qy(t) >  Q_y (t), то очевидно, что f* (у) = J0f Qy (t) dt >  J^ Q_y (t) dt = f(у), то есть функция f * (у) является верхней оценкой накопленной добычи газа f (у ).

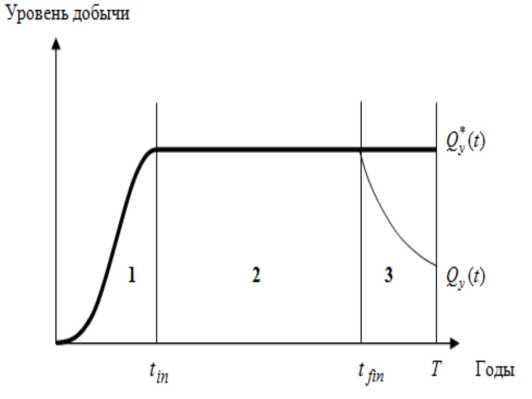
Рис. 2. Динамика добычи газа по группе месторождений

На множестве G вводится отношснис порядка. >: у ¹ >  у ² (у¹ доминирует у ²), у ¹, у² G G, если у¹ > у², г = 1,п, но существует хотя бы один номер г* такой, что у¹* = у²*. Доказывается, что оценочная функция f * (у) монотоина по у, то есть из у¹ >  у ², у ¹, у² G G следует f * (у¹) >  f * (у²) [5].                                                                        ____

В качестве верхней оценки g(Gi,j ) произвольного подмножества разбиения G^ г = 1,п, 3 = 1,т, предлагается использовать функцию накопленной добычи f * (у) для так называемого доминирующего вектора плана ущ G Gi,j такого, что ему соответствует самая верхняя траектория выхода плана добычи на УПД среди всех траекторий подмножества Gij, то есть g(Gi,j ) = f * (Уi,j), г де Уi,j >  у для любого у G Gij и у^ G Gij.

Если разбить произвольное подмножество Gi,j н a j подмножеств G_i+1,₁, G_i+₁,₂,• • •, G^yj, то верхняя оценка каждого к-го подмножества G^p^, к = 1,j, будет достигаться для доминирующего вектора плана ti+vj*, при этом t_i+1,j = j, j и g(G_i+1,j ) = g(G_id ). Так, на рис. 3 показаны доминирующие векторы планов для подмножеств разбиения Ga,5 для сетки с параметрами п = 6, m = 7.

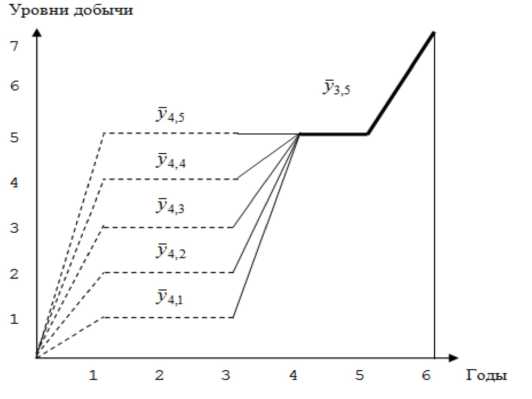
Рис. 3. Доминирующие векторы планов для подмножеств разбиения

Очевидно, что ti,j доминирует каждый из векторов ti+ЦАь то есть ti,j > д^+1^₁ к = 1, j, и траектории выхода планов добычи из Gi+p& на УПД лежат не выше траекторий планов из Gi,j, то есть по мере разбиения на подмножества траектории выхода планов добычи на УПД становятся все более пологими.

Невозрастание верхних оценок

Необходимым условием применения метода ветвей и границ при решении задач максимизации является невозрастание верхних оценок подмножеств решений по мере их дальнейшего разбиения.

Теорема. Пусть множество G_i+1p является подмножеством разбиения для Gy, то есть Gi+1p С Gi,j. Верхняя оценка подмножеств разбиения векторов планов не возрастает по мере разбиения, то есть

g(Gi+1,_k ) 6 g(Gi,j ),      к = T?j.

Фактически требуется доказать следующие три утверждения.

• 1.    Функция g вида g(Gi,j ) = /* (ti,j ) является оценкой для подмножества разбиения Gi,j, то есть максимально соответствует каждому исходному функционалу и быстро рассчитывается.

• 2.    Оценка g(Gi,j ) является верхней оценкой, то есть g(Gi,j ) > /(у) для любого у G Gi,j.

• 3.    Оценка g(Gi,j ) не возрастает по мере разбиения на подмножества, то есть g(Gi₊i,k ) 6 g(Gi,j ) при Gi₊i,_k С Gi,j для любого к = 1J.

Пусть G* С G — произвольное подмножество разбиения, t G G* — доминирующий вектор плана для G* и, по определению верхней оценки, g (G*) = /* (ц). Для расчета /* (t) не требуется рассчитывать динамику добычи для каждого месторождения группы, используя модель группы месторождений. На самом деле, поскольку разумный план добычи по группе всегда выполняется на этапе роста добычи, то:

/1 (t) = Тл^і tA где d — шаг сетки по оси ординат — на этапе роста добычи до момента времени п < Т;

/* (t) = tn(Т — п) = р(Т — п) — на этапе постоянной добычи.

При этом /* (t) и / (t) отличаются друг от друга лишь на этапе 3 падения добычи по группе месторождений, а для хороших планов данный этап может вообще отсутствовать.

Поэтому оценка g(G* ) = /*(t) = /* (t) + /2*(j рассчитывается достаточно быстро.

По определению верхней оценки g(Gi,j ) = / *( у і, ), а в силу монотонности оценочной функции из гу, > у следует, что / *(yt,j ) > / *(у) для любого у G G_i,j. Но по построению функции /*(у) для любого у G Gi, справедливо /*(у) > /(у), поэтому g(Gi,j) >  /(у), то есть g(Gi,j ) является верхней оценкой для произвольного подмножества разбиения G i,j.

По определению доминирующего вектора плана, Уг+₁,k G G_i+_i,k и 5i+i,k > у для любого у G Gi+i,k, к = 1,j. Так как Gi+i,k С Gi,j, то поэтому и yi+1,k G Gi,j. А поскольку по определению доминирующего вектора плана гу, G G_i,j и уу, > у для любого у G G_i,j, то также и щ, >  Si+ik

В силу монотонности / *(у) для векторов планов у^- G G_i,j и ^,y_i+₁,k G G_i+i,k из у і, >  уі+і,к следует, что /* ( у і,, ) > / *(5i₊i,k ) Для любого к = 1,j. По определению верхней оценки, g(Gi,j ) = / *( у і, ) и g(Gi+i,k ) = / Чуі+ik )• Поэтому из уі+^k 6 у і, следует, что g(Gi+i,k ) 6 g(Gi,j ) для любых подмножеств Gi+i,k С Gyj, к = 1,у, то есть верхняя оценка не возрастает по мере разбиения на подмножества.

Теорема доказана.

Особенности подхода

• 1.    Приведем особенности применения ММВГ для решения данной задачи оптимизации:

• •    разбиение каждого подмножества Gi,j на подмножества происходит не только с учетом параметров сетки и неубывания векторов планов, но и с учетом ограничений на планы L^t) — L5(t);

• •    дерево ММВГ хранится в виде списка, из которого исключаются отбракованные и/или раскрытые вершины;

• •    в качестве первоначального рекордного решения у берется ограничение Lⁱ(t);

• •    для дальнейшего ветвления выбирается подмножество решений с максимальной оценкой среди всех новых подмножеств разбиения;

• •    отсев некоторого подмножества Gi,j производится при выполнении условия g(Gi,j ) < /(у)-Д что при R >  0 позволяет не отсеивать решения, близкие к оптимальному;

• •    работа алгоритма ММВГ оканчивается, когда остается набор одноэлементных подмножеств разбиения, которые нельзя ни отбраковать, ни разбить на подмножества.

• 2.    Предложенный для решения оптимизационных задач для группы газовых месторождений подход объединяет использование имитационного моделирования, сеточных методов, дискретной и многокритериальной оптимизации. Основные этапы подхода:

• •    выделяется множество критериев оценки решений и среди них - один определяющий критерий;

• •    исходная задача дискретизируется за счет введения равномерной сетки для поиска приближенного оптимального решения;

• •    при помощи специального генератора строятся все допустимые решения;

• •    ищется приближенное оптимальное решение по определяющему критерию и множество близких к нему решений;

• •    на множестве полученных близких решений с применением методов многокритериальной оптимизации ищется реальное решение, наилучшее по многим критериям оценки.

• 3.    Для каждого варианта решений из множества близких работает имитационная модель группы месторождений, чтобы на основании выходных показателей модели рассчитать (как суммы по годам и по месторождениям) агрегированные показатели — критерии оценки данного варианта.

Данный подход совмещает достоинства традиционной и многокритериальной оптимизации, нивелируя их недостатки. Так, при традиционной оптимизации не для всякой задачи можно найти точное оптимальное решение либо нахождение такого решения требует слишком больших вычислительных ресурсов. Далее, не учитывается многокритериальность реальных задач, причем нахождение точного оптимального решения по определяющему критерию не всегда оправдано: такие решения обычно неудовлетворительны по остальным критериям и наверняка будут отброшены в процессе многокритериальной оптимизации.

С другой стороны, при многокритериальной оптимизации многокритериальные альтернативы обычно формируются в имитационном режиме, и ничего неизвестно о степени их близости к оптимальному решению по определяющему критерию.

Средства многокритериальной оптимизации позволяют найти реальный (рациональный) [1] вариант стратегии развития группы месторождений как наилучший по заданным критериям, таким как объем накопленной добычи газа, величина и длина «полки», капиталовложения, чистая прибыль, цена на газ, NPV и т.д. Анализ и выбор вариантов производится при помощи стандартных методов, таких как нахождение множества Парето, линейная свертка значений критериев, поиск вариантов в окрестности идеальной точки и т. д. Сохраняется последовательность вложенных друг в друга множеств отобранных вариантов, поэтому всегда можно произвести откат к предыдущему уровню процесса и изменить его направление и/или параметры.

Окончательный вариант стратегии разработки группы месторождений выбирается ЛПР по неформализованным критериям оценки на основании визуального анализа результатов многокритериальной оптимизации в виде профилей. Каждому варианту соответствует ломаная, соединяющая значения различных критериев, причем критерии отображаются по оси ОХ, а их значения — по оси ОҮ (см. рис. 4). После выбора ЛПР окончательного варианта стратегии для реализации вновь работает имитационная модель, формирующая полный комплекс показателей для данного варианта.

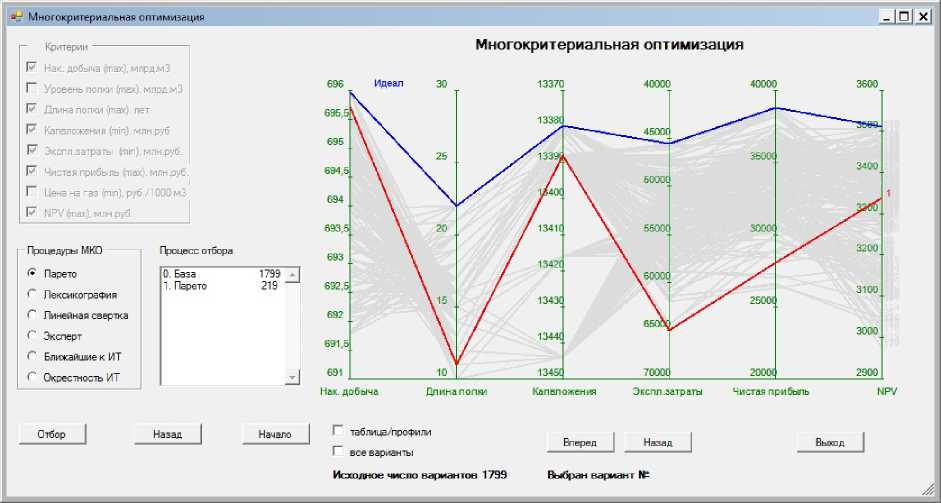
Рис. 4. Выбор стратегии для реализации с использованием профилей

Программная реализация

Рассмотренные выше методы и алгоритмы были реализованы в Системе моделирования и оптимизации добычи газа [3, 4], предназначенной для формирования наилучших стратегий разработки группы газовых месторождений газодобывающего общества или региона. Система была реализована в виде комплекса программ на языке C# в инструментальной среде Microsoft Visual Studio для Windows 7.0.

Система позволяет решать следующие основные задачи:

• •    распределение в имитационном режиме добычи газа в динамике между месторождениями при заданных планах добычи;

• •    расчет многочисленных технико-экономических показателей добычи в динамике по месторождениям;

• •    формирование плана добычи по группе месторождений, оптимального по критерию накопленной добычи;

• •    обеспечение многовариантных расчетов и выбор реального плана для внедрения, наилучшего по нескольким заданным критериям оценки, с использованием методов многокритериальной оптимизации.

Использование системы наиболее целесообразно в следующих случаях: достаточно большое количество месторождений в группе; долго- или среднесрочный период планирования; новые, еще не разрабатываемые месторождения; минимальная и/или прогнозная информация о месторождениях; планирование по укрупненным показателям для принятия стратегических управленческих решений. В частности, этим условиям удовлетворяют месторождения севера Тюменской области, Восточной Сибири, Дальнего Востока и арктического шельфа.

Комплексная отладка и опытная эксплуатация системы производилась на модельном примере группы месторождений Восточной Сибири; размерность решаемой задачи — 13 месторождений и 45 лет планового периода.

Важным выводом, полученным в ходе вычислительных экспериментов, является то, что «хорошие» варианты решений (близкие к оптимальному) образуются не только для планов с крутым выходом на УПД по группе и/или с большим значением УПД, но и для менее «напряженных» планов, для которых следует ожидать более хороших значений критериев экономического характера. То есть решения, близкие к оптимальному, находятся практически по всей области, покрываемой сеткой, что является следствием нелинейности системы.

Приведем наиболее общую последовательность действий пользователя при работе с системой.

• 1.    Ввести и сохранить параметры и исходные данные задачи планирования.

• 2.    Войти в блок оптимизации накопленной добычи, ввести параметры сетки и ограничения на планы добычи по группе месторождений.

• 3.    Проверить правильность ввода и проанализировать ограничения на планы в графическом виде.

• 4.    Решить задачу оптимизации накопленной добычи, получив множество решений, близких к оптимальному приближенному.

• 5.    Проанализировать результаты оптимизации, при необходимости изменить параметры задачи, ограничения и повторить процесс решение задачи (переход к п. 4).

• 6.    Сохранив результаты работы, войти в блок многовариантных расчетов.

• 7.    Для каждого из вариантов решений (полученных планов добычи) с помощью имитационной модели рассчитать динамику объемов добычи и технико-экономических показателей добычи и на их основе рассчитать и сохранить значения критериев оценки каждого из вариантов решений.

• 8.    Войти в блок многокритериальной оптимизации, определить множество критериев оценки вариантов решений и ограничения.

• 9.    Используя набор процедур многокритериальной оптимизации, технологию поиска с возвратами на дереве подмножеств отобранных вариантов, табличные и графические (профили) средства анализа множества вариантов, отобрать множество вариантов решений.

• 10.    Выбрать на этом множестве окончательный вариант решения на основании неформализованных критериев оценки.

• 11.    Для выбранного варианта с помощью имитационной модели рассчитать динамику объемов добычи и технико-экономических показателей добычи.

• 12.    Проанализировать результаты расчетов в виде таблиц и графиков.

Заключение

При дальнейшем развитии данной проблематики предполагаются учет ликвидации месторождений группы и учет неопределенности исходных данных (в первую очередь запасов газа различных категорий), что усложняет имитационную модель группы месторождений и увеличивает время решения оптимизационных задач. Также предполагается использование результатов моделирования и оптимизации как количественной базы для решения задач стратегического управления газодобывающим предприятием.