Решение оптимизационных задач в системах с секционными центробежными насосами

Исследованию характеристик центробежных насосов посвящено большое количество статей [1-4]. Так в [1] описана платформа с открытым исходным кодом для решения сложных задач оптимизации, которая предоставляет множество возможностей, включая эволюционные алгоритмы, алгоритмы роевого интеллекта, алгоритмы многоцелевой оптимизации, алгоритмы оптимизации с поддержкой.

Благодаря независимости от конкретной задачи, алгоритмы универсальны для работы в разных областях с различными уровнями, таких как мультимодальные ландшафты, дискретные пространства поиска, множество целей. С тех пор как платформа начала работать в 2017 году, она использовалась многими исследователями. Однако основные термины и концепции оптимизации вызывают трудности при освоении.

В статье [2] представлен и описан новый программный инструмент для анализа и решения задач оптимизации. Этот инструмент позволяет строить графики нескольких функций одновременно, перемещаться по ним и находить критические точки с помощью нескольких численных методов. В зависимости от разрешаемых проблем, пользователь может выбрать контекст в двух или трех измерениях, а также выбрать более удобный метод решения. Более того, изменение параметров в конкретном методе является прозрачным и понятным; цель этого программного обеспечения - упростить работу студентов, инженеров и исследователей, работающих в графической и интерактивной среде, с полностью интуитивно понятным пользовательским интерфейсом.

Представления играют существенную роль в математическом мышлении [3]. Они способствуют пониманию математических концепций и стимулируют развитие гибкого и разностороннего мышления при решении задач. Особенно это важно при использовании в задачах оптимизации - типе задач, который считается важным при преподавании математики и обучении в высших учебных заведениях. Результаты показывают тесную связь между успехами студентов в решении задач оптимизации и их умением использовать представления.

Нестабильные или плоские кривые напора могут вызвать проблемы при параллельных операциях или в плоских системах [4]. Несмотря на значительные усилия, которые были приложены для изучения нестабильности кривой напора в одноступенчатых центробежных насосах со спиральным корпусом, причина такого явления изучена недостаточно. В исследовании [4] рассматривалось изменение гидравлических потерь на основе взаимосвязи между распределением скоростей и полями генерации энтропии. Стационарное и нестационарное моделирование было применено для насоса с выходным диаметром рабочего колеса 174 мм, и нестационарные результаты в большей степени совпадают с экспериментами. Результаты показали, что потери в основном сосредоточены на всасывающей поверхности лопасти. Скорость образования энтропии в корпусе насоса при частичном расходе незначительно изменялась с уменьшением расхода, в то время как потери энергии в рабочем колесе резко увеличивались при снижении расхода до значений, равных половине расчетного расхода. Потери в рабочем колесе были в основном сосредоточены в области вблизи входа и выхода в рабочее колесо, где вблизи задней кромки лопасти возник вихрь, вращающийся в противоположную сторону. Вихрь вызвал резкое увеличение скорости образования энтропии на поверхности давления и в проточном канале. Такое увеличение было основной причиной нестабильности характеристик напора.

Исходные данные и методика расчета

В подавляющем большинстве названных и других статей были исследованы технические характеристики.

В [5] было показано, что в задаче оптимизации диаметра трубопровода системы водоснабжения необходимо учитывать не только нагрузочные характеристики, но и затраты на центробежный насос. Эта задача решается путем отыскания значения внутреннего диаметра трубопровода δ, при котором функция суммарных затрат на систему водоснабжения (капитальных и эксплуатационных) имеет минимум. Для чего производную от функции суммарных затрат по δ приравнивают к нулю. При этом возникает необходимость найти производную от стоимости центробежного насоса P по напору H .

В данной статье в качестве исходных данных был использован прайс-лист компании «Электромонтаж» на секционные центробежные насосы ЦНС производства «Пинский опытно-механический завод» (на 01.09.2023) [6].

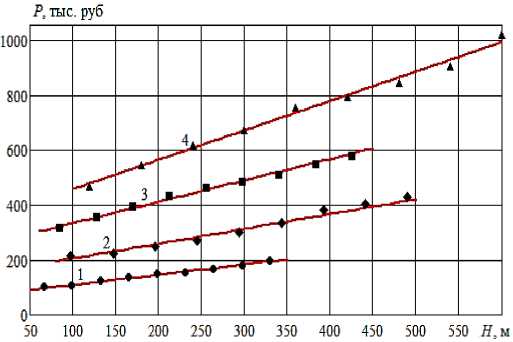
Было установлено, что зависимость стоимости ЦНС от номинального напора линейная (рис. 1):

P = P о + K • H , (1)

В табл. 1 представлены результаты определения значений P о и K •при разной величине номинальной подачи Q методом наименьших квадратов Рассчитан скорректированный (исправленный) индекс детерминации линейной модели R 1 ², который содержит поправку на число степеней свободы:

R i ² = 1 - (1 - R²)-(n - 1)/( n - 1 - m ), (2)

где R ² - индекс детерминации, рассчитанный без учета поправки;

n - количество значений для ЦНС с заданной подачей ( n = 9);

m - число степеней свободы, в линейной модели m = 2.

Н.Л. Великанов, В.А. Наумов, С.И. Корягин

рядка:

Рисунок 1 – Зависимость стоимости ЦНС от номинального напора при различных значениях подачи: 1 – Q =60 м³/час; 2 – Q =105 м³/час; 3 – Q =180 м³/час; 4 – Q =300 м³/час. Точки – данные [6], линии – результаты расчета по формуле (1)

Таблица 1 – Технические и стоимостные показатели центробежных насосов ЦНС

Q , м3/час	P 0 , тыс. руб.	K , тыс. руб./м	R 1 2
60	76,38	0,353	0,991
105	139,94	0,584	0,975
180	262,42	0,752	0,993
300	348,34	1,077	0,983

По табл. 1 видно, что индексы детерминации весьма высоки. Значит, линейная модель пригодна для расчетов.

Результаты и их обсуждение

Найденные значения K и представляют собой величины производной от стоимости насоса по напору. Таких значений достаточно при решении задачи оптимизации диаметра водопровода при заданной (фиксированной) подаче, что характерно для проектирования централизованных систем водоснабжения городских районов и поселков. Обобщенные характеристики канализационных насосов высокой производительности рассмотрены в работе [7]

Однако в промышленных системах водоснабжения нередкими бывают условия, когда задан объем воды (или иной жидкости), который необходимо перекачать. Тогда Q становится еще одной независимой переменной (аргументом). При решении такой задачи требуется найти зависимость стоимости насоса от двух аргументов: P ≡ f ( H , Q ).

По табл. 1 P 0 и K являются возрастающими функциями подачи насоса Q :

P 0 = f 1 ( Q ), K = f 2 ( Q ). (3)

По рис. 2 видно, что зависимости (3) отличаются от линейных. Было установлено, что их можно аппроксимировать многочленами 2-го по- f1(Q) = a0 + a1Q + a2Q2, f2(Q) = b0 + b1Q + b2Q2. (4)

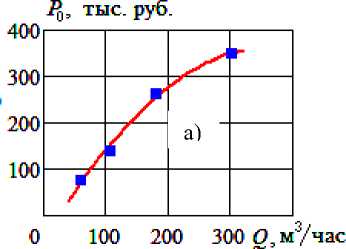
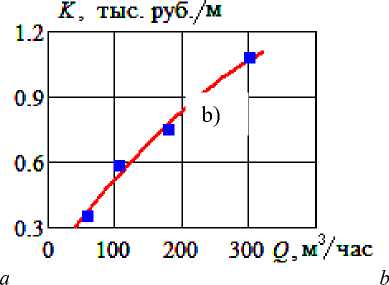
Рисунок 2 – Зависимость величин P 0 ( a ) и K ( b ) от номинальной подачи насоса. Точки – по данным [6], линии – результаты расчета по формуле (3)

По рис. 2 видно, что результаты расчета по формулам (3) хорошо согласуются с данными [6]. Значения коэффициентов в формулах (4) были получены методом наименьших квадратов, для ЦНС:

a 0 = –55,78; a 1 = 2,30; a 2 = –0,00316; b 0 = 0,132; b 1 = 0,00428; b 2 = –3,846·10^–6 .

Теперь можем записать зависимость стоимости насоса ЦНС от двух аргументов:

P ≡ f ( H , Q ) = ( a 0 + a 1 Q + a 2 Q ²) + ( b 0 + b 1 Q + b 2 Q ²)· H .                         (5)

Найдем исправленный индекс детерминации модели (5). Теперь в формуле (2) общее число точек n = 36; по количеству необходимых параметров m = 6. Расчет по (2) дает значение R 1 ² = 0,989, которое говорит о высокой адекватности модели (5) данным [6].

На рис. 3 представлен контурный график.

Заключение

Проведенные исследования для секционных центробежных  насосов показали наличие нелинейных    зависимостей    стоимостных характеристик от параметров насосов. Эти обстоятельства  необходимо учитывать при проектировании и модернизации гидравлических сетей и насосных установок.

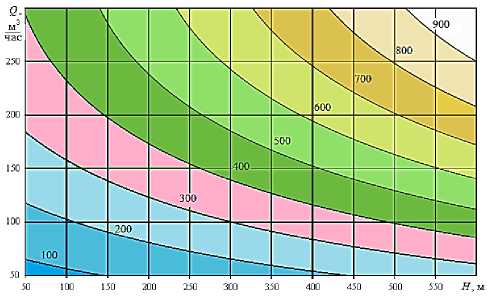
Рисунок 3 – Контурный график зависимости стоимости ЦНС (тыс. руб.) от номинального напора и подачи