Решение осесимметричной задачи теории упругости для несжимаемых материалов с помощью гибридного метода конечных элементов

П = ff- «IS1° * ^[LJu ) dV , v

где [L] -дифференциально-алгебраическая матрица, задающая гео метрические соотношения: е = fLj u , q fSJ - матрица в законе Гука в ~ fgj а.

Для осесимметричной задачи интегрирование по объему можно заменить интегрированием по площади:

П =              [Slo + о^Т[L]u ) ДА                 (3)

R J 2                   q е

Ае

(используем обычную цилиндрическую систему координат). Тогда векторы и матрицы в П^ имеют следующий вид:

о =                 ; ^е = I^е ; u = £и ш J^T ;

R Z RZ У               R Z RZ У         q q q

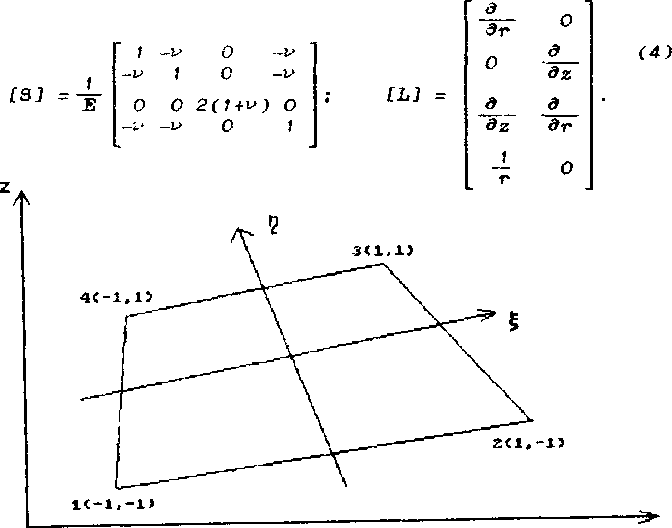
Рис. 1. Конечный элемент.

Для четырех угольных изопараметрических элементов рис.1 согласованное поле перемещений и будем аппроксимировать билиней- ными базисными Функииями:

и q w q

"sohokoso

12  3  4

OS О ОО W

L 123.

q q

< m- u - вектор узловых перемещений; ГК ] - матрица согласован-q                                                q них базис ных Функций, ее компаненты имеют вид:

№ = L (1 _{^ ^ )(1^.п) . I 4        i          i

<

омер узла. Выберем

гласно

[ЭР для напряжений ап-

цдаксиманию, независимую

О'

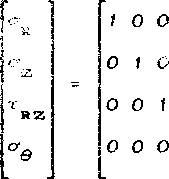
О

о

о

{3

п

о

о

О

о

о

о

о

о

о

о

о

Г)

о

о

о

о

о

о

о

о

к

т>

^3

о.

+ [Ф№ъ

т)

о

о

о

о

^1Z

где р

т

(f3 (3 р .(3   ] .

*5 <5 7        12

В этом

выражении (5

вектор внутренних параметров

напряжений

задающих постоянную аппроксимацию на элементе, /3^

вектор па-

раметров, задающих линейную аппроксимацию. Таким образом, поле напряжений внутри одного элемента является полным полиномом полиномом первого порядка, следовательно, поле перемещений должно быть полным полиномом второго порядка. Для этого введем дополнительное несогласованное поле перемещений ti в виде:

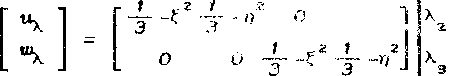
№Х]Х .

где X - вектор внутренних параметров перемещений; £19^ J “ матрица несогласованных базисных Функций.

Очевидно, что на границе элемента полное перемещений u=ix "4t^ совпадает с согласованным полем лишь в нескольких точках. Поэтому в общем случае поле перемещении на границе двух соседних элементов оказывается разрывным, и Функционал Рейсснера для одного элемента следует дополнить еще одним слагаемым:

0_r = 2nJr(- — c^T £S.?o-+o^T fLRu^+u^ JM4_e-2rrfr7^    ,    (9)

А                               Г где Г - граница элемента; Т - усилия, действующие на границе е со стороны соседних элементов.

Вновь введенное слагаемое имеет простой Физический смысл, поскольку il^ ~ не что иное, как невязка в перемещениях, а поле перемещений должно удовлетворять условию непрерывности на границе между смежными элементами, то для выполнения этого условия невязку в перемещениях необходимо ввести в Функционал с множетелями Лагранжа, роль которых выполняют Т. Выразим Т через вектор напряжений:

7 = с^Т £п/  .                                     (10)

где [п] ~ матрица направляющих косинусов нормали участка границы dT к осям ОН и 0Z- Матрица (и) имеет вид:

п °

£п/

О ⁿz

П^ ПГ о о

Представим вектор сх в виде суммы постоянной и линейной компонент:

a = »с+ а^                                            (12)

где а,- р^, а ^ [Ф] (3^. Тогда

П^ = 2njr(--^- »^т[ЗЗ" + с^т[L]u,_q + с7 [ЪЗи^) ал_в-

- зп^то^Еп]¹^ аг_е Г_е

- Snjrc^tnj¹^ dT, Г_е

Последнее слагаемое в (13) преобразуем по Формуле Грина:

^J^fnJ^1-^ дГ_е= JrffLJ^/t^ dA_e + Jro^fXjt^ дд^ , ₍₁₄₎

где д dz

EL]

Непосредственным интегрированием нетрудно убедиться, что

Jr([L]o-c)'IuK dA, = О

Следовательно, интеграл по границе преобразуется в один интеграл по площади,а если заметить, что в (13) третье слагаемое может быть разложено в сумму:

°ctL3ux = °Tc[L3ux * ^^^

то два одинаковых интеграла с разными знаками уничтожатсяи мы получим:

Heo" - '‘^лым условием с л e д укг ₍е о ус лови©:

Гто-^п]1^ dT

Данному условию вующего выбора ;

выражени е апп рокоимэ1

t t ov£b)tu ) АЛ - q h A. e

стационарности Функционала является

Jt4^ fn J^ dr

С

'. удовлетворять

а$аЦИИ для

и

ar-p.

A.         z 11     eh

h

h

О

априори за счет соответст-

Подставляя в

получим

полученное

или

«г: ®.t 3 •=J rtoxf [пНФ-фзаг

Поскольку

оощем

случае Х^О, то [М]р =0- Тогда

р и j

О

ft (ft ft ft ft f i 5 s 7 a

преобразуя последнее

-№ Р Р Р ) ■ о ю и 12 выражение, получим

1^

(21 )

ли только det [#„3*0- Тогда, обозначив о вектор напряжений

если он аппроксимируется не двенадцатью.

а

восемью

параметрами напряжений /3

получим

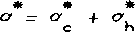
^^[Ф^ЗР^ЕГ.Ф*]

*  *

=[ф № где [I] - единичная

матрица; [ф*]=[ф_т]-[ф_н][м_и] Чм,]-

С учетом замены о на о Функционал Рейсснера примет вид:

_      1           A Ат         АТ nR = 2п^т(- -g-o [3)а *О [Du^+o^ [Di^) Д4е.   (23)

Ае

Настоящую Формулировку можно интерпретировать следующим образом: если введение несогласованных перемещений и^ рассматривать ^ак способ получения наилучшей аппроксимации для напряжений о на элементе, то тогда можно сказать, что может быть использовано вместе с только лишь согласованными перемещениями и -В таком случае имеем следующий Функционал: q

H_R “ 2nJ^rt- ^^ ^Тi^a^° *° ^Tfbju_q) dA^ .            (24)

А

(Заметим, что удаленное слагаемое должно иметь более высокий порядок малости по сравнению с другими слагаемыми и тождественно равняться нулю без принятия каких-либо допущений в случае,если конечный элемент представляет собой параллелограм, пара сторон которого параллельна оси OR. Для элемента, произвольно ориентированного по отношению к глобальным осям координат, этот Факт равенства указанного слагаемого нулю подтвердить или опровергнуть не удалось ввиду исключительной сложности аналитических выкладок).

Условия устойчивости Бабушки-Бреззи для элемента, основанного на О' и и , будут следующими: q йЛт(о ) > dimfu )-т ,                                (25)

q где г ~ число степеней свободы элемента как твердого целого, а dimO - размерность величины (), т.е. число параметров этой величины. В случае осевой симметрии г=1> d.im(or )  =  8 и dimfu )=8> т.е. введенный элемент удовлетворяет условию устой-q чивости.

Для задачи определения осесимметричного напряженно- деформированного состояния некоторого тела Функционал энергии запишется так:

п Л . - V .                                             (26)

где суммирование производится по всем конечным элементам, а У обозначает потенциал внешней нагрузки:

У = 2^ Г гр^Ти ДГ .                                    (27)

^J q р Г р Здесь Г часть границы, на которой заданы силовые граничные р условия (кинематические граничные условия будут добавлены в качестве дополнительных). Вектор p^T=fp_rP_z¹ “ ^это распределенная (на единицу боковой поверхности) осесимметричная нагрузка.

Условие стационарности Функционала П имеет вид:

6П - О ,                                                  (28)

* где варьирование следует провести отдельно по (3 и и .

ч

Преобразуем выражение (24) , подставив в него аппроксимации для и и - Тогда: ч nR        [КЗП + ^ [с№ .                      (29)

где [КЗ = 2п^г[Ф* З^т [S3 £Ф* 3 OA_q ;

[сЗ = 2п^т[Ф*3Т[L3[Hq3 dAe . Ае

В локальных координатах ,т)> матрицы [НЗ и [о] примут вид: 11

[h] = 2пД гГФ* J^T [33£Ф* J|detj| dtdn ;

(сЗ = 2пД т[Ф*3^Т[L3[N_q3\detj\ d^dtn . -1-1

Здесь: г = a ta [ta ii+a^D ;    | detJ\ =d₂+d_g? +4^ .     (31)

где d =CL Ъ —CL Ь 2 3  12  2 1

d =а Ъ -а Ъ ; Д=а Ь -а Ъ ; 1   2 3   3 2      2   1 3   3 1

1 а1 Ь1 -1 1 1 -1 Г 2 1 1 а2 ь 2 1 -1 1 -1 Г 2 2 2 % Ьз -1 -1 1 1 Г 2 3 3 а4 ь4 1 1 1 1 r*4Z< - каждая пара <г.,х.) дает координаты соответствующей вершины : ламента в глобальной системе координат. Матрица £Ф*3_£1".Ф^З состоит из двух подматриц, каждая размером 4x4- £13 - единичная подматрица, а [Ф^З имеет вид:

Этесь т. ~ этс элемент матрицы

£М З^-1 £11 3> где матрица

	17-т11?      ’’Л/     П-“11?     П-”11^ -m 17                   . 17                   . 17                   , 17
f®*J =	-^Sl^-™»!17 -^з/"^!17 Л^Л^ ^"з/-”*!17 0           0           0           0

■оставлена в таьляце 1, а элементы [Ы^] таковы:

Таблица 1

8 .        16 , —-- b a - -т d 3 з 4  45 з 88 — —b а 45  2 1	0	8 88 *-45aia2	16 —а а 9  2 3
8 .        8 , ™ bta2+-gb2a	0	16 --тг- а а 9 12	8 —т а. а. — 3 14 88 - 45 агаз
0	56 9  2 3	8к      ?б ' ^bS%-"45 Дз 88 . 45 Ь2а1	- b а -9   3 2 8 . 9  2 3
	8 " Т “I “4 ‘ 88 -745 “-2%	f-b^A -fb2ai	8 .        16 , -ybia«-^5di 88 . 45 г з

*     s ,      s г        i   s ,      se „       >6.

11   9  3 2  9  2 3   21  314  45  23  45

iS     88       i   16(33)

32  з  з 4  45  1 2    42     9

(остальные равны нулю). Введем обозначение [В]= г [L] [Я ]- ч Матрица [В] имееч* размерность 4x8, при этом

^ ^ ^tJ ^{[ ( b}3 - \ ^ <^b3 "^b2 ^⁺ ^2 ~\ ^ ³

^bi7~ ^b33-^£tJ ^^^-^з^^^-АЛ^'

^b31^{= b}22- "^tj ^{[ (}% '“1 ^A ⁺% ^{)7)+ (a}i ^+a2 ^{)? 3 ;}

r                                         (34)

^b33= ^b24= 4ctetJ       ^+a3 ^{)+ fa}3 -^a2 ^?7>-^fai ^+a2   ^{3 :}

Ь_а - Ь, _1d^_tj " ^[(ai ~^a3 ^)+(a2 ~^a3 ^№ltol ^-a2 ^ ^{3 1}

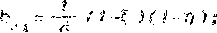
Ь^ -~ (t^)(t^)

а остальные элементы матрицы [В] равны нулю.

Интегрирование при вычислении матрицы [с] и [h.] целееооб{ зно провести по квадратурной Формуле Гаусса [1]:

113 3

П?^^> ^^ =2 2^Л fav1T,1) '

-1-1

где ^^q^-V 3/5 ; F^^ 0 ;   ^э'^з^ У 3/5 ’ к =к =5/9 ;        к =8/9 .

После варьирования Функционала П отдельно по и и Р нот," чим систему линейных алгеброических уравнений СС.ПАУ) следующего вида:

[И] [С]

[cf О

Г ъ Г о 1 и Ч И

Рассмотрим каждую компоненту СЛАУ в отдельности. [Н] прйд- с тэвляет собой блочно-диагональную матрицу размерностью (8®КЙ)*(8*53) Элементов, где 53 ~ общее число конечных элементов. Она имеет вид:

О

[Н]

(37 )

h NSl

Матрица [с]Т может быть представлена в виде:

[cf=[cT:cT:.. „ :с Ъ ,                              ов)

где fc j^5, получается из Го J^T следующим образом. Если в где-

•бальной нумерации узлов конечно-элементной модели лока.пьнъ?е номера узлов 1,2,3,4 (для конечного элемента с номером i) равны соответственно k,i,m,n, то первая и вторая строки [с ]Т переносятся в строки 2к-1 и 2k матрицы [С.]т, третья и четвертая - в строки 21-1 и 21 и т.д. Таким образом, в [С. JT из 2 * RR

(где RR - общее число узлов в модели) лишь восемь отличны от нулевых; остальные строки - нулевые. Вектор Ь имеет вид:

т *т *т*т

1 ' 2 ‘      " NS '

*т *   **

Вектор и выглядит так:

U=[U ,w .о .w .....и .w f. ql ql q2 q2       qNR qNR

Вычисление вектора У индентично обычному методу конечных элементов в Форме метода перемещений [ 1 ]. Отметим, что СЛАУ <37^ может быть очень плохо обусловлена из-за того, что элементы матриц [И] и [0] имеют разный порядок. Поэтому перед решением системы <37> следует применить масштабирование.

Представленная версия ГМКЭ реализована в виде прикладной программы для ЭВМ IBM PC/AT (транслятор Турбо-Си 2.0). В качестве тестового примера рассмотрим задачу анализа НДС шарового подпятника (рис.2) (решение этой задачи, представленное в [2], является ошибочным). В сферической системе координат уравнения в перемещениях и условие несжимаемости выглядит так £2]:

• 1 д               ~           1 д                 --,

• —---(sin р )  --[sin р ^Ш_^Т) I*

• г sin Р др              г sin р др         д т

д² и д² (г w) dS

• —-- + ----— + -- = О ;

д т др        д т*        др

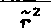
д(г2 П)

д

1 d(w sin р)

---= О .

т sin р др где и - переменная вдоль координаты г ; иг переменная вдоль угловой координаты ^- ; в ~ гидростатическое давление.

Рис. 2. Расчетная схема.

Кинематические граничные условия имеют вид:

u(R )=0 ; u(R )=-Д соз¥> ;

(42) w(R_z)=O ; w(R_i )- A sinp .

Аналитическое решение задачи таково:

• △ д(г /(г))

и.= -Д/(г) cosp ; ш=--- ----------- sin ч> :

2г 5 г о~=оД(6С2г+ЗСаг 2+бС^г *) cosip ;

a^zr9=G&( 12С₂т-ЗС^г *) coav ;                       (43)

т- - ОД(30 г+ЗС г *) simp ; г              2       4

5=Д( ЮС^г+С^г 2 ) co8f> .

где G ~ модуль сдвига материала;

С1 = (5-9а2+4а 3)D~4 ;         Сг=3(о?-1^«'2D 1 ;

3-2-1             Э - 3   -1

С =6Д fa -а )В ;          С =2R (<^  -1 )D ;

а=Я₂/Я₁;   D=10-9(a"² +<х³ )+4(а³ -а"³ ) ;

f(T)=G1*C1lT3*C3r-t*C^3 .

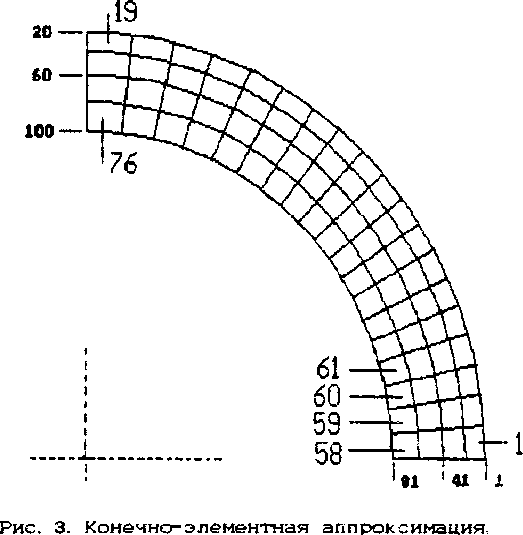
В качестве примера рассмотрим задачу со следующими исходными данными: G= 1 МПа, v— О.5, А= 1 мм, R —1 ОО мм, R =80 мм. Конечно-элементная модель Срис.З) содержит 100 узлов и 76 элементов. Результаты таковы: максимальное вертикальное перемещение имеет узел 4V, при этом аналитические Формулы дают w=3.89 мм, а численное решение tv-3.92 мм. Напряжения вычислялись в центрах конечных элементов, при этом интенсивность напряжений напряжений достигает максимума в элементах- 58. 59. 60. 61 (табл.2).Как можно видеть, погрешность численного решения не превышает 8% .

Таблица 2

Элемент	а. аналитическое, МПа	о численное, МПа
58	0.988	0.999
59	0.981	1.06
60	0.968	1.02
61	0.948	1.01