Решение позиционных и метрических задач начертательной геометрии

Ключеве слова : простой, частного алгоритма, окружность, поверхностей вращения, линейчатых поверхностей, плоскость, позиционных.

Деление задач на позиционные и метрические является условным. Из всего многообразия задач позиционную группу можно выделить, то чисто метрические задачи встречаются очень редко. Эти задачи можно отнести всего лишь к одному из двух групп: 1-я группа – задачи позиционные; 2-я группа – задачи метрические.

Несмотря на это, распределение задач по отмеченным группам в методическом отношении имеет большой смысл, так как позволяет установить единые (обобщенные) алгоритмы, пригодные для решения широкого круга задач, входящих в одну группу, и как следствие, обеспечить простой и надежный поиск частного алгоритма для решения поставленной задачи.

Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или (линии) или же множеству (поверхности). К позиционным относятся также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам.

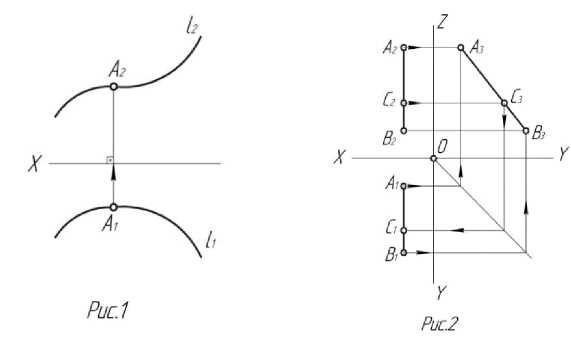
Пример 1. В плоскости Σ(m ∥ n) указать произвольную точку А (рис.1)

В качестве линии, как правило, выбирается образующая поверхности. Если поверхность может быть получена образующей различной формы, то предпочтение следует отдавать наиболее простым и удобным для построения линиям: окружностям для поверхностей вращения, прямым для линейчатых поверхностей (в частности, для плоскости целесообразно использовать линии уровня).

Решение. В плоскости Σ проводим произвольную горизонталь h. При построении ее проекций следует иметь в виду, что прямая принадлежит плоскости в том случае, если она содержит две различные точки, принадлежащие плоскости. В качестве таких точек принимаем точки 1 и 2, принадлежащие соответственно прямым m и n, определяющим плоскость Σ.

На рисунке рис.3. построение проекций горизонтали h выполнено в следующей последовательности:

на прямой m взяли произвольную точку 1,через

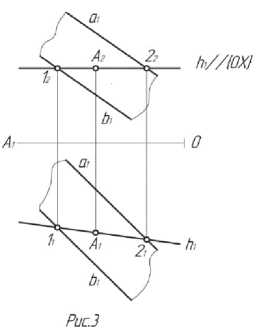
фронтальную проекцию этой точки провели фронтальную проекцию горизонтали h2;отметим точку 22=^2 А Ь2;определили горизонтальные проекции 11 и 21 точек

1 и 2;

через точки 1 1 и 2 1 провели горизонтальную проекцию горизонтали h 1 .

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых линейными и угловыми величинами.

Все многообразие метрических задач в конечном счете сводится к двум видам:

А-задачам на определение расстояния между двумя точками;

Б-задачам на нахождение величины угла между двумя пересекающимися прямыми.

К метрическим относятся такие задачи, на пример – построение отрезка и угла с наперед заданным значением соответственно линейной и градусной (радианной) величины.

Несмотря на то, что чисто метрические задачи встречаются редко, целесообразно выделить их в самостоятельную группу, включив в нее и те задачи, в которых на промежуточных этапах решения приходится выяснять позиционные отношения между геометрическими фигурами.

Рассмотрим возможные пути решения на определение метрических характеристик геометрических фигур.

Определение расстояния между двумя точками. Графическое определение длины отрезка [АВ], является мерой расстояния между точками А и В, путем построения прямоугольного треугольника.

Пример 1. Определить расстояние между точками А и В (рис.2). Pешение задачи сводится к нахождению длины отрезка, концами которого являются точки А и В. Переводим отрезок [АВ] из общего положения в частное - параллельное плоскости П 3 , используя для этого замену плоскости П 2 плоскости П 3 .

Новую плоскость П 3 выбираем так, чтобы отрезок [АВ] оказался параллелен этой плоскости. Для этого новую ось Х 1 проводим параллельно [А 1 В 1 ]. Длина отрезка [А ^ В ^ ]-новой проекции отрезка [АВ]-укажет искомое расстояние.

Пример 2. На рис.3 приведено решение этой же задачи путем перемещения отрезка АВ параллельно плоскости П 1 в положение А 1 В 1 , параллельное горизонтальной плоскости проекции. В этом случае отрезок будет проецироваться на П 1 без искажения.

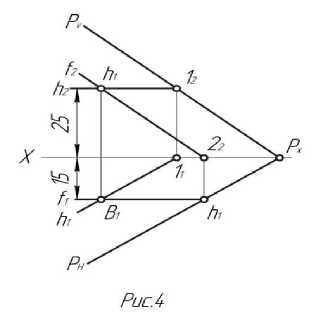
Пример 3. На рис. 4 для определения длины отрезка АВ его перевели в положение, параллельное плоскости П 1 , путем вращения вокруг оси i 1 П 2

ВЫВОДЫ:

Распределение задач по отмеченным группам в методическом отношении позволили установить обобщенные алгоритмы, пригодные для решения широкого круга задач, входящих в одну группу и обеспечено простой и надежный поиск частного алгоритма для решения задачи.

При определении расстояния между двумя точками использован правильно метод перевода отрезка из общего положения в частное, применив при этом один из способов преобразования ортогональных проекций, или замену плоскости проекции или плоскопараллельное перемещение.