Решение рациональных неравенств в задачах ЕГЭ

Неравенство - это два числа или математических выражения, соединенных одним из знаков: > (больше), < (меньше), ≥ (больше или равно), ≤ (меньше или равно).Неравенства, содержащие знак > или <, называют строгими, а содержащие знак > или <, - нестрогими [1].

Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Неравенства, имеющие одни и те же решения, называются равносильными.

Неравенство, левая и правая части которого есть рациональные выражения относительно x, называют рациональным неравенством х.

Например, являются рациональными неравенства

х — 1

х2 — 5х + 5    1

х + 1   > х + 5 + ^"

(х —1)(х + 3) > 0,   — <0,

При решении рациональных неравенств приходится умножать или делить обе части неравенства на неравное нулю число, переносить члены неравенства из одной части в другую, применять правила сложения и вычитания алгебраических дробей. В результате получается неравенство, равносильно предыдущему, т.е. неравенство, имеющее те же решения [2].

Рассмотрим рациональное неравенство

^) >0, В(х)

где Л(х) и 5(х) - многочлены относительно x .

Любое решение неравенства (1) есть решение неравенства

Л(х)^(х)>0,                    (2)

Если x 0 – решение неравенства (1), то справедливо числовое неравенство ^у^) > 0 , означающее, что числа Л(х₀) и В(х₀) имеют B(X q ⁾

одинаковый знак, то есть справедливом числовое неравенство Л(х₀) • 5(х₀) > 0. Из этого следует, что число х₀ - решение неравенства (2).

Если многочлены Л(х) и 5(х) разлагаются в произведение разных двучленов вида х — х0, то все решения неравенства (1) можно получить, решив методом интервалом неравенство (2). Учитывая это обстоятельство, часто не переходят от неравенства (1) к неравенству (2), а говорят о применении метода интервалов к неравенству (1).

Пример 1:

Решите неравенство

х2-6х+8

х-1

х-4 х2-3х+2

< 0 [3].

Решение:

• 1)    Необходимо разложить квадратные трехчлены, входящие в неравенство, на линейные множители:

х2 — 6х + 8 = (х — 4)(х — 2)

х2 — 3х + 2 = (х — 2)(х — 1)

Неравенство принимает вид:

(х-4)(х-2)      х-4      „

--7----77----Г <  о. х-1      (х-2)(х-1)

• 2)    После приведения дробей к общему знаменателю, вычитания дробей и вынесения общего множителя неравенство преобразовывается к

следующему виду:

(х-4)(х-2)2-(х-4) <

(х-2)(х-1)    <

(х-4)((х-2)2-1) <

(х-2)(х-1)   <

⁽ х-4)(х-1)(х-3) _<

(х-2)(х-1)   _

• 3)    В последнем выражении можно сократить дробь на многочлен x-

• 1,    при условии, что х ^ 1.

(х-4)(х-3) _< Q

(х-2)-

• 4)    Решая с помощью метода интервалом, приходим к ответу:

  -   +   -+

о----о----•----•>-

1     2    3    4х

Рис. 1. Решение примера 1.

Множество решений исходного неравенства: (—^; 1) и (1; 2) U [3;4].

Ответ: (—^; 1) U (1; 2) и [3; 4].

Пример 2:

Решите неравенство х³ + 2x 2

—

24х2-х+3

х-3              .

Решение:

• 1)    Необходимо перенести члены неравенства из одной части в

другую, применить правила сложения и вычитания алгебраических дробей:

х4+2х3-3х3-6х2-24х2+х-3-х+3 ^ q х-3             — х4-х3-30х2

х-3    —

• 2)    При вынесении общего множителя и последующем разложение

числителя на множители получаем неравенство:

х2(х+5)(х-6) < q х-3

• 3)    Решая с помощью метода интервалов, приходим к ответу:

  

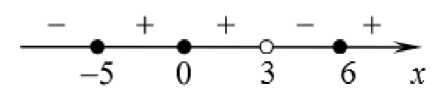
  Рис. 2. Решение примера 2.

  
  

Множество решений исходного неравенства: (—^; —5] и {0} и

(3; 6].

Ответ: (—^; —5] и {0} и (3; 6].

Пример 3:

Решите неравенство ^- + ^1^ <5 [3].

Решение:

• 1)    Необходимо перенести члены неравенства из одной части в

другую, применить правила сложения и вычитания алгебраических дробей:

5х2-15х+11 <  q

(х-1)(2-х) ^_   "

• 2)    При разложении числителя на линейные множители получаем следующее неравенство:

15-У5     15+У5\

У 10 Д^%  10 ) _< 0

(х-1)(2-х)     _'

• 3)    Применяем метод интервалов для неравенства: —     +      —     +—

  -----о-------•--------•------о*■

• ¹     15-V5 15 + V5 ^{2 х}

Рис. 3. Решение примера 3.

Таким образом, решить рациональные неравенстве, встречаемые в контрольно-измерительных материалах ЕГЭ по профильному уровню математики, можно с помощью тождественных преобразований, переходу к равносильному неравенству и дальнейшему применению метода интервалов.