Решение расширенного уравнения распространения импульсов в оптических волокнах для конкурирующей нелинейности

Поле оптического импульса, распространяющегося в одномодовом волоконном световоде, поддерживающем состояние линейной поляризации, имеет вид [1].

E ⁽ r , t ) = e x ^{F (} x , У ) ^{A (} z , t ) exp { i ( ^в o2 ^- to ot ) } ,        (1)

\                4,                    J^{- (} x 2 ⁺ y ²⁾ 1

где f ( x, y ) - гауссовская функция вида exp <----- 2--- ^

[ w с радиусом моды w, A(z, t) – комплексная огибающая импульса, too - несущая частота, в o = to on (too)/ c -центральное волновое число.

Для огибающей оптического импульса выведено

• [2]    уравнение

. ( d A „ d A ^ 1 d ² A в ₂ d ² A t d z ¹ d t J 2 в o d z ² 2 d t¹ +Ap (| A ²) A = 0,

названное расширенным уравнением распространения, которое существенно отличается от традиционного, называемого основным уравнением распространения [1], наличием второй производной по координате. Здесь в 1 = 1/ v g - величина, обратная групповой скорости, β 2 – дисперсия групповой скорости, Ap(| A |²) - нелинейная поправка к постоянной распространения моды в линейном приближении, которая выражается через нелинейную часть Δ n показателя преломления:

kot f^A n F ^{( x} , У ) d x d y

Ав =     -------й-------,

J] I F ⁽ x , y )| d x d y

где k o = to _o I c .

В области прозрачности волновода Δβ является вещественной функцией. Так как β2 в области прозрачности отрицательно, то тип уравнения (2) – эллиптический. Если в уравнении (2) отбросить одну из вторых производных, то полученное уравнение параболического типа сводится к нелинейному уравнению Шрёдингера, которое является на сегодняшний день самым изученным из нелинейных уравнений, допускающих солитонные решения. Сводку различных его решений можно посмотреть, например, здесь: ,

Полные уравнения второго порядка рассматривались и ранее. Так, в [3] выведено уравнение гиперболического типа для неограниченной керровской среды в упрощённой модели поля, не зависящего от поперечных координат, но затем это уравнение упрощается до нелинейного уравнения Шрёдингера. Следует упомянуть и статью [4], в которой методом секанса и tanh-методом решаются некоторые полные уравнения второго и даже третьего порядка, однако полученные решения сингулярны. Решения же в статьях [2], [5] являются гладкими локализованными функциями, как и в данной работе.

При небольших пиковых значениях интенсивности вводимого излучения нелинейную часть показателя преломления представляют степенным рядом

A n = n ₂ | E |² + n 4 | E |⁴ +••• , (4) что согласно (3) приводит к степенному разложению функции Δβ:

Ав = у| a| ² +ц| a| ⁴ +••• , (5) где параметры γ и µ зависят от характеристик световода. При достаточно малых интенсивностях оптического поля вторым слагаемым в (5) пренебрегают.

Полученная нелинейность называется керровской, и солитонное решение уравнения (2) для этого случая найдено в [5].

С ростом интенсивности вводимого излучения наблюдается [6] отклонение от керровской зависимости показателя преломления и необходимо учитывать второе слагаемое в формуле (5). Такая нелинейность называется конкурирующей (иногда этот термин применяют только в случае, если слагаемые в (5) различаются знаком).

Экспериментальные исследования в нелинейной оптике [6] подтверждают такую зависимость нелинейного показателя преломления от интенсивности оптического поля в полупроводниковых волноводах, стёклах, допированных полупроводниками, и органических полимерах.

Целью настоящей работы является нахождение локализованных решений уравнения (2) в элементарных функциях для конкурирующего нелинейного отклика среды на внешнее гармоническое возмущение.

Основной формализм

В [5], [7] показано, что если искать локализованное решение уравнения (2) в виде

A ( z , t ) = R ( z , t )exp { iqz } , (6) где R – действительная функция, а q – произвольный параметр, являющийся поправкой к центральному волновому числу в _o , то функция R определяется

пиковое значение напряжённости выражается следующим образом:

E max

двумя квадратурами:

I /    dR2      2 =^ ,(7)

^J R1 - - B ( R ²)/ pR²

R ²

B(R2) = J Ap(I)dI.(8)

Здесь

^ = I 2 p Po (z — z — vt),(9)

V1 -Po P2 vo’ p = q(1 + q /2po),(10)

v = vg (1 + q / в o),(11)

2 7 p / Y

1 + + 71 + 16 p Ц / 3 y ²

Отсюда находим

Y E^ Ц Е 4_ax max । max ^p 2      3

Теперь из формулы (10) выражаем

q = ^p o

^{- 1} ±

V

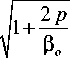
или, подставляя сюда (18), окончательно получим

q = ^p o

(

^{- 1} ±

V

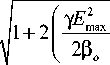
h e l ) з в o J

A

где z 0 – произвольная постоянная, определяющая начальное положение импульса.

Полагая в (8)

Ap = y I + Ц 1 ²

и подставляя полученное выражение в (7), имеем

J            d R            = ^ .

^J R 71 - ( Y R ²/2 p \u. R ⁴/3 P )

Интеграл в левой части (13) с помощью подстановки u =1/ R сводится к известному [8] интегралу, и в результате получим

1 . 1   1/R2-y/4 p.

— Arch .= ^

• ²      7y² /16 p 2 +Ц /3 p

Обращая это выражение, находим

2 J p / Y

R = ! I.

71 + 71 + 16 p ц /3 Y ² ch 2 ^

Формула (15) описывает вещественную огибающую волнового пакета, локализованного вдоль направления z = z o + vt и движущегося с постоянной скоростью (11).

C учётом (6), солитонное решение уравнения (2) имеет вид:

A ( z , t )

27 p / Y exp{ iqz }

1 + 71 + 16 p Ц /3 Y 2 ch 2 ^

В том, что (16) является решением уравнения (2), можно убедиться прямой подстановкой. Последняя формула представляет собой однопараметрическое семейство решений, в котором свободным параметром является q .

От свободного параметра q (а вместе с ним и от p ) удобно перейти к новому свободному параметру [9] амплитудного характера. Действительно, из соображений размерности и из формулы (15) следует, что

Формулы (16), (9), (11), (18), (20) решают поставленную задачу.

Заключение

Таким образом, в явной аналитической форме найдено солитонное решение уравнения (2) для конкурирующей нелинейности. Каждый солитон характеризуется своей амплитудой и постоянной скоростью, зависящей от амплитуды.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013–2020 годы.