Решение терминальной задачи управления для нелинейных динамических систем

Рассматривается один из методов решения задачи управления нелинейным динамическим объектом. Имеем объект, заданный нелинейным дифференциальным уравнением

-г = f ( x , u ).                  (1)

dt

Необходимо найти такую функцию управления u ( t ), что за конечное время T система (1) перейдет из начального состояния x (0) = x ⁰ в конечное x ( T ) = x ^T .

Поскольку для линейной динамической системы решение задачи оптимального управления может быть найдено методом моментов [1; 2] (решение, которое при функционалах определенного вида представляет собой идеальное реле), то допустим, что терминальная задача для нелинейной системы может быть решена при функции управления аналогичного типа.

Такая ситуация имеет место в задачах оптимального управления, если управление u входит линейно в гамильтониан H ( x , p , u ) = ф ₁( x , p ) + ф ₂( x , p ) u и управление ограничено по модулю. Так обстоит дело, например, в задаче быстродействия. В этом случае максимизация гамильтониана по u в принципе максимума приводит к соотношению u ^opt( t ) = u _maxsign( ф ₂( x , p )) и, исключая u из краевой задачи принципа максимума, можно, решив двухточечную краевую задачу, решить и задачу оптимального управления.

Часто структура системы управления такова, что исполнительный механизм может действовать по принципу включено-выключено.

Таким образом, в этих случаях структура управления определена с точностью до неизвестных параметров – либо начальных условий для сопряженных переменных p , либо времен переключений управле- ния с точностью до знака управления на первом включении.

Таким образом, для решения задачи необходимо найти функцию вида u (t) =

- A , t e 1 ₁;

A , t e 1 2 ,

где I ₁, I ₂ – множества интервалов, определенных точками переключения, такие, что 1 1 и 1 ₂ = [0, T ]; A -

Пусть R = | r i : r i <  r_{i + 1}, r i e R ⁺ V i = 1, k , r ₀ = 0-множество всех точек переключений, тогда при известном значении функции управления в момент времени определим множества интервалов I ₁, I ₂. Если u (0) <  0, то 1 1 = { ( r ₂ . i _{- 2}, r ₂ . i _{- 1}],2 ■ i - 1 <  card( R ), i eN } и 1 2 = { ( r 2 i _{- 1}, r₂ ii ], 2 ■ i <  card( R ), i e N } , а при u (0) >  0: 1 1 = { ⁽^М, r 2 i L ² ■ i <  ^{Card( R} ), i ^{e N} } и

I 2 = { ⁽ r 2i - 2 , r 2 ^,- 1^] , ² ■ i ^{- 1} <  c ^{ard( R} ), i ^{e N} } .

Таким образом, задачу поиска можно сформулировать следующим образом:

F ( R , A ) = || x ^T - x ( T )| A = A *, R = R *| P m» ,     (3)

при ограничениях r< r+1, rie R +Vi = ____.             (4)

Задачу (3) при ограничениях (4) можно решить с помощью гибридного модифицированного метода эволюционных стратегий [3], при заранее фиксированном числе переключений k. От ограничений типа (4) можно уйти, распределив каждый ген, кроме первого – который будет отвечать за амплитуду начальной популяции на интервале [0, R‘], где R' - любое положительное вещественное число, и изменив операцию мутации oPi,j = |oPi,j+ T,j ■ N(0,sPi,j)|, spi = spi + T ■ N (0,1), где i = 1, N - номер индивида в популяции;

j = 2, n , n - размерность признакового пространства.

Таким образом, случайный поиск будет осуществляться только среди положительных чисел – для точек переключения, на всей числовой прямой – для амплитуды. Для разрешения неравенства r < r+1 представим каждого индивида следующим образом: opi,1 – ____ амплитуда реле, r = ^ opi j+1, i' = 1, k - точки пере-j=1      , ключения.

амплитуда реле.

В итоге управление будет определено по решению задачи на безусловный экстремум (3). Таким образом, в качестве решения мы получим функцию управления с числом точек переключения меньшим либо равным k .

Пример 1. Приведем пример решения двухточечной краевой задачи для системы x' + 2 ■ sin(x) = u(t), x(0) =

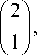
— 3

x ( T ) =       , T = 5.

I 0 J

не менялись. Нелинейное дифференциальное уравне ние решалось методом Рунге—Кутты 4-го порядка точности.

Траектории системы и найденное управление представлены на рис. 1. Конечное состояние системы – x (T) =

Г — 2,997 8 ^ (— 0,001679 5 J .

Пример 2. Рассмотрим задачу с другими условиями:

, 2                           Г 2)

x - x ² + x ■ u ( t ) = 0, x (0) = 1 i I ,

Пусть k = 10. Для 100 индивидов и 50 популяций работы модифицированного алгоритма эволюционных стратегий с локальным спуском: для 10 случайно выбранных индивидов выполняется покоординатный спуск для 5 случайно выбранных генов – 5 шагов величиной 0.05. Настройки алгоритма: турнирная селекция (размер турнира – 10), дискретное скрещивание. Далее перечисленные настройки алгоритма

x (T ) =

— 2

T = 5.

Траектории системы и управление представлены

на рис. 2. Вектор конечного состояния системы

x ( T ) =

Г 3,015 3 ) (— 1,965 5 J .

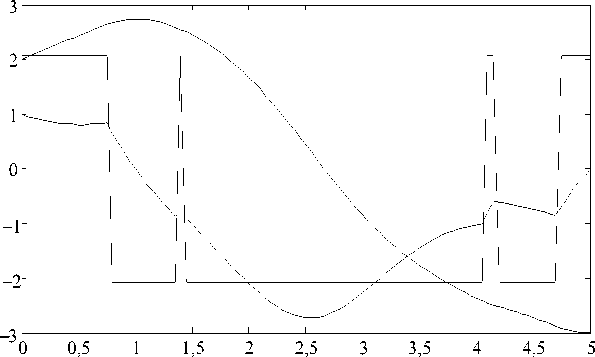
Рис. 1

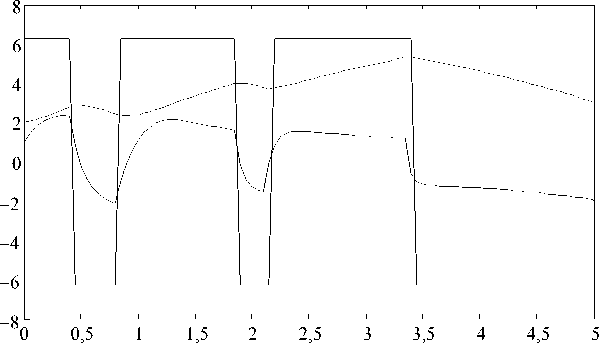
Рис. 2

В том случае, когда нужно найти управление с фиксированным числом точек переключений, опреде- лим множество всех точек переключения следующим образом: R = |ri : ri < ri+1, ri e (0, T] Vi = 1, k, r0 = 0и к ограничениям типа (4) введем еще одно ограничение:

rk < T, или, в иной форме:

k

S op i , j + 1 <  T .

j = 1

Тогда задача поиска будет выглядеть следующим образом:

F ( ^R , A ) = | x T - x (T ) A = A * r = R *|| +

k

+ ^а -ф ( ^ oP i , j + 1

= 1

- T ) ^ min, A *, R *

где ф ( x ) =

П x |, ^x >  ⁰

[ 0, x <  0

– функция штрафа за нарушение ограничений; a - весовой коэффициент.

Приняв a= 10, решим задачи (5) и (6). Конечные состояния    системы,    соответственно

Г - 2,992 4 ) Г 2,999 6 )

x(T) = и x(T) = . Графики (-0,018 241J ; (-1,999 6J траекторий системы и найденного управления представлены на рис. 3 и 4.

Отметим, что в случае когда следующая точка переключения располагается на расстоянии меньшем, чем шаг интегрирования от предыдущей точки, то фактически никаких изменений при данной схеме предыдущая точка не вносит. Происходит своего рода косвенная настройка алгоритмом количества точек переключений, хоть и не такая очевидная и эффективная, как в задаче (3) с ограничениями (4).