Решение уравнений Максвелла для цилиндрической волны в вакууме

В [1] «рассматривается цилиндрически симметричная волновая функция lp(p, t) , где p = (%² + у²)¹ / ² - стандартная цилиндрическая координата. Предполагая, что эта функция удовлетворяет трехмерному волновому уравнению, которое можно переписать в виде

• 5^   .,2 9 2 P   1дф

at²         l ap^{2 +} pdp)’                          ( )

можно показать, что синусоидальная цилиндрическая волна с фазовым углом ф , волновым числом к и угловой частотой to = kv имеет приближенную волновую функцию

ip(p, t) « ^Op-1/2cos(tot — kp — ф)              (539)

в пределе to = kv . Здесь lp_op^-1/2 - амплитуда волны. Соответствующие волновые фронты (то есть поверхности с постоянной фазой) представляют собой набор концентрических цилиндров, которые распространяются радиально наружу от их общей оси p = 0 с фазовой скоростью to/к = V - см. рис. 1. Амплитуда волны затухает как p^-1/2 . Такое поведение можно понять, 115

как следствие сохранения энергии, согласно которому мощность, протекающая через различные поверхности Акр = const. (Площади таких поверхностей масштабируются как Акр . Более того, мощность, протекающая через них, пропорциональна ф 2 Аф² , потому что поток энергии, связанный с волной, обычно пропорционален ф² , и направлена перпендикулярно волновым фронтам.) Цилиндрическая волна, указанная в выражении (539), такова, что генерируется однородным линейным источником, расположенным в точке р = 0 - см. рис. 1.»

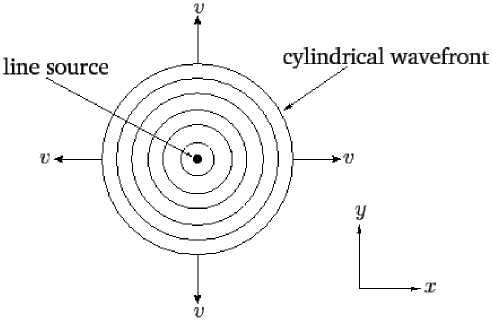
Рис. 1.

Странно, что автор назвал такие волны цилиндрическими. Следовало бы назвать их коническими, т.к. в них волновые фронты -набор концентрических цилиндров, которые распространяются радиально наружу, еще и распространяются вдоль оси: раньше возникшие фронты продолжают расширяться в то время, как возникающие цилиндры начинают расширятся . Оправданием могло бы служить то, что действительно цилиндрические волны, в которых эти цилиндры сохраняют свой радиус, не существуют в природе. Но посмотрите на увеличительное стекло, которым мальчик в полдень разводит огонь — см. рис. 2. Солнечный луч, который входим в лупу, очевидно является цилиндрической волной. Другой пример — лупа Френеля, создающая цилиндрическую волну на выходе — см. рис. 3 из [3]. Известны также цилиндрические линзы, особенность которых — наличие оси, в направлении которой оптическое действие не проявляется [2].

Таким образом, цилиндрические волны , (впрочем, также, как и конические) не могут быть представлены волновой функцией .

Поэтому рассмотрим новую функцию, описывающую цилиндрические волны и являющуюся решением уравнений Максвелла.

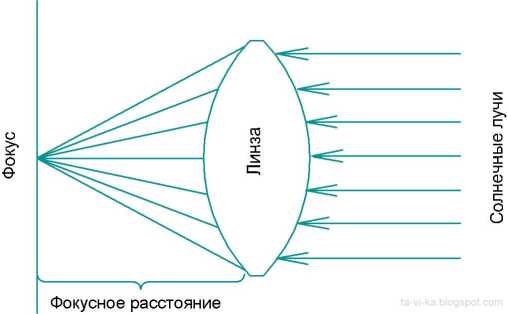
Рис. 2.

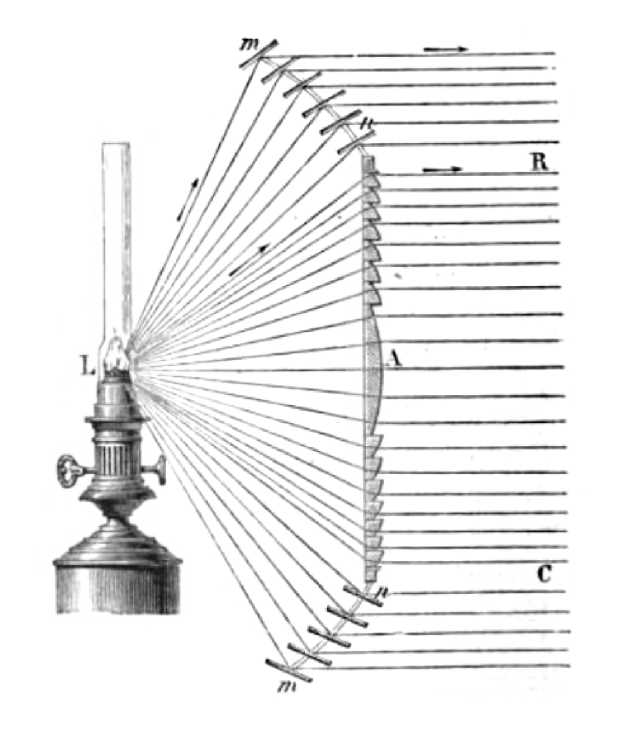
Рис. 3.

Далее будет доказано, что для системы уравнений Максвелла существует решение, описывающее цилиндрическую волну в вакууме. Это решение сохраняет постоянство потока энергии в такой волне и форму этой волны.

2. Решение уравнений Максвелла

Рассмотрим систему уравнений Максвелла для вакуума, которая

имеет вид rot(E) + ^ = 0,                           (а) rot(H) — ^ = 0,                          (b) div(E) = 0,                                          (c) div(H) = 0.                                          (d) B системе ц вид [4]: [илиндрических координат г, р, z эти уравнения имеют Еу । ЭЕГ + 1 . дЕф + dEz _ 0                   /i r + dr + r ‘ дф + dz = ,                 ( ) 1 dEz  дЕф _ ^ОНу r Эф    dz    с dt , дЕг  dEz _ цдИф dz     dr    с dt , Еф । dEФ _1 , dEr   М dHz                     (4) r     dr    r  dф    с dt , Ну + dBr + 1 _ ЭНф + dHz _ 0                /5ч r + dr + r Эф    dz     ,                ( ) 1 dHZ   ЭНф _ e ЕЕТ r dф dz с dt ,                               ( ) dHy_dHz _ еОЕе.                         (7) dz     dr    с dt , Нф + dH^-i^BHHy _ edKz                  (8) r     dr    r Эф    с dt ’ где Er, Еф, Ez — электрические напряженности, Hr, Н^, Hz — магнитные напряженности. В этой главе мы будем искать эти

функции в

следующем виде: Hr . _ Hr (г) • co ,                                       ( 9) Н ф ._ Hv (Г • si ,                                 (10) H z ._ H z (г • si ,                                    (11) Er ._ Er (г) • si ,                                        (12) Е ф ._ Ev (г) • co ,                                   (13)

E z . = E_z (r) • co ,

где co = cos( аф + xz + tot),                       (15)

si = sin( аф + xz + tot) ,                         (16)

и a, X,to - некоторые константы, а функции вида E p (r) являются функциями одного аргумента г . Первоочередная задача состоит в том, чтобы найти решение, в котором поток энергии остается постоянным во времени. Найдем те условия, при которых функции (13-18) удовлетворяют этому требованию.

Известно, что плотность потока электромагнитной энергии -вектор Пойнтинга

5 = тЕ х H ,                                  (17)

где

Т = с/4тт .                                            (18)

В цилиндрических координатах г, ф, z плотность потока электромагнитной энергии имеет три компоненты S_r , S ф , S_z ,

направленные вдоль радиуса, по окружности, вдоль оси соответственно. Они определяются по формуле S=Ы I             ГEpH - EzH^ = т(Е х Н) = т EzHr - ErHz .       (19) |              [ErHv - E^H^ Будем рассматривать случай, когда продольные напряженности отсутствуют, т.е. Hz (r) = 0, Ez (r) = 0. Следовательно, Sr = 0, Sp = 0, т.е. поток энергии распространяется только вдоль оси ozи его плотность равна

	S = S z = n(E r Hv -		E p H)	(20)
или, с	учетом (9-16), S = Sz	= v(E r Hv si2	- EpHr co2).	(21)
Если	ErHv =	= -E(pH r ,		(22)
то	S = Sz	= TE r H p .		(23)

Из (23) с учетом (2) найдем полный поток энергии через сечение волны

	S z = ^^ H rp lE r H p dr^a»)                   (24)
или	S z = VolE r H p -r^dr) .                      (25)

Этот интеграл не зависит от времени. Следовательно, при выполнении условия (22) поток энергии электромагнитной волны является постояным во времени.

Следующая задача состоит в том, чтобы найти вид функций

E_r , Н ф , Е ф , Н_г , удовлетворяющих системе уравнений (1-8) и условию

(22). Перед поиском решений надо отметить, что уравнения Максвелла могут иметь множество решений (как любая система дифференциальных уравнений в частных производных). Некоторые из этих решений нарушают очевидные физические требования, в частности, выполнение закона сохранения энергии. Например, известное решение в виде волновой функции, как известно нарушает этот (в этом решение он сохраняется лишь в среднем во времени, что противоречит самому духу этого закона). Автором найдено решение (см. приложение), в котором соблюдаются известные физические требования. Оно имеет следующий вид:

E_r (r) = Ar^a+lS exp(—8r), (26)

Е ф (r) = E r (r), (27)

H r (r) = -^ ^ E r (r), (28) Н ф (r) = J | E r (r), (29) X = 7V3" (30) 8 > 0, (31)

где A, a, 8 - некоторые константы. Правильность решения можно проверить подстановкой.

В этом решении условие (22) выполняется. Действительно, подставляя (26) в (22), получаем:

Е_гН_ф = -Е_фН_г = A 2 J ^ r²“-2'^:' exp(-28r).        (32)

При этом (25) принимает вид:

R

Sz = 2f ^ЕгНф •r^dr) =

• _r 2a+2' exp(—28r) •r • dr | = A²- — f V(a,8)dr )     ²1 "0

или

S_z = A²

c- Ez(a, 8, R), 2 др

где

У(а, т9) = (r2a+2l9+1exp(—2?9r)), Z(a, 0, R) = /0КУ(а, i9)dr.

Из формулы (26) следует, что радиус цилиндрической волны можно найти из предположения, что радиус волны кончается там, где exp(-?9r) достаточно мало, т.е. равно достаточно малой величине 5. При этом exp(—d R) = 5(36)

или

R «ln-^f2.

Например, при ?9 = 0.46 радиус волны с точностью 1% ln(0.01)

R «-----« 10 sm.(38)

-0.46

Итак, при данном а и ?9 могут быть найдены все параметры воны, включая ее радиус. Следует подчеркнуть, что полученное решение определяет лишь пару значений {а, т? } , но не дает какого-либо соотношения между ними .

Рассмотрим вопрос об определении константы а при данном радиусе R волны или при данном параметре 19 (что, как следует из (37), одно и тоже).

В различных областях физики известны принципы минимума энергии, заключающиеся в том, что система, у которой есть свобода в выборе состояния, приходит в то состояние, при котором минимизируется ее суммарная энергия. Известны, например, принцип, сформулированный Гиббсом, - принцип минимума внутренней энергии; принцип минимума энергии электронов на атомных орбиталях; принцип минимума общей потенциальной энергии деформирующегося тела; найденный Максвеллом принцип минимума тепловых потерь в резистивных цепях.

Мы предлагаем для решения данной задачи использовать принцип минимума потока электромагнитной энергии в электромагнитной волне данного радиуса . Для этого необходимо и достаточно найти минимум величины Z(a, ?9, R) при данном 19 . На рис. 4 показаны для иллюстрации функции

ET(r) = ra+5exp(-?9r),                           (см. 26)

У(а, т9) = ^r2a+2l9+1exp(—2?9r)^.                  (см. 34)

Вычислены также суммы S_rE_r (г, 0) , Z(a, 0, R') ~S_rV(a, 0) и радиус R по (37). Все эти функции и числа определены при данном 0 = 0.7 и различных значениях а . Видно, что сумма Z(a, 0, R") принимает минимальное значение при а = -0 .

alfa=-0.6, d=0.7 SpirArh7

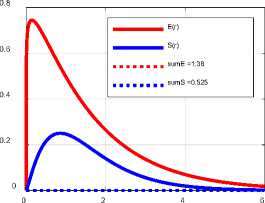
alfa=-0.7, d=0.7, R=4.4 Fig. 4

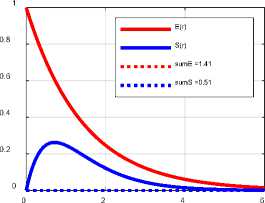
alfa=-0.8, d=0.7

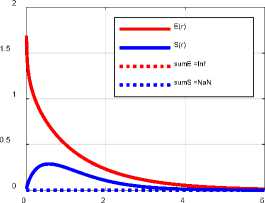
alfa=0.5, d=0.7

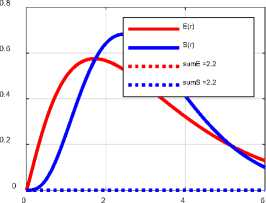
Таким образом, в результате минимизации функции Z(a, 0, R) по переменной а мы находим минимум этой функции. При этом вычисляется также оптимальное значение

а = —0, при котором yCl + 0 — 1

Er (г = 0) = 1.

Это означает, что мы вычисляем

Er(г) +- > ЕГ1т(г) = Дехр(—0г),

Z(a,0,R) ^-^Zzim(a,0,R) = 0.5R2exp(—20R).

Решение (26-31) существует при любом г , что может быть проверено непосредственной подстановкой решения в уравнения Максвелла. Существует, однако, особый случай, когда 122

a + 8 = 0

и подстановка не дает удовлетворительного результата. Однако при

{a + 8 ^ 0} такая проверка выполняется успешно. Поэтому можно утверждать, что при условии (33) напряженность

Ёт (r) = Aexp(-8r), а это именно то значение, которое найдено при оптимизации - см. (42).

Таким образом, можно утверждать, что существует цилиндрическая волна, в которой напряженность Ё_г (r) определяется по (35). Такая волна может возникнуть при одном из двух условий:

• 1.    если определен параметр 8 , по которому в результате природной минимизации определяется параметр a;

• 2.    если определен параметр а , по которому в результате природной минимизации определяется параметр 8 .

Таким образом, теоретически возможны цилиндрические волны различного радиуса и различной частоты, несущие поток электромагнитной энергии различной величины. Остается открытым вопрос, существуют ли естественные процессы, создающие такие волны.

Итак, цилиндрическая волна описывается следующими уравнениями:

Ё_т (r) = Л • exp(ar),                              (46, 39)

Еф (r) = Ёт (r),

Н (r) = —^Л (r),(28)

Н^ (r) = ^Ёг (r),(29)

X =(30)

S_z = A^^J^r • exp(2ar)dr,        (33, 34, 35, 39)

a < 0.                                             (31, 39)

Приложение

Рассмотрим уравнения (2.1-2.16). Непосредственной подстановкой можно убедиться, что функции (2.9-2.14) преобразуют систему уравнений (2.1-2.8) с четырьмя аргументами r, р, z,t в

систему уравнений с одним аргументом г и функциями H(г). Е (г) :	неизвестными
- Е - + ^- i H ^ a-^ = 0 ,	(1)
--r-Eza + ЕфХ-^Нт = 0,	(2)
^X"^+^ = 0.	(3)
-Еф (г)+ ^^- - Era + — Hz = 0. - фк у     dr - '        с	(4)
- H r + d- + - H , a— xH = 0 ,	(5)
- - •H z a-xH ^ -^E - =0 ,	(б)
-ХЕТ + ~ + —Еф = 0 , Л l    dr    с ф	(7)
1H.P + ^--.Hra + — Ez = 0 . - ф     dr -    '       с	(8)
Функции из (2.9-2.14) определим в следующем виде:
Hr (г) = Er(г) • г • ехр(—Аг).	( 9)
Ег (г) = er (г) • г • ехр(—Аг).	(10)
А > 0.	(11)
где E(г). e (г) - некоторые функции координаты г . Заметим, что
J r r = ехр(—Аг)(е - г + (1 — Аг)ег ) ,	(12)
(rr()+ dr ) ) = ех Р ( ^(^ + е- г	— Аег + er) =
ехр(—Аг)(е - г — (А — 2)er).	v       (13)
Используя затем формулы (9-11), преобразуем формулы (1-4) в формулы (14-17) и, сокращая множитель ехр(—Аг). :получим:
—(А — 2)e - + в - г — ae , — х^ = 0 ,	(14)
—ae z + хгеф —^гЕ - = 0.	(15)
Xe - г — e Z г—e z (1 — Аг) — у rE , = 0.	(1б)
—(А — 2)e , + е , г — aer — ~—гEZ = 0.	(1б)
Аналогично преобразуем формулы (5-8) в формулы (18-21):
—(А — 2) h r + Er г + a h ф + x^z = 0 ,	(18)
^ E z — XE , — ye - = 0 ,	(19)
—XE - — E z —E z ( 1 — Аг) + ye , = 0 ,	(20)
—(А — 2)E(y + E(z)г—Er -I--ez = 0. фу        хф             /       с z	(21)
Предположим, что существует такой коэффициент к ,	что
Er = ker ,	(22)

Доклады независимых авторов                      2021 выпуск 53
hq     keq ,	(23)
hz = -kez.	(24)
Выполним замену переменных по (22-24) в уравнениях перепишем их:	(14-21) и
- ( д - 2)ег + e r г - аеф - /^ = 0 ,	(25)
-ae z + /г e q - ^rkeT = 0,	(26)
/етг - e Z г-e z (1 - дг) - ^rke q = 0,	(27)
-( д - 2)eq + e ) г - aer - ^^ rkez = 0.	(28)
-(д - 2)ker - ke Z г - akeq - /гhz = 0 ,	(29)
- ^ k e z + /^e q -^e r = 0 ,	(30)
-/ker + ke z +kez (1 - дг) + ^eq) = 0 ,	(31)
+(д - 2)keq - ke ) г+a ker + £7 ez = 0 .	(32)
Заметим, что уравнения (26) и (30) совпадают при
£7    /лмк	(33)
kc = c .
Следовательно,
k =Л.	(34)

Заметим еще, что уравнения (27) и (31) и уравнения (28) и (32) также совпадают при условии (33). Наконец, уравнения (25) и (29) совпадают. Таким образом, уравнения (29-32) могут быть исключены из системы уравнений. Оставшиеся 4 уравнения (25-28) являются системой дифференциальных уравнений с 3-мя неизвестными

Будем решать систему уравнений (25-28) в предположении, что

Hz . = 0, Ez . = 0.	(35) (36)
Тогда и
hz . = 0,	(37)
ez . = 0.	(38)
При этом уравнения (25-28) примут вид:
(2 - д)er + e'rг - aeq = 0 ,	(39)
/т-e q -k^e r = 0,	(40)
Xe r г - k ^Cг гe q = 0,	(41)
(2 - д)eq + e ) г - aer = 0.	(42)

Из (39, 42) следует

еу    6ф, (43) а из (40, 41) следует (43) и X = ^' (44) Из ((22, 23, 43) следует, что hy     hq ■ (45) Из (44, 34) находим: to 1— X = (46) Из (42, 43) находим: (2 — 8 — а)еу + еУг = 0. (47) или еу = Дга+т9-1, (48) где А - некоторая константа.

Итак, мы нашли функции (2.26-2.31).