Решение уравнения неразрывности консервативным полулагранжевым методом с разными шагами по времени в разных частях вычислительной области
Автор: Вяткин А. В., Мальцев А. Д.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 2 т.24, 2023 года.
Бесплатный доступ
Течение газа, вытекающего из сопла ракеты, описывается системой уравнений Навье - Стокса. Для поиска решения уравнений Навье - Стокса в общем случае используются численные методы. Однако даже современные численные методы не позволяют осуществить моделирование течения газа с учетом всех особенностей течения. Это связано со сложными физическими процессами, возникающими при течении газа из сопла, и ограничением вычислительных возможностей. Существует как минимум два пути решения этой сложности: разрабатывать численные методы, использующие меньшую вычислительную сложность, или повышать производительность вычислительных систем. В связи с этим, целью многих научных исследований является разработка численных методов, которые по отношению к существующим методам требуют меньше вычислительных ресурсов и, одновременно с этим, позволяют находить решение без потери точности. В 1959 г. Aksel C. Wiin-Nielsen представил новый численный метод для решения задачи прогнозирования погоды, названный методом траекторий. В 1966 г. К. М. Магомедов использовал аналогичных подход при разработке численного алгоритма для поиска численного решения задачи, моделирующей трехмерное течение газа. В 1982 г. O. Pironneau развил этот метод для построения численного решения двумерных уравнений Навье - Стокса. В настоящее время эти методы интенсивно развиваются и у них устоялось общее название: полулагранжевы или эйлеролагранжевы методы. Чтобы использовать преимущества этого подхода, ученые раскладывают уравнения Навье - Стокса на три составляющие: конвективная часть (гиперболическая часть уравнений), эллиптическая часть и часть известных величин, которая записывается в правой части уравнений. При решении уравнений Навье - Стокса полулагранжевы методы используются для аппроксимации конвективной части. К этой части относятся все слагаемые уравнения неразрывности. Для разработки численного метода мы будем искать решение уравнения неразрывности. Консервативные версии полулагранжевых методов основаны на теореме Гаусса - Остроградского (теорема о дивергенции в зарубежной литературе). Такой подход позволяет достигнуть выполнения закона сохранения для численного решения задачи в норме пространства L1. Целью нашего исследования является разработка численного алгоритма с использованием разных шагов по времени в разных частях вычислительной области. Это позволит добиться выполнения одновременно трех важных свойств: сходимости численного решения задачи к точному ее решению, снижения вычислительной сложности метода, выполнения закона сохранения без использования поправочных (весовых) коэффициентов. Чтобы построить такой алгоритм, мы разбили одномерную вычислительную область на две части (подобласти), в которых мы используем разные шаги по времени. Основная сложность при разработке алгоритма состоит в поиске численного решения на границах двух подобластей. Одномерное (по пространству) уравнение неразрывности является тестовым уравнением для разработки алгоритма, на котором показана принципиальная возможность создания алгоритма с указанными свойствами. В дальнейших исследованиях этот алгоритм будет обобщен для решения двумерной и трехмерной задач. При моделировании реальных задач описанный подход позволит более точно моделировать течение газа без искусственного размывания, связанного с вычислением интегралов на нижнем слое по времени, в частях вычислительной области с высоким уровнем изменения численного решения
Уравнение неразрывности, полулагранжев метод, закон сохранения массы, сетка с висячими узлами, моделирование течения газа
Короткий адрес: https://sciup.org/148326820
IDR: 148326820 | УДК: 519.633 | DOI: 10.31772/2712-8970-2023-24-2-218-233
Текст научной статьи Решение уравнения неразрывности консервативным полулагранжевым методом с разными шагами по времени в разных частях вычислительной области
В настоящее время задача полноценного моделирования течения газа [1] из сопла ракеты с описанием всех возникающих физических процессов полностью не решена. Основным подходом для поиска решения дифференциальных уравнений, используемых при физикоматематическом моделировании течения газа, является использование численных методов. Одним из препятствий в этом подходе является ограниченная вычислительная мощность вычислительных систем. Решение этой сложности состоит в увеличении мощности вычислительных систем и снижении вычислительной сложности используемых численных методов. Наиболее точно течение газа описывается системой дифференциальных уравнений Навье – Стоксах [2–6]. Эта система включает в себя уравнение неразрывности. Каждое уравнение из системы уравнений Навье – Стокса может быть рассмотрено в терминах конвективных и диффузионных слагаемых [7], а также правой части. Разработанный метод может быть использован для аппроксимации конвективных слагаемых системы уравнений Навье – Стокса. Остальные слагаемые из системы уравнений Навье – Стокса могут аппроксимироваться, например, в соответствии с технологией метода конечных элементов [2] или метода конечных разностей [8]. Идея использовать полулагранжевы методы (ранее эти методы назывались методами характеристик или методами траекторий) для описания течения газа появилась еще во второй половине XX в. [9–11]. В дальнейшем полулагранжевы методы начали использоваться при решение многих других задач [12–14]. Современные версии полулагранжевых методов являются консервативными [12; 15; 16]. При решении уравнения неразрывности под консервативностью, как правило, понимается выполнение закона сохранения для численного решения задачи в норме пространства L 1 . [5; 15]. С точки зрения физики выполнение этого закона сохранения для численного решения уравнения неразрывности означат выполнение закона сохранения массы [1]. Для снижения вычислительной сложности расчетов строятся методы, использующие неравномерную (по пространству) вычислительную сетку [17; 18]. Это позволяет сократить время расчетов или использовать более мелкую сетку для поиска более точного решения. Несмотря на то, что при построении консервативных полулагранжевых методов дифференциальное уравнение неразрывности заменяется интегральным тождеством [15], использование неравномерной сетки, как правило, влечет за собой невозможность достижения локального закона сохранения для окрестностей узлов вычислительной сетки. Поэтому, чтобы добиться выполнения закона сохранения, используются поправочные коэффициенты, которые привносят в алгоритм дополнительную искусственную вязкость. Это существенно снижает точность вычислений в частях вычислительной области с высоким уровнем изменения численного решения.
Целью работы является теоретическое обоснование, программная реализация и подтверждение на основе вычислительных экспериментов алгоритма использования разных шагов по времени в разных частях вычислительной области. Использование такого подхода позволит добиться одновременно трех следующих свойств: сходимости численного решения задачи к точному решению, сокращения вычислительных затрат, выполнения закона сохранения без использования поправочных коэффициентов. Использование различных шагов по времени в разных частях вычислительной области до сих пор развивалось только рамках теории разностных схем и не позволяло достичь выполнения закона сохранения в норме пространства L 1 . В рамках проведенного исследования сформулированы и теоретически доказаны теоремы, а также проведены вычислительные эксперименты. Рассматриваемое одномерное (по пространству) уравнение неразрывности является тестовым для разработки алгоритма, на котором показана принципиальная возможность создания алгоритма с указанными свойствами. В дальнейшем предполагается обобщить алгоритм для решения двумерной задачи. На практике описанный подход позволит более точно моделировать течение газа без искусственного размывания, связанного с вычислением интегралов на нижнем слое по времени, в частях вычислительной области высоким уровнем изменения численного решения.
Постановка задачи
На множестве D = [ 0, T ] х [ 0,1 ] , T > 0, рассмотрим одномерное уравнение неразрывности с ненулевой правой частью
8£ + «иЯ=f (t, х).(1)
dtd
Здесь p ( t , х ) - искомая функция, а функции u ( t , х ) и f ( t , х ) известны. Полагаем, что функции p ( t , х ) и u ( t , х ) достаточно гладкие. Для определенности, будем считать, что справедливы соотношения
u(t’х)|х=0 ^ 0’ U(t’х)|х=1 ^ 0.
Для искомой функции p ( t , х ) зададим начальное условие
Р( t,х )| t=0 =Pinit( х)
и граничное условие
p(t’х)| х=0 = Pleft (t).
Здесь p init ( х ), p left ( t ) - известные функции.
Множество значений Q = [ 0,1 ] переменной х разобьём на два подмножества QT= [ 0;0,4 ] и [ 0,6;1 ] и Q2t= ( 0,4;0,6 ) . На множестве [ 0, T ] х^ т введем равномерную сетку с шагом h = 1 N , N = 10 • 2 n , n - целое положительное число, по оси Ох и шагом т = 1/ M , M -четное положительное число, по оси Ot в следующем виде:
D т = { ( t m , х ): t m = m т , х = ih ; i = 0,..., N 1 , N 2 ,..., N ; m = 0,..., M } , где
N 1 : N 1 h = 0,4 и N 2 : N 2 h = 0,6.
На множестве [ 0, T ] xQ 2 t введем сетку с шагом h = 1/ N по оси Ох и шагом 2 т по оси Ot в виде
D 2 Т = { ( 1 2 m , хj ): 1 2 m = 2 т т ,хj = jh ; j = N 1 + 1,..., N 2 - 1; m = 0,..., M /2 } .
Численное решение p h ( t , х ) задачи (1)-(4) будем искать во всех узлах сетки Dh ’full = D ти D 2 т (рис. 1).
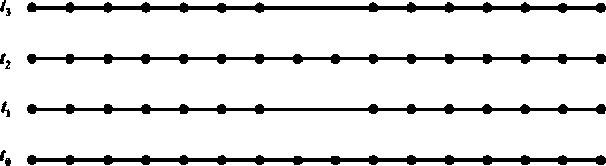
jr = O х = 0,4 х = 0,6 х = 1
Рис. 1. Объединенная вычислительная сетка
Fig. 1. Combined computational grid
Для этого на каждом слое по времени t = tm в каждой пространственной окрестности Q k = [ хк - h / 2, хк + h/ 2 ] п [ 0,1 ] узла ( tm , хк ) сетки Dh ’full искомую функцию p h ( t , х ) определим в виде кусочно-постоянной функции
P h ( t m , x ) = P h ( t m , x k ) V x eQ k .
В дальнейшем для удобства используем обозначения g ( t m , xk ) = g m и p h ( t m , xk ) = p k ’ m . Для упрощения теоретических выкладок полагаем, что т = с h , где с - некоторая константа такая, что
с ------- Г7---xi.
4max u ( t , x )
В общем случае описываемого метода ограничение (6) может быть ослаблено так, что может использоваться константа с большего значения. Однако мы используем это ограничение для упрощения теоретических выкладок.
Интегральное тождество во внутренних узлах сеток
Рассмотрим узел ( tm , xk ) , m > 0; k > 0, при k ^ N 1 , k ^ N 1 + 1 и k ^ N 2 - 1 , k ^ N 2 . В этом случае узел ( tm , xk ) является внутренним узлом сетки D т или сетки D 2 т . Обозначим ( t m , x l ) и ( tm , x r ) - две точки, которые являются границами множества Q k на слое по времени tm . Для каждой из этих точек в плоскости ( t , x ) построим обратно по времени со слоя t = t m на слой t = t m - s характеристическую траекторию C q ( t , x ( t ) ) , q = 1 , r (1). Здесь s = 1, если ( t m , xk ) e D т , и s = 2, если ( t m , xk ) e D 2 т (рис. 2). Каждая траектория является решением задачи Коши для обыкновенного дифференциального уравнения
—q = и ( t , x q ) , [ t € t m - s , t m ] , (7)
dt с начальными данными xq (tm ) = xq ’ q = 1’ r. (8)
В силу ограничения (6) несложно показать, что x l ( t ) e ( xk - 1 , xk ) и x r ( t ) e ( xk , xk + 1 ) (рис. 2). Координаты траектории Cq ( t , 5c(t ) ) при t = tm - s обозначим в виде
A m - s ( A k , m - s , A k, m - s ) = C q ( t m - s , ^ x q ( t m - s ) ) , q = 1 , r Полагаем, что траектории C l и C r не пересекаются, поэтому A ^x’*m - s < A ^x’rm - s . Обозначим G - множество, ограниченное сверху отрезком t m х [ x l , x r ] , траекториями C l и Cr слева и справа, соответственно, и отрезком tm - s х |^ A kx ’ m - s , A^ x , m - s J снизу, как показано на рис. 2. В соответствии с теоремой Гаусса - Остроградского справедлива теорема 1.
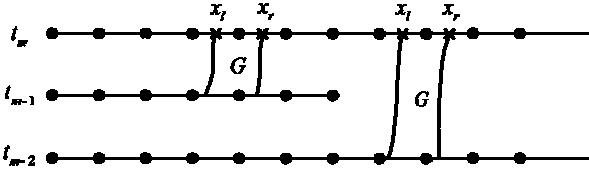
Рис. 2. Характеристические траектории, выпущенные из границ окрестности
Fig. 2. Trajectories issued out from boundary of grid node neighborhood
Теорема 1. Решение задачи (1)–(4) удовлетворяет интегральному уравнению nk
. x , m - s
A k , r
p ( tm , x ) dx = j p ( t m _ s , x ) dx + j f ( t , x ) dtdx .
A x ,
- s
G
Построение численного решения во внутренних узлах сеток
Чтобы построить численный метод, аппроксимируем каждое слагаемое из тождества (9).
Раскладывая функцию p(tm, x) в ряд Тейлора в окрестности точки xk по оси Ox , видно, что d 2Р j Р( tm , x) dx = P( tm , xk ) h '„Л tm , xk )^ + O ( h ) • nk 5x
Для аппроксимации остальных слагаемых из (9) нам потребуется вычислить координаты точек A m - s ( A km - s , A k , m - s ) , q = l , r . Для этого мы решим задачу Коши (7)-(8) численным методом Ньютона
A k,q , m S = x q - s T u ( t m , x q ) , q = l , r ,
где xl = xk - h/2 , xr = xk + h/2 . Таким образом, каждую траекторию мы аппроксимируем пря мой линией, как показано на рис. 3. Определим величину 8mm s такой, что
. x, m - s h, x, m - s k,r Ak,r j P(tm-s,x) dx = j P(tm-s ,x) dx + 8m-"
. x, m - s h, x, m - s k,l Ak,l
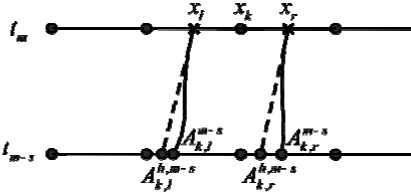
Рис. 3. Аппроксимация траекторий движения прямыми линиями
Fig. 3.Trajectories approximation by straight lines
Справедлива следующая теорема.
Теорема 2. Для приближенного решения (11) задачи (7)–(8) верно
8 m - s = O ( h t2 +t3 ) , q = l , r . (13)
Доказательство.
Не вдаваясь во все точные детали доказательства, представим его в коротком виде. Разложим функцию xcq (t) в окрестности точки t = tm в ряд Тейлора xq ( tm
- sT) = xq (tm )- sTdxq(tm ) + dx"(^q )^Т)-, где ^q G[tm - sT,tm ]• t dt d5„
С учетом тождества -q- (tm) = u (tm, xq), а также с учетом малости величин т и h понятно,
что знак величины
x , m A k , q
j h , 5 , m — s
A k , q
d 5 q ( , \ определяется знаком величины d 2 ( tm ) .
Если величины
2 dxl dt2
(tm )
и
d 2 5r(. x
—r- ( t ) имеют одинаковый знак, например, dt 2 m
положительный
(см. рис. 3), то
Ax ,
'—.
A 5 , m — s
8 m — s k
■m — s , 5 ) d5
‘ m — s , 5 ) d5 .
Ah ,
Ah ,
В этом случае
несложно показать, что 8 mm s = O ( h т 2 +т 3 ) . Если величины
2 dx
( t m ) "
2 dxr dt 2
d 2 5 * dt 2
( t m ) имеют
разные знаки, то существует некоторая точка 5 k е [ 5 l , x r ]
( tm ) = 0 . Тогда, используя разложение в ряд Тейлора, можно показать, что
такая, что
Л 5 , m — s
A k , l
J p ( tm — s , 5 ) d5 = O ( h т 2 +т 3 ) и
A h , 5 , m — s
л 5 , m — s
A k , r
J p ( tm — s , 5 ) d5 = O ( h т 2 +т 3 ) .
A h , 5 , m — s
Тогда из (12) вытекает, что 8 m s = O ( h т 2 + т 3 ) . Теорема 2 доказана.
Аналогично теореме 2, из разложения в ряд Тейлора функции f (t, 5) можно показать, что при использовании соотношения т = с h справедливо tm 5r ( t )
j f ( t , 5 ) d5dt = J dt J f ( t , 5 ) d5 = s T meas ( Q * ) f ( tm , 5Z ) + O ( h 3 ) ,
G
t m — s т 5 1 ( t )
где meas ( Q к ) - длинна окрестности Q к , которая определяется в виде
, . I h , если к = 1,..., N — 1; mes ( Q * ) = <
-
2 [ h /2, если к = 0, к = N .
Подставив (10), (12), (14) в (9), мы получим формулу для вычисления численного решения
Р к л h, 5,, m — s
A k , r
Р * ’ m =------\ J Р h ( t m — s , 5 ) d5 + s т f ( t m , 5 ) .
meas (Q к ) Ah , 5 , m — s
Напомним, что функция p h ( tm — s , 5 ) является кусочно-постоянной, поэтому ее интеграл легко вычисляется аналитически. Исходя из построения алгоритма, формула (15) применима для всех узлов сетки D h ,full при нечетном числе m . Если же m четное число, то формулу (15) можно применять V к > 0: к ^ N 1 , к ^ N 1 + 1, к ^ N 2 — 1, к ^ N 2.
Построение численного решения на границах между сетками
Рассмотрим случай границы между сетками D т и D 2 т при x = 0,6. На границе x = 0,4 алгоритм строится аналогично. Определим способ вычисления численного решения для р Nm и р hN™_\ при четном числе m . В зависимости от знака величины u ( t m , x N 2 - h /2 ) возможны три случая. В первом случае, когда u ( tm , xN 2 - h /2 ) = 0, для вычисления р Nm - 1 , р Nm следует использовать формулу (15).
Пусть u (tm, xN2 - h /2)> 0, тогда ANNxm-1 < xN2 - h /2, как это показано на рис. 4. В этом случае величина р^-1 определяется по формуле (15) при 5 = 2. Чтобы вычислить значение рNm , также используем формулу (15) при 5 = 1 и получим j h, x, m -1
1 AN2 ,r рN2m = J р h (tm-1, x) dx + Tf (tm ’ xN2 ) . (16)
h h , x , m - 1
A N 2, l
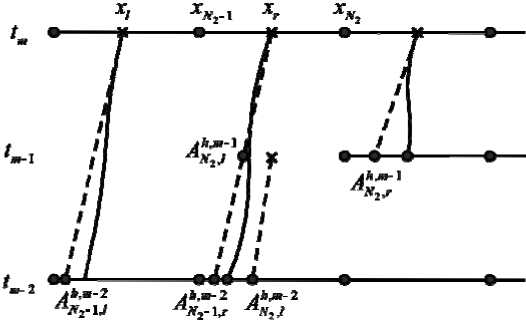
Рис. 4. Случай положительного значения функции скорости на границе x = 0,6 двух сеток
Fig. 4. The case of positive value of velocity function on boundary x = 0,6
Функция рh (tm-1, x) не определена (ранее не вычислена) на всем множестве |^ ANN,2’™-1, ANN-x’m-1J, поэтому вычисление этого интеграла невозможно. Множество |^ AN2’™-1, ANx’m-1J разобьем на два отрезка |^xN2 - h /2, AN,2’m-1J , на котором функция рh (tm-1, x) определена и оставшийся отрезок |^ AN2’™-1,xN2 - h / 2J (рис. 4). Однако, по аналогии с теоремой 1, можно показать, что xN2 -h/2A
J р ( t m - 1 ’ x ) dx = J р ( t m - 2
д h ’ x ’ m-1
AN2 ,l
-
x ) dx + J f ( t , x ) dtdx .
m - 1
GN 2
Здесь величина A m 1 « A N,x’m 2, A m 2 « A N,xm r 2 . В итоге подставим (17) в (16) и получим
. h , x , m - 1 h , x , m - 2
1 A N 2, r 1 A N 2, l
P Nm = J P h ( t m - 1 , x ) dx + J P h ( t m - 2 , x ) dx + T f ( t m ’ x N 2 ) • (18)
h rAr -A/2 h Ji , x , m -2
x N 2 h/2 A N2’- 1, r
Рассмотрим второй случай, когда u (tm, xN2 - h / 2 )< 0 и AN2’m-1 > xN2 - h /2 (рис. 5). В этом случае величина рNm определяется по формуле (15) при s = 1. Чтобы вычислить значение PNm-1, используем формулу (15) при s = 1 и получим j h, x, m-1
1 A N 2 - 1, r
P Nm - 1 = h J P h ( t m - 1 ’ x ) dx + T f ( t m ’ x N 2 ) . (19)
. h , x , m - 1
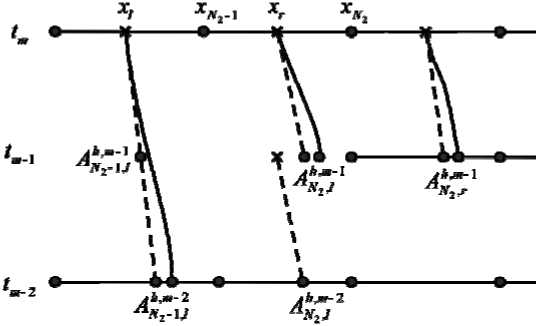
Рис. 5. Случай положительного значения функции скорости на границе x = 0,4 двух сеток
Fig. 5. The case of negative value of velocity function on boundary x = 0,6
Отрезок [ AN2x-m’l 1, ANx’^1 ] разложим на две части: [ AN’x-m/, xn2 -1 + h/2] и [xn2 -1 + h /2, ANx-m-1 ]. Значение функции рh (tm-1, x) на отрезке [xn2 -1 + h /2, ANx-m-1 ] определено. Вновь, по аналогии с теоремой 1, можно показать, что xN2 -1+ h/2
J p(tm-1,x)dx = J p(tm-2,x)dx + J f (t,x)dtdx.(20)
. h, x, m-1 m-2
A N 2 -1,l A l G N 2
Причем, ^A m - 2 ® Ah'x ’ m - 2 , ^A m - 1 ~ A h ’ x ’ m - 2 . Используя (19) и (20) определим
’ l N 2 -1, l ’ r N 2, l д h, x, m-1 h, x, m-2
1 A N 2 - 1, r 1 A N 2, l
P N™1 = h J P h ( t m - 1 ’ x ) dx + h J P h ( t m - 2 ’ x ) dx + 2 t f ( t m ’ x N 2 - 1 ) • (21)
x N 2 - 1 + h /2 A N 2 - m - 2
Закон сохранения и сходимость
Проверку выполнения закона сохранения выполним только на четных слоях по времени, поскольку только на этих временных слоях численное решение рh определено Vx е [0,1]. Классический закон сохранения массы при переходе с текущего слоя по времени на следующий слой с учетом границ втекания, вытекания и функции правой части (внутренних источников) имеет следующий вид [1]:
1 1 t m t m t m 1
j p ( t m ,x ) dx = j p h ( t m - 2 , x ) dx + j p ( t ,0 ) u ( t ,0 ) dt - j p ( t ,1 ) u ( t ,1 ) dt + j dt j f ( t,x ) dx. (22)
0 0 t m - 2 t m - 2 t m - 2 0
Покажем, что тождество (22) справедливо для построенного численного решения р h ( t , x ) .
В соответствии с (15) выпишем формулу для вычисления численного решение на слое t = t m - 1 в узлах сетки D т V k = 1,..., N 1 , N 2 ,..., N :
. h , x ,, m - 2
A k , r
P k , m - 1 =------ TTM J P h ( t m - 2 , x ) dx + T f ( t m - 1 , xk ) . (23)
meas (Q k ) , h , x , m - 2
A k , l
Просуммируем (23) по всем k = 1,..., N 1 , N 2,..., N . С учетом того, что р h ( t , x ) является кусочно-постоянной функцией в каждой окрестности узла xk , мы получим
0.4 + h /2 1
j P h ( t m - 1 , x ) dx + j P h ( t m - 1 , x ) dx = h /2 0.6 - h /2
, h , x„ m - 2 h , x ,, m - 2
N l, r A N , r 0.4 + h /2 1
= j P h ( t m - 2 , x ) dx + j P h ( t m - 2 , x ) dx + T j f h ( t m - 1 , xk ) dx + T j f h ( t m - 1 , x ) dx . (24)
. h , x , m - 2 .h , x , m - 2 h /2 0.6 - h /2
A 1, l A N 2, l
Аналогично теореме 1, можно показать, что на промежутке времени [tm-2, tm-1 ] справедливы тождества, учитывающие втекание и вытекание субстанции h/2 tm-1 Ax’m 2 tm-1 xr (t)
j p ( tm - 1 , x ) dx = j p ( t ,0 ) u ( t ,0 ) dt + j p ( tm - 2, x ) dx + j dt j f ( t , x ) dx ,
0 tm -2 0 tm-2
-
1 tm-1 tm-1
j p(tm-2,x)dx = j p(t,1)u(t,1)dt + j dt j f (t,x)dx.
AN,m ”2 tm - 2 tm - 2 xl ( t )
С учетом (25) определим р h ( tm - 1 , x 0 ) и р h ( t ,1 ) uh ( t ,1 ) такими, что
. h , x , m - 2
h tm-1 ^0, r
-
- P h ( t m - 1 , x 0 ) = j P h ( t ,0 ) u h ( t ,0 ) dt + j P h ( t m - 2 , x ) dx + TT f ( t m - 1 , x 0 ) ,
-
2 tm-2 0
0.4+h/21
tm-1
j Ph (t,1)uh (t,1)dt = j Ph (tm-2,x)dx.(26)
t m - 2 A Nxm - 2
Добавим тождества (26) в (24) и получим
j p h ( t m - 1 , x ) dx + j p h ( t m - 1 , x ) dx =
0 0.6 - h /2
. h , x,, m — 2
'—.
. 2, x) dx + J p h (tm - 2, x) dx — j h, x, m—2
A N 2, l
t m — 1 N 1,r
= J ph (t,0) uh (t,0) dt + J ph (t, tm—2 0
t m — 1 0.4 + h /2 1
— J p h ( t ,1 ) uh ( t ,1 ) dt + t J fh ( t m — 1 , xk ) dx + t J fh ( t m — 1 , x ) dx.
t m — 2 0 0.6 — h /2
С одной стороны, значения функции p ( t , x ) на границе x = 0 нам известны, а с другой - для выполнения закона сохранения мы использовали p h ( tm — 1 ,0) из первого соотношения в (26). Чтобы одновременно добиться выполнения сохранения и использовать точное решение на границе втекания, определим величину
E(tk—1,0) = p(tk—1,0) —ph (tk—1,0).(27)
Тогда использование точного решение на границе втекания приводит закон сохранения к виду
0.4+h/21
J p h ( t m — 1 , x ) dx + J p h ( t m — 1 , x ) dx = 0 0.6 — h /2
^ h , x ,, m — 2
tm—1 N1,r 1
= J ph ( t,0 ) uh ( t,0) dt + J ph ( tm—2, x ) dx + J ph ( tm—2,x) dx + - E(tm—1,0) — tm—2 0 Ah ’x ',m—2
N2,l tm—1 0.4+h/21
— J ph (t ,1) uh (t ,1) dt + t J fh (tm—1, xk) dx + t J fh (tm—1, x) dx.(28)
tm — 2 0 0.6 — h /2
Проведя аналогичные выкладки для численного решения на слое t = tm в узлах сетки D т V k = 1,..., N 1 , N 2,..., N , мы получим формулу аналогичную (28). Для внутренних узлов D 2 т при k = N 1 + 2,..., N 2 — 2 после суммирования (15), получим
-
д h , x , m — 2
N 2 — 2 + h /2 A N 2, r N 2 — 2 + h /2
J p h ( t m , x ) dx = J p h ( t m — 2 , x ) dx + 2 t J fh ( t m , x ) dx . (29)
N + 2 — h /2 hh , x , m — 2 N + 2 — h /2
N 1, l
С учетом специфики построения формул для вычисления численного решения на четном слое t = tm для k = N 1 , N 1 + 1, N 2 — 1, N 2 и используя (28)-(29), получим
-
1 tm —1
Jph (tm,x)dx = J ph (t,0)uh (t,0)dt + Jph (tm—2,x)dx + 0 tm—2
tmtm 1
+ 2 E (tm ,0) + 2 E (tm—1,0) — J p h (t ,1) uh (t ,1) dt + J dt J fh (t, x) dx.(30)
t m — 2 t m — 2 0
Тождество (30) представляет собой закон сохранения для искомой функции p h при переходе с временного слоя t = tm — 2 на слой t = tm с учетом втекания через границу x = 0 , вытекания через границу x = 1, внутренних источников, описываемых функций f ( t , x ) и корректировки закона сохранения в виду использования точного решения на границе втекания.
Для проверки сходимости численного решения к точному решению задачи (1)–(4) используем норму пространства L 1 :
N errn (tm )= Ph (tm , x )-P( tm, x), = E meas (Q k )P k, m -Pm ' (31)
1 k = 0
С учетом выполнения закона сохранения и наличия аппроксимации интегрального тождества (9) с точностью O ( h 3 ) при выполнении равенства т = с h несложно показать [13], что численное решение задачи (1)–(4) сходится к точному решению с первым порядком точности.
Результаты вычислительного эксперимента
Чтобы протестировать разработанный алгоритм, была проведена серия вычислительных экспериментов. Для одного из них использовались следующие функции
р ( t , x ) = 1,1 + sin ( t x ) , u ( t , x ) = 0,6 + 0,5cos ( 2 n x ) .
Используя функции (32), были заданы функции Pinit(x), Pleft(t) и f (t,x). После этого была сформулирована задача (1)-(4). Решение задачи искалось на серии сеток при N = 10 ■ 2n , n = 1,...,6. Для удовлетворения ограничения (6) использовалось тождество т = 0,2 h . Для оценки погрешности errn (tm) численного решения используем норму (31). Порядок сходимости численного решения к точному решению оценивается параметром convn = log2 (errn-1 (T) / errn (T)). Результаты расчетов приведены в табл. 1. Из таблицы видно, что алгоритм имеет первый порядок сходимости.
Таблица 1
О порядке сходимости разработанного метода
|
n |
N |
M |
errn ( T ) |
conv n |
|
1 |
20 |
100 |
0,0234467 |
|
|
2 |
40 |
200 |
0,0103564 |
1,17646 |
|
3 |
80 |
400 |
0,0048117 |
1,10544 |
|
4 |
160 |
800 |
0,0023115 |
1,05774 |
|
5 |
320 |
1600 |
0,0011317 |
1,03027 |
|
6 |
640 |
3200 |
0,0005598 |
1,01542 |
Для проверки выполнения закона сохранения на каждом четном слое по времени были отдельно вычислены следующие величины:
-
- масса газа на слое по времени t = t m
1N massm = Jph (tm, x) dx = £ meas (Qk )pk,m ;
0 k = 0
-
- масса жидкости, которая втекла через границу втекания x = 0 за время [ t m - 2, t m ] ,
inPut m = ^ P left ( t m - 2 ) u ( t m - 2 ,0 ) + T P left ( t m - 1 ) u ( t m - 1 ,0 ) + ^ P left ( t m ) u ( t m ,0 ) ;
-
- масса жидкости, которая вытекла через границу вытекания x = 1 за время [ tm - 2, tm ] ,
outPut m = J P h ( t m - 2 , x ) dx + J P h ( t m - 1 , x ) dx ;
. h , x , m - 2 .h , x , m - 1
A N , r A N , r
-
- масса жидкости, которая втекла из внутренних источников за время [ t m - 2, t m ] ,
m N 1 - 1 mN N 2 - 1
source m = t Z Z meas (Q k ) f q +t Z Z meas (Q k ) f q + 2 t h Z f m ;
q = т - 1 k = 1 q = т - 1 k = N 2 k = N + 1
-
- коэффициент корректировки в связи с использованием точного решения на границе втекания
hh corr m = 2 р ( t k - 1 ,0 ) + 2 р ( t k ,0 ) - input m ;
-
- коэффициент, показывающий погрешность выполнения закона сохранения, conlow m = mass m - ( mass m - 2 +input m - output m + source m + corr m ) .
Результаты расчетов для N = 20 представлены в табл. 2. Как видно из расчетов, закон сохранения массы выполняется при переходе с каждого четного слоя по времени на следующий четный слой с точностью до представления нуля в машинной арифметике.
Таблица 2
О выполнении закона сохранения
|
m |
mass m |
mass m - 2 |
input m |
output m |
source m |
corrm |
conlow m |
|
2 |
1,124607 |
1,10 |
0,0605 |
0,060827 |
0,026348 |
–0,001415 |
3,13E-15 |
|
4 |
1,149764 |
1,124607 |
0,0605 |
0,062812 |
0,029021 |
–0,001552 |
1,88E-15 |
|
6 |
1,174822 |
1,149764 |
0,0605 |
0,065404 |
0,031652 |
–0,001690 |
2,06E-15 |
|
8 |
1,199616 |
1,174822 |
0,0605 |
0,068115 |
0,034235 |
–0,001827 |
–4,20E-15 |
|
10 |
1,224083 |
1,199616 |
0,0605 |
0,070831 |
0,036763 |
–0,001965 |
8,02E-17 |
|
94 |
1,481967 |
1,463581 |
0,0605 |
0,099126 |
0,060626 |
–0,003615 |
6,94E-15 |
|
96 |
1,499675 |
1,481967 |
0,0605 |
0,100956 |
0,061916 |
–0,003752 |
1,39E-15 |
|
98 |
1,516679 |
1,499675 |
0,0605 |
0,102682 |
0,063077 |
–0,003891 |
–2,49E-15 |
|
100 |
1,532958 |
1,516679 |
0,0605 |
0,1043 |
0,064106 |
–0,004027 |
3,51E-15 |
Заключение
В работе предложен оригинальный подход вычисления решения уравнения неразрывности на вычислительной сетке, состоящей из двух частей, в которых используются разные шаги по времени. Отличительной особенностью построенного метода является выполнение закона сохранения для численного решения в норме L 1 без различного рода поправочных коэффициентов, широко используемых в адаптивных сетках при реализации полулагранжего метода. На практике такой подход позволит более точно моделировать течение газа без искусственного размывания субстанции, связанного с вычислением интегралов на нижнем слое по времени, в частях вычислительной области с высоким уровнем роста численного решения. В дальнейшем предполагается обобщить описанный алгоритм для решения двумерной (по пространству) задачи.
Acknowledgment. This work is supported by the Krasnoyarsk Mathematical Center and financed by the Ministry of Science and Higher Education of the Russian Federation in the framework of the establishment and development of regional Centers for Mathematics Research and Education (Agreement No. 075-02-2023-912)
Список литературы Решение уравнения неразрывности консервативным полулагранжевым методом с разными шагами по времени в разных частях вычислительной области
- Лапин Ю., Стрелец М. Внутренние течения газовых смесей. М. : Наука, 1989. 368 с.
- Combination of Semi-Lagrangian Approach and Finite Element Method for Navier-Stokes Equations / A. V. Vyatkin, E .V. Kuchunova, M. V. Yakubovich et al. // AIP Conference Proceedings. 2020. Vol. 2293. Art. 420057. Doi: 10.1063/5.0026942.
- Bonaventura L., Ferretti R., Rocchi L. A fully semi-Lagrangian discretization for the 2D incompressible Navier-Stokes equations in the vorticity-stream function formulation // Appl. Math. Comput. 2018. Vol. 323. P. 132–144. Doi: 10.1016/j.amc.2017.11.030.
- Shaydurov V. V., Yakubovich M. V. Semi-Lagrangian Approximation of Conservation Laws of Gas Flow in a Channel with Backward Step // Smart Modeling for Engineering Systems. GCM50 2018. Smart Innovation, Systems and Technologies. 2019. Vol. 133. P. 246–265. Doi: 10.1007/978-3-030-06228-6_21.
- A mass-conservative semi-implicit volume of fluid method for the Navier–Stokes equations with high order semi-Lagrangian advection scheme / M. Tavelli, W. Boscheri, G. Stradiotti et al. // Computers & Fluids. 2022. Vol. 240. Art. 105443. Doi: 10.1016/j.compfluid.2022.105443.
- Shaydurov V. V., Shchepanovskaya G. I, Yakubovich M. V. Semi-Lagrangian approximation of conservations laws in the flow around a wedge // Lobachevskii Journal of Mathematics. 2018. Vol. 39, № 7. P. 936–948. Doi: 10.1134/S1995080218070193.
- Barrett A., Fogelson A. L., Griffith B. E. A hybrid semi-Lagrangian cut cell method for advection-diffusion problems with Robin boundary conditions in moving domains // Journal of Computational Physics. Elsevier BV. 2022. Vol. 449. Art. 110805. Doi: 10.1016/j.jcp.2021.110805.
- Huang C., Arbogas T., Qiu J. An Eulerian-Lagrangian WENO finite volume scheme for advection problems // J. Comput. Phys. 2012. Vol. 231. P. 4028–4052. Doi: 10.1016/j.jcp.2012.01.030.
- Магомедов К. М. Метод характеристик для численного решения пространственных течений газа // Журнал вычислительной математики и математической физики. 1966. Т. 6, № 2. С. 313–325.
- Pironneau O. On the transport-diffusion algorithm and its application to the Navier-Stokes equations // Numer. Math. 1982. Vol. 38. P. 309–332. Doi: 10.1007/BF01396435.
- Wiin-Nielsen A. On the application of trajectories methods in numerical forecasting // Tellus. 1959. Vol. 11. P. 180–196. Doi: 10.3402/tellusa.v11i2.9300.
- Crouseilles N., Mehrenberger M., Sonnendrucker E. Conservative semi-Lagrangian schemes for Vlasov equations // J. Comput. Phys. 2010. Vol. 229. 1927–1953. Doi: 10.1016/j.jcp.2009.11.007.
- Shaydurov V. V., Vyatkin A. V., Kuchunova E. V. Semi-Lagrangian difference approximations with different stability requirements // Russian J. Numer. Anal. Math. Modelling. 2018. Vol. 33, №. 2. P. 123–135. Doi: 10.1515/rnam-2018-0011.
- A semi-Lagrangian splitting method for the numerical simulation of sediment transport with free surface flows / S. Boyaval, A. Caboussat, A. Mrad et al. // Comput. Fluids. 2018. Vol. 172. P. 384–396. Doi: 10.1016/j.compfluid.2018.04.002.
- Iske A., Kaser M. Conservative semi‐Lagrangian advection on adaptive unstructured meshes // Numerical Methods for Partial Differential Equations. 2004. Vol. 20 (3). P. 388–411. Doi: 10.1002/num.10100.
- Boscheri W., Tavelli M., Pareschi L. On the Construction of Conservative Semi-Lagrangian IMEX Advection Schemes for Multiscale Time Dependent PDEs // Journal of Scientific Computing. Springer Science and Business Media LLC. 2022. Vol. 90. Art. 97. Doi: 10.1007/s10915-022-01768-0.
- Boscheri W. High order direct arbitrary-Lagrangian-Eulerian (ALE) finite volume schemes for hyperbolic systems on unstructured meshes // Arch. Comput. Methods Eng. 2017. Vol. 24. P 751–801. Doi: 10.1007/s11831-016-9188-x.
- Boscheri W. A space-time semi-Lagrangian advection scheme on staggered Voronoi meshes applied to free surface flows // Comput. Fluids. 2020. Vol. 202. Art. 104503. Doi: 10.1016/j.compfluid.2020.104503.


