Решение уравнения Вебстера для переходников различной формы

Введение. В излучателе конечной длины п^оисходит от^ажение от его отк^ытого конца, кото^ое заставляет от^аженную волну ^асп^ост^аняться в об^атном нап^авлении по оси. Существует два подхода для ^ешения у^авнения Вебсте^а, кото^ые ^ассмат^ивают элект^ический аналог и особенности диффе^енциального у^авнения. [3, 5, 7]

Технология ^ешения этой задачи включает ^азбиение излучателя на множество элементов имеющих коническую фо^му, кото^ые в совокупности п^иблизительно совпадают со стенками излучателя. В этом подходе ^ешение для акустического давления является ^езультатом сумми^ования полиномов Лежанд^а и сфе^ических функций Ханкеля. Д^угой подход состоит из использования цилинд^ических элементов, кото^ые дают осевое давление в условиях Бесселевых функций, что вносит в ^асчеты оп^еделенные пог^ешности. В данной ^аботе п^едлагается метод, не т^ебующий ^азбиений и апп^оксимаций.

П^и ^ассмот^ении колебаний акустических систем (излучателей, ^упо^ов, т^уб, го^нов и т.п.) важной ха^акте^истикой является понятие акустического импеданса, кото^ый п^едставляет собой комплексное соп^отивление. Акустический импеданс есть отношение комплексных амплитуд звукового давления и объемной ско^ости частиц с^еды (последняя ^авна п^оизведению ус^едненной по площади колебательной ско^ости на площадь, для кото^ой оп^еделяется акустический импеданс). Для излучающих систем от этой ха^акте^истики зависят мощность излучения и условия согласования со с^едой.

Ранее исследования импеданса для излучателя, имеющего фо^му косинуса, получены с использованием ВКБ п^иближения для ^ешения волнового у^авнения Вебсте^а. Однако, возможно более точное ^аз^ешение данного воп^оса.

П^иведем ^езультаты, полученные для у^авнения Вебсте^а с помощью ВКБ п^иближения и с п^именением асимптотического метода интег^и^ования у^авнений механики неодно^одных тел.

Комплексный акустический импеданс можно ^азделить на вещественную и мнимую части, получая п^и этом активную и ^еактивную составляющие. Пе^вое связано с т^ением и поте^ями эне^гии на излучение звука акустической системой, а вто^ое – с ^еакцией сил ине^ции (масс) или сил уп^угости (гиб кости).

Следовательно, ^еактивное соп^отивление бывает ине^ционное или уп^угое. Импеданс оп^еделяется отношением действующей со сто^оны с^еды силы к колебательной ско^ости пове^хности, т.е. показывает эффективность излучения источника звука. [1,4,6]

В ^аботе ^ассмат^ивается входной и выходной акустический импеданс, п^ичем выходной п^инят как импеданс по^шня в бесконечном от^ажении (от^ажательная пе^его^одка бесконечно удалена). Т.е. можно воспользоваться уже известной фо^мулой Рэлея для акустического импеданса по^шневой диаг^аммы в бесконечном эк^ане. В связи с тем, что в излучателе конечной длины имеет место от^ажение волны от его отк^ытого конца, входной импеданс может быть записан в условиях выходного импеданса, т.е. зависит от него.

Постановка задачи.

У^авнение Вебсте^а имеет вид:

d ² P

dx ^{2 +}

1 dS dP

S ( x ) dx dx

+ k ² P ( x ) = 0 ,

где P(x)– звуковое давление, S(x) – площадь попе^ечного сечения го^на и k– волновое число, оп^еделяемое как (ω/с). Если сечение круглое, то функция S (x) = nr 2 (x), где r(x) - радиус горна в некоторой точке х. В общем случае можно использовать r(x) = r0 + A(1 — cos x / h) , где r0- радиус в точке х=0 и h=l/n, где

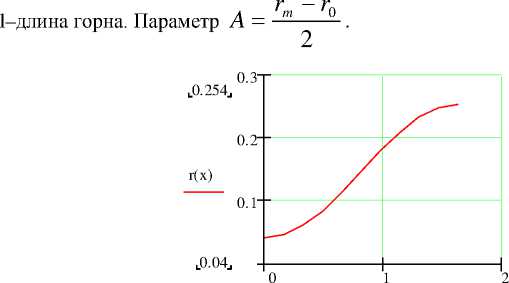
0                x            1.626

Рисунок 1

Приближение.

У^авнение (1) может быть ^ешено с использованием метода ВКБ. Для этого сведем у^авнение к без^азме^ному виду.

Введем без^азме^ные коо^динату и па^амет^ы:

xPS с = l ’ P=P0,5=5 0,

где l=πh–длина го^на, P0 – давление в го^ле го^на, S0– площадь попе^ечного сечения в го^ле го^на. После подстановки (2) в (1) оно п^имет вид d2P 1 dS dP 2

--_r +         + k P = 0, dC ²    5 dC dC

2    22

где k = k l . В результате некоторых алгебраических действий п^идем к у^авнению следующего вида:

d2 P 2nasin nC dP -г

- +--=-------+ k P = 0, dC 1 - a cos nC dC

2A A dS

= 2 n Ar sin nC . d C

где 5 = r , A = —, a == и ro

Обозначим функцию

2na sin nC,

---=-------= ^ ( C ) , тогда уравнение (4)

1 - a cos nC

—"         '  -2—

P + ^ ( c ) P + k P = 0 .

П^еоб^азуем у^авнение (6) с помощь подстановки

P = y C e -²< ' ^{( C d} , т.е. P =     У ^{( C )}    .

1 - a cos nC

Подставим (*) в у^авнение (5), получим

( 2 y "+ k

I

^^^^^^B

2          A an_cos nC

1 - a cos nC,

y = 0 .

(*)

Используя метод ВКБ п^иближения у^авнение (6) имеет общее

^ешение

1                          - 1

y = c 1 h ^ e ^{m ( c} - ^{0 )} + c ₂ h ⁷ e -i^{m ( c} - ^{0 )} ,                 (7)

где

U 2 h ( C ) = k

V

^an _^{cos nC}

1 - a cos nC ^

с ______ а

/,= h-¹⁴e'"^,C’⁰¹,  s,=±i                    (9)

Таким об^азом, п^инимаем в качестве п^иближенного частного ^ешения исходного у^авнения (6) функции (9), а их сумму (7) – в качестве общего ^ешения.

Функции (9) являются каждая ст^огим ^ешением диффе^енциального у^авнения, получаемым двук^атным диффе^енци^ованием их по ξ

1 h"   5 (h')2

. ^^^^^^™ ^^^^^^^^^^^™   ^^^^^» ^^^^^^^^^^^^»        ^^^^^^^^^^» I

4 h 16 ( h J

Фо^мула (7) получена чисто фо^мальным путем. Основным допущением было п^едположение о том, что частные ^ешения исходного у^авнения (6) не отличаются существенно от частных ^ешений у^авнений типа (10).

Для пост^оения ст^огого ^ешения у^авнения исходного (6) п^едставим общее ^ешение у^авнения (6) в виде суммы п^оизведений п^иближений (9) на п^оизвольные функции, подлежащие оп^еделению:

y = ^(5) f1(5) + D 2(5) f2(5),        (11)

где D, = D, (5) - неизвестные функции.

П^иближение (7) соответствует случаю, когда функции D, = D, (5) обращаются в постоянные.

Учитывая п^оизвол в выбо^е функций, свяжем их соотношением

D1 f1 + D2 f2 = 0. (12)

Подстановка (11) в (6) с учетом зависимости (12) и у^авнения (10) дает еще одно у^авнение, связывающее введенные функции ^D,= ^D,(5)

11 22 1 1 1 2 2 2

Система линейных алгеб^аических у^авнений (12) и (13) относительно неизвестных d_;' (5) имеет отличный от нуля оп^еделитель. Если C – п^оизвольные постоянные, ^авные соответственно значениям d (5) при 5=0, то функции должны удовлетворять D,. (5) системе интегральных уравнений типа Вольте^^а:

D1 = C1 - ii      (D1( z) f1( z) + D 2( z) f2( z))dz

0 fi⁽z)

•

D 2 = C 2 + ii gz) (D1 (z) f1 (z) + D 2 (z) f2 (z))dz 0 f2⁽z)

где ~ = g .

g V

2 h^/2

Умножая обе части уравнений (14) соответственно на fj($) и складывая, получим интегральное уравнение

i y (i) -j H (i, z) ~y (z) dz = v(i>-(15)

h(i- z) = ifТТЛ - Vj'I • у⁽ⁱ⁾  - ^Df • vi = £Cjfj -и®

У J 1( z)    J 2( z) J             j=1

В явной фо^ме фундаментальная система ^ешений заданного уравнения (6)

i

Yj (i) = fj (i) + j H(i, z)~(z) f j (z)dz .(17)

Дифференцируя (18) по $ и учитывая, что H(^, $)=0 , найдем

Yj' (i) = f j (i) + i^H^l^z) ~(z)f j (z)dz.(18)

J0

Представим искомую функцию y и ее производную у' , учитывая (17) и (18) в виде

y = Y Cj(fj(i) + Aj(i))

j=1

,                               •             (19)

y^ = ECj(fj (i) + Aj (i))

j=1

где обозначено

Aj= jH(i,z)~(z)f(z)dz, Aj = j^dH^i’^z) ~(z)fj(z)dz (20) 0                                 0    ^di

Начальные параметры y₀=y(0), y₀ = y'(0).

Из (20) следует, что при $=0 значения функций Jj($) и Д! ($) обращаются в нуль.

Тогда из (19)

у0=2 Cjf,(0)

■¹=1                 .                        (21)

.j=1

Решением системы у^авнений (21) будет

'

C1 =-Yi У о + Y 2 У 0, C 2 = Y1У 0 + Y 3 У о,             ⁽²²⁾

где обозначено

i

2h⁴(0)

i h'(0)

h²(0)

4 h(0)

, Y 2 =---------г/---------, Y з =

2h⁴(0)

^^^^^^в

h >2(0) +

4 h(0)

2h¹⁴(0)

.

Подставляя (22) в (19), найдем

У = Y1 y0 (- fl - A1 + f2 + A2 ) + Y2 y0 (f1 + A1 + f2 + A 2 )

<'A⁽²³⁾

Г^аничные условия дают возможность получения частотного у^авнения 11

Из фо^мулы (24) вытекает важный ^езультат cos ^(1,0)+ O(k ') = 0.

Этот ^езультат можно существенно улучшить. Нап^име^, можно получить асимптотическое п^едставление с остаточным членом — -2            —-1

O(k ), а не O(k ).

Функция h может быть п^едставлена в виде

h = k m(^),                   (25)

Тогда функции ro(5,0) и g(§) принимают вид

_ 5   1

' (5,0) = kJ m

k

2>

_ 5 m5 )

Вто^ое слагаемое у^авнения (24) с учетом п^едставлений (25) и

(26) можно записать

f- r

L 0

A i

J 0

Рассмот^им т^етье слагаемое у^авнения (24). Введем обозначения

r (5) = ®(1,5)-2®(5,0), r '(5) = -3 km12 (5), r "(5) = - 3 k^L;

²m²²

• ⁶0 m ^л

Таким образом, частотное уравнение (25) можно записать в виде

J r( k) +1J 2( k) +    J 3( k) = 0.               (29)

k k

П^именение к у^авнению (29) тео^емы о нулях функции с известными асимптотическими п^едставлениями позволяет получить асимптотическое вы^ажение для собственных частот п^одольных колебаний:

—*   n(2n -1)

Kn = —-----<

J m12 d5

. 0

^^^^^^e

n²(2 n -1)²

U O

■ (k-2 )• *'

Множитель пе^ед фигу^ной скобкой есть собственная частота соответствующего сте^жня с постоянной жесткостью и плотностью. Пе^вое слагаемое в скобках дает п^иближение метода фазовых интегралов.

Выводы. В работе предложено решение уравнения Вебстера для косинусного излучателя с использованием метода ВКБ. Подобного

^ода излучатели могут быть использованы как т^ансфо^мато^ы импеданса, а также как соединители двух т^уб ^азличного сечения, к^оме того, косинусный излучатель является эффективным фильт^ом высокой п^оходимости. Полученные ^езультаты помимо акустики могут найти п^именение в д^угих областях знаний, нап^име^, в медицинских исследованиях для описания нелинейных пульсовых вол.

Orel State Agrarian University named after N.V.. Parakhin

In the problems of propagation of intense sound, in concentrators and other waveguide systems, an equation of the Webster type arises:

д2р 2 д2р 2dlnS(x) Эр £ д2р2 b д3р dt2 С Эх2 С dx Эх+ с2р dt2 + pdxdt2