Решение в квадратурах расширенного уравнения распространения импульсов в оптических волокнах при произвольной нелинейности

Для огибающей оптического импульса, распространяющегося в одномодовом волоконном световоде, поддерживающем состояние линейной поляризации, выведено [1] уравнение

. (дA о дA^   1 д2A в? д2A i + в,+।

( д z    ¹ д t | 2 в o д z ²    2 д t ²                   (1)

+Ав (| A ²) A = 0, названное расширенным уравнением распространения. Здесь A ( z , t )- комплексная огибающая импульса, to o - несущая частота, в o = ® o n ( ® o )/ c - волновое число, в , = 1/ v g - величина, обратная групповой скорости, в ₂- дисперсия групповой скорости, Ав (| A |²)- нелинейная поправка к постоянной распространения моды в линейном приближении.

В области прозрачности волновода Ав является вещественной функцией.

Это уравнение существенно отличается от общепринятого [2]-[4] уравнения распространения дA „ дA . в2 д2 A      „

+ в1+ i= i (Ав) A д z      д t 2 д t2     1

наличием второй производной по координате. Если в (1) отбросить вторую производную по координате, то получим последнее уравнение.

При известном [2]-[4] выводе этого уравнения отбрасывание второй производной по координате происходит ещё на начальном этапе решения волнового уравнения в спектральном представлении. Это сделано в предположении, что фурье-образ огибающей является медленно меняющейся функцией.

Не считая данную аргументацию убедительной, авторы провели полный вывод [1] уравнения (1) и исследовали его решение в случае керровской нелинейности для кварцевого волокна. Результат получился прямо противоположный - скорее следует отбросить вторую производную по времени.

Грубую сравнительную оценку вклада вторых производных для кварца можно провести в самом уравнении (1), не обращаясь к решению.

Действительно, в области минимальных оптических потерь кварца: % = 1,55 мкм; в2 = -20 пс2/км; n = 1,45, полагая z=ст, получим, что коэффициенты при вто- рых производных различаются на два порядка не в пользу второй производной по времени t.

Для допированных кварцевых волокон с многослойной оболочкой, газонаполненных волокон, полупроводниковых волокон, стёкол, допированных полупроводниками и органическими полимерами, вклад вторых производных может быть сравним.

Целью настоящей работы является точное решение уравнения (1) в квадратурах при произвольной функции нелинейного отклика.

Основной формализм

Функция Ae(|A|2), характеризующая нелинейный от- клик среды на внешнее гармоническое возмущение, принадлежит к одному из трёх классов : конкурирующие, насыщающиеся и переходные нелинейности [5]. Очевидным её свойством является то, что в нуле она обращается в ноль. Керровскую нелинейность можно считать частным случаем конкурирующей нелинейности.

Будем искать решение уравнения (1) в солитонном виде

A ( z , t ) = R ( z , t )exp { ± iqz } ,                           (2)

где R - действительная функция, а q - произвольный неотрицательный параметр, связанный с пиковым значением напряжённости поля.

Подставляя (2) в (1) и приравнивая к нулю мни- мую и вещественную части полученного уравнения, приходим к системе двух уравнений с одной неизвестной функцией:

f, q ) д R 1 д R

I 1 ±— I+

( в o ) д z v д t

1 д ² R -в, д ^; R 2 в o д z ² 2 д t1

± q + ^ -Ав ( R 2 )

R .

Уравнение (3) является линейным однородным уравнением первого порядка.

Как известно из теории таких уравнений, общим решением является любая дифференцируемая функция R = R ( s ( z , t )), где

s ( z , t ) = z - vt ,                                           (5)

v = V g ⁽¹ ± q / ^в o ).                                      ⁽⁶⁾

Таким образом, огибающая представляет собой бегущую волну неизменного профиля, движущуюся с постоянной скоростью (6) (при - q /в 0 =1 возникает стоячая волна).

Профиль этой волны определяется уравнением (4), которое превращается в обыкновенное дифференци-

альное уравнение

f J__ P 2 v ² ) dR ( 2 p o 2 ) ds²

± q + 2^- _д_Р ( R 2 )

R ,

разрешимое в квадратурах. Действительно, умножая

(7) на dR / ds , находим первый интеграл

f -1

12ft

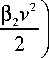
fdR 1 ( ds )

= (± q + q 2/2P o) R2 -

- J ДР ( R 2 ) d ( R 2 ) + C 1

где C ₁ – произвольная постоянная. Обозначая

B ( R 2 ) = J Др ( R 2 ) d ( R ²),                           (9)

разделяя переменные и интегрируя, получим

1 1 -e o p 2 v ² J                 dR                =

V 2 ^е o     ^( ± q + q ² /2 p _o ) R ² - B ( R ²) + C 1    (10)

= z - zo - vt , где в качестве второй произвольной постоянной интегрирования принято (–z0). Формула (10) является общим решением уравнения (7), которое определяется двумя квадратурами. Выполняя интегрирование в (9) и (10), найдём z–z0–vt=f(R,C1).

Обращая данное выражение (если это, конечно, возможно) получим явный вид огибающей R = R ( z – z 0 – vt , C 1 ). Постоянная C 1 определяется поведением огибающей на бесконечности. Отметим, что параметр q по сути является поправкой к волновому числу β ₀ .

Заключение

Таким образом, найдено решение уравнения (1) в виде волнового пакета с неизменным профилем. Формула (10) является основным результатом данной

работы. Решение задачи о распространении оптических импульсов в одномодовых волоконных световодах, поддерживающих состояние линейной поляризации, сводится к вычислению первообразной в левой части (10), что, несомненно, технически проще решения уравнения в частных производных. Даже если эта первообразная не выражается в элементарных функциях, формула (10) определяет общее решение в специальных функциях.