Решение в первом приближении уравнения для давления в газодинамических подшипниках гироскопических приборов

о

(...) = -/(-Ж2;(7)

о

=1  ___2 Т_ХТ₂

(•■■)2=С У = ™ f J( - )AA=(-- )-(8)

о 0

Если оператор осреднения (8) применить к уравнению (4), то получим равенство:

d          Z + ^ ^А + А^хР01г\ + от oqx             oqx            )

+—\d2K0^

Bq_x I 8q_x

^2     8q₂ J

+1— к ₀A| L(a₂-a₁)^(-d^_5i-^+

⁺L^d3kxx~\ ^ot—           ^ot— =°> (3)

ы Al k=i        aq₂j

где

Л$ =Л,+Л2;

Zi = d₂₁X_x + d₂₂X₂;

Z₂ = d_4xX_x + d₄₂X₂ ;

А=А^;

5А

X2=A0^L.

Для нахождения неизвестных функций А) и Х₂ обращаемся к уравнению (3).

Сначала интегрируем его по быстрой переменной ^ частным образом в пределах от начала периода, т.е. от нуля до У Получаем равенство:

А (ад)+^7 (ад) = Ai - Аг - Аз.   (Ю)

где

^ = cZ6cos(p2-Pj);

у =£А .

2 9^’

А1 = А1(91.92<Т А'А) >

Аг = А2(91'9г’т’А'А);

Аз = Аз(91-9г.ТА> А) •

Затем интегрируем уравнение (3) по переменной А частным образом в пределах от нуля до А-Получаем другое равенство:

d^K.Y^d^Y^D^-^    (11)

где

Ai = Aitoi-^.TA A);

Аг = Аг toi. 9г > Т А. А) >

Аз = Аз(91'92'Т> А А) ■

После применения оператора двойного осреднения (...) к уравнениям (10) и (11), получаем систему двух уравнений для нахождения двух неизвестных А А2:

АА + ^?А = Ai - Аг ~ Аз; ^^ toe А + А А = Ai ~ Аг— Аз= где

А1 ~ А1 ;

Ai= Ai ;

Аз =(Л1-Лг)А1А^ +

Аз = (А _ А) A Ato+

+d_nlE^ + d₄₂K^^-. 9%         3q₂

В уравнениях (12) функции D_u = (Onton 9п т, Сд) и Ai = Alton 9i, Т А являются неизвестными.

Для их нахождения, опираясь на результаты исследований опор с одной профилированной по верхностью, будем считать, что если функция Ро не зависит от быстрых переменных и А то функция Рх зависит от быстрых переменных Ci и С? линейно:

Atoi^Mi-AW + ^A+cA- (14)

В этом случае для кусочно-постоянных функций АА и И₂1^ (функций определяющих геометрию прямоугольных канавок на подвижных поверхностях) функции

Аг(91>92'т.АА)= Аг^р^г^-СрСг)= 0;

aZ=aZ=o.                   (15)

Неизвестные функции Ai = Alton 91, г, У и Ai ⁼ Alton 9i, т, А находятся, если снова обратиться к уравнениям (10) и (11), которые предварительно разделить на функцию К_о;

А1) + АА = Т7" А1(91.9г>тА)~

-(X_x-X^d₅₁P₀ — -d_3X^-d_4X^; (16)

V        51 0^   31 ^   41 д^, V / d6Y2+d4Yx = -^-П2Х(ях,9г,т^-

~(А-Aj d₅₂P₀ — -d₃2^--d₄₂-~; (17) А ^9\    9%

Теперь, в силу особенностей уравнений (16) и (17) неизвестные функции Ai ⁼ D_xx(q_x, q_x, т, У и Ai ⁼ Alton 9\, ^т> Ci) находим, применяя к уравнению (16) оператор осреднения (6), а к уравнению (17) - оператор осреднения (7).

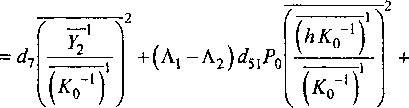
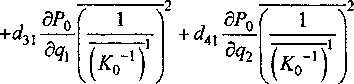
Aitoi.92-TAi) = Aitoi.^.TA)1 =

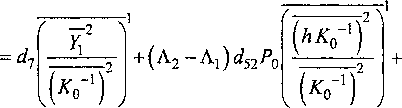
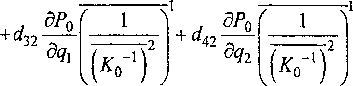
Равенства (18) и (19) после их подстановки в равенство (12), позволяют найти неизвестные Х_х и —2  —1

Х₂, если будут найдены функции Y_x и У₂ .

Решение в первом приближении уравнения для давления в газодинамических...

В соответствии с линейной зависимостью функции Pi = Pi(qb qb т, ^, У от переменных ^ и ^, имеем:

£=И- (21)

Обратившись снова к системе уравнений (16) и (17), подставив в них найденные ранее функции D_n = D_n(q_b q_b т, У и О₂₁ = Ai(^_b q_b т, Q, и применив к уравнению (16) оператор (7), к уравнению (17) оператор (6), получим систему двух уравнений с четырьмя неизвестными и_ь и₂, «з, щ: ^i e(0,«i): d₆n₃ =

Определив неизвестные и_ь и₂, п₃, и₄, находим функции Zi и Z₂:

^1 = ^о[8ц +(At-Л2)т12] + ^)—-х

х(8Х2+т^+Р0^-(5И+т*4у,(26)

'         ' 8q2x '

^2 ⁼^o[^2i +(Ai -Л₂)ти₂₂] + Р₀—2-х

8qx

x(§22 + т23)+Р0 —-f§23 + т2А(27)

v           7      5^2’ и получаем уравнение для главной составляющей давления Р функции Рй\

5 Pyh I л ( ар        ар Л

^ —---+— 4оро“ + А(Л —+ С1(Л + 1                     I 1U U            1U и            1U и

О \                      дРI

+ я  А2йР) "Т5- + В20Р0 Т-2- + С20Р0 = 0.(28)

8q2 V 8qx 8q2)

8Р₀ 9q_x

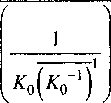
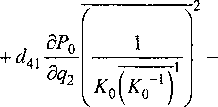
-----^-2

ti e(0,a₂): d₂n_x =

+ (Л₂ - Л]) d₅₂P₀

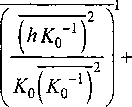
Выражения для функций 5,у, /и,у, т*, А_ю, В_ю, С_т не приводятся, ввиду громоздкости.

Как следует из приведённых рассуждений и выкладок, после подстановки функции Р_о удовлетворяющей уравнению (28) в исходное уравнение для давления, в нем останутся малые слагаемые порядка е³ и менее. Поэтому для числа канавок большем 6, давление Р определяется функцией Р_о с высокой точностью.

В случае профилирования только одной из поверхностей, из уравнения (28) получаются известные уравнения для давления в первом приближении парциальных подшипников [8, 9].

^32^ 8q_x

——-2

+ d 8Р°

+ “42Т--

I 1 г^Р ЙР

-(Л2-AJ^Pg — ~^32 —--^г"^-   (23)

J 8q_x dq₂

Еще два уравнения для нахождения четырех неизвестных щ, и2, и3, и4 получаем, используя равенства:

У =0;

^’ =0.

Отсюда вытекает:

“1 .

и₄ =----- -Из, 1 — OCj

а2

«2 =-;-----«1-1-а2

Заключение

Получено приближенное уравнение для давления в смазочном слое газодинамических опор гироскопов с двумя профилированными спиральными или винтовыми канавками поверхностями деталей подшипника. Оно с высокой точностью заменяет исходное уравнение и не содержит зависимостей давления от быстрых переменных. Полученное уравнение позволяет подойти к его решению и прямыми численными методами, и приближенными методами с целью получения статических и динамических характеристик смазочного слоя, а также изучения динамики роторов гироскопов на таких опорах.