Решение вариационной задачи по выбору оптимальной формы сжатого стержня

Осесимметричные пространственные фермы, составленные из прямолинейных стержней, нашли широкое применение в качестве адаптеров полезной нагрузки. Расчет таких конструкций проводится в предположении, что стержни фермы соединены шарнирно, а основным видом разрушения стержня является потеря устойчивости при действии на него сжимающей силы.

Стержни фермы в большинстве конструкций имеют постоянное по длине поперечное сечение. Однако использование в ферме стержней с переменным поперечным сечением позволяет создавать более эффективные конструкции [1; 2].

Рассмотрим шарнирно опертый стержень длиной l, нагруженный сжимающей силой P. Пусть стержень имеет круглое поперечное сечение, радиус которого r зависит от продольной координаты x. Длина стержня l и его объем V0 являются заданными величинами. Необходимо подобрать закон изменения радиуса поперечного сечения, который обеспечивает максимум критической силы P при известном объеме стержня V0.

Сформулируем условие этой задачи как задачи вариационного исчисления. Объем стержня V 0 определяется функционалом

l

V 0 = J ⁿ [ r ( x ) ] ^ x ^{,                 (1)}

где r ( x ) – зависимость радиуса стержня от продольной координаты.

Уравнение устойчивости стержня имеет вид

Pw

w +———

^xx EJ ( x )

= 0,

где w ( x ) – прогиб стержня; E – модуль упругости; J ( x ) – момент инерции поперечного сечения.

На краях стержня выполняются следующие граничные условия:

w (0) = 0, w (1) = 0.(3)

Момент инерции круглого поперечного сечения будет

π r ( x ) ⁴

J (x)     [4.(4)

Подставляя (4) в (2), получим

[ r (x)] 4 = -     ,(5)

Разделяя переменные и интегрируя уравнение (15) с помощью замены w = u ³, dw = 3 u ² du , найдем общий интеграл уравнения (9):

= 73 Г U ^du + C .

V a ^- u

Выполняя интегрирование в (16), получим общее решение дифференциального уравнения (9):

x = T a

3 w arcsin

a

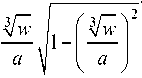
+ c , (17)

где a и C – постоянные краевой задачи, которые находятся из граничных условий (3):

где

2 4 P

=Дт, С =⁰ nJ 3

Подстановка [ r ( x ) ] 2 из (5) и параметра ц из (6) в

Подстановка w xx из соотношения (13) в (5) дает следующее выражение для r ( x ):

функционал (1) дает

V 0 E

2 π P

l

=7

w xx

Объем V 0 в уравнении (7) является постоянным. Поэтому минимум функционала

l

I =Ldx                 (8)

0     w^xx

обеспечивает максимум критической силы P .

Уравнение Эйлера сформулированной вариационной задачи будет следующим:

|                                      |

- wxx J --5“+L--5“ w = 0.         (9)

xx

V   w xx   (V w xx ) xx

С помощью замены

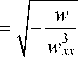
дифференциальное уравнение (9) приводится к виду

( v_vw - vw_v ) = 0.

xxx

Интегрируя уравнение (11) с учетом граничных условий (3) и того, что v (0) = 0, запишем его решение:

- -w- = cw ,              (12)

w xx

где c – постоянная интегрирования. Форма потери устойчивости стержня определяется с точностью до произвольного множителя c , для удобства принятого равным единице:

w = - (13) w xx

Умножим обе части уравнения (13) на 2 w x :

2 w_Tw„ = - 2 w_yw ^{- 1/3}.           (14)

xxx x

Интегрируя уравнение (14), получим

w x = ЛV a ² - w ^2/3 .            (15)

r

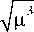
С учетом (18) и (19) общее решение дифференциального уравнения (9) можно записать в виде

l x = —

π

rr arcsin r0r0

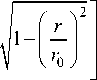
где

. 4 = 16 1 2 P

⁰    3π³ E ^.

На основе решения дифференциального уравнения (20) получено следующее трансцендентное уравнение для определения оптимального закона r ( x ):

arcsin Y-Y \1 -Y 2-n-s = 0,(22)

где rx

Y = —; s = 7.(23)

r0

Для того чтобы уравнение (22) имело вещественные корни, достаточно, чтобы значения параметра s изменялись в следующих пределах:

0 <  s <  0,5.

Численное решение уравнения (22) было выполнено в приложении MATLAB. Для 100 значений параметра s (начальное значение параметра равно 0, шаг изменения параметра = 0,05) из промежутка (24) было найдено значение корня γ (см. таблицу).

Полученные результаты были аппроксимированы методами регрессионного анализа с помощью приложения Curve Expert (рис. 1). Аппроксимирующая функция имеет следующий вид:

Y =

ab + c - s d b + s d

где a = 4,683 938∙10^–3; b = 4,683 938∙10^–3; c = 1,401 818; d = 5,531 215∙10^–1.

Значения корня γ для некоторых значений параметра s

s	0,05	0,10	0,15	0,20	0,25
γ	0,592 751	0,726 609	0,810 933	0,870 672	0,914 770
s	0,30	0,35	0,40	0,45	0,50
γ	0,947 521	0,971 293	0,987 481	0,996 904	1,000 000

Учитывая (23), получим r = Г f (x),

где

f ( x ) =

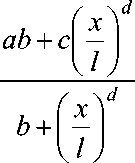
Подставляя (31) в выражение для максимальной критической силы (30), получим

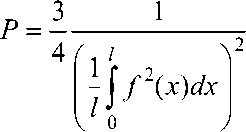
EI П 2      p

— = V P C ,

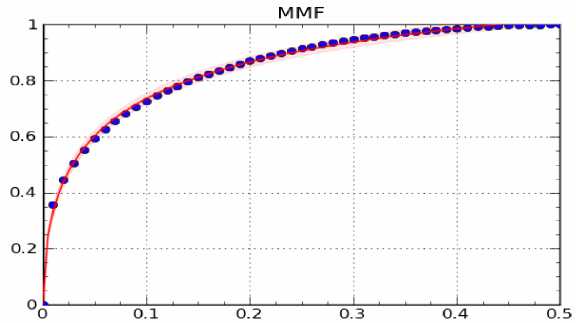
Рис. 1. График аппроксимирующей функции

где P c – максимальная критическая сила для стержня постоянного поперечного сечения.

Интеграл в выражении (32) определялся численно с помощью приложения MATLAB:

l

J f ²( x ) dx = 0,749 292 • l .             (33)

Подставим (33) в (32):

9» 1,36.                   (34)

Подставляя выражение для r ( x ) из (26) в (1), для заданного объема V 0 имеем

r o =

V 0 l

.

ⁿJ f 2 ^{( x})^dx

Из уравнения (21) следует выражение для максимальной критической силы:

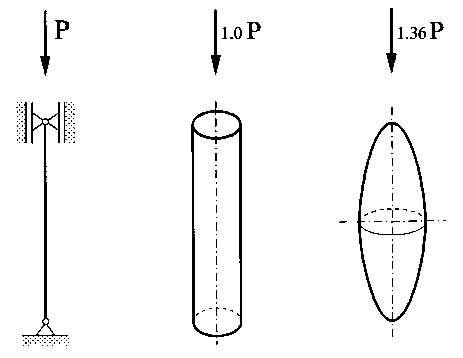
Рис. 2. Сравнение различных форм стержня

P = 3n³ Er L

16 l ²

.

Подставляя (28) в уравнение (29) для максимальной критической силы P , получаем

3π³ E

^P 16 l ²

V 0 ²

.

n J f ²( x ) dx

V 0 J

Так как объем материала постоянный, то

V o = 4 n Il 2 ,

Анализ различных форм стержня показывает, что при заданном объеме V 0 использование переменного поперечного сечения, является оптимальным, повышает на 36 % критическую силу по сравнению с критической силой стержня, имеющего постоянное поперечное сечение (рис. 2).

где I – момент инерции стержня, имеющего постоянное поперечное сечение.