Решение второй основной неосесимметричной задачи теории упругости для анизотропных тел вращения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2025PNRPU MECHANICS BULLETIN

The paper presents a mathematical model for solving the second main problem of the theory of elasticity for limited bodies of revolution made of a transversally isotropic material. Non-axisym-metric kinematic conditions are imposed on the surface of the body, specified according to the cyclic law of sine and cosine. The technique involves the development of the energy method of boundary states, which is based on the concepts of spaces of internal and boundary states, coupled by isomorphism. Isomorphism of state spaces allows us to establish the one-to-one correspondence between the elements of these spaces. The internal state includes the components of the stress tensor, strain tensor and displacement vector. The boundary state includes surface forces and displacements of the body boundary points. Finding an internal state comes down to studying the boundary state isomorphic to it. The basis of the internal states is reduced on the basis of a general solution to the boundary value problem of elastostatics for a transversely isotropic body limited by coaxial surfaces of revolution. Orthogonalization of state spaces is carried out, where the internal energy of elastic deformation is used as scalar products in the space of internal states; in the space of boundary states, the work of surface forces on the displacements of points on the boundary of the body is used. Finally, finding the desired state comes down to solving an infinite system of linear algebraic equations with respect to the Fourier coefficients.

A solution to the second main problem is presented with boundary conditions simulating transverse expansion (without longitudinal compression) for a circular cylinder made of transversely isotropic large dark gray siltstone. The solution is analytical; the characteristics of the stress-strain state have a polynomial form. Explicit and indirect signs of convergence of the problem solution and graphical visualization of the results are presented.

Современные материалы, применяемые в авиакосмической отрасли, в машиностроении обладают асимметрией упругих свойств для разных направлений, т.е. с точки зрения теории упругости являются анизотропными. Это свойство усложняет расчет их напряженно-деформированного состояния. Кроме того, в процессе работы эти тела пребывают в условиях сложного кинематического взаимодействия с другими телами. Естественно, что условия взаимодействия этих тел не являются симметричными относительно, например, оси вращения цилиндрического тела или какой-либо его поверхности. Исследование напряженно-деформированного состояния, возникающего в теле, которое носит несимметричный характер, является актуальной научной задачей для анизотропных тел.

В области решения краевых задач теории упругости для трансверсально-изотропных тел имеется существенный задел. На сегодняшний момент исследуются частные аспекты данных задач для усложненных по геометрии и структуре материалов, например многосвязные, слоистые, нелинейные и др. Например, в работе [1] получены точные аналитические решения задач о равновесии полых и составных транстропных сфер, находящихся под действием внешнего или внутреннего давления. В работе [2] рассмотрена задача о деформации трансверсально-изотропного цилиндрического слоя под действием нормального давления. Полученные асимптотические формулы позволяют описать поведение слоя с разными жесткостями в трансверсальном и тангенциальном направлениях. В работе [3] с помощью преобразования Фурье решена смешанная краевая задача Дирихле – Неймана для уравнения Пуассона в области, ограниченной двумя параллельными гиперплоскостями. Решение записывается через построенную функцию Грина оператора Лапласа. В работе [4] предлагается подход к определению трехмерного напряженно-деформированного состояния (НДС) многослойного транстропного полупространства в случае воздействия на него нормальной нагрузки. Работа [5] посвящена решению контактной задачи для транстропного полупространства с неизвестной областью контакта. Задача сведена к интегральному уравнению относительно давления в зоне контакта, для решения которого применяется численный метод Галанова. В работе [6] методом асимптотического интегрирования уравнений теории упругости рассмотрены осесимметричные краевые задачи для конической оболочки из неоднородного трансверсально-изотропного материала.

В исследовании [7] представлены доказательства теорем о существовании и единственности решения упругопластической краевой задачи, основанной на теории пластического течения трансверсально-изотропных тел. В работе [8] с использованием прямой формулировки метода граничных состояний были решены краевые задачи трехмерной анизотропной теории упругости, сопровождающиеся числовыми примерами для нескольких типов анизотропии. В работе [9] анализировалось предельное нагружение конструкций, выполненных из трансверсально-изотропных материалов, в условиях кусочно-линейной текучести. В работе [10] исследовалась трехмерная задача деформирования трансверсально-изотропного слоя, находящегося под действием нормального давления. Получены асимптотические решения для слоя с сильным отличием жесткостей в трансверсальном и тангенциальном направлениях. В работе [11], используя преобразование Фурье, приводится решение пространственной задачи о действии нормальной нагрузки на неограниченное слоистое трансверсально-изотропное основание. Работа [12] посвящена построению уточненной итерационной теории построения напряженно-деформированного состояния трансверсально-изотропных балок. Теория описывает как внутреннее состояние, так и краевые эффекты типа пограничного слоя. В работе [13] строится напряженно-деформированное состояние трансверсально-изотропных сферических и эллиптических оболочек, находящихся под действием внутреннего давления. Построению фундаментального решения уравнений статики для трансверсально-изотропных пластин посвящена работа [14]. Пластины находятся под действием сосредоточенной силы. Исследовано влияние упругих констант на влияние на напряженно-деформированное состояние пластин.

В работе [15] исследовалась динамическая задача для трансверсально-изотропного слоя малой толщины. Получены асимптотические разложения однородных решений, позволяющие рассчитать напряженно-деформированное состояние при различных значениях частоты вынуждающих нагрузок. Исследованию задачи устойчивости трансверсально-изотропных оболочек под действием динамического давления посвящена работа [16], где строится полная система решений уравнения движения сферической оболочки и определяются формы потери устойчивости, а также частоты собственных колебаний.

На сегодняшний момент для трансверсально-изотропных тел вращения средствами метода граничных состояний решена первая основная задача теории упругости при наличии массовых сил [17]. Решению второй основной задачи при одновременном действии на тело массовых сил посвящена работа [18]. По идентичной методике, что и во второй основной задаче, решены основная смешанная [19] и контактная [20] задачи. Особенность решения данных задач заключатся в том, что полученное упругое поле в каждой задаче является осесимметричным и удовлетворяет одновременно заданным условиям как на поверхности тела, так и внутри области (массовым силам). В области неосесимметричных краевых задач механики решены первая [21; 22] и основная смешанная [23] задачи теории упругости.

Целью данной работы является решение неосесимметричной второй основной задачи теории упругости для трансверсально-изотропного тела вращения.

Постановка задачи

Рассматривается упругое равновесие трансверсально-изотропного конечного и односвязного тела вращения с осью анизотропии, совпадающей с геометричес-

кой осью симметрии. Требуется определить напряженно-деформированное состояние, возникающее в теле, по заданным на границе перемещениям u = { u _r , u _θ , u _z } (рис. 1). Тело занимает область V .

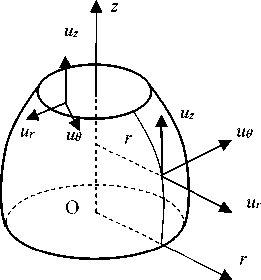
Рис. 1. Трансверсально-изотропное тело вращения

Fig. 1. The transversely isotropic body of revolution

Перемещения точек границы изменяются по циклическому закону (синуса или косинуса). Объемные силы отсутствуют.

Определяющие соотношения для среды

Решение задачи строится в цилиндрической системе координат r , θ, z _. Для однородной трансверсально-изотропной среды имеют место следующие соотношения.

Дифференциальные уравнения равновесия [24]:

∂τzr   ∂σr 1 ∂τrθ   σr- σθ

++   +    =0;

∂ z ∂ rr ∂θ r

∂σ ∂τ 1 ∂τ τ z+zr+zθ +zr=0 ; ∂z∂rr∂θr

^∂τ z θ ₊^∂τ r θ ₊ 1 ^∂σ θ ₊ 2 ^τ r θ₌ 0 ∂ z ∂ rr ∂θ ^,

Соотношения Коши [24]:

∂ w

εz =     ;

∂ z

∂ u

εr =     ;

∂ r

εθ

r

1 ∂ vu

+ ; r ∂θ r

∂ w ∂ u

γzr =    +    ; γrθ =

∂ r ∂ z

1 ∂ u ∂ v +

r∂θ ∂r

-

v

; γ _{z θ} = r

∂ v

1 ∂ w

+ ∂zr∂θ

.

Уравнения совместности деформаций [25]:

1 ∂ ( r 2 ∂ε θ ) ₊ 1 ∂ ² ε rr _- 1 ∂ε r r ² ∂ r ∂ rr ² ∂θ ² r ∂ r

1∂∂εzθ1∂2εrθ (r)+ r2∂r∂θr∂θ∂z

-

-

^{2 ∂} ( r ^{∂ε r θ} ) = 0; r ² ∂ r ∂θ

-

^{1 ∂ 2 ε zr} - ^{1 ∂} ( r ^∂εθθ ) + ^{1 ∂ε rr} = 0;

r ² ∂θ ² r ∂ r ∂ zr ∂ z

^∂ ( ^{1 ∂ ( r ε z θ )} ) + ^{1 ∂} ( r ^{2 ∂ε r θ} ) +^∂ ( ^{1 ∂ε zr} ) ∂ rr ∂ r r ² ∂ r ∂ z ∂ rr ∂θ

-

^{1 ∂ ε rr} = 0; (3) r ∂θ∂ z

1 d2s 1 Sz    d2eflfl 2 d4fl 2 dz     n zz zz θθ zθ zr

—;--1— +----1-- Z -------= 0

r ² d0 ²    r d r     d z ²    r d0d z r d z

1     + r 2 (1 Ч0) -d^-Ч (1 dz z ,) = 0

r 60S z    д r r д z     д z ² д r r 50

₊ дЧ - ₂ д £ zr д z ²     д r ²      д r д z

Обобщенный закон Гука [26]:

^£ z = у [ ° z ^-V z ( ° r +^ 0 ) ] ; E_z

£ r =—(° r-V r °0)- -° ° z;

EE

£0 =

Er

^-V r ° r ) ^-

^V z ° z ;

E z

^γ zr ^{= τ} zr G_z

G r ^τ

; y z 0 =—^T z 0 ; y r 0 =

Gz

■ - 2(1 +v r ) _T

' r 0           ^         ^T r 0 •

Er

Здесь: u , v , w - компоненты вектора перемещений u вдоль оси r , 0, z соответственно; £ _r , £ ₀ , £ _z , Y _{r 0} , Y z ₀ , Y _zr - компоненты тензора деформаций; ° _r , °₀ , ° _z , т _{r 0} , т z ₀ , т _zr - компоненты тензора напряжений; E_z и E_r -модули упругости соответственно в направлении оси z и в плоскости изотропии; V _z - коэффициент Пуассона, характеризующий сжатие вдоль оси r при растяжении вдоль оси z ; V _r - коэффициент Пуассона, характеризующий поперечное сжатие в плоскости изотропии при растяжении в этой же плоскости; G_r и G_z - модули сдвига в плоскости изотропии и перпендикулярной к ней.

Метод решения

Для решения задачи используется метод граничных состояний (МГС) [27]. Основу метода составляют пространства внутренних Н и граничных Г состояний:

^Н = {4Ч Ч-,^ k »— } ; Г = { Y 1 , Y 2 , Y 3 ,-, Y k ,... } . (5)

Внутреннее состояние определяется наборами компонент вектора перемещений, теноров деформаций и напряжений (индекс k в правой части помещен наверх):

^ k = { U k , £ kj , ° k }.

Граничное состояние y j определяется наборами компонент вектора перемещения точек границы u v = u_vi , поверхностными усилиями p v = p i :

Y k = ^{{ и} Ч P^{j }}, P k =° j n j , ⁽⁶⁾ где n j - компонента нормали к границе.

Воспользуемся при построении решения основных задач механики уравнением Клапейрона при отсутствии объемных сил [11], [28]:

J p v u v dS = J ° j ^£ ij dV .                 ⁽⁷⁾

SV

На основе равенства (7), можно назначить скалярные произведения в пространствах состояний. Скалярное произведение в пространстве внутренних состояний выражает внутреннюю энергию упругого деформирования (например, для 1-го и 2-го внутреннего состояний):

(Ч^) = J ( z j ° 2 + £ 2 ° j ) dV ,            (8)

V причем в силу коммутативности состояний среды:

(Ч^) = (Ч4 = J ^£ ‘ ° j dV = J z j ° j dV .

VV

В пространстве граничных состояний Г согласно (7) скалярное произведение выражает работу внешних сил по поверхности тела S (например, для 1-го и 2-го внутреннего состояний):

⁽ Y 1, Y 2) = J P i ^{1 U}v^dS .

S причем в силу тождества Бетти и соотношения Клапейрона: (Y1, Y2) = (Y2, Y1).

В случае гладкой границы и в силу (7) оба пространства состояний являются гильбертовыми и сопряжены изоморфизмом. По определению, каждому элементу ^ _k е н соответствует единственный элемент y _k е Г , причем это соответствие взаимно-однозначное: ^ k о Y k . Это позволяет отыскание внутреннего состояния свести к построению изоморфного ему граничного состояния.

После построения базисов пространств внутренних и граничных состояний, необходимо провести их ортонормирование. Ортонормирование базиса пространства Н осуществляется по разработанному рекурсивно-матричному алгоритму ортогонализации [29], где в качестве перекрестных скалярных произведений принимается (8). Алгоритм основан на процессе Грама - Шмидта, переписанном в форме, использующей лишь перекрестные скалярные произведения элементов исходного базиса, которые сведены в матрицу Грама. Если в процессе ортогонализации на k -м шаге встречается некоторый элемент базиса внутренних состояний ^ _k , алгоритм на этом шаге выдаст «0» (нулевое), если этот элемент является линейной комбинацией элементов ^ 1 , ..., ^ _k - 1 . Для сохранения ортогональности выходных элементов и для предотвращения деления на ноль при ортонормировании алгоритм делает проверку на нулевые элементы и исключает их. На их место идут следующие элементы исходного базиса внутренних состояний и процесс повторяется.

Ортонормированный базис Г редуцируется из орто-нормированного базиса внутренних состояний, используя выражения (6) и (1).

Окончательно проблема сводится к разрешающей системе уравнений относительно коэффициентов Фурье, разложения искомых внутреннего ξ и граничного γ состояний в ряд по элементам ортонормированного базиса: ∞∞ ξ = ∑ c_k ξ _k ; γ = ∑ c_k γ _k k = 1                  k = 1

или в развернутом виде:

^∞∞ ∞ ^∞ p_i = ∑ c_kp_i^k ; u_i = ∑ c_ku_i^k ; σ _ij = ∑ c_k σ _i ^k _j ; ε _ij = ∑ c_k ε _i ^k _j .(9) k = 1                     k = 1                     k = 1                     k = 1

В случае второй основной задачи коэффициенты Фурье представляют собой скалярное произведение:

c_k = ∫ p _v ^j u _vdS ,                   (10)

S где pvj – базисные поверхностные усилия в пространстве граничных состояний.

Тестирование коэффициентов Фурье осуществляется подстановкой одного из базисных элементов с соответствующими перемещениями точек границы тела в качестве заданного, при этом должны выполняться условия c_n = 1 , n – номер тестируемого элемента, остальные коэффициенты Фурье должны равняться нулю.

Формирование базиса

Основную сложность формирования решения в МГС является конструирование базиса внутренних состояний, который опирается на общее или фундаментальное решение для среды; также возможно использование каких-либо частных или специальных решений.

В работе [24] с помощью метода интегральных наложений установлена зависимость между пространственным напряженным и деформированным состоянием упругого трансверсально-изотропного конечного тела без полостей и определенными вспомогательными двумерными состояниями, компоненты которого зависят от двух координат z и y (переменных).

При установлении зависимости используется следующий прием. Упругое тело, напряженное состояние которого требуется изучить, рассматривается как часть некоторого бесконечного цилиндра с осью η , параллельной образующей цилиндра. С телом связана система координат rθ z. Меридианное сечение тела совпадает с плоскостью поперечного сечения бесконечного цилиндра с осями координат zy (направление η ⊥ плоскости zy, ось z общая для тела и цилиндра). Предполагается, что цилиндр находится в некотором двумерном напряженном состоянии, не меняющимся вдоль образующей. Компоненты этого состояния upl , upl , upl , σpl , σpl , σpl , σpl y η      z      y z zy η определяют плоскую деформацию с депланацией сечения цилиндра в плоскости zy. Эти же компоненты определяют напряженное состояние заданного упругого тела, так как оно является частью цилиндра. Для определения пространственного напряженного состояния тела рассматривается ряд цилиндров, отличающихся направлением образующей, или углом поворота относительно оси z. Представляя последовательно тело вырезанным из каждого такого цилиндра при m →∞ (m – число цилиндров), редуцируется ряд напряженных состояний, суперпозиция которых и дает суммарное трехмерное состояние. В общем случае напряженное состояние каждого цилиндра в процессе поворота изменяется, и трехмерное состояние тела будет неосесимметричным (зависящим от угловой координаты θ ). Например, для компоненты вектора перемещения w пространственного состояния имеет место выражение:

m w= 1 ∑(uzpl)k .

m k = 1

Перейдя к пределу при m →∞ , сумма заменяется интегралом. При последующей замене переменой интегрирования окончательно связь между перемещениями неосесимметричной деформации и плоской деформации соответствующего цилиндра имеет вид [24]:

b u=∑[uncosnθ+unsinnθ]; n=a

b v=∑[-vnsinnθ+vncosnθ];          (11)

n = a

b w=∑[wncosnθ+wnsinnθ];

un

vn

ππ

∫ ( u_y ^pl + u _η ^pl )cos( n - 1) β d β+ ∫ ( u_y ^pl 0 2 π 0

- u _η ^pl )cos( n + 1) β d β;

ππ

( u y ^pl + u η ^pl )cos( n - 1) β d β- ¹( u y ^pl

02π0

- u _η ^pl )cos( n + 1) β d β ;

1π wn=    uzpl cos nβdβ,

π 0

где a и b – пределы суммирования.

Соответственно для компонент тензора напряжений имеют место следующие выражения:

σ z

σ r

σθ

b

= ∑ [ σ nz cos n θ + σ nz sin n θ ];

b

= ∑ [ σ ny cos n θ + σ ny sin n θ ];

b

= ∑ [ σ n _η cos n θ + σ n _η sin n θ ];

n = а

b

σ _zr = ∑ [ σ ⁿ _zy cos n θ + σ ⁿ _zy sin n θ ];

b

σ _{r θ}= ∑ [ σ ⁿ _{y η} cos n θ-σ ⁿ _{y η} sin n θ ];

b

° z e = E [ ° n n cos n °-° n n sin ⁿ ° ];

n = a

S 1 = I f CT pl cos n p d P ; S 2 = — f ( ст pl + ° ^pl )cos n p d p ;

ⁿ 0                    ⁿ 0

S 3 = - ( ° Pl - < + ^{2 ст} P n ) cos( n - 2) P d в ;

ⁿ 0

S 4 = - J ( ° pl - ° p ^l - 2 ° y ' ) cos( n + 2) P d в ;

ⁿ 0

s 5 = -J ( ° i+° ^)cos( n - 1) P d P ;

ⁿ 0

s 6 = -J ( ° pl -° P 0 )cos( n + 1) P d P ;

^П 0

° z = S - ; ° n = (2 S 2 + S 3 + S 4 )/4; °; = ( S 5 + S б )/2;

° n = (2 S 2 + S 3 + S 4 )/4; ° n „ = ( S 5 - S J/2;

° y n = ( S 3 - S 4 )/4.

Здесь компоненты с верхним индексом pl соответствуют компонентам плоского вспомогательного состояния.

В качестве плоских вспомогательных состояний используется плоская деформация и депланация, возникающие в сечениях цилиндра, имеющего в каждой точке плоскость упругой симметрии, параллельную плоскости zy (направление n 1 плоскости zy ) [24]:

можно сгенерировать набор плоских вспомогательных состояний (13) и по зависимостям (11) и (12) построить совокупность пространственных состояний, образуя базис пространства внутренних состояний (5).

Решение задач

Рассмотрим упругое равновесие трансверсальноизотропного кругового в плане цилиндра из горной породы – алевролит крупный [28]. После процедуры обез-размеривания параметров задачи, аналогия которой приведена в работе [30], упругие характеристики материала составили: E_z = 6,2i; E r = 5,68; G_z = 2,55; v _z = 0,22; v r = 0,24, и цилиндр занимает область V = {( z , г )| 0 <  г <  i, - i <  z <  i}.

Область цилиндра и граничные условия представлены на рис. 2.

u_y^pl = ^Re[ iq — Q x ( ^ i ) + iq 2 Ф 2 ( 5 2 ) ^];

U z^pl = ^Re[ P i Q i 4 ) + p 2 Ф 2 fe ) ^]; ° ^pl = ^{- Re[} Y 2 Q 1 ( ? i ) ⁺ У 2 Ф 2 ( ^ 2 ) ^];

Рис. 2. Граничные условия к задаче для цилиндра

Fig. 2. Boundary conditions to the problem for a cylinder

° y^pl = ^Re[ ф i 4 ) ⁺q 2 ( ^ 2 ) ^];            (13)

° zypl =- Re[УiФi (?i )+ъф2 (^2)];

° z n ^pl = ^Re[ i у 3 Ф 3 ( ^ 3 ) ^]; ° y n ^pl = ^{- Re[} Ф з ( ^ 3 ) ^];

E plpl    r pl n Гг^у z E zz ,

где константы q i , p i и у ₃ определены упругими параметрами материала; 5 j = z / у j + iy ; y _i и у ₂ - комплексные корни характеристического уравнения [9]; функции Ф j ( 5 j ) - аналитические по своим переменным.

Придавая функциям ф j ( 5 j ) поочередно значения:

Ч Ч)'

Ф2(?2) чФэ Ч 7

к

' 0 '

m

к0 J

' 0 '

m к⁵ 3 7

' i 5 i '

к 7

f 0 Л i 5 m к ⁰ 7

f0 Л

m

к i5 7

m е N ,

Особенности формирования базиса в зависимости от вида заданных граничных условий описаны в работах [21; 23].

Базис внутренних состояний формируется из левых частей выражений (11) и (12) с пределами суммирования a = 2 и b = 2 , например, для перемещений:

bb u = EH Un cos( n °)]; v = E [-Vn sin( n °)];

n = a                           n = a

b w = E[wn cos(n°)] . n=а

После процедуры ортонормирования и исключения линейно-зависимых элементов, базисный набор для компонент вектора перемещения представлен в таблице (показано 6 элементов). В таблице истинное значение показанной величины равно показанному значению, умноженному на коэффициент к .

При решении задачи использовался базис из 71 элемента. Приведем значения для восьми коэффициентов Фурье (10):

S 1

u| _{S i} = {sin2 ° ,0,0}, S J г = 0, - i < z < i;

u| _S 2 = { г sin2 ° ,0,0}, S ₂1 z = - i, 0 <  г <  i;

ⁱ-^ u| _S 3 = { г 3sin2 e ,0,0}, S ₃| z = i, 0 <  г <  i;

S 2

с 1 = 3,7934; с 2 =- 0,1838; с ₃ =- 0,1478; с ₄ =- 2,0768;

с 5 = 4,0221; с ₆ = - 0,3465 ; с ₇ = 0,2602; с ₈ = 0,093.

На рис. 3 представлен график, иллюстрирующий «насыщение» суммы Бесселя (левая часть неравенства Бесселя). Это является косвенным признаком сходимости решения.

Перемещения ортонормированного базиса ( к = 10 - ³)

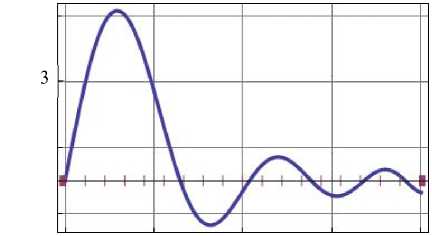
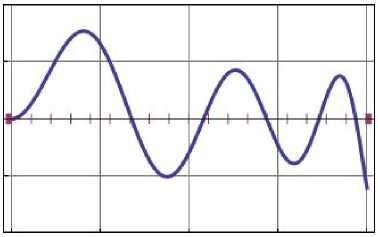
граничными условиями в результате решения (рис. 4). Здесь и далее на графиках заданные () и восстановленные () ГУ изображены в масштабе: истинное значение величины равно указанному значению на графике, умноженному на коэффициент к . С целью визуального выявления максимальной погрешности угол 0 выбран таким образом, чтобы тригонометрические функции имели максимальные значения.

Displacements of an orthonormal basis ( к = 10 ³)

u	v	w
131 r sin2 0	131 r cos2 0	0
143 rz sin 2 0	143 rz cos2 0	66 r 2 sin2 0
- 178 rz sin 2 0	- 178 rz cos2 0	200 r 2 sin 2 0
- (8 r + 47 r 3 - 132 rz 2)sin	- (8 r + 23 r 3 - 132 rz 2)sin	132 r 2 z sin2 (
(11 r + 6 r 3 - 266 rz 2 )sin2	(11 r + 147 r 3 - 266 rz 2)sin	251 r 2 z sin2
(185 r - 52 r 3 - 14 rz 2)sin	(185 r - 225 r 3 - 14 rz 2)sin	137 r 2 z sin2 1

0.5

0.4

0.3

0.2

0.1

N

0 10 20 30 40 50 60 70

Искомые характеристики упругого поля определяются по зависимостям (9).

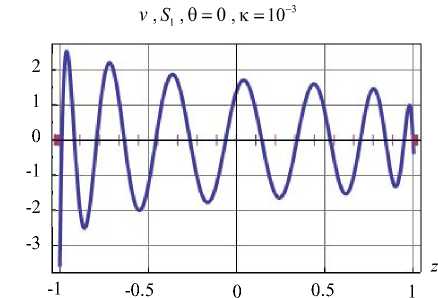
Проверка результата и оценка точности осуществляется сопоставлением заданных ГУ с восстановленными

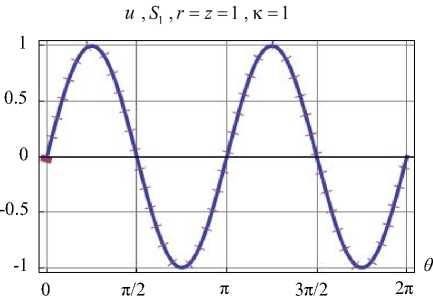
Рис. 3. Сумма Бесселя

Fig. 3. Bessel sum

-2

-4

-6

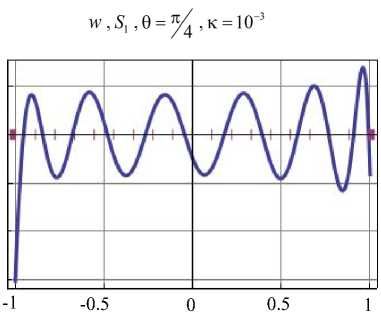
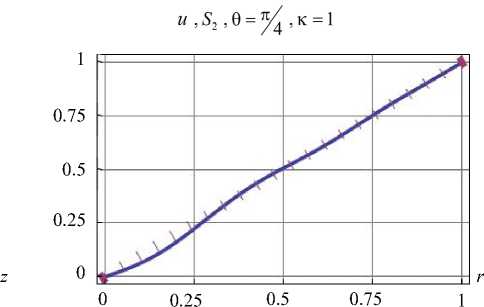
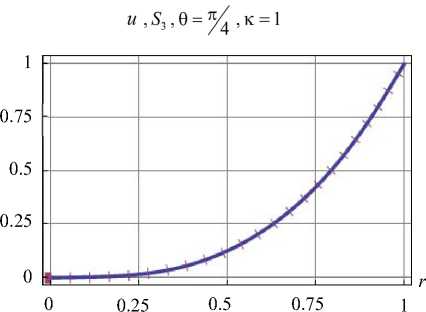
Рис. 4. Верификация граничных условий на участках поверхности

Fig. 4. Verification of boundary conditions on surface areas

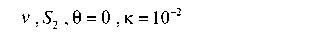
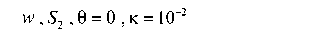
-1

0.5

0.75

0.25

r

-5

r

0.5

0.75

0.25

-10

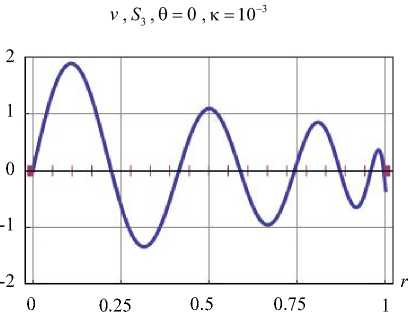
w ,,0=% , к = 10

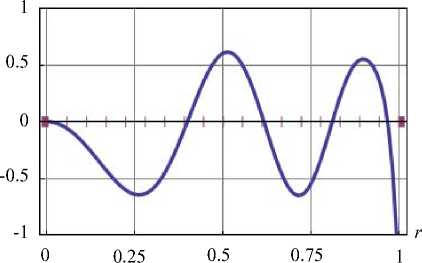
Рис. 4. Окончание

Fig. 4. The end

Характеристики полученного напряженно-деформированного состояния представлены в виде изолиний на рис. 5 (в явном виде необозримы). Истинное значение показанной величины равно соответствующему значению на изолиниях, умноженному на коэффициент κ . На изолиниях рис. 5, а , показана область 0 ≤ r ≤ 1, - 1 ≤ z ≤ 1. На рис. 5, b , показаны изолинии компонент тензора напряжений в зависимости от угловой координаты θ . Приведено сечение z = 1 .

σ_θ , θ=^π 4 , κ= 1, σ _{r θ} , θ= 0, κ= 1 σ _rr , θ=^π 4, κ= 1

Полученные компоненты упругого поля удовлетворяют всем уравнениям теории упругости для трансверсально-изотропного тела (1)–(4).

Таким образом, в работе сформулирована методика решения неосесимметричной второй основной задачи теории упругости для трансверсально-изотропных тел вращения в случае, когда перемещения точек границы заданы по циклическому закону. Методика представляет собой развитие метода граничных состояний, а именно представлен новый способ формирования базиса внутренних состояний, основанный на общем решении задачи о плоской деформации. Исследован прием декомпозиции базиса под условия конкретной задачи.

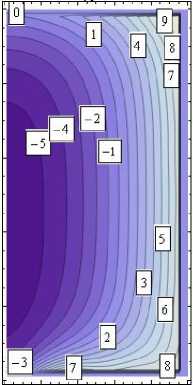
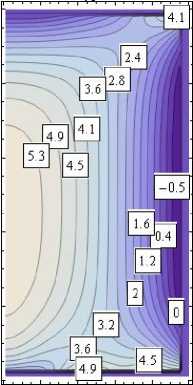
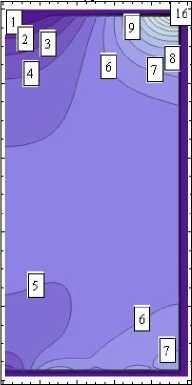
σ

rz

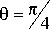
κ = 10 ^{- 1}

σ _zz , θ= 0 , κ= 1

σ _{z θ} , θ= 0 , κ= 1

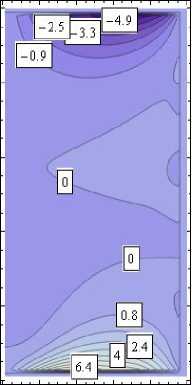
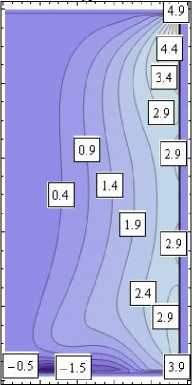
v , θ=^π 4, κ= 1        w , θ=^π 4 , κ = 10 ^{- 3}

u , θ=^π 4, κ= 1

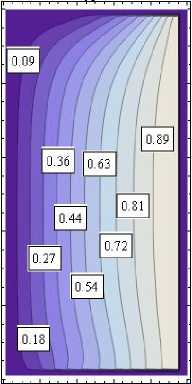
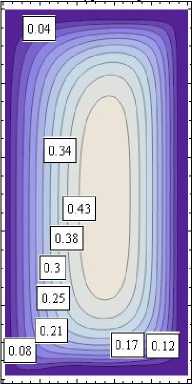
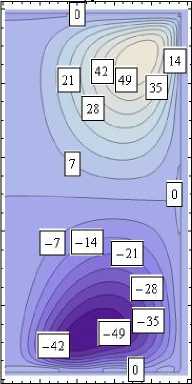
а

Рис. 5. Изолинии компонент полученного упругого поля: а – в меридиональных сечениях цилиндра; b – в поперечном сечении цилиндра

Fig. 5. Isolines of the components of the resulting elastic field: a – in the meridional sections of the cylinder; b – in the cross-section of the cylinder

σ_θ , κ= 1

σ _{r θ} , κ= 1

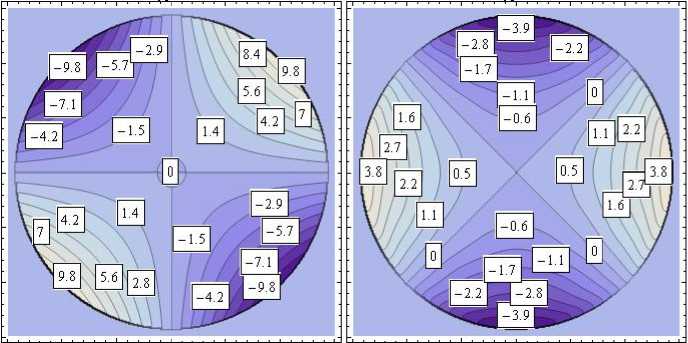
σ _rr , κ= 1

σ _zz , κ= 1

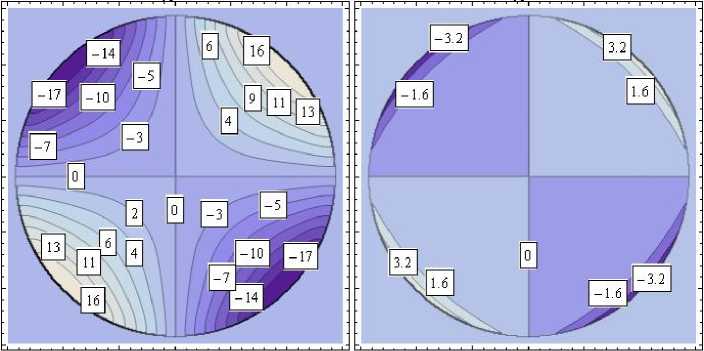
σ _{z θ} , κ= 1

σ _zr , κ= 1

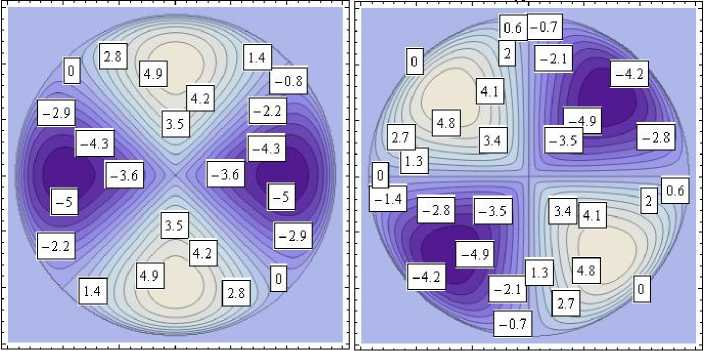
b

Рис. 5. Окончание

Fig. 5. The end

Предложенная методика, однако, не является общей для любого класса рассматриваемых областей (односвязных и многосвязных). В случае многосвязных областей представления (15) для комплексных потенциалов будут иными. Скорость сходимости рядов зависит от граничных условий и условий внутри области, а также от геометрии тела.

Решение является аналитическим и имеет полиномиальный вид, что позволяет легко проводить анализ полученных характеристик напряженно-деформированного состояния.