Решение задач газовой динамики разрывным методом Галёркина в криволинейной системе координат

Введение. Численные методы повышенного порядка точности для решения задач механики сплошной среды на сегодняшних день развиваются многими научными коллективами [1–4]. Наиболее перспективным методом является метод Галёркина с разрывными базисными функциями [5]. Он сочетает в себе качества конечно-объемных и конечно-элементных методов, что позволяет получать с достаточной точностью решать задачи, решения которых характеризуются высокими значениями градиентов. В данной работе построена методика решения одномерных задач газовой динамики, обладающих сферической симметрией. Выполнены тестовые расчеты для задачи о сильном точечном взрыве [6; 7].

Разрывный метод Галёркина. Определим разрывный метод Галёркина [5] для одномерной неоднородной системы уравнений Эйлера.

dq   1 d(rⁿf)

dt  rn dr

+ h — 0,

где

ЧрЭ

/ ри\ f = 1ри2+р);

\ риН/

В приведенных выше уравнениях ρ – плотность жидкости, u – скорость жидкости, p – статическое давление, E и H – полная энергия и полная энтальпия на единицу массы.

ри2

р (Y-1)+

Н = Е+ -. Р

Для нахождения давления используем уравнение состояния идеального газа

Р = (у- Ург,                                 (7)

где у - показатель адиабаты.

В уравнениях (1) – (4) n = 0 для декартовых координат, n = 1 для цилиндрических координат и n = 2 для сферических координат.

Для применения разрывного метода Галеркина введем равномерную сетку

0 < r i < ... < г._ 1 < г. 1 < — <  rN_i <  1. 2               2       "2                 2	(8)
На каждом отрезке определим базис
P ok (t) = 1,	(9)
г — г
Plk(t) =  Дг '	(10)
/ г — гг\2 Р2М = ( Дг ) '	(11)
Аг = г. i — г._ 1 . + 2        2	(12)
Приближенное решение qh в каждой ячейке  [г._ 1 , г.+ 1 ]представляется	в виде
разложения по базисным функциям (9) – (12).

C dq             f 1 d(rnf)             Г h^k(r)dK = 0,

J -^(r)dK + J rn^—^(r)dK + J к              к                    к где dK = rndr - для одномерного потока.

Для одного пространственного измерения уравнение (14) принимает вид

Г.  1

i+2

г dq

J ^Ф) ⁽r⁾ⁿdr + [frⁿy_k (r^)] i+1

г.  1

^i- 2

[frⁿ^_k(r^)] i-i

—

—

Г.1

i+2

J f ^d^ rⁿdr + J h^_k(r)rⁿdr = 0.

Г. 1Г. 1

i-2

Функция f не определена в точках r._1 и r. 1 - решение может быть разрывным на 2        + 2

гранях элементов, что приведет к неоднозначности. Эта проблема преодолевается с

помощью соответствующего выбора численных потоков на гранях, зависящих от предельных значений функции qh слева и справа от точек r._1 и r.+1. 2      +2 Будем использовать дискретные потоки Русанова-Лакса-Фридрихса. flti = f(q+,q+) = 2        2     2      2' : 2(f( + f(qL+1) — a(q*1_ — qL+1)\               (16) T2           ~2      ~2 а = max{ q- 2 + CL, q + 2 + C*}.   c=||                 (17) Используя приближение для функции qh, получим систему дифференциальных уравнений

dq ~77 = dt

: " ' (frn&)\  —/ ^d-r^+l hr^dr ■    (18) _                   Г +1     l—                           i- 2                   _

Ограничители наклона. Для многих конечно-разностных или конечно-объемных вычислений характерны разрывные решения и возникновение осцилляции. Так же и в нашем случае, вблизи разрывов потока могут возникать ложные колебания, поэтому необходимо использование лимитеров. Одним из общих подходов к решению данной проблемы служат специальные ограничители.

Согласно [5] будем обозначать действие оператора лимитирования на функцию q следующим образом: An_hq. Одним из простых подходов ограничения служит лимитер Кокбурна.

Запишем разложение решения по линейному базису в ячейке:

r — rc q = q0 + qi^r~’

Ar =

r-Л +

-

r

i

i

Для функции (19) действие оператора ЛП_hq запишем как

__r — rc nnhq(r, t) = q0+ qi -^—,    Ar = r^ - r.^ .

Значение функции q₁ вычисляется как

q i = 2* minmod [q (r^ - q 0i , a (q^ - q^, a (q_O i - q — )] ,

где q_O i - среднее значение на интервале r._i,r. i , а q 2       2

.1 и q._ i равны 2          2

q i+ i =

q oi+i + q oi

’

4 =

^q oi-i ^{+ q} oi

.

Если порядок полинома больше 1, то

1           I      I r -rc ql(r,t) = ql0 + qi—^,

Ar =

^ri + 1^-ri-1 ’

$ 2

где q ^ = q₀ + ---среднее интегральное значение на интервале r. i ,r. i для полинома

-    -   ¹²                                                   i~- ⁱ⁺ 2

степени равной 2.

После применения лимитера ,             )       ) r - r_c

Aⁿ_hq^l(r, ^t) = ^q 0 + ^qi-^-’    ^Ar = ^r_i+ i ^{- r} _i- l .                  (24)

Постановка задачи Седова о сильном точечном взрыве [6]. Поместим небольшое количество безразмерной энергии г = 1 в небольшую область радиуса dr в центре сетки, заполненной неподвижной средой плотности р0, с давлением р0. Безразмерное давление внутри этого объема определяется:

=  3(у-1)г х < Хе,

^Ро   (у + 1)udr^v ’

Р о = 10 ⁵, Х > Х е ,                                    (26)

где v = 2 для цилиндрических координат, v = 3 для сферических координат.

Выбираем dr в 3,5 раза больше, чем шаг сетки. Плотность устанавливается равной р₀ = 1 по всей сетке, скорость изначально в покое и₀ = 0.

На рисунке 1 представлены результаты расчетов, масштабированные относительно значений на фронте ударной волны. Результаты расчетов хорошо согласуются с данными из классических источников [6; 7].

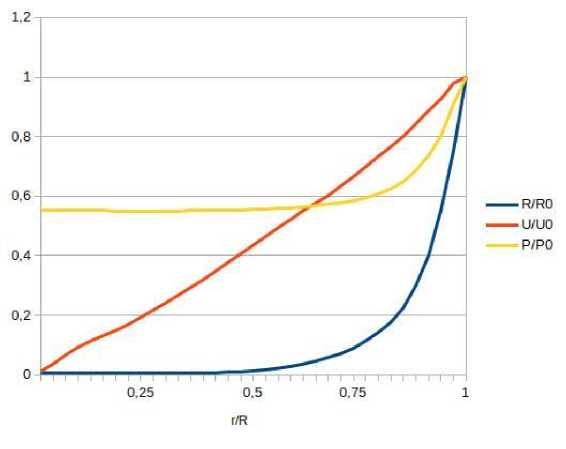
Рис. 1. Распределения плотности, скорости и давления, нормированные относительно значений на фронте ударной волны.